图机器学习【从理论到实战】

---

1、图机器学习导论

1.1图神经网络与普通神经网络的异同

传统神经网络
以往：随着机器学习、深度学习的发展，语音、图像、自然语言处理逐渐取得了很大的突破，然而语音、图像、文本都是很简单的序列或者网格数据，是很结构化的数据，深度学习很善于处理该种类型的数据。

---

图神经网络
现实世界：并不是所有的事物都可以表示成一个序列或者一个网格，例如社交网络、知识图谱、复杂的文件系统等，也就是说很多事物都是非结构化的。

---

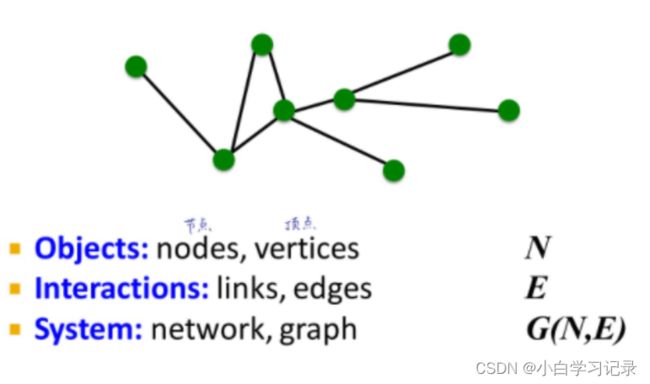
2、图的基本表示和特征工程

2.1 图的基本表示

内容：
图的本体设计
图的种类（有向、无向、异质、二分、连接带权重）
节点连接数
图的基本表示-邻接矩阵
图的基本表示-连接列表和邻接列表
图的联通性

---

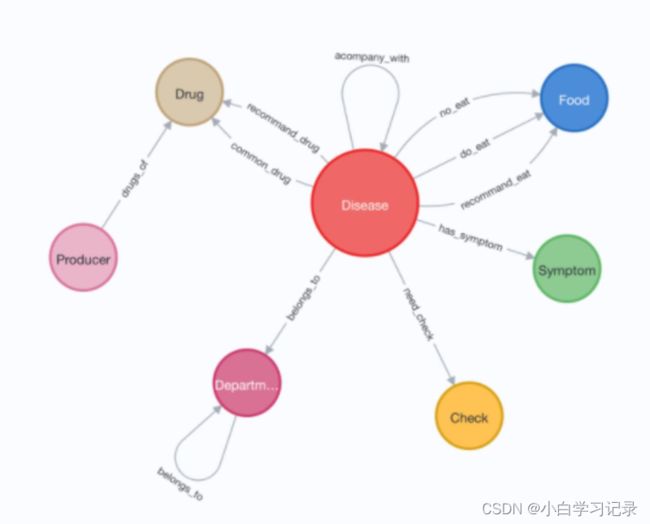
2.1.1 图的本体设计

• 如何设计图的本体设计取决于将来想解决什么问题。
• 从中心点出发，将所需要的要素根据中心点延伸。来判断节点种类和个数
  

---

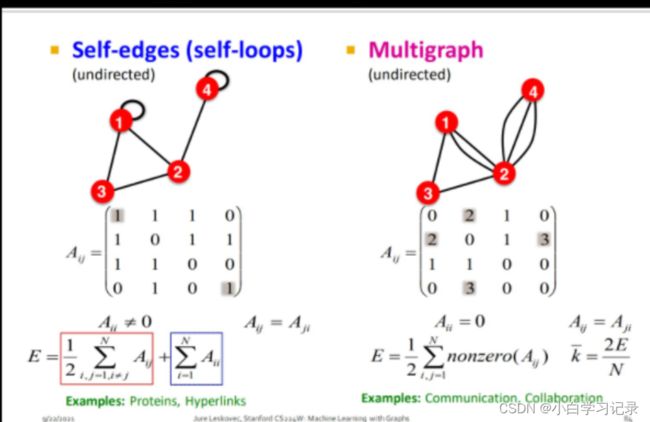
2.1.2 图的种类

图的种类：（有向、无向、异质、二分、连接带权重）

---

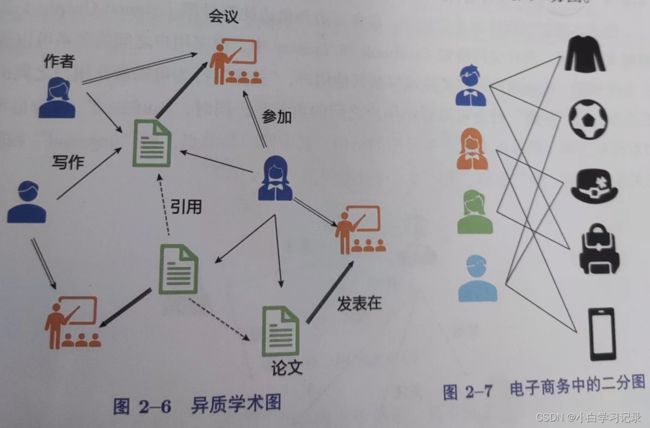
异质图

同质图：只包含一类型节点和一类型边
一个异质图G由一组节点V和一组边E构成。其中每个节点和每条边都对应着一种类型.T就是表示节点类型集合，R表示边类型集合。

二分图：G={V,E}
节点集V可以分为两种不相交的子集V1,V2。而E中的每条边都连接着V1中的一个节点和V2中的一个节点。二分图广泛用于捕获不同对象之间的互动。

---

二分图展开

---

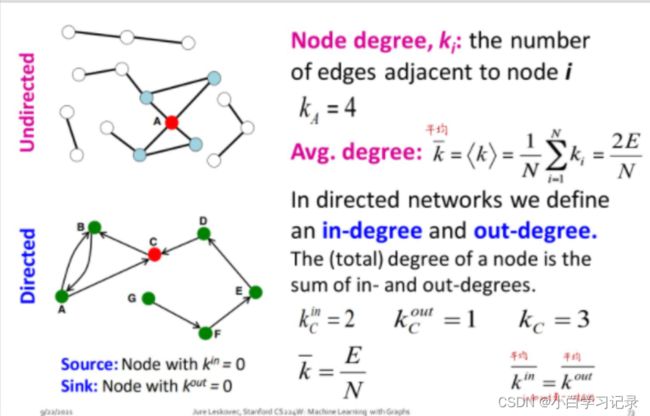
2.1.3节点连接数（度）

度：表示这个节点和其他相邻节点的次数

---

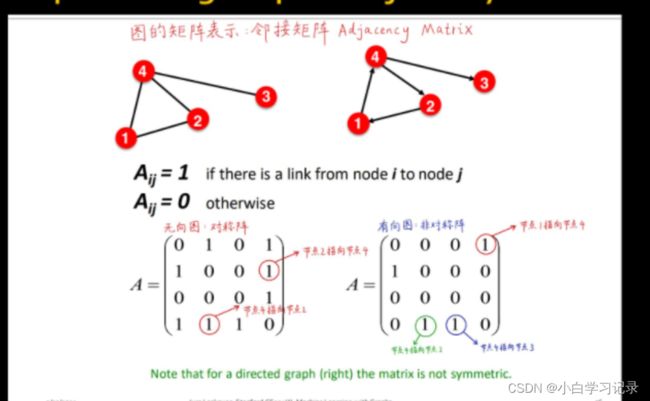
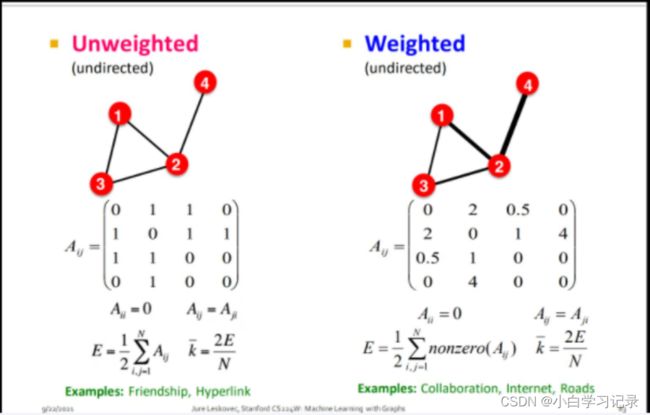
2.1.4图的基本表示（邻接矩阵）节点数量少使用

---

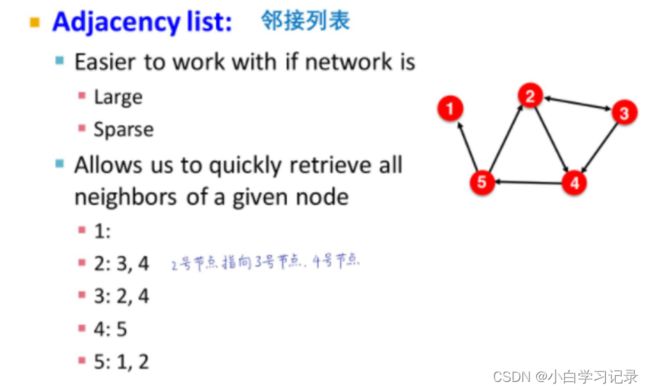
2.1.5图的基本表示（连接列表和邻接列表）数量巨大采用

只记录存在连接的节点对

---

只记录存在关系的节点对，每个节点依次排开，只记录与它有关系的节点

---

带权重的图

---

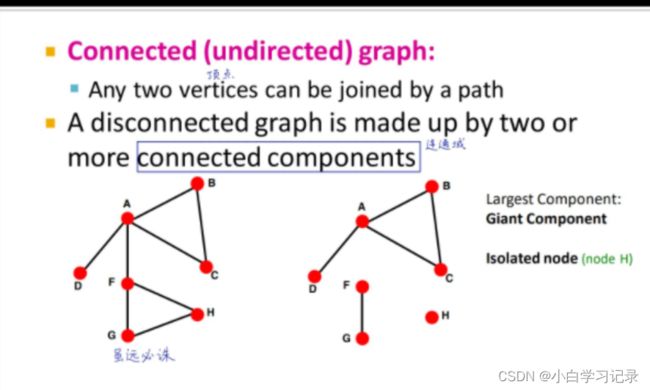
2.1.6图的连通性

• 如果一个图任意两节点间，总有一条路可以触达，称为连通图
• 否则称为非连通图，由多个连通域组成

---

2.2传统机器学习和特征工程

2.2.1 传统机器学习

这里的features包括两种类型：结构(structural)特征、描述节点的属性(attribute)和properities特征

人工特征工程+机器学习

• 图机器学习的基本任务：
• 节点层面：信用卡欺诈
• 连接层面：可能认识的人
• 子图/全图层面：用户聚类、分子是否消毒
  
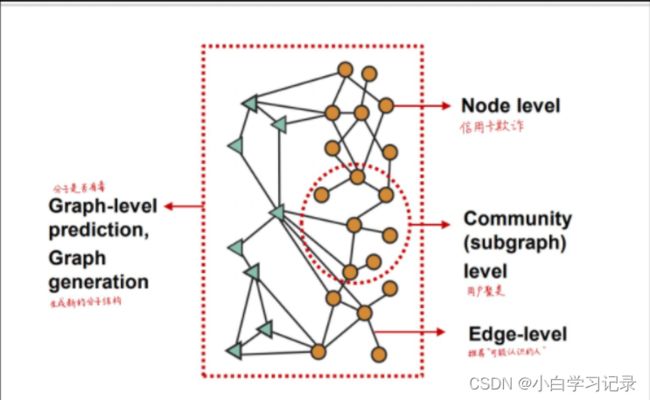
  Traditional ML Pipeline：首先获取nodes、links、graph的特征向量；然后训练一个ML model;最后在新的数据上(新的node link graph的特征向量)应用model，做出预测。Traditional ML Pipeline使用手工设计的特征。

2.2.2 节点层面的特征工程

通过已知节点补全未知节点

目标：构造网络中的特征以及节点的位置

• 节点连接数
• 节点中心性
• 集群系数
• 子图模式

A.节点连接数

节点v的度数$k_v$是节点v的邻居节点数(与v相连的边数)
缺陷：将所有邻居节点同等对待，无法捕捉邻居节点的重要性。(如果几个节点的度数相同，则特征向量相同，则模型对它们做出的预测相同。没办法区分它们)

B.节点中心性即考虑图中节点的重要性

• Eigenvector centrality
• 如果节点v被重要的nodes包围$u\in N(v)$，则节点v是重要的(我的邻居都重要，那我应该也重要)。
  由于左式是递归的，我们如何求解呢？
  $c_{max}$对应着${\lambda }_{max}$，即最大特征值对应的特征向量，${\lambda }_{max}$总是正值且是唯一的

• Betweenness centrality
  如果一个节点在许多其他成对节点的最短路径上，那么节点重要。（如果一个节点是重要的连接器交通枢纽，那很重要）
  
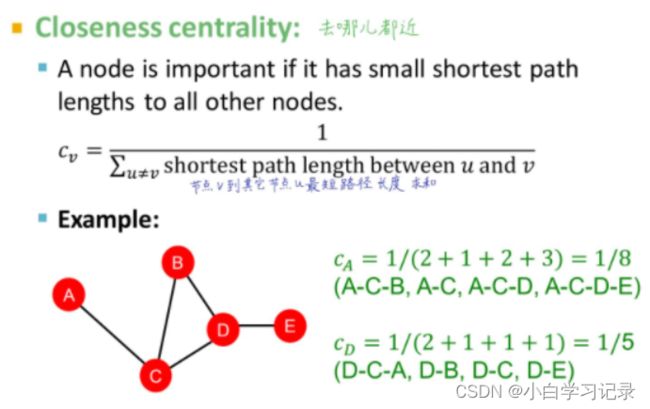
• Closeness centrality
  值越大越好
  如果一个节点有到所有其他节点的最短路径，那么这个节点是重要的。
  

C. Clustering coefficient

• 聚类系数用来评价节点周围邻居节点的连接程度
• $e_v$=邻居节点真实存在边数➗最多可能存在边数
  
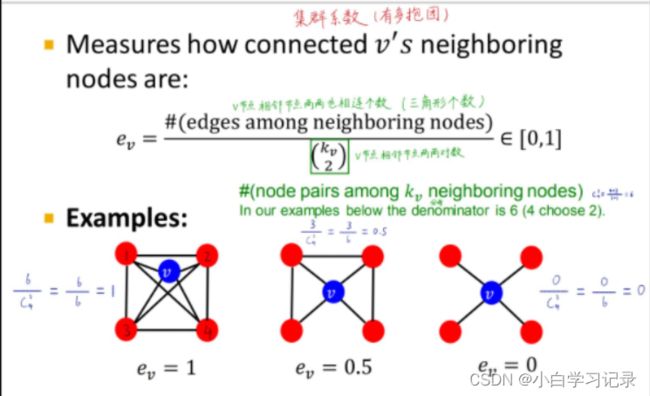
  观察到聚类系数计算的是ego-network中三角形的数量(在社交网络中我的朋友的朋友也可能是我的朋友，社交网络会随着三角形的闭合而发展)

D.graphlet Degree Vector(GDV)——是一个根植于给定节点的子图的数量向量

那能否对三角形进行扩展，一般化为计算给定节点附近预先指定的子图的数量——graphlets，将仅仅对三角形的计数扩展到任意结构的子图。
graphlets：rooted(基于给定节点)连通的异构子图与motifs区分

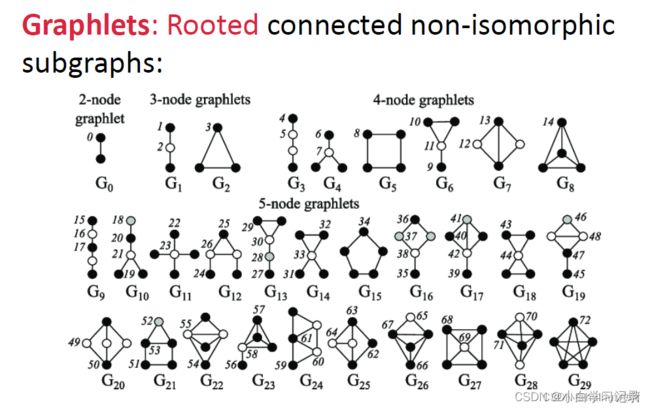
因为graphlets是诱导子图( induced subgraph 节点的所有连接都要包含在内)，所以节点在位置c不行，另两个节点必须要连接。

GDV提供了一种测量节点局部网络拓扑的方法，通过比较两个节点的GDV提供了一种比node degree和聚类系数更细节的测量局部拓扑相似性的方法。

总结

node features可以分为:

1. Importance-based features：捕获节点在图中的重要性
   node degree：只计算了节点邻居节点的数量
   Node centrality：可以区别对待邻居节点Models importance of neighboring nodes

2. Structure-based features：捕获节点局部邻域的拓扑结构
   node degree：只计算了节点邻居节点的数量
   聚类系数：用来评价节点周围邻居节点的连接程度
   GDV：计数不同的graphlets的数量

2.2.3 连接层面的特征工程

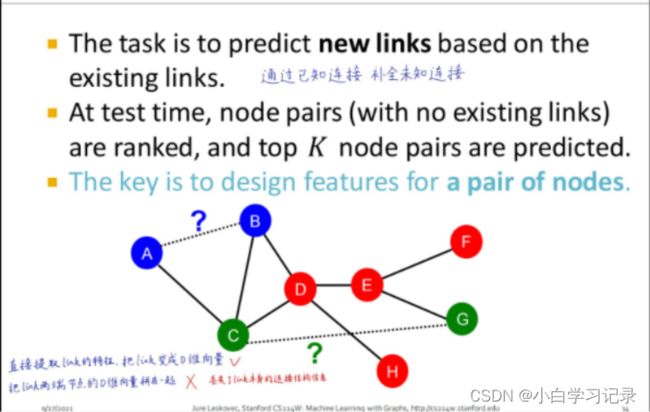
通过已知连接补全未知连接

A.链路级预测任务:Recap

• 任务:根据现有的链接预测新的链接。测试时，对无链路的节点对进行排序，预测top k节点对。关键是为一对节点设计特征。
  

• 链接预测任务的两种公式:

• 随机缺失边
  移除一组随机的链接，然后目标是预测它们的连接情况。类似于化学键研究，不同的化学键的功能不一样。

• 随时间演化边
  现在有一个按照时间${t_0}^{\prime }$时候的边来定义的图 $G[t_0,{t_0}^{\prime }]$，输出一个排序后的边列表，这里的边不是之前${t_0}^{\prime }$时候的边，而是按照时间预测出来的 $G[t_1,{t_1}^{\prime }]$。这个类似于人随着时间发展扩展自己的朋友圈。采用的评价方式是$[t_1,{t_1}^{\prime }]$时间段内产生的新边期望和取L的最上面n个元素，并计算正确的边数。
  

B.链接预测

a.基于两节点距离：

两点间最短路径的长度 distance-based feature：

缺点：这种方式的问题在于没有考虑两个点邻居的重合度（the degree of neighborhood overlap），如B-H有2个共同邻居，B-E和A-B都只有1个共同邻居。

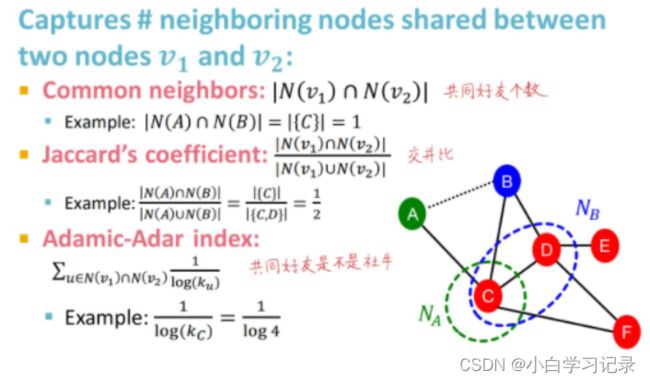
b.基于两节点局部连接信息：

捕获两个节点和之间共享的相邻节点:

1. 共同的邻居: $N(v_1)\bigcap N(v_2)$
   例如：$|N(A)\bigcap N(B)|=|C|=1$
2. Jaccard的系数：$$\frac{N(v_1)\bigcap N(v_2)}{N(v_1)\bigcup N(v_2)}=\frac{N(v_1)\bigcap N(v_2)}{N(v_1)\bigcup N(v_2)}=\frac{|C|}{|C,D|}=\frac{1}{2}$$
3. Adamic-Adar指数:$$\sum _{u\in N(v_1)\bigcap N(v_2)}\frac{1}{log(k_u)}$$
   例如：$$\frac{1}{log(k_c)}=\frac{1}{4}$$
   共同的邻居的问题在于度数高的点对就会有更高的结果，Jaccard的系数是其归一化后的结果。Adamic-Adar指数在实践中表现得好。在社交网络上表现好的原因：有一堆度数低的共同好友比有一堆名人共同好友的得分更高。

c.基于两节点在全图的连接信息：

local neighborhood overlap的限制在于，如果两个点没有共同邻居，值就为0。

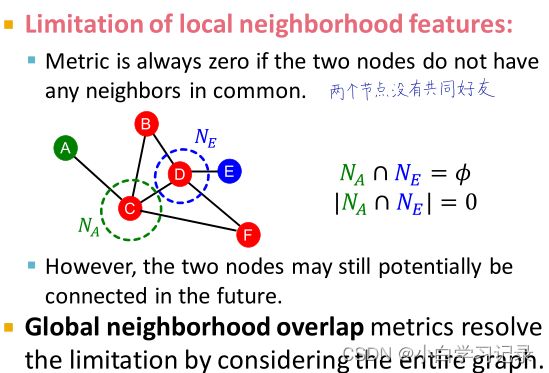
• 但是这两个点未来仍有可能被连接起来。所以我们使用考虑全图的global neighborhood overlap来解决这一问题，主要计算Katz index。
  Katz index：计算点对之间所有长度路径的条数
  计算方式：邻接矩阵求幂
  邻接矩阵的k次幂结果，每个元素就是对应点对之间长度为k的路径的条数
  证明如下：

显然 ${\mathbf{A}}_{uv}$ 代表u和v之间长度为1的路径的数量。上图计算了${\mathbf{P}}^{(1)}$，接下来要计算${\mathbf{P}}^{(2)}$，具体方法如下：

如图所示，计算u和v之间长度为2的路径数量，就是计算每个u 的邻${\mathbf{A}}_{ui}$（与u有长度为1的路径）与v之间长度为1的路径数量${\mathbf{P}}_{iv}^{(1)}$ 即${\mathbf{A}}_{iv}$的总和${\sum }_i{\mathbf{A}}_{ui}\ast {\mathbf{A}}_{iv}={\mathbf{A}}_{uv}^2$
同理，更高的幂（更远的距离）就重复过程，继续乘起来。
从而得到Katz index的计算方式：

总结：

• 两点间最短路径的长度 distance-based feature:
  使用两个节点之间的最短路径长度，但没有捕捉到邻域如何重叠。
• 捕获节点的共同邻居数 local neighborhood overlap:
  捕获两个节点共享的相邻节点的数量。当没有邻居节点被共享时，值为0。
• 全域邻居节点重叠 global neighborhood overlap:
  采用全局图结构对两个节点进行评分。Katz索引计数两个节点之间的所有长度的散步数。

2.2.4 全图层面的特征工程

图级别特征构建目标：找到能够描述全图结构的特征。

2.2.4.1背景知识：Kernel Methods

类似于SVM的核函数，定义好以后，通过核函数矩阵的映射，就可以按照之前的方式来处理了。

2.2.4.2 概述

图核:度量两个图之间的相似性:

• Graphlet Kernel
• Weisfeiler-Lehman Kernel
• 目标：接下来就把之前的“找到能够描述全图结构的特征”转换成只需要找到“图特征向量$\varphi (G)$

2.2.4.3 Graph kernel：Key Idea

回想之前NLP领域应用最多的词袋模型（Bag-of-Words (BoW)），它是将单词计数作为文档的特性(不考虑排序)。
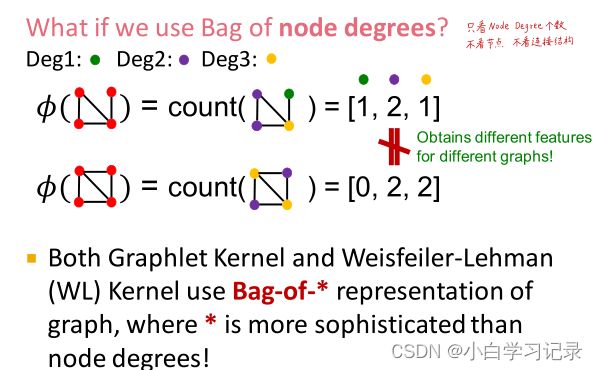
这里我们把图看作一个向量，图中节点看作是单词。

如上图所示，光用node不够的话，可以设置一个degree kernel，用bag-of-degrees来描述图特征。

2.2.4.4 Graphlet Feature

Key idea： 计算图表中不同的graphlets的数量这里graphlet的定义与节点级特性略有不同，俩处不同在于：

1. 这里的graphlet中的节点不需要连接(允许独立的节点)
2. 这里的graphlet没有根

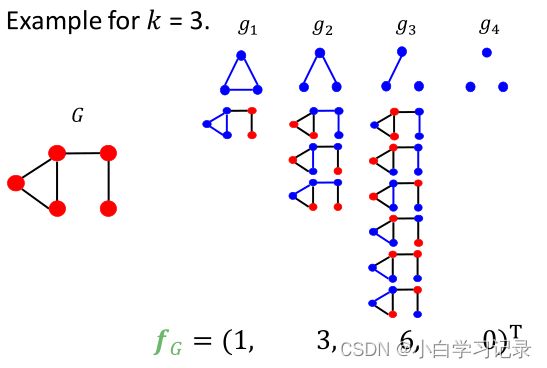
A 对每一种节点数，可选的graphlet：

B graphlet count vector：每个元素是图中对应graphlet的数量：

C graphlet kernel：

graphlet kernel就是直接点积两个图的graphlet count vector得到相似性。对于图尺寸相差较大的情况需进行归一化

graphlet kernel的限制：计算昂贵，原因如下：

接下来，就是对刚才graphlet核方法的改进。

2.2.4.5 Weisfeiler-Lehman kernel：

相比graphlet kernel代价较小，效率更高。用节点邻居结构迭代地来扩充节点信息。
广义的节点度袋，因为节点度是单跳邻域信息。

color refinement示例
把邻居颜色聚集起来

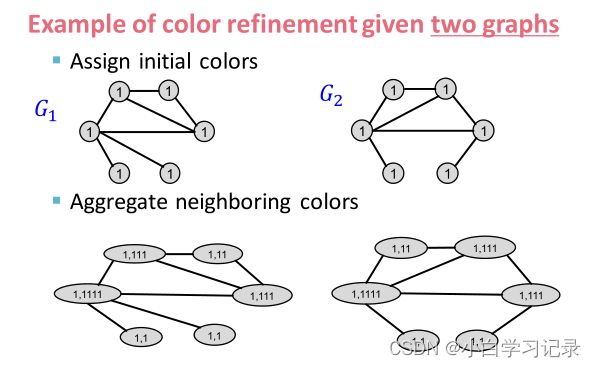
对聚集后颜色取哈希值

把hash后的颜色聚集起来

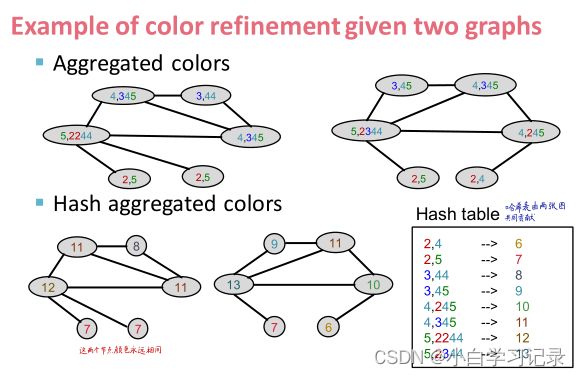
进行K次迭代12后，用整个迭代过程中颜色出现的次数作为Weisfeiler-Lehman graph feature

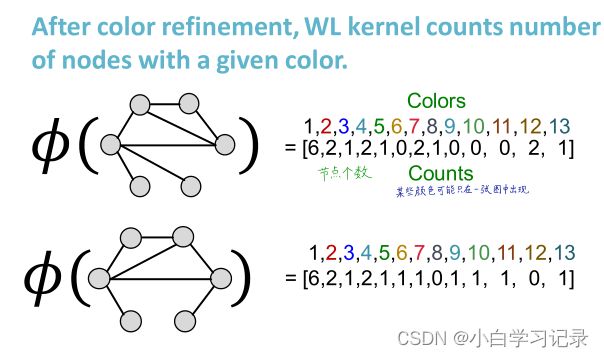
通过颜色计数向量的内积计算WL核值

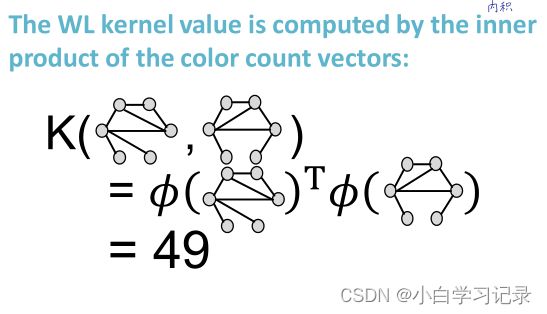
WL kernel的优势在于计算成本低

2.2.4.6 总结

Graphlet Kernel

• Graph表示为Bag-of-graphlets
• 计算量大

Weisfeiler-Lehman Kernel

• 应用-步色彩细化算法丰富节点色彩
  不同的颜色捕捉不同的-hop社区结构
• 图用颜色袋表示
• 计算效率
• 与图神经网络密切相关(我们将看到!)

3、图机器学习代码实战

3.1、networkx基本说明

# 导入工具包
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签 
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号

# 1.全连接无向图
G=nx.complete_graph(6)
nx.draw(G)
# 判断是否是有向图
print(G.is_directed())
# 全图连接数
G.size()

# 2.全连接有向图
J=nx.complete_graph(6,nx.DiGraph())
nx.draw(J)
# 判断是否是有向图
print(J.is_directed())
# 全图连接数
J.size()

# 1.导入 csv 文件定义的三元组连接表，构建有向图
import pandas as pd
df = pd.read_csv('./【A】networkx基本说明/【A3】创建图-连接表和邻接表创建图/triples.csv')
# print(df)
# 2.通过连接表Edge List创建图
G = nx.DiGraph()
edges = [edge for edge in zip(df['head'], df['tail'])]  #生成节点列表
G.add_edges_from(edges)  # 添加节点
# print(G.edges('关羽')) #查看节点参数
# 3.可视化
pos = nx.spring_layout(G, seed=123) # 节点排版布局-默认弹簧布局，随机数种子
plt.figure(figsize=(10,10))
nx.draw(G, pos=pos, with_labels=True)
# 4.查看全图参数
print(G)
len(G)
G.size()
G.nodes
# 5.保存并载入邻接表Adjacency List
for line in nx.generate_adjlist(G):
    print(line)
# 将邻接表导出为本地文件 grid.edgelist
nx.write_edgelist(G, path="grid.edgelist", delimiter=":")
# 从本地文件 grid.edgelist 读取邻接表
H = nx.read_edgelist(path="grid.edgelist", delimiter=":")
# 可视化
plt.figure(figsize=(10,10))
pos = nx.spring_layout(H, iterations=3, seed=123)
nx.draw(H, pos, with_labels=True)
plt.show()

# 1.创建无节点、无连接的空图
G = nx.Graph()
G.nodes
# 2.添加单个节点
G.add_node('刘备')
# 3.添加多个节点
G.add_nodes_from(['诸葛亮', '曹操'])
G.add_nodes_from(range(100, 105))
# 4.添加带属性特征的节点
G.add_nodes_from([
    ('关羽',{'武器': '青龙偃月刀','武力值':90,'智力值':80}),
    ('张飞',{'武器': '丈八蛇矛','武力值':85,'智力值':75}),
    ('吕布',{'武器':'方天画戟','武力值':100,'智力值':70})
])
print(G.nodes) #节点数
# 可视化
# nx.draw(G)
# 5.将H的节点添加到G中
## 创建另一个首尾相连成串的线性串珠图
H = nx.path_graph(10)
G.add_nodes_from(H) # 将H的节点添加到G中
print(G.nodes) #节点数
# 可视化
nx.draw(G)

# 创建单个连接，设置属性特征
G.add_edge(0, 1, weight=0.5, like=3) # 特征属性的名字可以随便起
# 创建多个连接
G.add_edges_from([
  (1,2, {'weight': 0.3, 'like':5}),
  (2, 0, {'weight': 0.1, 'like':8})
])
#
G.edges[(0, 1)]   # 查看连接属性,edges-连接
# 全图连接信息
print(G.number_of_edges())
G.size()
# G.edges()
G.edges(data=True) # 带属性的连接
# 遍历所有连接，data=True 表示输出连接特征属性信息
for edge in G.edges(data=True):
    print(edge)
# 指定节点
node_id = 1
G.degree[node_id] # 节点连接数
# 指定节点的所有相邻节点
for neighbor in G.neighbors(node_id):
    print("Node {} has neighbor {}".format(node_id, neighbor))

3.2、nx.draw可视化

# 导入工具包
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 规范中文格式
plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签  
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
# 创建4x4网格图
G = nx.grid_2d_graph(4, 4)
pos = nx.spring_layout(G, seed=123)
plt.figure(figsize=(4,4))
nx.draw(G, pos, with_labels=True)
# 不显示节点
plt.figure(figsize=(4,4))
nx.draw(G, pos, node_size=0, with_labels=False)
# 设置颜色
len(G.edges())  #边的长度
plt.figure(figsize=(4,4))
nx.draw(
    G,
    pos,
    node_color='#A0CBE2',      # 节点颜色
    edgecolors='red',          # 节点外边缘的颜色
    edge_color="blue",         # edge的颜色
    # edge_cmap=plt.cm.coolwarm, # 配色方案
    node_size=800,
    with_labels=False,
    width=3,
)
# 有向图
plt.figure(figsize=(4,4))
nx.draw(
    G.to_directed(),
    pos,
    node_color="tab:orange",
    edgecolors="tab:gray",
    node_size=400,
    with_labels=False,
    arrowsize=10,
    width=2,
)

4、图嵌入表示学习

4.1、Traditional ML for Graphs的流程

• 给定一个图，提取features(node edge graph-level features)，然后学习一个模型，最终将这个模型用于预测。

• 抽取d个特征，编码为D维向量。

• 特征自带属性和结构信息；本教程只讲连接特征，不讲属性特征，所以特征工程的目标基本是如何把节点映射为D维向量？
  

• 时间大多花费在特征工程中(为了能找到最好描述网络的特征，最后将特征用在下流预测任务)。

4.2、Graph Representation Learning（图表示学习）

• 可以自动学习特征，减轻每次都要手动提取特征(特征工程)的需要。
  
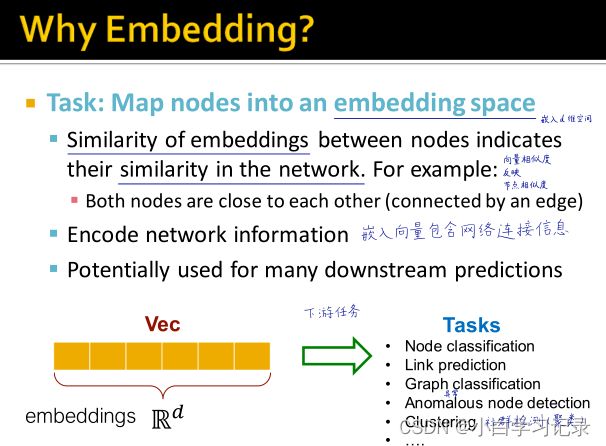
• 目标：通过图机器学习，高效学习与下游任务无关的特征。
• 例如：在节点水平,学习如何在d维空间上映射此节点，将d维的向量称为特征表示(或embedding)。mapping过程自动发生，且d维向量捕获我们感兴趣的网络的底层拓扑结构。
  

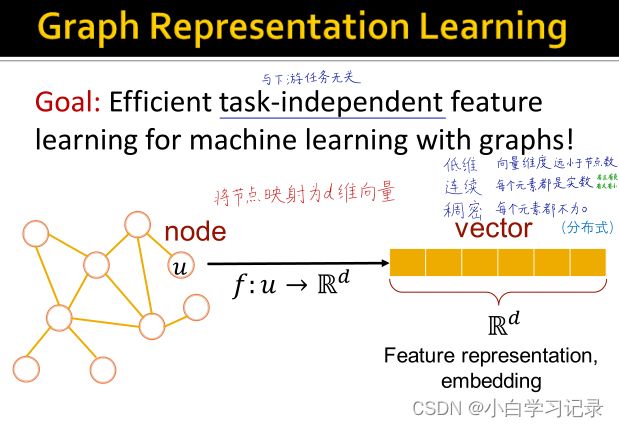
4.3、为什么要嵌入？（why embedding?）

• 任务：将节点映射到embedding space
• 向量相似性可以表示它们节点相似性。
• 嵌入向量包含网络连接信息。
• 可以用于不同的下游预测任务。
  
• 节点嵌入的例子：原图中相近的节点嵌入后仍然相近。
  

4.4、图嵌入-基本框架（编码器–解码器）

• 定义节点集
  

• 定义节点相似度
  

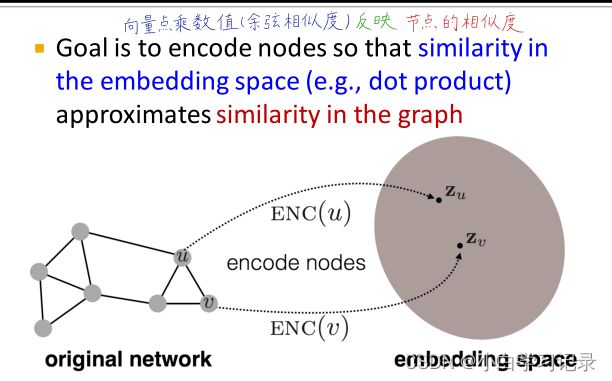
• 对节点进行encoder(映射到embedding 空间)，因此在embedding空间中的相似性近似于原始图中的相似性。学习这个encoder

• 向量点乘数值（余弦相似度）反映节点相似度。
  
  

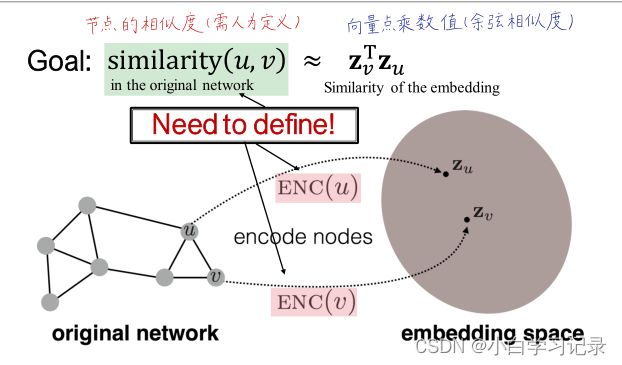
4.4.1、具体流程:

1. 定义节点集
2. 定义一个相似性函数(一种原始网络的相似性度量)
3. Decoder将embeddings映射到similarity score(这里使用了最简单的decoder，点积)
4. 优化encoder的参数，使得$similarity(u,v)\approx z_v^T{z}_u$

---

4.4.2、两个关键点：

4.4.3、“shallow”embedding

比较简单的Encoder只是一个embeddiing-lookup(查找表)。只要找到一个embeddings的矩阵，就只需要查找对应编号的节点的embedding。Z是d×|V|维的矩阵，第i列为节点i的embedding。v是位置向量(indicator)，是one-hot编码，除了表明是节点v的元素为1，其它元素都为0.

每一个节点被分配一个独一无二的embedding 向量，我们直接优化每一个每一个节点的embedding。

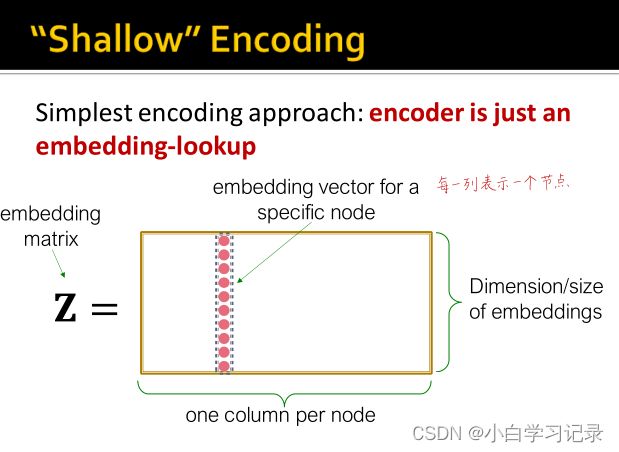
4.4.4、框架总结 Encoder+Decoder FrameWork

• hallow encoder：仅是简单的embedding查找表
• 优化参数：对于简单的encoder，优化的是Z中每一个节点的embedding

当然之后也会介绍deep encoder

• Decoder：基于节点相似性，此处仅是简单点积
• Objective：最大化相似的节点对(u,v)的$z_v^T{z}_u$
  

4.4.5、Note on Node Embeddings

学习节点嵌入是unsupervised/self-supervised的方式，因为：

• 没有使用节点标签
• 没有使用节点features(一些额外的属性信息)
• 目的是直接估计一个节点的坐标(embedding)，因此可以保留一些网络结构方面的知识( DEC捕获)。
• 这些embeddings和任务是独立的task independent。并没有经过特定任务的训练，仅是经过网络本身训练，可以用于任何task。

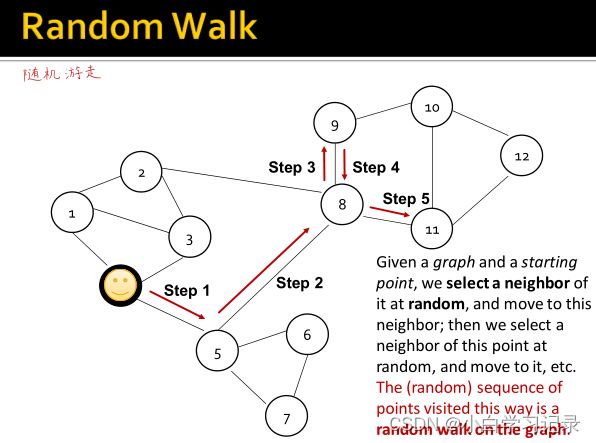
4.5、随机游走

4.5.1 定义

4.5.2 随机游走的计算方法

• 从u点出发的随机游走序列经过v节点的概率
• 节点“相似”定义：共同出现在同一个随机游走序列。
  
• 采样得到若干随机游走序列，计算条件概率
• 迭代优化每个节点的D维向量，使得序列中共现向量数量积大，不共现节点向量数量积小。
  

4.5.3 为什么选择随机游走？

4.5.4 优化特征学习（feature learning as optimization）

• 最小化损失函数
  
• 为解决softmax难算的问题，提出负采样。
  

4.5.5 同类改进-node2vec:Biased walks

使用灵活的，有偏向的random walks可以平衡网络的局部全局视角，使用BFS搜索(局部)DFS搜索(全局)搜寻节点u的邻居$N_R(u)$。

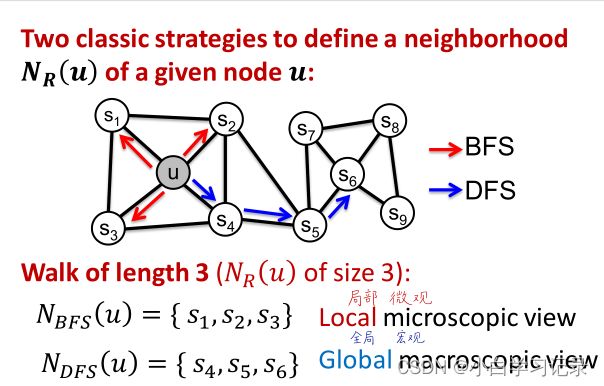
​​​​​​​有两个超参数p和q：p是返回上一个节点，q是走开远离参数。1代表和上一个节点同一水平。

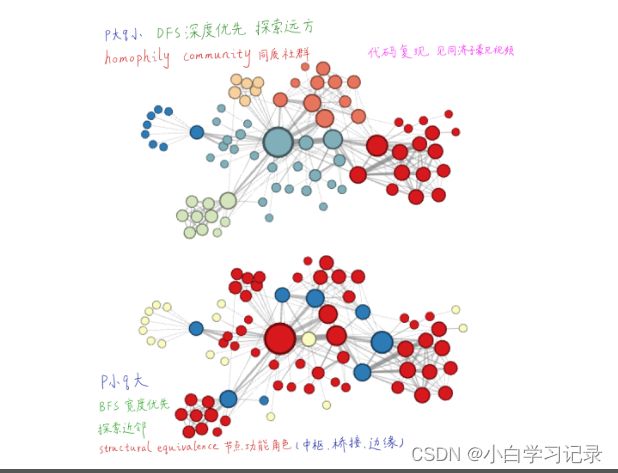
4.5.6 随机游走的缺点

• 无法立刻泛化带新加入的节点，导致测试集可能存在某种程度上的过拟合
• 只能处理结构上相似，地理上相近的节点
• 仅利用图本身的连接信息，没有用对应的属性信息

5、PageRank

Link Analysis approaches—计算图中节点重要性
以网页为例，节点是web pages 边是超链接，仅考虑早期导航类型的超链接，不考虑现在事务性的超链接(发布评论、购买)。web是有向边。

web pages的重要性并不相同，利用web graph的链接结构为pages的重要性排序。

• 如果pages有更多in-coming links，则page更重要—仅计数
• 来自更重要的page的链接更加重要，我的邻居重要我也重要—递归问题

5.1 PageRank—“Flow” Model

基本思路
一个页面很重要：如果他被其他重要的pages指向。

• 每个链接的投票与其源页面的重要性成正比
• 如果具有重要性的页面 i 具有 di 个连出链接，则每个链接都会获得 ri / di 投票
• 页面j本身的重要性rj是其连入链接的投票总和

rj 是节点j的importance score

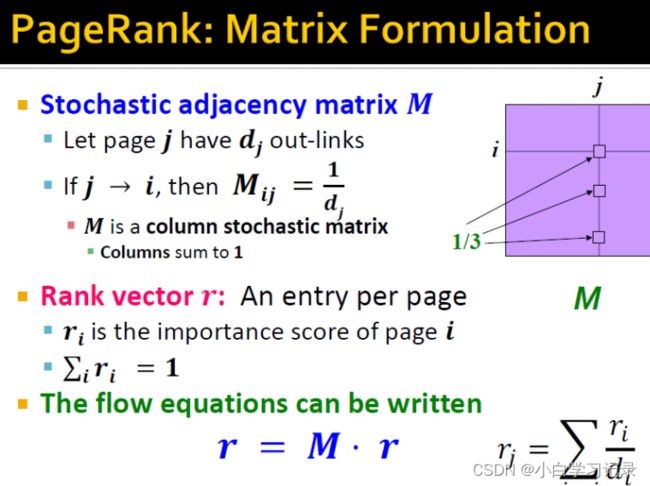
5.2 随机邻接矩阵M

利用M计算上述的Flow equation(如果利用Gaussian elimination则太复杂)

M的限制条件 :M的每列和要为1。

flow equation可以写为：$r=M\ast r$

5.3 M和Random Walk联系起来

r是random walk的一个稳定分布(经过多次迭代)

5.4 M和eigenvector centrality的联系

rank vector(重要性得分)r 是随机邻接矩阵M特征值为1的特征向量

5.5 总结

PageRank:

• 使用 Web 的链接结构测量图中节点的重要性
• 使用随即邻接矩阵M模拟 random web surfer
• PageRank 的解r = Mr 其中r可以看做M的特征值为0的特征向量或者图上random walk的稳定分布

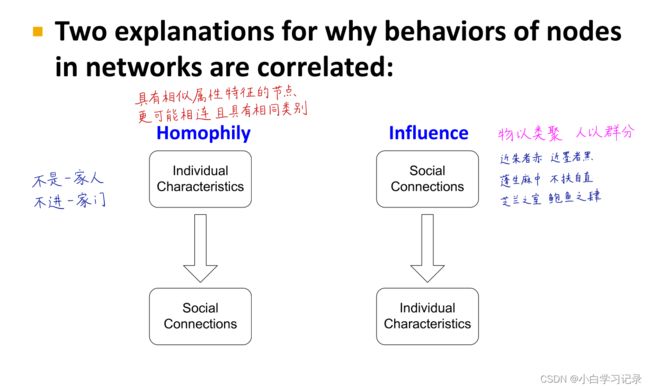
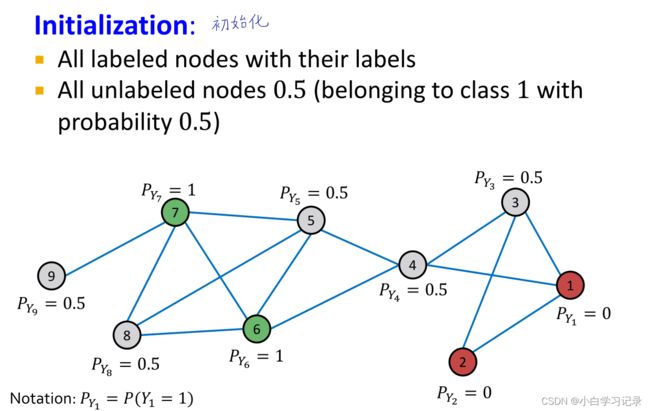
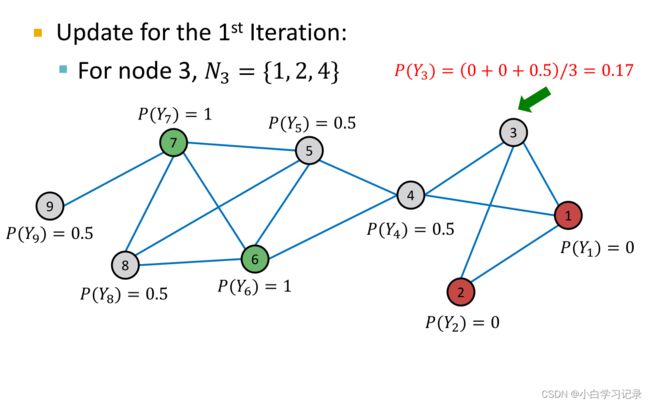
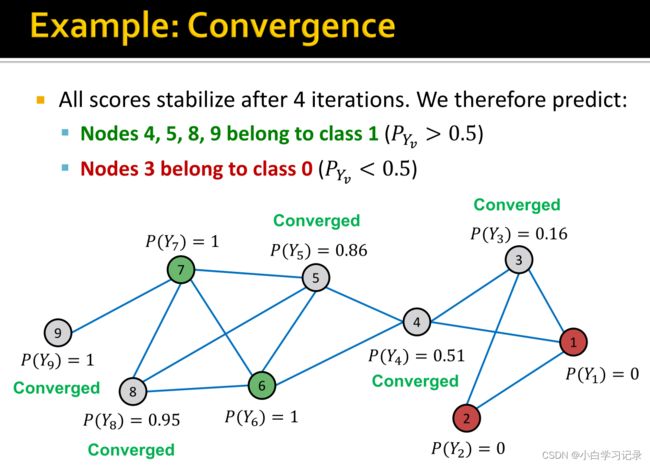
6、半监督节点分类 Label Propagation

• 用已知类别的节点，预测未知类别的节点
  
• 任务目标：
  
• 物以类聚，人以群分
  
• 利用相关连接预测节点标签

• 初始化
  
• 更新节点3

• 多次迭代，收敛

• 挑战