约束满足问题（CSP）

文章目录

前言

一、CSP是什么？

二、约束传播

1.结点相容

2.弧相容

3.路径相容

4.全局约束

三、回溯搜索

1.定义

2.变量和取值顺序

3.智能回溯：向后看

四、局部搜索

---

前言

约束满足问题在人工智能领域有着广泛的应用。比如新的学期教室的规划分配，数独的解，它们都涉及了约束条件。我们所熟知的经典的皇后问题、SAT问题都属于约束满足问题。约束满足问题可以分为二元约束满足问题和多元约束满足问题。其中，多元约束满足问题可以被划分为等价的二元约束满足问题。因而，研究二元约束满足问题是一个重要的研究方向。

---

 

一、CSP是什么？

1.通俗的解释是：一组变量，每个变量有自己的值域。当每个变量都有自己的赋值同时满足所有关于变量的约束时，问题就得到了解决。这类问题就叫做约束满足问题（CSP），全称Constraint Satisfaction Problem。简单理解就是给你几个约束条件，然后给你几个方程组，给我在条件下求出满足方程组的解。

约束满足问题包含三个主要的成分X，D和C：

• X是变量集合 {X1,X2,X3,.....}
• D是值域集合，即每个变量的取值范围。 {D1,D2,D3,....}
• C是描述变量取值的约束集合。

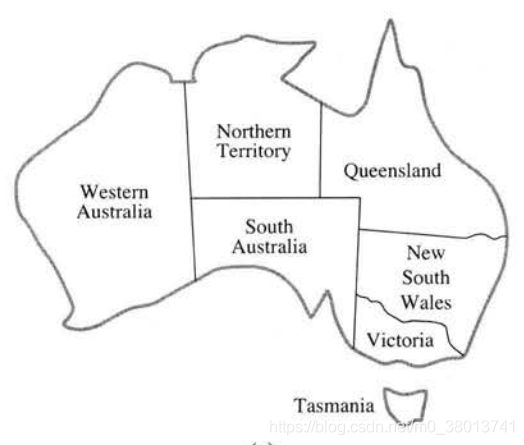
2.举个简单的例子-----地图着色问题：我们的要求是给定三种颜色，对地图进行涂色，要求相邻区域要染成不同的颜色。让我们来转换成上面的定义形式.

• 变量集合X = {Western Australia ，Northern Territory ，South Australia ，Queensland，New South Wales，Victoria}
• 值域集合D = {red，green，blue} 
• 约束集合C = {要求邻域不能是相同颜色}         

 

3.或许会有人问，为啥要把问题形式化成CSP呢？

第一个原因是用CSP表示各种问题会很自然，如果你有一个CSP求解系统，使用它求解问题，比其他搜索方法求解要简单的多。

第二个也是最重要的原因是CSP求解能快速消除庞大的搜索空间。举个例子：

利用约束传播，可以在赋值过程中逐步减少其他未赋值邻域的值域空间，比如上面那个图，Western Australia = 红 ，那么Northern Territory 和 South Australia 的值域中红色就可以去掉了。

 

二、约束传播

在常规的状态空间搜索中，算法只能做一件事：搜索。在CSP中则有了选择，算法还可以做一种称为约束传播的特殊推理：使用约束来减少一个变量的合法取值范围，从而影响到跟此变量有约束关系的另一个变量的取值，如此进行。

核心思想是：局部相容性，具体的种类有如下几种。

 

1.结点相容

如果单个变量（对应于CSP网络中的结点）值域中的所有取值满足它的一元约束，就称此变量是结点相容的的。

举个例子：

            一个人有 {苹果，橘子，香蕉，西瓜}，但是他不喜欢橘子，所以我们把橘子拿走，那剩下的水果就符合了他的条件，即为结点相容的。

 

通过运行结点相容总能消除CSP中的所有一元约束。可以将所有n元约束转换成二元约束。

因为结点约束要求把值域中不满足的值删除，所以在运行结点约束后，CSP中就不存在一元约束了。

 

2.弧相容

如果CSP中某个变量值域中的所有取值满足该变量的所有二元约束，则称此变量是弧相容的。简单来说就是图中两个有弧连接的结点，它们各自的取值要满足它们两个之间的二元约束关系。

举个例子：

   y = 2x

（1，2），（2，4），（3，6），（4，8）

   y的值域应该是{2，4，6，8}

   x的值域应该是{1，2，3，4}

弧相容算法：AC-3

具体的操作过程：为了使每个变量都是弧相容，AC-3算法维护一个弧相容的队列。

（1）首先队列中包含CSP中所有的弧，AC-3从队列中弹出弧（X1,X2）

（2）要求 X1对X2 弧相容（意思是X1的取值得出的结果要属于X2的值域）

（3）如果D没有发生变化（意思是X1中的所有值都满足X2，但也有可能存在不满足的，比如上面的例子中X=5，y中没有10，就要去掉，那么D就发生了变化），算法则处理下一条弧

（4）如果D发生了变化，那么每个指向X1的弧（Xk，X1）都必须重新插入队列中准备检验。之所以这么做是因为D的改变可能引起Dk的缩小。

（5）如果D为空集，则CSP没有解，AC-3返回失败，否则，继续检查。

具体的算法过程如下图所示：

3.路径相容

弧相容通过弧（二元约束）缩紧值域（一元约束）；路径相容通过观察变量得到隐式约束并以此来加强二元约束。

两个变量的集合{X1,X3}对于第三个变量X2是相容的，指的是对{X1,X3}的每一个相容的赋值{X1=a,X3=b}，X2都有合适的取值同时使得{X1,X2},{X2,X3}是相容的。其实简单理解就是  X1-->X2-->X3的传递依赖一样。

 

4.全局约束

简单理解就是在全局对变量进行约束。其实可以理解为全局变量。

Alldiff约束：表示所有相关变量必须取不同的值。

资源约束（atmost约束）：比如调度问题中，用p1,p2,p3,p4表示执行四项任务的人数，要求总人数不超过10人（资源约束）。

 

三、回溯搜索

1.定义

回溯搜索用于深度优先搜索中，它每次为一个变量选择一个赋值，当没有合法的值可以赋给某变量时就回溯。

具体步骤：它不断选择未赋值变量，轮流尝试变量值域中的每一个值，试图找到一个解。一旦检测到不相容，返回上一次条用尝试另一个值，直到找个一个完整解。

回溯算法如下图所示：

举个例子：下面这个图，按照某个要求进行赋值，假设一直沿着1走，当走到第二个1后，发现在约束条件下无法继续赋值，比如说要求两个结点数加起来要满足5，那么就不满足了，就回溯到第一个1，走2这个结点，还不满足，继续回溯，直到走到4，满足了，沿着1-4继续往下走。这个不断更换值去满足条件的过程就是回溯。

2.变量和取值顺序

（1）最少剩余值启发式(MRV),也称为”最受约束变量“ 或 ”失败优先启发式“

         它选择最可能很快导致失败的变量，从而对搜索树进行剪枝。

（2）度启发式

        选择与其他未赋值变量约束最多的变量来试图降低未来的分支因子。

        比如说还是下面这个图，我们先选择SA的赋值，一旦SA的值确定了，那么WA,NT,Q,NSW,V的值域就可以进行删减，缩小它们的值域，进而更快的找到结果。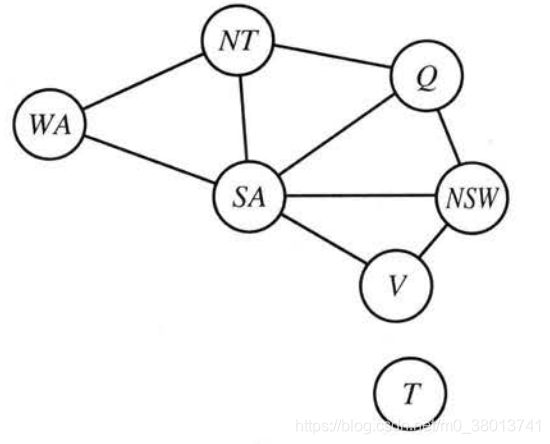

（3）最少约束值

         优先选择的值时给邻居变量留下更多的选择。

总结：MRV和度启发是在回溯搜索中决定下一步选择哪个变量的方法，都独立于领域。最少约束值启发式则是帮助变量选取合适的值。

3.智能回溯：向后看

（1）时序回溯

       退回前一个变量并尝试另一个值

（2）智能回溯  ---  回跳

      退回到可能解决这个问题的变量。也就是说直接回溯到导致问题的根源，有时候也许不止跳跃一步。

 

四、局部搜索

初始状态是给每个变量都赋一个值，搜索过程是一次改变一个变量的取值。

举个例子：八皇后问题，它的问题是这样的，有八个皇后分布在一个8×8的网格上，要求行，列，斜线都只能有一个皇后存在，它们应该分别在什么位置。

初始状态是八个皇后在八列上的一个随机布局，然后每步选择一个皇后进行移动，在这里我们使用最少冲突启发式（选择和其他变量冲突最少的值）来进行解决。

我们使用局部搜索，然后利用最少冲突启发式计算冲突值，选择其中最小的位置，移动一个皇后。比如上面第二个图，（1，6）这个位置从行，列，斜着 数共有三个皇冠，所以它的数值是3，依次计算完成后，我们可以看到（8，6）为0，是最小的，所以位置确定，然后如此直到最后。