循环神经网络（二）（简单循环神经网络，keras 实现）

循环神经网络是一系列神经网络的统称，其主要特点是在序列数据上重复使用相同的结构，对序列数据中的依存关系建模，用于序列数据的预测。简单循环神经网络是最基本的模型，大多数循环神经网络都是其扩展，学习算法是反向传播。

简单循环神经网络

当你在阅读这个句子时，你是一个词一个词地阅读（或者说，眼睛一次扫视一次扫视地阅读），同时会记住之前的内容。这让你能够动态理解这个句子所传达的含义。生物智能以渐进的方式处理信息，同时保存一个关于所处理内容的内部模型，这个模型是根据过去的信息构建的，并随着新信息的进入而不断更新。

循环神经网络（RNN，recurrent neural network）采用同样的原理，不过是一个极其简化的版本：它处理序列的方式是，遍历所有序列元素，并保存一个状态（state），其中包含与已查看内容相关的信息。实际上，RNN 是一类具有内部环的神经网络。

模型定义

考虑序列数据的预测问题。给定输入的实数向量序列 ${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{T}}$；在 $t=1,2,\cdots ,T$ 个位置上，对实数向量 ${\mathbf{x}}_{\mathbf{t}}$ 进行预测，给出概率分布 ${\mathbf{p}}_{\mathbf{t}}$；整体产生输出的概率向量序列 ${\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_{\mathbf{T}}$。

一个朴素的方法是用前馈神经网络完成这个任务。假设序列数据的长度固定，将输入的实数向量序列拼接，作为前馈神经网络的输入，将输出的概率向量拼接，作为前馈神经网络的输出。但序列数据的长度通常是可变的，而前馈神经网络的输入层的宽度是固定的，需要对数据进行截断或补齐处理。此外，序列数据通常在不同位置上有相似的局部特征，而前馈神经网络对不同位置的局部特征是分开表示和学习的，产生冗余，会降低表示和学习的效率。

RNN 的基本想法是，在序列数据的每一个位置上重复使用相同的前馈神经网络，并将相邻位置的神经网络连接起来；用前馈神经网络隐层的输出表示当前位置的状态。下面给出简单循环神经网络的定义。

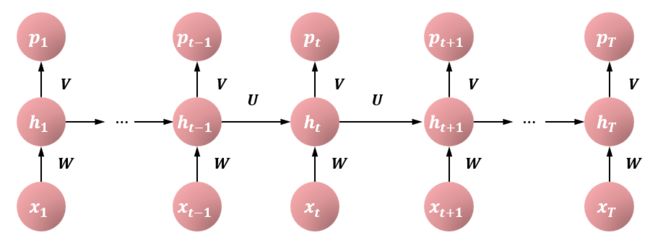
称以下的神经网络为简单循环神经网络。神经网络以序列数据 ${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{T}}$ 为输入，每一项是一个实数向量。在每一个位置上重复使用同一个神经网络结构。在第 $t$ 个位置上，神经网络的隐层或中间层以 ${\mathbf{x}}_{\mathbf{t}}$ 和 ${\mathbf{h}}_{\mathbf{t}-1}$ 为输入，以 ${\mathbf{h}}_{\mathbf{t}}$ 为输出，其间有以下关系成立：$${\mathbf{h}}_{\mathbf{t}}=\text{tanh}(\mathbf{U}\cdot {\mathbf{h}}_{\mathbf{t}-1}+\mathbf{W}\cdot {\mathbf{x}}_{\mathbf{t}}+\mathbf{b})$$ 其中，${\mathbf{h}}_{\mathbf{t}-1}$ 表示第 $t-1$ 个位置的状态，也是一个实数向量；${\mathbf{h}}_{\mathbf{t}}$ 表示第 $t$ 个位置的状态，也是一个实数向量；$\mathbf{U},\mathbf{W}$ 是权重矩阵；$\mathbf{b}$ 是偏置向量。神经网络的输出层以 ${\mathbf{h}}_{\mathbf{t}}$ 为输入，${\mathbf{p}}_{\mathbf{t}}$ 为输出，有以下关系成立：$${\mathbf{p}}_{\mathbf{t}}=\text{softmax}(\mathbf{V}\cdot {\mathbf{h}}_{\mathbf{t}}+\mathbf{c})$$

下图给出简单循环神经网络的架构。可以看作是在序列数据上展开的前馈神经网络，其中参数在各个位置共享。

模型特点

定义中不仅涉及输入的空间和输出的空间，而且涉及状态的空间，并且状态的空间起着重要作用。简单循环神经网络对依次给定的输入的实数向量序列 ${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{T}}$，首先依次生成状态的实数向量序列 ${\mathbf{h}}_1,{\mathbf{h}}_2,\cdots ,{\mathbf{h}}_{\mathbf{T}}$，然后再依次生成输出的概率向量序列 ${\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_{\mathbf{T}}$。在这个过程中，起核心作用的是
$${\mathbf{h}}_{\mathbf{t}}=\text{tanh}(\mathbf{U}\cdot {\mathbf{h}}_{\mathbf{t}-1}+\mathbf{W}\cdot {\mathbf{x}}_{\mathbf{t}}+\mathbf{b})$$的非线性变换，意味着当前位置的状态 ${\mathbf{h}}_{\mathbf{t}}$ 由当前位置的输入 ${\mathbf{x}}_{\mathbf{t}}$ 和之前位置的状态 ${\mathbf{h}}_{\mathbf{t}-1}$ 决定。每一个位置的状态表示的是到这个位置为止的序列数据的局部特征及全局特征，也称作短距离依存关系和长距离依存关系。

循环神经网络的计算需要在序列数据上依次进行。循环神经网络的优点是可以处理任意长度的序列数据，缺点是不能进行并行化处理以提高计算效率。

---

理解简单循环神经网络

NumPy 实现

我们用 Numpy 来实现一个简单 RNN 的前向传递。这个 RNN 的输入是一个张量序列，我们将其编码成大小为 (timesteps, input_features) 的二维张量。它对时间步（timestep）进行遍历，在每个时间步，它考虑 t 时刻的当前状态与 t 时刻的输入［形状为 (input_ features,)］，对二者计算得到 t 时刻的输出。然后，我们将下一个时间步的状态设置为上一个时间步的输出。对于第一个时间步，上一个时间步的输出没有定义，所以它没有当前状态。因此需要初始化一个全零向量，这叫做网络的初始状态。

import numpy as np

timesteps = 100
input_features = 32
output_features = 64

inputs = np.random.random((timesteps, input_features))

state_t = np.zeros((output_features,)) # 初始状态

W = np.random.random((output_features, input_features))
U = np.random.random((output_features, output_features))
b = np.random.random((output_features,))

successive_outputs = []
for input_t in inputs:
	output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)
	successive_outputs.append(output_t)
	state_t = output_t # 更新状态

final_output_sequence = np.stack(successive_outputs, axis=0)

本例中，最终输出是一个形状为 (timesteps, output_features) 的二维张量，其中每个时间步是循环在 t 时刻的输出。输出张量中的每个时间步 t 包含输入序列中时间步 0~t 的信息，即关于全部过去的信息。因此，在多数情况下，我们并不需要这个所有输出组成的序列，只需要最后一个输出（循环结束时的 output_t），因为它已经包含了整个序列的信息。

keras 实现

上面 Numpy 的简单实现，对应一个实际的 Keras 层，即 SimpleRNN 层。

from keras.layers import SimpleRNN

二者有一点小小的区别：SimpleRNN 层能够像其他 Keras 层一样处理序列批量，而不是像 Numpy 示例那样只能处理单个序列。因此，它接收形状为 (batch_size, timesteps, input_features) 的输入，而不是 (timesteps, input_features)。

与 Keras 中的所有循环层一样，SimpleRNN 可以在两种不同的模式下运行：一种是返回每个时间步连续输出的完整序列，即形状为 (batch_size, timesteps, output_features) 的三维张量；另一种是只返回每个输入序列的最终输出，即形状为 (batch_size, output_features) 的二维张量。这两种模式由 return_sequences 这个构造函数参数来控制。我们来看一个使 SimpleRNN 的例子，它只返回最后一个时间步的输出。

from keras.layers import Embedding, SimpleRNN

model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True)) # 返回完整的状态序列
model.summary()
"""
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding (Embedding)       (None, None, 32)          320000    
                                                                 
 simple_rnn (SimpleRNN)      (None, None, 32)          2080      
                                                                 
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0
_________________________________________________________________
"""

为了提高网络的表示能力，将多个循环层逐个堆叠有时也是很有用的。在这种情况下，需要让所有中间层都返回完整的输出序列。

model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32))

接下来，我们将这个模型应用于 IMDB 电影评论分类问题。首先，对数据进行预处理。

from keras.datasets import imdb
from keras.utils import pad_sequences

max_features = 10000
maxlen = 500
batch_size = 32

(input_train, y_train), (input_test, y_test) = imdb.load_data(
    num_words=max_features)

print(len(input_train), 'train sequences')
print(len(input_test), 'test sequences')

input_train = pad_sequences(input_train, maxlen=maxlen)
input_test = pad_sequences(input_test, maxlen=maxlen)
print('input_train shape:', input_train.shape)
print('input_test shape:', input_test.shape)
"""
25000 train sequences
25000 test sequences
input_train shape: (25000, 500)
input_test shape: (25000, 500)
"""

我们用一个 Embedding 层和一个 SimpleRNN 层来训练一个简单的循环网络。

from keras.layers import Dense

model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])

history = model.fit(input_train, y_train,
                    epochs=10,
                    batch_size=128,
                    validation_split=0.2)

import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

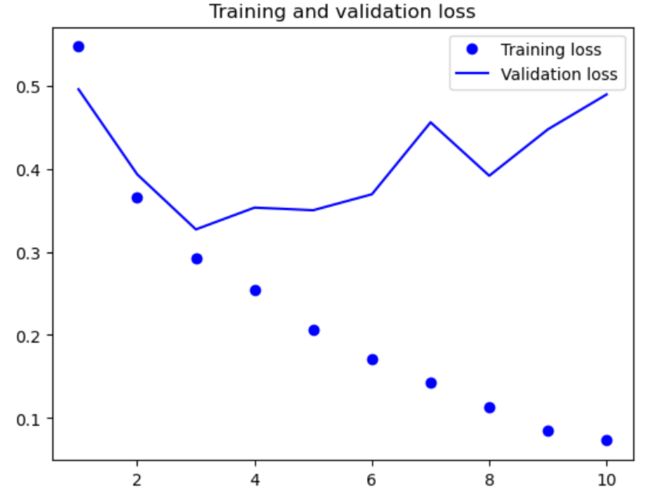
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

---

References

[1] 《Python 深度学习》，François Chollet.
[2] 《机器学习方法》，李航，清华大学出版社。