Self-supervised Graph Neural Networks for Multi-behavior Recommendation-IJCAI 2022 读书笔记

0 作者

Shuyun Gu , Xiao Wang , Chuan Shi${}^{\ast }$ and Ding Xiao

1 动机

• 传统推荐系统一般只考虑购买行为，忽略了放入购物车、浏览行为；
• 本文将购买、放入购物车、浏览三个行为一起考虑；
• 考虑购买和放入购物车行为的差异，进行对比学习；
• 考虑购买和浏览行为的差异，进行对比学习。
  

2 相关工作

Graph Neural Networks(GNN): 参考文献[3]
NGCN: 参考文献[4]
LightGCN: 参考文献[5]

3 主要算法

上图表明将算法主要分为三个部分。图中下标1、2、3分别表示购买、放入购物车、浏览三个行为。

• $\stackrel{◯}{1}$利用GCN对三个行为进行编码，得到$X_1$、$X_2$、$X_3$；
• $\stackrel{◯}{2}$ 求出用户和商品的编码$e_u$和$e_i$；
• $\stackrel{◯}{3}$利用对比学习(Contrastive Learning)来建立购买和放入购物车行为之间的差异、购买和浏览行为之间的差异。

3.1 子图$\stackrel{◯}{1}$

子图$\stackrel{◯}{1}$： 对三个行为编码。
子图$\stackrel{◯}{1}$ 的数据说明：

• $G$：原始数据集，包含用户ID以及他们的购买、放入购物车、浏览三个行为。
• $G_1$：用户和购买关系图；
• $G_2$：用户和放入购物车关系图；
• $G_3$：用户和浏览关系图。
  算法流程：
• 利用GCN对三个行为进行编码，得到$X_1$、$X_2$、$X_3$。

3.2 子图$\stackrel{◯}{2}$

子图$\stackrel{◯}{2}$求用户和商品的编码。 首先将$X_1$、$X_2$、$X_3$拆分为用户在三个行为下的编码$X_{U1}$、$X_{U2}$、$X_{U3}$和商品在三个行为下的编码$X_{I1}$、$X_{I2}$、$X_{I3}$。接下来分别求用户的编码和商品的编码。

3.2.1 对用户编码

• 利用用户$u$的购买、放入购物车、浏览三个行为的编码，对用户$u$进行编码：
  $${\mathbf{e}}_{\mathbf{u}}=\sigma \left\{\mathbf{W}\left(\sum _{k=1}^K{a}_{uk}\ast {\mathbf{x}}_{\mathbf{u}\mathbf{k}}\right)+\mathbf{b}\right\}\text{\hspace{1em}(1)}$$
  – $a_{uk}$：用户$u$的行为$k$对应的权重；
  – ${\mathbf{x}}_{\mathbf{u}\mathbf{k}}$：用户$u$在行为$k$下的编码，来源于$X_{U1},X_{U2},X_{U3}$；
  – $\mathbf{W}$和$\mathbf{b}$：神经网络的权重和偏置；
• 计算$a_{uk}$：分子为单个行为，分母为三个行为的加权累加和。
  $$a_{uk}=\frac{\exp \left(w_k\ast n_{uk}\right)}{{\sum }_{m=1}^K\exp \left(w_m\ast n_{um}\right)}\text{\hspace{1em}(2)}$$
  – $w_k$：行为$k$的权重，作者用的是一个全局的变量，所有用户采用相同的权重值，比如购买是0.5，放入购物车是0.3，浏览是0.2;
  – $n_{u_m}$：用户$u$在行为$m$下的物品个数，比如张三购买了2个商品，将3个商品放入购物车，浏览了5个商品。
• 作者提供的代码里，本部分对应的代码如下。
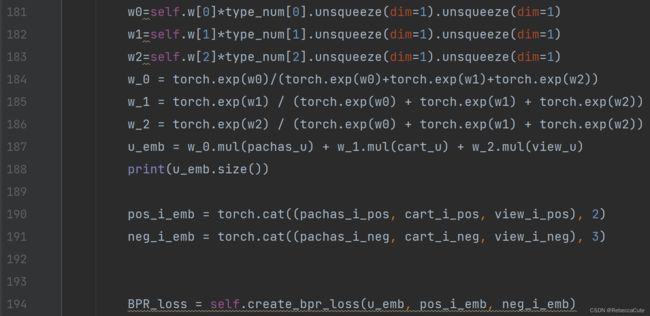
  – Lines181-183是式(2)的分子。在论文里，$n_{uk}$是the number of associations of user $u$ under behavior $k$。但是在作者提供的代码里，使用的是各个行为下物品个数的占比。
  – Lines184-186分别求出$a_{u1}$、$a_{u2}$、$a_{u3}$。Line187 中pachas_u、cart_u以及view_u分别表示用户购买行为、放入购物车行为、浏览行为的编码矩阵。
  – Line187为式(1)中的${\sum }_{k=1}^K{a}_{uk}\ast {\mathbf{x}}_{\mathbf{u}\mathbf{k}}$。

3.2.2 对商品进行编码

• 将第$i$个商品在行为$k$下的编码拼接起来(Cat($\cdot$))，并利用多层感知机$g(\cdot )$计算${\mathbf{e}}_{\mathbf{i}}$。
  $${\mathbf{e}}_{\mathbf{i}}=g\left\{\mathrm{Cat}\left({\mathbf{x}}_{\mathbf{ik}}\right)\right\}\text{\hspace{1em}(3)}$$
• 作者提供的代码里，本部分对应的代码如上图。
  – Line190和Line191是将物品三个行为的编码矩阵按照第二维和第三维进行拼接，得到pos_i_emb和neg_i_emb。
  – Line194计算BPR loss。将Lines 187、190、191的$u\_emb$、$pos\_i\_emb$、$neg\_i\_emb$作为输入，带入BPR loss计算式中，求得BPR loss。

3.3 子图$\stackrel{◯}{3}$

子图$\stackrel{◯}{3}$ 为利用constractive learning计算两两行为之间的差异：购买和放入购物车之间的差异、购买和浏览之间的差异。以下分两个方面考虑：用户购买和放入购物车之间的差异、购买和浏览之间的差异以及商品被购买和被放入购物车之间的差异、被购买和被浏览之间的差异。

3.3.1 计算用户购买和放入购物车之间的差异、购买和浏览之间的差异

计算式如下：
$${\mathcal{L}}_{sst\_k^{\prime }}^{user}=\sum _{u\in U}-\log \frac{{\sum }_{u^{+}\in U}\exp \left\{{\left({\mathbf{x}}_{\mathbf{u}1}\right)}^T{\mathbf{x}}_{{\mathbf{u}}^{+}{\mathbf{k}}^{\prime }}/\tau \right)\}}{{\sum }_{u^{-}\in U}\exp \left\{{\left({\mathbf{x}}_{\mathbf{u}1}\right)}^T{\mathbf{x}}_{{\mathbf{u}}^{-}{\mathbf{k}}^{\prime }}/\tau \right\}}\text{\hspace{1em}(4)}$$
– $k^{\prime }$：取值为2和3，2代表放入购物车，3代表浏览；
– $u^{+}$和$u^{-}$：以用户$u$为基础，找到用户$u$的正用户集和负用户集，$PMI$值用于衡量两个用户$u$和$u^{\prime }$的相似度。当该大于某个阈值时，$u^{\prime }$为$u$的正用户，否则为$u$的负用户。计算方法如下：
$$\begin{array}{c}PMI\left(u,u^{\prime }\right)=\log \frac{p\left(u,u^{\prime }\right)}{p(u)p\left(u^{\prime }\right)}\\ p(u)=\frac{|I(u)|}{|I|}\\ p\left(u,u^{\prime }\right)=\frac{|I(u)\cap I\left(u^{\prime }\right)|}{|I|}\end{array}\text{\hspace{1em}(5)}$$
式(5)中第一行对数后方的分子：为式(5)中第三行。式(5)中第三行计算两个用户$u$和$u^{\prime }$的相似度，其分子为两个用户在同一个行为下的相同商品的个数，分母为所有商品的个数。
式(5)中第一行对数后方的分母：为式(5)中第二行。计算用户$u$在某个行为下的商品个数/所有商品的个数。
– $\tau$：温度参数，作者的代码里$\tau$取值为1。

3.3.2 计算商品被购买和被放入购物车之间的差异、被购买和被浏览之间的差异

• 计算商品被购买和放入购物车之间的差异、商品被购买和浏览之间的差异，计算方法与用户类似。 计算式如下：
  $${\mathcal{L}}_{sst\_k^{\prime }}^{item}=\sum _{i\in I}-\log \frac{{\sum }_{i^{+}\in I}\exp \left\{{\left({\mathbf{x}}_{\mathbf{i}1}\right)}^T{\mathbf{x}}_{{\mathbf{i}}^{+}{\mathbf{k}}^{\prime }}/\tau \right)\}}{{\sum }_{i^{-}\in I}\exp \left\{{\left({\mathbf{x}}_{\mathbf{i}1}\right)}^T{\mathbf{x}}_{{\mathbf{i}}^{-}{\mathbf{k}}^{\prime }}/\tau \right\}}\text{\hspace{1em}(6)}$$

3.3.3 Contrastive learning中的问题

在作者提供的代码里，并没有看到PMI的计算。式(4)和(6)也与代码不一致。在代码里，Contrastive learning 的计算步骤为：

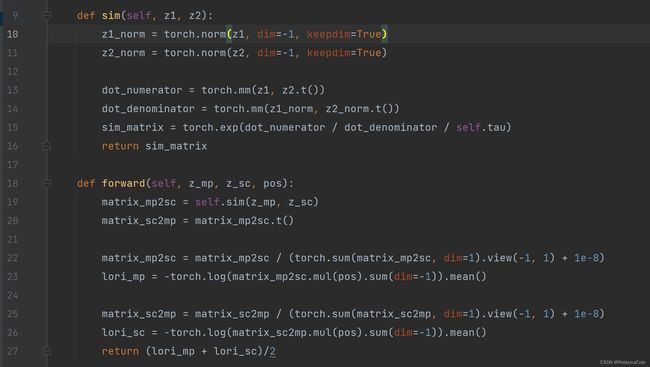
1. Line 19调用Lines 9-16计算两个行为的相似度矩阵sim()
   Lines10-11：分别计算用户在两个行为下的二范数。
   Lines13-14：(未完待续)
2. 计算…(未完待续)

3.4 损失函数

总的损失函数如下：
$$\mathcal{L}={\mathcal{L}}_{st}+\lambda {\mathcal{L}}_{sst}+\mu \Vert \Theta {\Vert }_2^2\text{\hspace{1em}(8)}$$
第一项为BPR Loss：
$${\mathcal{L}}_{st}=\sum _{(u,i,j)\in O}-\log \left\{\sigma \left(e_u^T{e}_i-e_u^T{e}_j\right)\right\}\text{\hspace{1em}(9)}$$

• $e_u$：用户$u$的编码；
• $e_i$：用户$u$购买过、或放入购物车、或浏览过的商品编码；
• $e_j$：用户$u$未购买过、或未放入购物车、或未浏览过的商品编码，作者在代码里面选的64个未产生过行为的商品。

第二项为对比学习产生的Loss:
$${\mathcal{L}}_{sst}=\sum _{k^{\prime }=2}^K\left({\mathcal{L}}_{sst-k^{\prime }}^{user}+{\mathcal{L}}_{sst-k^{\prime }}^{item}\right)\text{\hspace{1em}(10)}$$

• ${\mathcal{L}}_{sst\_k^{\prime }}^{user}$：同公式(4)；
• ${\mathcal{L}}_{sst\_k^{\prime }}^{item}$：商品的Loss。

参考文献

[1] Self-supervised Graph Neural Networks for Multi-behavior Recommendation
[2] 源代码：https://github.com/GuShuyun/MBRec
[3]Chen Gao, Yu Zheng, Nian Li, Yinfeng Li, Yingrong Qin, Jinghua Piao, Yuhan Quan, Jianxin Chang,
Depeng Jin, Xiangnan He, et al. Graph neural networks for recommender systems: Challenges, methods, and directions.arXiv preprint arXiv:2109.12843, 2021.
[4]Xiang Wang, Xiangnan He, Meng Wang, Fuli Feng, and Tat-Seng Chua. Neural graph collaborative filtering. In Proceedings of the 42nd international ACM SIGIR conference on Research and Development in Information Retrieval, pages 165–174, 2019.
[5]Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, Yongdong Zhang, and Meng Wang. LightGCN:
Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, pages 639–648, 2020.