图像分类算法:GoogLeNet论文解读
图像分类算法:GoogLeNet论文解读
前言
其实网上已经有很多很好的解读各种论文的文章了,但是我决定自己也写一写,当然,我的主要目的就是帮助自己梳理、深入理解论文,因为写文章,你必须把你所写的东西表达清楚而正确,我认为这是一种很好的锻炼,当然如果可以帮助到网友,也是很开心的事情。
说明
如果有笔误或者写错误的地方请指出(勿喷),如果你有更好的见解也可以提出,我也会认真学习。
原始论文地址
点击这里,或者复制链接
https://arxiv.org/pdf/1409.4842.pdf
目录结构
文章目录
-
- 图像分类算法:GoogLeNet论文解读
-
- 1. 背景简介:
- 2. 文章内容概述:
- 3. 作者的思路来源:
- 4. 提高神经网络性能的最直接方法:
- 5. Inception介绍:
-
- 5.1 1*1卷积核的作用:
- 6. GoogLeNet介绍:
- 7. 总结:
1. 背景简介:
CNN在快速发展,而这种发展并不是单纯的利用更强的算力、更大的数据集、更大的模型,而是探索着新思想、新算法和新的网络结构。
而作者发现算法效率(功耗和内存)越来越重要。因为人们不仅仅只追求试验上的好效果,还追求应用于工业中,这就要求算法的效率必须高。
基于这种想法和前人的工作,作者提出了GoogLeNet。
2. 文章内容概述:
作者提出了一个名为Inception的新CNN架构,其核心特点是提高网络内计算资源的利用,并以此提出了名为GoogLeNet的模型,在2014年的ImageNet比赛上取得了第一名的成绩(第二名为VGG)。
3. 作者的思路来源:
- 算法效率的重要性
- 前人采用了一系列大小不同的卷积核实现多尺度目的
- Hebbian原则与多尺度处理
- Network-in-Network
解释:Hebbian原则
简单来说,就是只考虑局部,不考虑整体。比如对于一个神经网络,一般来说调整权值是整体调整,但是Hebbian原则则是只考虑一个神经元,其通过比较输入与输出来调整权值。
即,通过局部最优来构造整体最优。(需要进行证明,见后文)
Network-in-Network
即网络中有网络,用GooLeNet模型来说,就是整个GoogLeNet是由一系列相同的小网络构成。
4. 提高神经网络性能的最直接方法:
最简单、最直接的方法就是增加网络深度(层数)和宽度(每层中的个数)。
但是这会导致两个主要缺点:
- 参数量大,容易过拟合且不易训练
- 计算资源急剧增加
那么,这两个缺点有什么解决办法呢?我们知道,CNN架构的模型参数量主要集中在FC层,而解决这个问题的一个方法就是**将全连接架构转为稀疏连接架构(本质上就是减少参数量)。**但是,目前计算机计算稀疏矩阵是低效的(应该是针对大数据而言)。而基于Hebbian原则和作者引用的一篇论文,作者提出了Inception的架构。
解释:Arora的论文(作者引用的)
该论文表明:如果数据集的概率分布可以用一个大型、稀疏的深度神经网络表示,那么可以通过分析最后一层的激活和聚合有高度相关输出的神经元的统计数据,一层一层的构建最优网络结构。
这一点和Hebbian原则有相似性。
5. Inception介绍:
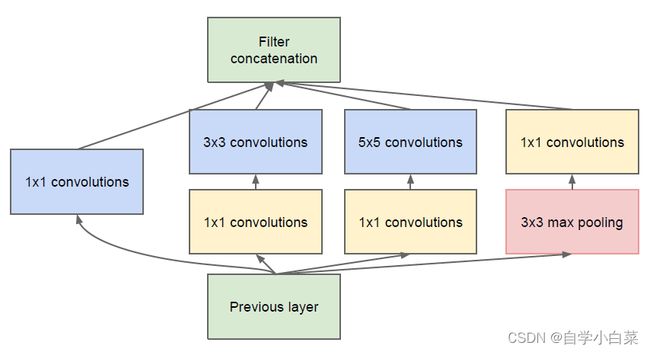
论文原图如下:
Inception的结构分为四条路线,代表着四种处理角度,是一种多尺度手段。
前一层的输出经过四条路线处理后,需要保证输出的维度相同,这样通过最后的拼接操作可以将四条线路的结果拼接在一起。
5.1 1*1卷积核的作用:
在VGG中,也用到了1*1卷积核,不过这里则是更加深入。
作用如下:
- 在相同的感受野中获得更多的特征<==>增加非线性变换,获取更多特征
解释:感受野
简单来说,卷积神经网络每一层输出的特征图上的像素点在输入图片上映射的区域大小。
一个小例子:假设一个输入图像大小为227*227*3,经过一个卷积操作(3*3*128,S=2,P=0),那么输出为113*113*128。
(227-3)/2 + 1 = 113
那么,输出的整张图(姑且称为图)一个小单元格,可以大约代表2个原图像的位置,这就是此时它的感受野。
解释:1*1作用1
这里的意思是,原来只有一个卷积层,此时我们在它前面或者后面添加一个1*1卷积层。而1*1卷积不会改变输出大小,但是多了一次卷积的过程(此时可以视为线性操作),而卷积后一般会接上ReLU激活函数,相当于多了一次非线性变换。这样可以提取到更多的信息。
- 另外一个作用就是降维,这得益于1*1卷积核不改变输出大小,但是可以改变通道数的特点
解释:1*1降维的好处
降维,意味着可以放心的为每个阶段增加单元数量(加宽),这意味着更好的性能。
6. GoogLeNet介绍:
GooLeNet中的大写L是向LeNet表示敬意。
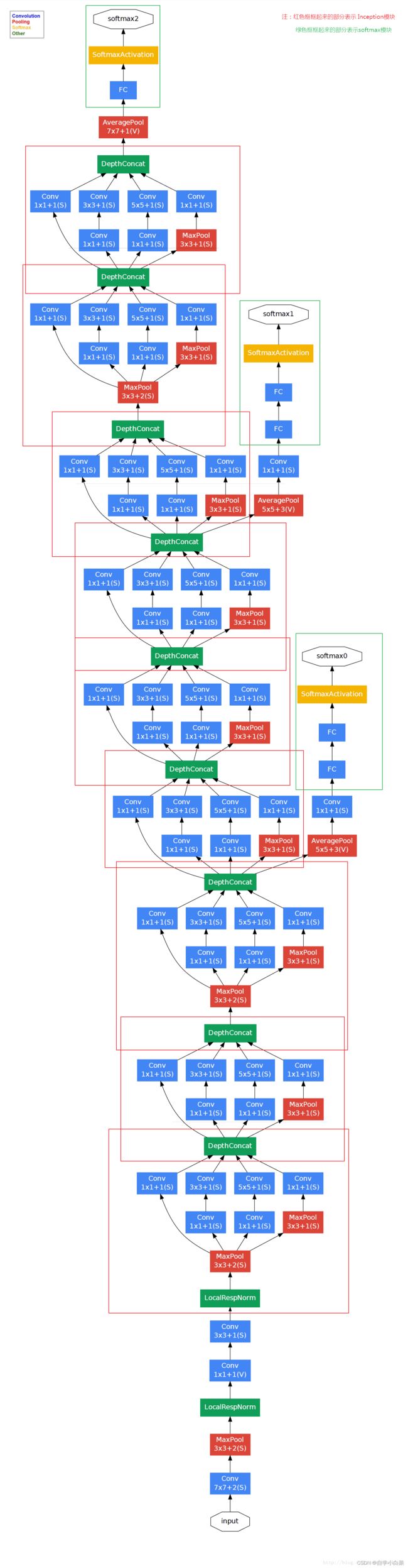
而GoogLeNet是由Inception组成的,具体结构如下图,也是论文原图:
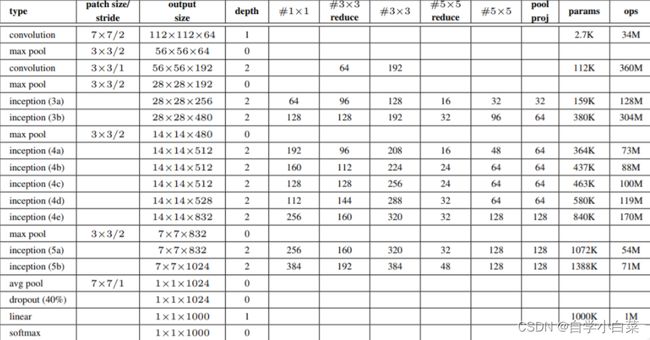
具体的参数可以看下表:
对于GoogLeNet需要说明以下几点:
- 为什么不一上来就使用Inception架构?
作者给出的原因是内存影响,具体为什么我也不清楚,知道的可以在评论区解释下。
- 分支的作用:在GoogLeNet中有几个分支,有什么作用呢?
由于网络很深,想要有效的进行BP是困难的,因此作者考虑到中间层的输出与最终的输出是有区别的,因此借用分支,可以为顶层的BP提供正则化的操作。
- 上图中的字母
s\v含义:
首先,需要知道特征图尺寸计算两种模式:
v : valid,此时输出大小=(输入大小-卷积核大小)/步长 + 1
s : same,此时输出大小=(输入大小-卷积核大小+2*padding)/步长 + 1
恰好这就是字母的含义,另外值得一提的是当尺寸不被整除时,卷积向下取整,池化向上取整
参考文章:https://blog.csdn.net/weixin_39881922/article/details/80732559
7. 总结:
GoogLeNet算是一种新的架构方式,其中涉及的方法诸如Network-in-Netiwork、1*1卷积核的使用、多尺度方法等在后续也是常用的手段。