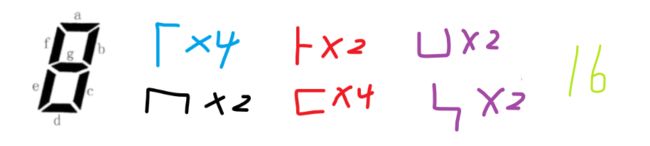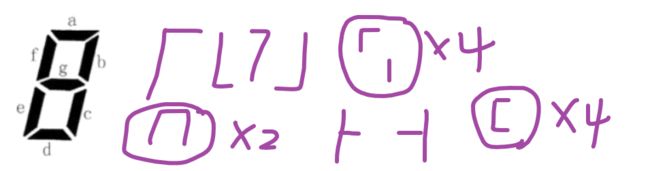蓝桥杯第13天(Python版)
计算有多少约数
能被整除的数就是约数,包括1和本身
ans = 0
for i in range(1,1200000+1):
if 1200000 % i == 0:
ans += 1
print(ans)计算特殊时间(手算题)
ans =4*(4*(1+1+1+1+1+1+1+1+1)+3+2+2+3+2+2)
# 0111 0222 1011 1101 1110 1112 1121 1211 1222
# 1113 1114 1115 1131 1141 1151
# 年不受限制,
# 月:1-12
# 日:1-30/28/31
# 时:0-23
# 分:0-59
print(ans)
组合型枚举模板(DFS)
chosen=[]
n 总共n个数
m 选取m个数
def calc(x): # 从x开始选取
if len(chosen)>m: # 选取了大于m个数
return
if len(chosen)+n-x+1排列性枚举
vis = [0]*100 # 用来标记是否访问
chosen = []
def dfs(n):
if(len(chosen)==4): # 选取了4个,退出
print(*chosen)
return
for i in range(1,5):
if vis[i]==0: #没有被选取
chosen.append(i) # 选该元素
vis[i]=1
dfs(n+1)
chosen.pop() # 不选该元素
vis[i]=0
dfs(1) # 手写全排列[ 1 2 3 4 ]
######### 用到了n,其中n来标记第n为取值情况 ########
vis = [0]*100 # 用来标记是否访问
chosen = [0]*100
def dfs(n):
if(n==5): # 选取了4个,退出
print(chosen[1:5])
return
for i in range(1,5):
if vis[i]==0: #没有被选取
chosen[n]=i
vis[i]=1
dfs(n+1)
chosen[n]=0
vis[i]=0
dfs(1) # 手写全排列[ 1 2 3 4 ]
双指针计算美丽区间(双针针或者暴力)
双指针,一个右,一个左,一直向右移动
import os
import sys
# 暴力法双重循环遍历
# ans = 1000 # 保存最小美丽区间长度
# n,s = map(int,input().split())
# l = list(map(int,input().split())) # 存数组
# for i in range(1,n): # 右指针
# for j in range(0,i):
# if sum(l[j:i+1])>=s:
# ans = min(i-j+1,ans)
# if ans==1000:
# print(0)
# else:
# print(ans)
# 尺取法
ans = 1000
n,s = map(int,input().split())
word = list(map(int,input().split())) # 存数组
l,r = 0,0
while r <= n-1:
while sum(word[l:r+1])=s : #移动l,直到不满足条件
l+=1
ans = min(r-(l-1)+1,ans)
r+=1
if ans==1000:
print(0)
else:
print(ans)
#正确的尺取法,前面那个求和复杂度高了,即需要维护前缀和
n,s = map(int,input().split())
a = list(map(int,input().split()))
SUM = 0
ans = 1e5
left,right=0,0
while(right判断回文
转为字符串或者列表,通过切片取反操作直接判断
import os
import sys
# 请在此输入您的代码
s = input()
if s==s[::-1]:
print("Y")
else:
print("N")局部变量和全局变量
data = [0 for i in range(5) ]
cnt = 0
def fib(n):
global cnt
cnt =3 #局部变量
data[n]=1 # 并未创建变量,直接修改的全局变量
print(cnt)
print(*data)
fib(2)
print("------分界线------")
print(cnt)
print(*data)
# 3
# 0 0 1 0 0
# ------分界线------
# 3
# 0 0 1 0 0
#没有global声明
# 3
# 0 0 1 0 0
# ------分界线------
# 0
# 0 0 1 0 0数的计算
读懂题意,只需判断首位,有循环重复操作直接递归函数
# 只需要判断首位
def f(n):
global res
if n == 1:
return
for i in range(1, n//2+1): # 范围[1,n//2]
res += 1
f(i)
n = int(input())
res = 1
f(n)
print(res)
# 6 1
# 16 26 36 3
# 126 136 2
# 总共6个数的划分
n, k = map(int, input().split())
# 初始化一个二维数组,用于存储 f(n, m)
dp = [[0]*210 for i in range(210)]
for i in range(1, n+1): #初始化操作
dp[i][1] = 1 #分成1块的分法
dp[i][i] = 1 #分成n块的分法
for i in range(3, n+1): # 分成块的数量
for j in range(2, k+1): # 总数量
if i > j:
dp[i][j] = dp[i-j][j] + dp[i-1][j-1]
print(dp[n][k])耐摔指数(国赛4/5题,太难)
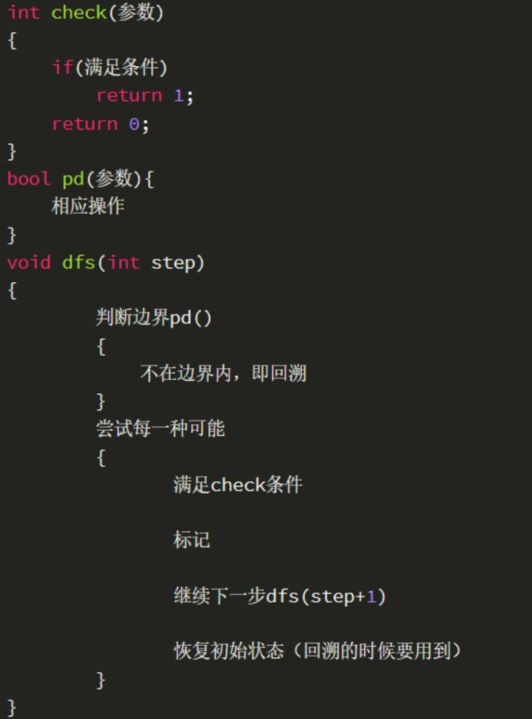
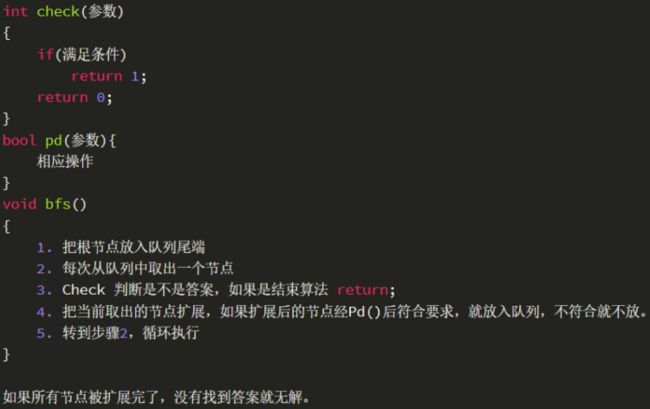
DFS与BFS编写框架
DFS(用于寻找路径条数)
BFS(用于寻找最短路径)
迷宫问题
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000DFS肯定超时,BFS搜索,重点在于保存路径???
官方解题思路: BFS 搜索记录路径,用 DFS 打印路径。
这道题属于DFS和BFS结合的问题,在BFS遍历过程中找到最短路径,同时保存路劲,后续用DFS从终点开始搜索路径
import collections
mp = [] #存地图 30行50列
for i in range(30):
mp.append(list(map(int,input())))
k = ('D','L','R','U') # 下,左,右,上
dir = [(1,0),(0,-1),(0,1),(-1,0)] # 下为x正方向,右为y正方向
vis = [[0]*50 for i in range(30)] # 标记数组
father = [['']*50 for i in range(30)]
def dfs(x,y): # 回退搜索以前的路径
if x==0 and y==0:
return
if father[x][y] =='D': dfs(x-1,y)
if father[x][y] =='L': dfs(x,y+1)
if father[x][y] =='R': dfs(x,y-1)
if father[x][y] =='U': dfs(x+1,y)
print(father[x][y],end='')
def bfs(x,y):
global father
global vis
q = collections.deque()
q.append((x,y)) # 遍历该点
vis[x][y] = 1
while q:
now = q.popleft()
if now[0]==29 and now[1] ==49 :# 到达终点
return
for index in range(4): # 4个方向遍历
i=dir[index]
nx = now[0]+i[0];ny = now[1]+i[1]
if nx<0 or nx >=30 or ny<0 or ny>=50 : #超出了边界
continue
if vis[nx][ny]==1 or mp[nx][ny] ==1: # 判断是否走过或者碰到了边界
continue
vis[nx][ny]=1
q.append((nx,ny)) # 将当前点添加进队列
father[nx][ny]=k[index] # 添加进父,便于DFS寻找
bfs(0,0)
dfs(29,49)
跳蚂蚱问题
转为移动空盘子问题
题目给的是一个圆圈,不好处理,用一个建模技巧“化圆为线”,把圆形转换为线形。把空盘看成 0,那么有 9 个数字 {0,1,2,3,4,5,6,7,8},一个圆圈上的 9 个数字,拉直成了一条线上的 9 个数字,这条线的首尾两个数字处理成相连的。
这一题是八数码问题,八数码是经典的 BFS 问题。八数码问题有 9 个数字{0, 1, 2, 3, 4, 5, 6, 7, 8},共有 9!= 362880 种排列,不算多。
本题的初始状态是“012345678”,目标状态是“087654321”。从初始状态“012345678”跳一次,有 4 种情况:“102345678”、 “210345678”、 “812345670”、 “712345608”。然后从这 4 种状态继续跳到下一种状态,一直跳到目标状态为止。
用 BFS 扩展每一层。每一层就是蚱蜢跳了一次,扩展到某一层时发现了终点“087654321”,这一层的深度就是蚱蜢跳跃的最少次数。
#半成品,错误的
a=[i for i in range(1,9)]
a=[0]+a
# print(a)
ans,count=10000,0
def dfs():
if a==[0,8,7,6,5,4,3,2,1]:
ans = min(ans,count)
dfs()list写法:
def insertQueue(q: list, dir: int, news: tuple, vis):
pos = news[1] # 0的位置
status = news[0]
insertPos = (pos + dir + 9) % 9
# 将字符串转为列表比较好处理
t = list(status)
t[pos], t[insertPos] = t[insertPos], t[pos]
addStatus = "".join(t)
if addStatus not in vis:
vis.add(addStatus) #用字典判重,改为:vis[addStatus]=1 向字典添加
q.append((addStatus, insertPos, news[2] + 1))
# main
q = [("012345678", 0, 0)]
vis = set(); vis.add("012345678") #用字典判重,改为:vis = {"012345678":1}
while q:
news = q.pop(0)
if news[0] == "087654321": #到达了目标状态,输出最少步数
print(news[2])
break
insertQueue(q, -2, news, vis) #扩展下一层的4种情况
insertQueue(q, -1, news, vis)
insertQueue(q, 1, news, vis)
insertQueue(q, 2, news, vis)deque写法:
from collections import *
def insertQueue(q: deque, dir: int, news: tuple, vis: set):
pos = news[1]; status = news[0]; insertPos = (pos + dir + 9) % 9
t = list(status)
t[pos], t[insertPos] = t[insertPos], t[pos]
addStatus = "".join(t)
if addStatus not in vis:
vis.add(addStatus)
q.append((addStatus, insertPos, news[2] + 1))
q = deque()
q.append(("012345678", 0, 0))
vis = set(); vis.add("012345678")
while q:
news = q.popleft()
if news[0] == "087654321": print(news[2]); break
insertQueue(q, -2, news, vis); insertQueue(q, -1, news, vis)
insertQueue(q, 1, news, vis); insertQueue(q, 2, news, vis)七段码问题(手数)
根据亮的情况依次画图,可以反推熄灭几个灯,注意亮着的必须连续就行
亮1 7
亮2 10
亮3 16
亮4的情况 16 20
补:
亮5 19
亮6熄1 7
亮7熄0 1
#有问题,答案错(7+10+16+16+19+7+1=76),正确答案80
#改正(7+10+16+20+19+7+1=80)
N皇后问题
#初学者写法(菜),而且有问题,只通过了一个测试点
import os
import sys
# 请在此输入您的代码
# DFS问题
def dfs(y):
global ans
if y==n+1:
ans+=1
return
for k in range(1,y):
if abs(y-k)==abs(save[y]-save[k]): #判断是否在斜线上
return
elif save[k]==save[k]: # 位于同一列了
return
for i in range(1,n+1):
if vis[i]==0:
save[y]=i # 第y行的皇后放在k位置
vis[i]=1
dfs(y+1)
vis[i]=0
n = int(input())
save = [0]*20 #保存每行的皇后的列位置
ans = 0
vis =[0]*20 # 判断是否访问过
for i in range(1,n+1): # 从1-n
dfs(i)
print(ans) # 打印多少种方式注意设置最大递归深度 。sys.setrecursionlimit(3000000)
标准答案:
import sys
sys.setrecursionlimit(1000000) # DFS一般要设置好最大递归深度
x = [0]*15
sum = 0
def pd(k):
for i in range(1,k): #判断前k个
if abs(k-i) == abs(x[k]-x[i]): # 判断斜45°
return 0
elif x[k]==x[i]: # 判断同列
return 0
return 1
def check(a): # 检查是放好第n层
if a>n:
global sum
sum+=1
return True
else:
return False
def DFS(a):
if check(a):
return
else:
for i in range(1,n+1): # 遍历每列
if(pd(a)): # 满足条件
x[a]=i
DFS(a+1) #搜索下一行
x[a]=0
else:
continue
n = int(input())
DFS(1)
print(sum)
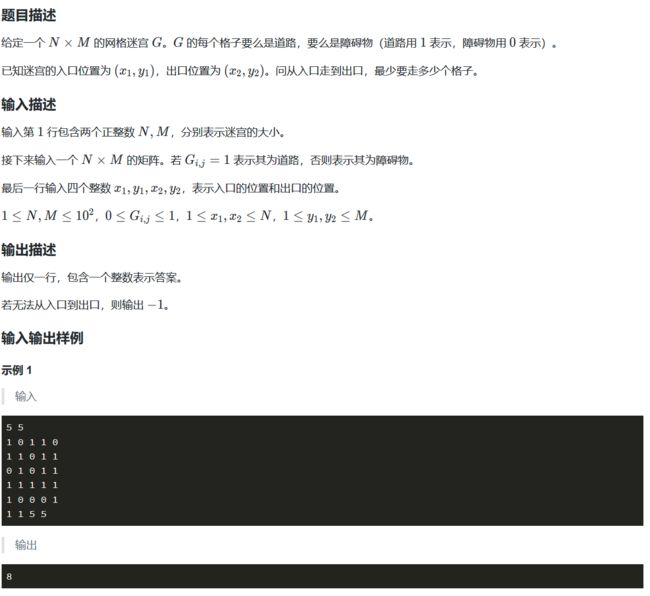
走迷宫问题
#有问题的代码,错误的,用错误的提醒自己
import sys
import collections
sys.setrecursionlimit(10000000)
n,m = map(int,input().split()) # 读入地图的大小
mp = []
ans = 0 #记录步数
save=collections.deque()
for i in range(m):
mp.append(list(map(int,input().split())))
x1,y1,x2,y2 = map(int,input().split())
vis =[ [0]*1000 for i in range(1000)] # 创建一个更大的标记数组
walk = [(0,1),(-1,0),(0,-1),(1,0)] # 四个方向
def bfs(x,y):
global ans
if x==x2 and y==y2: #到达终点
return ans
for dx,dy in walk: # 开始遍历
if 0<=x+dx<=m-1 and 0<=y+dy<=n-1 : # 判断坐标合法
bfs(x+dx,y+dy)
ans+=1
bfs(x1,y1)
print(ans)
改正写法:也存在问题,问题在判断上一层是否出队列完,即走的步数判断问题
以改正,关键思想是,将步数信息直接加在队列里面,即(x,y,length)
import collections
mp = [] #存地图 n行m列
n,m = map(int,input().split())
for i in range(n): # 读地图
mp.append(list(map(int,input().split())))
x1,y1,x2,y2 = map(int,input().split())
dir = [(1,0),(0,-1),(0,1),(-1,0)] # 下为x正方向,右为y正方向
vis = [[0]*200 for i in range(200)] # 标记数组
ans = 0
flag=0
def bfs(x,y):
global vis,ans,flag
q = collections.deque()
q.append((x,y,0)) # 遍历该点
vis[x][y] = 1
while q:
now = q.popleft()
if now[0]==(x2-1) and now[1] ==(y2-1) :# 到达终点(x2,y2)
flag = 1
ans=now[2]
break
for index in range(4): # 4个方向遍历
i=dir[index]
nx = now[0]+i[0];ny = now[1]+i[1]
if nx<0 or nx >=n or ny<0 or ny>=m : #超出了边界
continue
if vis[nx][ny]==1 or mp[nx][ny] ==0: # 判断是否走过或者碰到了边界
continue
vis[nx][ny]=1
q.append((nx,ny,now[2]+1)) # 将当前点添加进队列
bfs(x1-1,y1-1) # 从x1,y1搜索到x2,y2
if flag==0:
print(-1)
else:
print(ans)错误代码第二天修改!!!!错误答案提醒自己!!