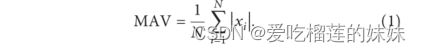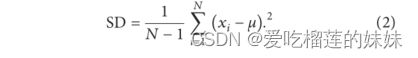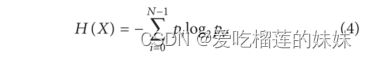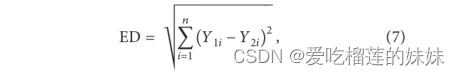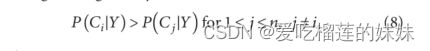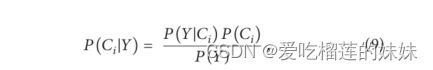011小波域和机器学习在脑电信号癫痫发作检测中的应用-2022
On the Use of Wavelet Domain and Machine Learning for the
Analysis of Epileptic Seizure Detection from EEG Signals
癫痫患者的脑部癫痫发作是由暂时和不可预知的电中断引起的。
传统上,脑电信号记录来自大脑的电活动,由医务人员手动学习,㼿技术耗时长,输出不可靠。为了解决这一问题,本研究提出了一种新的癫痫发作检测结构,使用来自德国波恩大学的脑电信号和印度Senthil综合专科医院的实时医疗记录,将信号分解成6个频率子带,采用离散小波变换提取12个统计函数。
特别是,确定了7个最佳特征,并进一步将其输入到k近邻、朴素贝叶斯、支持向量机和决策树分类器中,用于两种类型和三种类型的分类。使用了六个统计参数来衡量这些分类的性能。已经发现,特征和分类器的不同组合产生不同的结果。总体而言,这项研究是为波恩和Senthil实时临床数据集的16个不同的2类和3类分类挑战找到最佳组合特征集和分类器的首次尝试。
1. Introduction
癫痫是一种大脑疾病,包括由于不受控制的电运动导致的大脑中的反复发作。它导致不受约束的抽搐运动和短暂的意识丧失。它具有潜在的生命威胁,因为它会导致大脑和肺部功能障碍、心力衰竭和意外死亡。因此,当务之急是诊断癫痫[1]。记录大脑中电运动和活动的信号是脑电图(EEG)信号。在这个过程中,电极被放置在头皮的不同部位,产生多通道数据。由于这是一种非侵入性和廉价的方法,它在癫痫检测等神经病学诊断中起着重要的数据来源的作用[1,2]。通常,医务人员通过视觉检查长期EEG来收集记录。这个方法耗时、繁琐且容易出错,并且需要一定的专业水平。因此,需要一个自动癫痫发作检测框架。
这由医生读取脑电记录以确定癫痫病情的繁琐性质,因此有必要研究更直接、更快、更有效地检测癫痫病情的方法。在文献[3]中,进行了一种模式识别研究,它使用时间域(TD)函数来检测癫痫发作,包括波形长度(WL)、一些斜率符号变化(SSC)和许多过零点(ZC),这些都是滤波后的脑电数据的导数,用于检测癫痫发作的滤波脑电数据的离散小波变换(DWT)。为此,研究了基于支持向量机和朴素贝叶斯(NB)的特征提取方法。结果表明,对于常规睁眼和癫痫数据集,对于直接TD函数和基于离散余弦变换的TD函数,建议的方法应该达到100%的最佳准确率。
在文献[4]中,将脑电与深度学习计算技术相结合来诊断癫痫发作已势在必行。研究强调设计和评估基于深度卷积神经网络的癫痫发作检测方法。提出的结果是确定最准确的癫痫发作检测方法,并将其分为三种方法。最高平均分类正确率为99.21%,结果表明,信号-图像转换方法和正确率数据模型的比较结果在绝大多数情况下都超过了以往的研究。此外,为了找出最好的分类精度和脑电信号的频率特征,使用了Shapley Additive Informance(Shap)分析方法。
在[5]中,波恩数据集被用来评估新建议的自动记录癫痫脑电信号的技术。基于近似熵和重复混合量化分析,利用卷积神经网络。结果表明,近似熵和重复量化能够有效地检测癫痫发作。经典记录自动区分癫痫脑电信号和卷积神经网络,特别是结合近似熵和递归量化分析特征时,结果分别达到98.84%、99.35%和99.26%。这一领域的其他几项工作都表明,癫痫状态的自动检测是可能的,从而排除了医生检查脑电的繁琐任务。工具将有助于癫痫的临床诊断和治疗。
在提供准确的解决方案的问题上。癫痫发作,已经提出了几种算法,并且。它们提供了几个级别的准确性。在[6-8]中,有几个将时频域算法引入到信号处理中。从收集到的脑电信号癫痫发作的准确特征。其中两种算法是短时傅里叶变换和多小波变换,这两种算法经过验证取得了令人满意的结果。离散小波变换在[9]中被用于癫痫发作的检测,首先使用此方法从脑电信号中提取特征,然后进行主成分分析、独立成分分析,最后引入线性判别分析,以降低各种信号的维度,便于直观地表示。然后利用支持向量机学习模型对多维平面上的混合脑电信号进行分类。
如前所述,支持向量机对于信号分类是有效的,但这并不是没有选择最佳参数数量的挑战。设置合适的参数是实现高精度癫痫发作检测的关键。超参数的调整和选择,使得粒子群优化和遗传算法具有很高的精度。癫痫发作的检测必须准确和高效,这就是为什么最近引入了机器学习算法。算法可以准确地处理用于脑电信号的大量数据集。
此外,ML算法提供的健壮网络结构使其在表征脑电信号时具有可伸缩性和实用性。癫痫发作检测必须以最低的假阴性和假阳性进行。在[9,10]中引入的离散小波变换能够处理癫痫发作中的棘波问题。离散小波变换算法可以通过对这些瞬变事件的局部化来处理尖峰信号。算法防止了尖峰事件的泛化,从而减少或最小化了信号表征过程中特定时刻的任何形式的误差。
采用混合方法对癫痫发作进行检测[11],将遗传算法嵌入到模糊逻辑中,对癫痫和非癫痫信号进行特征提取。通过将数据融合到遗传算法中以做出准确的预测,提供了对两种信号特征(癫痫和非癫痫)的各种风险评估。另一种混合方法是在[12]中引入的,其中计算智能与遗传算法相结合以确保脑电信号的最优特征。整个数据集被分为训练和验证数据集。从数据集中提取特征并用于训练遗传算法,然后使用验证数据集对训练后的模型进行验证,基于遗传算法的模型能够准确地检测癫痫发作。混合模型的效率很高,可以充分弥补每个基础模型的不足,从而产生一个精度较高的单一模型。对于这一特定的基本模型,精度在很大程度上取决于遗传算法参数的适当调整。
文献[13]中引入了另一种模型平稳小波变换,并将其用于癫痫发作的检测。该算法正确地捕获了信号边缘上在所有点上都是平稳的点。捕获这些平稳点的能力降低了错误概率。这是因为小波上通常不会被计算在内的点现在已经通过这种平稳小波算法得到了充分的表示。在不同条件下对癫痫信号和非癫痫信号进行处理,以确定其最优水平。平稳小波算法也能有效地处理沿粗糙边缘的数据点,这可能会对癫痫发作检测算法产生负面影响。然而,对于线性信号和非线性信号,也可以用平稳小波变换来适当地处理它们。
文献[14]中给出了一种检测癫痫发作的算法。研究使用癫痫患者和非癫痫患者的数据来建立框架。作者使用线性和非线性分类器将样本特征分类到不同的数据集。线性分类器处理来自非癫痫患者的测量数据,而非线性分类器用于对癫痫患者进行分类。然后使用离散小波变换来分析癫痫检测。数据集也被分为训练数据集和测试数据集,以确保在所有情况下都能正确表征。虽然检测算法是用训练数据集开发的,但测试数据集是用来防止过拟合和减少离群点数量的。其他几种算法已经被开发并用于癫痫发作检测,但有些算法存在这样或那样的限制。这关注的不仅仅是算法的开发。这关注的焦点应该是优化和准确的表征,以便能够以尽可能低的错误形式完成癫痫发作检测。
该工作结合了小波域和机器学习的方法来识别癫痫发作。脑电信号具有非线性、非平稳、复杂等特点,对其进行时频分析的方法很多。在本研究中,采用了离散小波变换技术。通过特征提取来提取信号的隐藏特征,这有助于对信号进行检测。这些特征被输入到区分健康和癫痫信号的分类器中,使用的分类器有k近邻、支持向量机、朴素贝叶斯和决策树分类器[15,16]。这些分类器的性能通过统计参数来衡量。
这项工作的其余部分结构如下。第二节介绍了方法。结果和讨论在第三节给出。与其他现有最新发展的比较在第四节给出,结论在第五节给出。
2. Methods
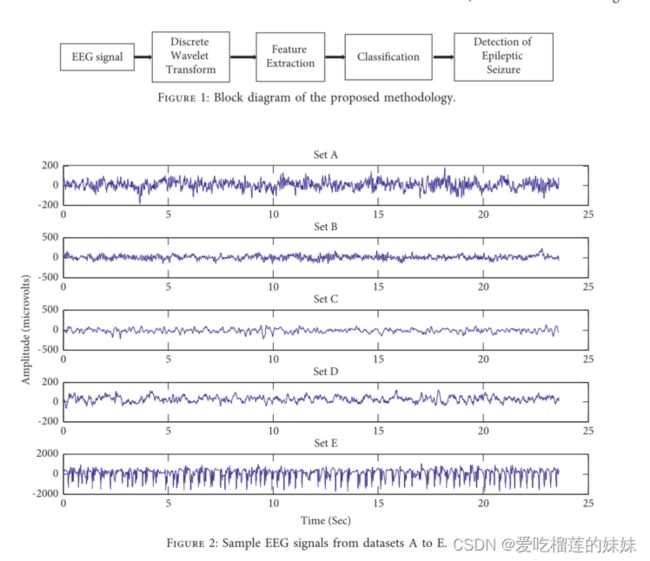
利用离散小波变换将脑电数据分割成6个频率子带。基本特征,如平均功率、最小系数、最小频段、最小频段。均值和最高系数被去除并输入到NAıve Bayes、支持向量机、决策树分类器和KNN中。对每个分类器和特征进行计算。提出的框架如图1所示。
2.1.波恩大学数据集。
数据可在德国波恩大学癫痫学系的网站上获得[15]。这是专门为研究目的提供的单通道数据。记录包含五个数据集,命名为集合A到集合E。每组数据有100个样本。通过单通道记录在头部表面的100个脑电片段所需的时间为23.6s。5名健康志愿者被选为A和B组,分别记录脑电信号并进行仔细观察。对于C组,患者在半球海马区没有癫痫发作,而对于D组,致痫区是记录发生的地方。记录患者癫痫发作时的E组脑电信号。使用采样频率为173.61 Hz的12位A/D转换器对数据进行数字化。因此,每个脑电片段被发现包含4096个采样点。图2中绘制了脑电信号图。
2.2.实时临床数据集。
实时多通道临床数据来自印度泰米尔纳德邦埃罗德的Senthil综合专科医院的6名健康患者和6名癫痫患者。数据为21导联脑电数据,在潜伏期记录癫痫信号,采样频率保持在2 5 6 Hz。
2.3.利用离散小波变换对信号进行预处理。
频域分析的快速傅立叶变换(FFT)在许多应用中得到了应用。但是,对于脑电信号这样的生物医学信号,FFT的使用受到了限制,因为它们包含不均匀的模式,而且是非平稳的,仅靠时域分析不能得到关于模式频率的信息,因此应用时频分析对信号进行预处理。 是一种广泛应用于生物医学信号的时频分析方法,它喜欢可变窗口大小。离散小波变换算法使用低通和高通的正交镜像滤波器。
输入信号通过低通和高通滤波器来产生近似(A1)系数和它们的输出细节(D1)系数。从高通滤波器得到的结果被提供给另一个正交镜像型的滤波器,并且重复该过程以确定后续电平的系数。每一次分解过程都会导致频率分辨率因滤波而加倍,而通过下采样使频率分辨率减半。
由于Daubechies四阶小波函数的正交性和滤波效率,采用Daubechies四阶小波函数,从子带频率中提取所需的统计特征。
2.4.离散小波变换(DWT)系数的统计特征。
提取了以下特征。
平均值(MAV)。MAV与信号的信息频率有关,可通过以下公式确定
最大系数,测量给定样本的最大频率值。
最小系数,测量给定样本的最小频率值。
标准差(STD)。标准偏差与频率信号的比例变化有关,由以下公式给出:
平均功率(AVP),平均功率表示有关信号的频率内容的信息,并由以下公式确定:
香农熵(SE),香农熵的表达式提供了一种简单的方式来确定编码一串符号所需的平均比特数。它由以下等式给出:
近似熵(ApEn),时间序列数据波动的规律性和不可预测性的程度可以用近似熵(m,r,N)来量化。参数m和r分别是游程长度和公差窗口输入参数。参数N是时间序列的点数。
2.5. K-Fold Cross-Validation.
10倍交叉验证,在本研究中使用,以获得可靠的结果。将原始样本分为10个子样本, 9个子样本作为训练数据集,1个子样本作为测试数据集。然后重复10次。通过这种方式,每个数据集被训练9次,并测试一次。然后对获得的10结果进行平均,以给出单一的估计精度。将有效性应用于支持向量机、KNN、朴素贝叶斯和决策树分类器。
2.6. Support Vector Machine (SVM) Classifier. 支持向量机(SVM)分类器。
支持向量机是一种基于机器学习算法的二分类器模型。在这种格式中,训练数据集被分为两组,以便划分尽可能宽。机器学习[46]算法生成超平面图,该图使用训练数据集来分布这两组。从曲线图中,如果超平面离数据较近,则认为该数据集不敏感。选择离数据点最远的最优超平面。使用最优超平面对测试数据集进行分类。
超平面的方程是f(x)=β0+βtx,(5)其中 β 是权向量,β0 是偏置向量。通过改变这两个参数,可以获得无限数量的超平面。最优超平面的条件是 β0+βtx =1,(6)其中x表示支持向量,即最接近超平面的训练集。
2.7. k-Nearest Neighbor (kNN) Classifier.k-最近邻分类器。
kNN是非参数非线性分类器。它用于相对较大的训练集。训练集和测试集[47]之间的相似性被考虑用于测量。在附近的“k”个数据集中占多数的类被分配给测试/未知数据集。数据集的“接近度”是使用欧几里德距离来测量的,该距离由下式给出
其中Y1i(y11,y12,.。。y1n)和Y2i’(y21,y22,.。。,y2n)。
k的值应该是正整数。在本研究中,k值为3。
2.8.朴素贝叶斯分类器。
分类器基于贝叶斯理论,是一种概率分类器。它还基于这样一个假设,即每个类特性独立于任何其他特性。NB分类器需要较少的训练数据。
假设D为n个类的训练集,Y为属性向量和相关的类标签,属性Y所属的具有最高后验概率的类由下式给出
这里P(Ci)表示类别概率,P(Y)是Y的先验概率,P(Ci|Y)是后验概率,P(Y|Ci)是以Ci为条件的Y的后验概率。
2.9. Decision Tree (DT) Classifier. 决策树分类器
DT是一种广泛用于数据挖掘、统计和机器学习算法的预测建模方法。在目标变量被赋予连续值的情况下,使用树模型。决策树的树叶代表类别标签,树枝代表导致这些类别标签的特征的组合。
2.10. Statistical Parameter.统计参数
使用六个参数评估四个分类器的性能,即准确性、特异性、敏感性、正预测值(PPV)、负性预测值(NPV)和马修斯相关系数(MCC) [4,5]。参数的数学定义如下:
其中,CCP表示正确的分类模式,而总模式表示为TPT。Tp表示真阳性,Fn表示假阴性,FP表示假阳性,Tn表示真阴性。
3. Results and Discussions
3.1. Results from the University of Bonn Dataset
来自集合A、B、C、D和E的数据集被分解到不同的6个子带中。不同频率子带分别为:d1(43.4~86.8 hz)、d2(21.7~43.4 hz)、d3(10.85~21.7 hz)、d4(5.42~10.85 hz)、d5(2.70~5.43 hz)和a5(0~2.70 hz)。
由于最有用的信息在子带D3-D5和A5中可用,因此只考虑它们[10]。从五个数据集A、B、C、D和E的子带D3、D4、D5和A5中导出诸如平均绝对值、最大系数、最小系数、标准差、平均功率、香农熵和近似熵等特征。
考虑了16个案例,其中包括2个类别分类和3个类别分类,这些分类基于德国波恩大学现成的数据。在研究中获得了7个特征。然而,为每个脑电信号生成的特征的数量应该是4x7=28。对于数据集A到E的每100个信号,生成28个特征。在每种情况下,都应用了10次交叉验证,将整个数据分为10个相等的部分,其中9个数据部分用于训练,而1个数据部分用于测试目的。然后,将支持向量机、KNN、朴素贝叶斯和决策树分类器输入以下训练和测试集,并获得诸如准确度、特异度、灵敏度、正预测值、负预测值和马修斯相关系数等性能指标。
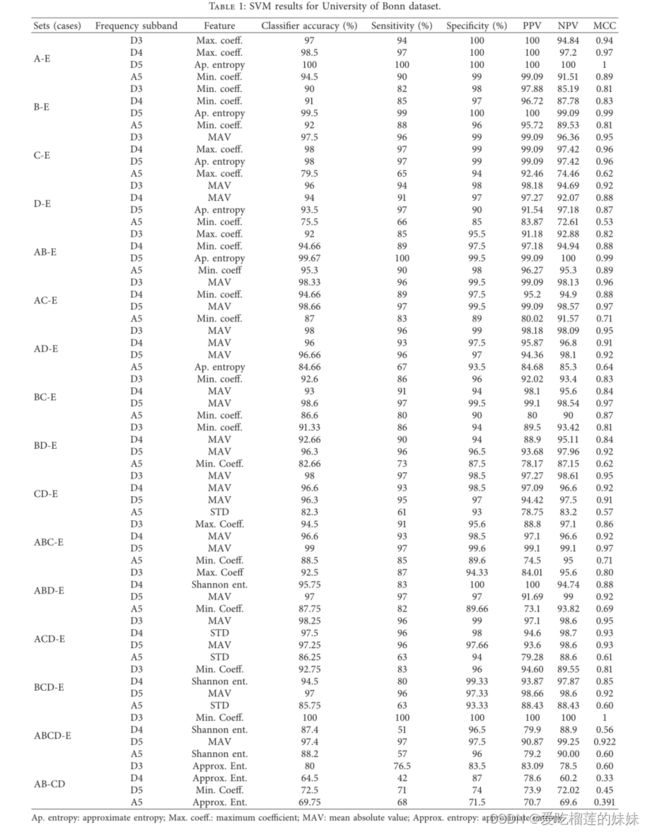
从表1中,我们可以观察到SVM分类器的16种不同分类的结果。对于A-E分类,从D5频率子带估计的熵可提供100%的最高精度。类似地,对于B-E分类,从D3、D4和A5频率子带中提取的最小系数分别只有90%、91%和92%的准确率,但从D5频率子带中提取的近似熵的准确率最高,为99.5%。对于C-E分类,在D4频率子带,最大系数的准确率最高,为98%。对于D-E分类,在D3频段,MAV的准确率最高,为96%。对于AB-E分类,在D5频率子带中,近似熵的准确率最高,达到99.67%。对于AC-E分类,在D5频段,MAV的准确率最高,达到98.66%。对于AD-E分类,在D3频率子带中,MAV提供了98%的最高精度。对于BC-E分类,在D3频率子带,最小系数为92.6%。对于BD-E分类,在D5频段,MAV的准确率最高,达到96.3%。对于CD-E分类,在D3频段,MAV的准确率最高,达到98%。对于ABC-E分类,在D5频段,MAV的准确率最高,达到99%。对于ABD-E分类,在D5频段,MAV的准确率最高,达到97%。对于ACD-E分类,在D3频段,MAV的准确率最高,为98.25%。对于BCD-E,在D5频率子带中,MAV给出了97%的最高精度。对于ABCD-E分类,在D3频段内,系数最小时,准确率为100%。对于AB-CD分类,在D3频率子带,近似熵给出了80%的精度。此外,我们可以推断,能提供SVM最佳结果的特征是Mean Absolute Value。 A-E和ABCD-E分类的准确率最高,为100%。AB-CD分类达到了最低的分类精度。
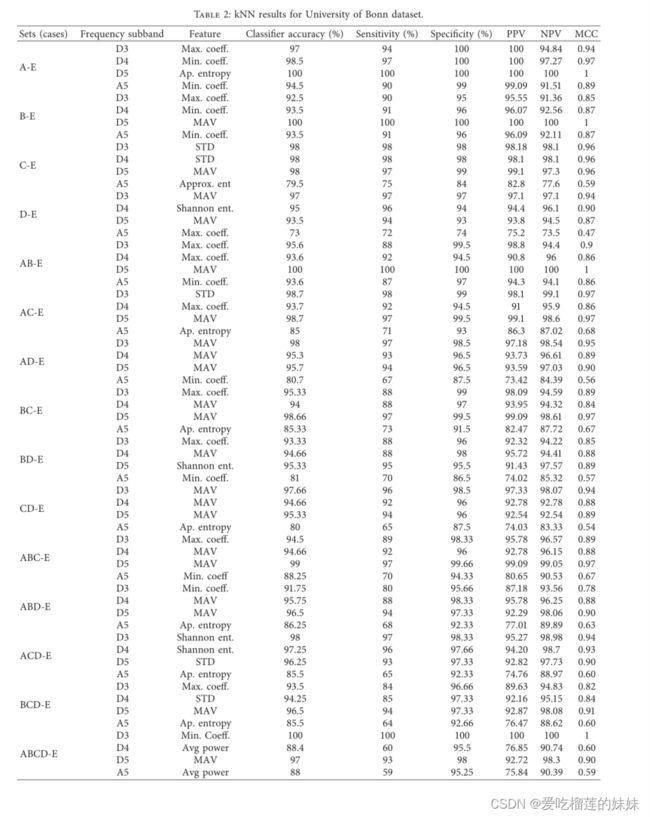
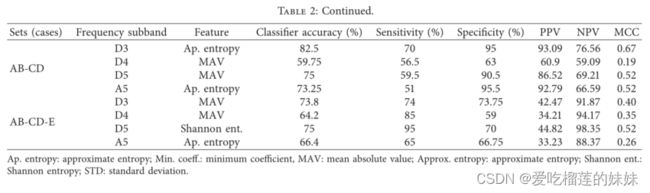
从表2中,我们可以观察到kNN分类器的17种不同分类的结果。对于A-E分类,来自D5频率子带的近似熵给出了100%的最高精度。B-E分类中,从D3、D4、A5频段提取的最大最小系数效果较差,而从D5频段提取的MAV效果最好,为100%。在C-E分类中,在D3、D4和D5频段中,STD的准确率最高,达到98%;在A5频段中,ApEp的准确率达到79.5%。对于D-E分类,在D3频段子波段,MAV的最佳准确率为97%。对于AB-E分类,在D5频率子带中,MAV的准确率最高,为100%。对于AC-E分类,在D3频段,STD的准确率最高,达到98.7%。对于AD-E分类,在D3频段,MAV的准确率最高,达到98%。对于BC-E分类,在D5频带中,MAV有较好的结果。㼿e A-E, B-E, AB-E和ABCD-E分类的最高准确率是100%。㼿e AB-CD和AB-CD- e分类精度最低,准确率最高,为98.6%。对于BD-E分类,在D5频率子带,Shannon熵的准确率最高,达到95.33%。对于CD-E分类,在D3频段,MAV的准确率最高,达到97.66%。对于ABC-E分类,在D5频段,MAV的准确率最高,达到99%。对于ABD-E分类,在D5频段,MAV的准确率最高,达到96.5%。对于ACD-E分类,在D3频率子带,香农熵提供了98%的最高精度水平。对于BCD-E分类,在D5频率子带中,MAV提供了最高水平的97%的准确性。对于ABCD-E分类,在D3频段内,系数最小时,准确率为100%。对于AB-CD分类,在D5频段内,MAV的最佳准确率为75%。对于AB-CD-E分类,在D5频段,Shannon熵的最佳准确率为75%。此外,我们可以推断,平均绝对值和香农熵是kNN提供最佳结果的特征。
从表3中,我们可以观察到na¨avve贝叶斯分类器的16种不同分类的结果。对于A-E分类,来自D5频率子带的MAV给出了100%的最高精度。在B-E分类中,D3提取的最小系数、D4提取的平均功率和A5频率子带提取的ApEp效果较差。从D5中提取MAV的效果最好,可达99.5%。对于C-E分类,在D3、D4、D5和A5频率子带中提取了STD,只有在D5频率子带中达到了100%的最高精度。对于D-E分类,在D3频段内,MAV的准确率最高,为97.5%。对于AB-E分类,在D5频率子带中,STD的准确率最高,达到99.7%。对于AC-E分类,在D3频率子带中,STD提供了最高的精度水平,达到98.7%。对于AD-E分类,在D3频率子带中,MAV提供了98%的最高精度。对于BC-E分类,在D5频率子带,近似熵提供98.7%的最高准确度。对于BD-E分类,在D5频率子带中,ApEp给出了96%的最大准确度。对于CD-E分类,在D3和D4频率子带中,MAV给出了97.7%的最大准确度。对于ABC-E分类,在D5频率子带中,MAV给出了99%的最大准确度。对于ABD-E分类,在D5频率子带中,ApEp给出了96.25%的最大准确度。对于ACD-E分类,在D5频率子带中,ApEp给出了97.6%的最大准确度。对于ABCD-E分类,在D3频率子带中,最小系数给出了97.4%的最佳准确度。对于AB-CD分类,在D3频率子带中,近似熵给出了82.5%的最大准确度。此外,从表3中,我们可以推断出显示朴素贝叶斯最佳结果的属性是平均绝对值和近似熵。对于A-E和C-E,最大准确度达到100%。AB-CD分类达到最低准确度。
从表4中,我们可以观察到决策树分类器的16个不同分类的结果。对于A-E分类,来自D5频率子带的MAV给出100%的最高准确度。对于B-E分类,从D3提取的最大系数和从A5频率子带提取的D4和STD给出差的结果,但是从D5提取的MAV给出100%的最好结果。对于汉英分类,从D4提取的香农熵给出了最高的准确率98。对于D-E分类,在D3频率子带中,MAV给出了96.5%的最佳准确度。
对于AB-E分类,在D5频率子带中,MAV给出了100%的最大准确度。对于AC-E分类,在D3频率子带中,STD提供了98.67%的最高准确度。在D5频率子带中,ApEp提供了98.67%的最高准确度。对于AD-E分类,在D3频率子带中,MAV提供了98%的最高准确度。对于BC-E分类,在D5频率子带中,MAV提供了98.33%的最高水平的准确度。对于BD-E分类,在D5频率子带中,MAV提供了94.67%的最高水平的准确度。对于CD-E分类,在D3频率子带中,MAV提供了96.67%的最高水平的准确度。对于ABC-E分类,在D3频率子带中,最小系数给出94.5%的最佳准确度。对于ABD-E分类,在D4频率子带中,最大系数给出了95.75%的最高准确度。对于ACD-E分类,在D3频率子带中,MAV给出了98%的最大准确度。对于BCD-E分类,在D5频率子带中,ApEp给出了96.25%的最大准确度。对于ABCD-E分类,在D3频率子带中,最小系数给出100%的最佳准确度。对于AB-CD分类,在D3频率子带中,MAV给出的最大准确率为79.75%。此外,我们可以推断,显示决策树的最佳结果的属性是平均绝对值和香农熵。对于A-E、B-E、AB-E和ABCDE分类,㼿e达到了100%的最高准确度。㼿e最低分类为AB-CD分类。
3.2. Results from Clinical Real-Time Dataset.来自临床实时数据集的结果。
来自健康信号的实时临床数据集区别于癫痫患者信号。我们已经应用了DWT并为不同的子带生成了特征。工作考虑了24秒内获得的所有21通道数据集。特征由子带D3–D5和A5产生,这些特征用于分类[15,16,18]。
但是仅对于使用SVM分类器从D5子带导出的平均功率特征获得了更好的结果。表5显示了结果。这里,我们对分类应用了10重交叉验证,因为大多数有用的区分健康和癫痫患者信号所需的信息[48]可能在子带D5中。
4. Comparison with Existing State of the Art与现有技术水平的比较
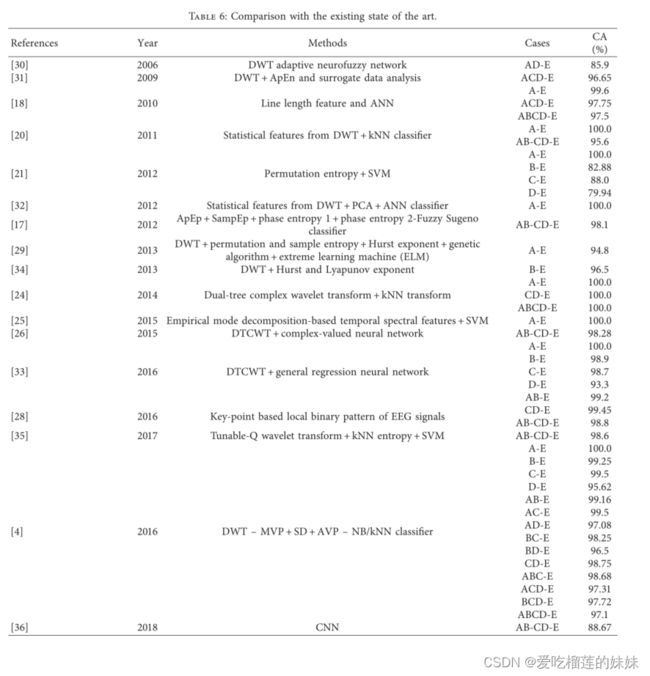
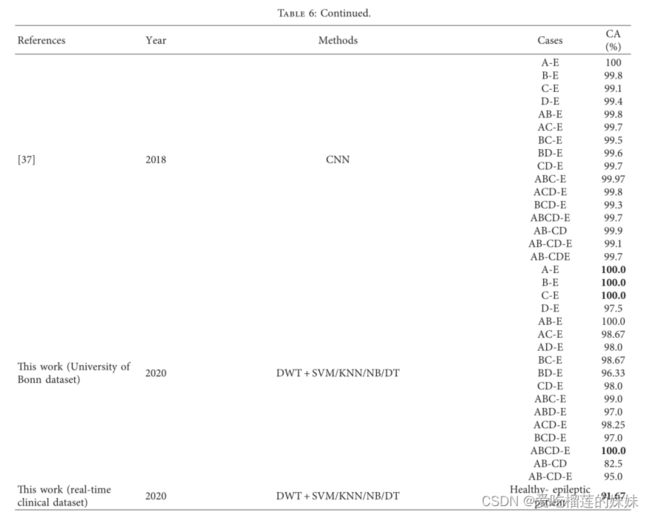
不同的研究人员提出了几种从EEG信号中检测癫痫发作的技术。他们的工作与本工作进行了比较,并在表6中列出。显示了使用相同数据集的方法进行比较。已经注意到,诸如DTCWT、经验模式分解、CNN和模糊神经网络之类的几种策略被用于检查EEG以从正常情况中识别癫痫发作。
大多数研究人员将集合a与集合e进行二级分类,得到了94.8%到100%的分类准确率[19–31,39–42]。许多研究人员也用集合E对集合B进行分类,分类准确率从82.88%到99.25% [19,25,29,31,41]。在用集合E对集合C进行分类时,研究人员获得了从88%到99.6%的分类准确率[23,25,29,31,41]。对于集合D与集合E的分类,研究人员得到的分类准确率从79.94%到95.85% [23,25,29,31,41]。我们在工作中也实现了100%的A-E分类。对于B-E、C-E和D-E分类,我们得到了更好的结果。我们实现了100%的B-E分类准确率,而迄今为止的最高准确率仅为99.25%。同样,对于C-E分类,我们达到了100%的准确率,而迄今为止的最高准确率仅为99.6%。我们已经实现了97.5%的D-E分类,但是迄今为止实现的最大准确度是95.85%。
研究人员还合并了从集合A到集合D的两个数据集,并用集合E对它们进行分类,在AB-E分类的情况下,迄今为止达到的最大精度为99.2% [29]。在我们的工作中,我们达到了100%的准确率。对于AC-E分类,我们的准确率为98.6%,但达到的最大准确率为99.5% [23]。对于AD-E分类,研究者得到了85.9% [30]和97.08% [29]的分类准确率,但我们得到了更好的98%的准确率。研究人员获得了98.25%的分类准确率[31],但我们获得了更好的98.67%的准确率。在BD-E分类的情况下,我们得到了96.33%的分类准确度,但是所达到的最大准确度已经是96.5% [28]。
类似地,对于CD-E分类,我们得到了98%的分类准确度,但是达到的最大准确度是100% [26]。同样,研究人员组合了三个不同的数据集,并用set E对它们进行分类。研究人员对ABC-E实现了98.68% [31]的分类准确率,但我们在工作中实现了更好的99%的准确率。对于ACD-E分类,研究人员已经实现了从96.65%到98.15%的分类准确率[20,25,31,34]。在我们的工作中,我们取得了稍好的98.25%的准确率。我们还对ABD-E进行了分类,这在以前的任何工作中都没有计算过,并且达到了97%的准确率。对于BCD-E分类,我们已经实现了97%的分类准确度,但是最高准确度已经达到97.72% [31]。
其他两类分类是ABCD-E和ABCD。对于ABCD-E分类,我们的结果与其他研究者的结果相当。研究人员已经实现了从97.1% [28]到100% [26]的准确率。在我们的工作中,我们也达到了100%的准确率。此外,我们将集合A与集合B以及集合C与集合D进行了组合,并对这两个组合数据集进行了分类。以前没有尝试过㼿is类型的分类,我们获得了82.5%的分类准确度。
此外,对于三级分类AB-CD-E,研究人员已经实现了95.6%至98.8%的分类准确率[22,28,31,35,36]。在我们的工作中,只有95%的准确率。
已经进行了许多关于将集成技术应用于科学和工程的各个方面的研究。集成模型将几个基本模型结合起来,以获得具有高预测能力的整体模型。[5,43–45]中提供了用于科学和工程各个领域的集合模型。
4.1. Discussion of Key Findings.讨论关键发现。
对于A-E分类,从D5频率子带提取的MAV、STD和平均功率被馈送到kNN、NB和DT分类器,给出100%准确度的最佳结果。 SVM分类器对于来自D5频率子带的近似熵特征给出100%的准确度。对于B-E分类,从D5频率子带取出的MAV、STD和平均功率被馈送到kNN和DT分类器,这给出了100%准确度的最佳结果。对于C-E分类,从D3频率子带提取的STD和平均功率被馈送到NB分类器,给出100%准确度的最佳结果。对于D-E分类,从D3频率子带提取的MAV被馈送到NB分类器,这给出了97.5%准确度的最佳结果。对于AB-E分类,从D5频率子带提取的MAV和香农熵被馈送到kNN和DT分类器,给出100%准确度的最佳准确度结果。对于AC-E分类,从D3和D5频率子带提取的STD被馈送到kNN和DT分类器,给出98.67%准确度的最佳结果。对于AD-E分类,从D3频率子带提取的MAV被馈送到所有分类器,给出98%准确度的最佳结果。对于BC-E分类,从D5频率子带提取的MAV被馈送到kNN、NB和DT分类器,给出98.67%准确率的最佳结果。
对于BD-E分类,从D5频率子带提取的MAV被馈送到SVM分类器,给出96.33%准确度的最佳结果。对于CD-E分类,从D3频率子带提取的MAV被馈送到SVM分类器,给出98%准确度的最佳结果。对于ABC-E分类,从D5频率子带提取的MAV被馈送到SVM、kNN和NB分类器,这给出了99%准确度的最佳结果。对于ABD-E分类,从D5频率子带提取的MAV被馈送到SVM分类器,这给出了97%准确度的最佳结果。对于ACD-E分类,从D3频率子带提取的MAV被馈送到SVM和NB分类器,给出98.25%准确度的最佳结果。对于BCD-E分类,从D5频率子带提取的MAV被馈送到SVM和NB分类器,这给出了97%准确度的最佳结果。对于ABCD-E分类,从D5频率子带提取的最小系数被馈送到SVM、kNN和DT分类器,给出100%准确度的最佳结果。对于AB-CD分类,从D3频率子带提取的ApEp被馈送到kNN和NB分类器,这给出了82.5%准确度的最佳结果。
对于AB-CD-E分类,来自D5频率子带的香农熵被馈送到kNN分类器,这给出了95%准确度的最佳结果。从表6中,我们可以得出结论,我们已经实现了A-E、B-E、C-E、AB-E和ABCD-E分类的100%的准确性,这是以前已经实现的。此外,在癫痫发作的检测中,我们对DE、BC-E和ABC-E的数据集组合实现了更好的准确性。
5. Conclusions
本文提出了一种利用时频域特征和多种分类器识别癫痫发作的新方法。德国波恩大学开发的数据集达到了100%的最高分类率。从印度Senthil多专科医院的实时数据中获得了91.67%的总体准确率。它提出的方法是成功的,经过验证,并与现有的几个文献中的现有方法的准确性进行比较。工作还提出了不同的基本分类器机器学习模型,以表征EEG信号并准确检测癫痫发作。这项工作的重要贡献之一是如果在数据集上提供广泛的机器学习模型,所提出的方法可以保证准确的预测。相比之下,其他现有的关于EEG信号的工作并没有检查这项工作中探索的那么多模型。检查不同的基本分类器模型对于泛化是至关重要的。它是本文的优势和关键贡献之一。由于我们可以在临床上测试结果的有效性,我们将在未来的工作中进一步开发该算法,以便在医院中实施。