蓝桥杯刷题五

1.01背包问题

这题就是01背包问题的模板题 回顾一下01背包 01就是这个东西选和不选

01背包的表达式是f[i]=max(f[i-v]+w,f[i]);

那么这题就可以直接做了 值得注意的是这里只用了一维数组 所以更新的时候要从后往前面更新

#include 
using namespace std;
const int N=1e3+10;
int f[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=0;i>v>>w;
        for(int j=m;j>=v;j--)
        {
            f[j]=max(f[j],f[j-v]+w);
        }
    }
    cout<

2.摘花生

这题是简单的线性dp，分析一下假定起点为f[1][1],终点是f[n][m] 并且每次都只能东走或者往南走(这句话就是决定了本题没有任何的循环依赖),所以可以用dp做f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j]

#include 
using namespace std;
const int N=110;
int f[N][N];
int a[N][N];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        memset(f,0,sizeof f);
        memset(a,0,sizeof a);
        int r,c;
        cin>>r>>c;
        for(int i=1;i<=r;i++)
            for(int j=1;j<=c;j++)
                cin>>a[i][j];
        for(int i=1;i<=r;i++)
            for(int j=1;j<=c;j++)
                f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];
        cout<

3.最长上升子序列

这也是很经典的线性dp。定义f[i]是以i为结尾的最长上升子序列，那我们去找在他前面的比它小的，并且去比较是f[i]大 还是f[j]+1 大 这样递归去求 就可以做了

注意 要把f[i]定义为1先 这是具体含义决定的

#include 

using namespace std;

const int N = 1010;

int res, a[N], f[N];

int main() {
    int n;  cin >> a[i];

    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
    }

    for (int i = 1; i <= n; i ++) {
        f[i] = 1;
        for (int j = 1; j < i; j ++) {
            if (a[i] > a[j]) {
                f[i] = max(f[i], f[j] + 1);
            }
        }

        res = max(res, f[i]);
    }

    return cout << res << '\n', 0;
}

4.地宫取宝

这个很像递归,

递归怎么递归呢

当走到某个格子上的时候：

（1）如果格子上宝贝的价值大于已有宝贝的最大值，那么可以选择拿或者不拿

（2）如果格子上宝贝的价值小于或者等于已有宝贝的最大值，那么只能选择不拿。

必须从左上角走到右下角，且只要到达右下角时物品个数满足条件即算一种方案。

只能选择向下或者向右走

不是必须到出口时，宝贝数量恰好满足条件，而是可以在任意位置就宝贝数量就可以满足条件，只需保证到达出口时宝贝数量仍然满足条件即可

#include 
using namespace std;
const int N=15;
int w[N][N];
int n,m;
int k;
int maxl=-0x3f3f3f3f;
const int mod=1000000007;
int dfs(int x,int y,int step,int Max)
{
    if(x>n||y>m||step>k) return 0;
    if(x==n&&y==m)
    {
        if(step==k||(w[x][y]>Max&&step+1==k))
            return 1;
        else return 0;
    }
    if(w[x][y]>Max)
    {
        return dfs(x,y+1,step+1,w[x][y])+
        dfs(x,y+1,step,Max)+
        dfs(x+1,y,step+1,w[x][y])+
        dfs(x+1,y,step,Max);
    }
    else return dfs(x,y+1,step,Max)+dfs(x+1,y,step,Max);
}
int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>w[i][j];
    cout<

递归就超时了，所以要想别的办法 这题和摘花生有点像，那么应该是dp

那么就得用dp了 并且要用四维的dp去做x y step Max

由于宝贝的价值可以为0，因此一开始所持有0件宝贝，价值为-1，-1无法索引，为了便于在表中表示，我们将所有宝贝的价值都+1

递归改的代码在这里https://www.acwing.com/solution/content/34645/

初始化状态

#include 
#include 
#include 

using namespace std;

const int N = 55, MOD = 1000000007;

int n, m, k;
int w[N][N];
int f[N][N][13][14];

int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            cin >> w[i][j];
            w[i][j] ++ ;
        }

    f[1][1][1][w[1][1]] = 1;
    f[1][1][0][0] = 1;

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            if (i == 1 && j == 1) continue;
            for (int u = 0; u <= k; u ++ )
                for (int v = 0; v <= 13; v ++ )
                {
                    int &val = f[i][j][u][v];
                    val = (val + f[i - 1][j][u][v]) % MOD;
                    val = (val + f[i][j - 1][u][v]) % MOD;
                    if (u > 0 && v == w[i][j])
                    {
                        for (int c = 0; c < v; c ++ )
                        {
                            val = (val + f[i - 1][j][u - 1][c]) % MOD;
                            val = (val + f[i][j - 1][u - 1][c]) % MOD;
                        }
                    }
                }
        }

    int res = 0;
    for (int i = 0; i <= 13; i ++ ) res = (res + f[n][m][k][i]) % MOD;

    cout << res << endl;

    return 0;
}

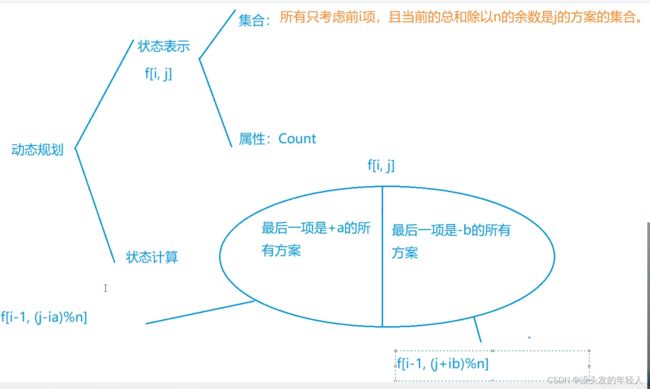
5.波动数列

设第一个数为 x, 第二个数为 x + d1, 第三个数为 x + d[1] + d[2]

第 n 个数为 x + d[1] + d[2] + ... + d[n - 1]; d[i] 的值为 a 或 -b

故数列之和 s = n * x + (n - 1) * d[1] + ... + (n - i) * d[i] + ... + d[n - 1]

x = (s - ((n - 1) * d[1] + ... + (n - i) * d[i] + ... + d[n - 1])) / n

因为 x 为任意整数, 故：

s % n == ((n - 1) * d[1] + ... + (n - i) * d[i] + ... + d[n - 1]) % n

f[0,0]=1

#include 

using namespace std;

const int N = 1010, MOD = 100000007;

int f[N][N];
int get(int x, int y) {  // 返回 x 除 y 的正余数 
    return (x % y + y) % y; 
}

int main() {
    int n, s, a, b;
    cin >> n >> s >> a >> b;

    f[0][0] = 1;
    for (int i = 1; i < n; i ++) {
        for (int j = 0; j < n; j ++) {
            int x = get(j - (n - i) * a, n);
            int y = get(j + (n - i) * b, n);
            f[i][j] = (f[i - 1][x] + f[i - 1][y]) % MOD;
        }
    }

    return cout << f[n - 1][get(s, n)] << '\n', 0;
}