PINN解偏微分方程实例1

1. PINN简介

   PINN是一种利用神经网络求解偏微分方程的方法，其计算流程图如下图所示，这里以偏微分方程(1)为例。
$$\begin{array}{r}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=v\frac{{\partial }^{2}u}{\partial x^2}\end{array}$$
神经网络输入位置x,y,z和时间t的值，预测偏微分方程解u在这个时空条件下的数值解。

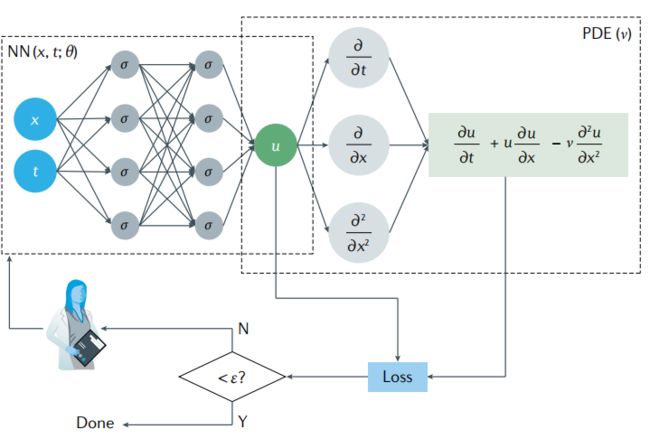
   上图中可以看出，PINN的损失函数包含两部分内容，一部分是来源于训练数据误差，另一部分来源于偏微分方程误差，可以记作(2)式。
$$\begin{array}{r}l=w_{data}{l}_{data}+w_{PDE}{l}_{PDE}\end{array}$$
其中
$$\begin{array}{r}\begin{array}{rl}{l}_{data}& =\frac{1}{N_{data}}\sum _{i=1}^{N_{data}}(u(x_i,t_i)-u_i{)}^2\\ l_{PDE}& =\frac{1}{N_{data}}\sum _{j=1}^{N_{PDE}}{\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}-v\frac{{\partial }^{2}u}{\partial x^2}\right)}^2{|}_{(x_j,t_j)}\end{array}\end{array}$$

2. 偏微分方程实例

   考虑偏微分方程如下：
$$\begin{array}{r}\begin{array}{r}\frac{{\partial }^{2}u}{\partial x^2}-\frac{{\partial }^{4}u}{\partial y^4}=(2-x^2)e^{-y}\end{array}\end{array}$$
考虑以下边界条件，
$$\begin{array}{r}\begin{array}{rl}{u}_{yy}(x,0)& =x^2\\ u_{yy}(x,1)& =\frac{x^2}{e}\\ u(x,0)& =x^2\\ u(x,1)& =\frac{x^2}{e}\\ u(0,y)& =0\\ u(1,y)& =e^{-y}\end{array}\end{array}$$
以上偏微分方程真解为$u(x,y)=x^2{e}^{-y}$,在区域$[0,1]\times [0,1]$上随机采样配置点和数据点，其中配置点用来构造PDE损失函数$l_1,l_2,\cdots ,l_7$，数据点用来构造数据损失函数$l_8$.
$$\begin{array}{r}\begin{array}{rl}{l}_1& =\frac{1}{N_1}\sum _{(x_i,y_i)\in \Omega }({\hat{u}}_{xx}(x_i,y_i;\theta )-{\hat{u}}_{yyyy}(x_i,y_i;\theta )-(2-x_i^2)e^{-y_i}{)}^2\\ l_2& =\frac{1}{N_2}\sum _{(x_i,y_i)\in [0,1]\times \{0\}}({\hat{u}}_{yy}(x_i,y_i;\theta )-x_i^2{)}^2\\ l_3& =\frac{1}{N_3}\sum _{(x_i,y_i)\in [0,1]\times \{1\}}({\hat{u}}_{yy}(x_i,y_i;\theta )-\frac{x_i^2}{e}{)}^2\\ l_4& =\frac{1}{N_4}\sum _{(x_i,y_i)\in [0,1]\times \{0\}}(\hat{u}(x_i,y_i;\theta )-x_i^2{)}^2\\ l_5& =\frac{1}{N_5}\sum _{(x_i,y_i)\in [0,1]\times \{1\}}(\hat{u}(x_i,y_i;\theta )-\frac{x_i^2}{e}{)}^2\\ l_6& =\frac{1}{N_6}\sum _{(x_i,y_i)\in \{0\}\times [0,1]}(\hat{u}(x_i,y_i;\theta )-0{)}^2\\ l_7& =\frac{1}{N_7}\sum _{(x_i,y_i)\in \{1\}\times [0,1]}(\hat{u}(x_i,y_i;\theta )-e^{-y_i}{)}^2\\ l_8& =\frac{1}{N_8}\sum _{i=1}^{N_8}(\hat{u}(x_i,y_i;\theta )-u_i{)}^2\end{array}\end{array}$$

3. 基于pytorch实现代码

"""
A scratch for PINN solving the following PDE
u_xx-u_yyyy=(2-x^2)*exp(-y)
Author: ST
Date: 2023/2/26
"""
import torch
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

epochs = 10000    # 训练代数
h = 100    # 画图网格密度
N = 1000    # 内点配置点数
N1 = 100    # 边界点配置点数
N2 = 1000    # PDE数据点

def setup_seed(seed):
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.deterministic = True

# 设置随机数种子
setup_seed(888888)

# Domain and Sampling
def interior(n=N):
    # 内点
    x = torch.rand(n, 1)
    y = torch.rand(n, 1)
    cond = (2 - x ** 2) * torch.exp(-y)
    return x.requires_grad_(True), y.requires_grad_(True), cond


def down_yy(n=N1):
    # 边界 u_yy(x,0)=x^2
    x = torch.rand(n, 1)
    y = torch.zeros_like(x)
    cond = x ** 2
    return x.requires_grad_(True), y.requires_grad_(True), cond


def up_yy(n=N1):
    # 边界 u_yy(x,1)=x^2/e
    x = torch.rand(n, 1)
    y = torch.ones_like(x)
    cond = x ** 2 / torch.e
    return x.requires_grad_(True), y.requires_grad_(True), cond


def down(n=N1):
    # 边界 u(x,0)=x^2
    x = torch.rand(n, 1)
    y = torch.zeros_like(x)
    cond = x ** 2
    return x.requires_grad_(True), y.requires_grad_(True), cond


def up(n=N1):
    # 边界 u(x,1)=x^2/e
    x = torch.rand(n, 1)
    y = torch.ones_like(x)
    cond = x ** 2 / torch.e
    return x.requires_grad_(True), y.requires_grad_(True), cond


def left(n=N1):
    # 边界 u(0,y)=0
    y = torch.rand(n, 1)
    x = torch.zeros_like(y)
    cond = torch.zeros_like(x)
    return x.requires_grad_(True), y.requires_grad_(True), cond


def right(n=N1):
    # 边界 u(1,y)=e^(-y)
    y = torch.rand(n, 1)
    x = torch.ones_like(y)
    cond = torch.exp(-y)
    return x.requires_grad_(True), y.requires_grad_(True), cond

def data_interior(n=N2):
    # 内点
    x = torch.rand(n, 1)
    y = torch.rand(n, 1)
    cond = (x ** 2) * torch.exp(-y)
    return x.requires_grad_(True), y.requires_grad_(True), cond


# Neural Network
class MLP(torch.nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.net = torch.nn.Sequential(
            torch.nn.Linear(2, 32),
            torch.nn.Tanh(),
            torch.nn.Linear(32, 32),
            torch.nn.Tanh(),
            torch.nn.Linear(32, 32),
            torch.nn.Tanh(),
            torch.nn.Linear(32, 32),
            torch.nn.Tanh(),
            torch.nn.Linear(32, 1)
        )

    def forward(self, x):
        return self.net(x)


# Loss
loss = torch.nn.MSELoss()


def gradients(u, x, order=1):
    if order == 1:
        return torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u),
                                   create_graph=True,
                                   only_inputs=True, )[0]
    else:
        return gradients(gradients(u, x), x, order=order - 1)

# 以下7个损失是PDE损失
def l_interior(u):
    # 损失函数L1
    x, y, cond = interior()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(gradients(uxy, x, 2) - gradients(uxy, y, 4), cond)


def l_down_yy(u):
    # 损失函数L2
    x, y, cond = down_yy()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(gradients(uxy, y, 2), cond)


def l_up_yy(u):
    # 损失函数L3
    x, y, cond = up_yy()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(gradients(uxy, y, 2), cond)


def l_down(u):
    # 损失函数L4
    x, y, cond = down()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(uxy, cond)


def l_up(u):
    # 损失函数L5
    x, y, cond = up()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(uxy, cond)


def l_left(u):
    # 损失函数L6
    x, y, cond = left()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(uxy, cond)


def l_right(u):
    # 损失函数L7
    x, y, cond = right()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(uxy, cond)

# 构造数据损失
def l_data(u):
    # 损失函数L8
    x, y, cond = data_interior()
    uxy = u(torch.cat([x, y], dim=1))
    return loss(uxy, cond)


# Training

u = MLP()
opt = torch.optim.Adam(params=u.parameters())

for i in range(epochs):
    opt.zero_grad()
    l = l_interior(u) \
        + l_up_yy(u) \
        + l_down_yy(u) \
        + l_up(u) \
        + l_down(u) \
        + l_left(u) \
        + l_right(u) \
        + l_data(u)
    l.backward()
    opt.step()
    if i % 100 == 0:
        print(i)

# Inference
xc = torch.linspace(0, 1, h)
xm, ym = torch.meshgrid(xc, xc)
xx = xm.reshape(-1, 1)
yy = ym.reshape(-1, 1)
xy = torch.cat([xx, yy], dim=1)
u_pred = u(xy)
u_real = xx * xx * torch.exp(-yy)
u_error = torch.abs(u_pred-u_real)
u_pred_fig = u_pred.reshape(h,h)
u_real_fig = u_real.reshape(h,h)
u_error_fig = u_error.reshape(h,h)
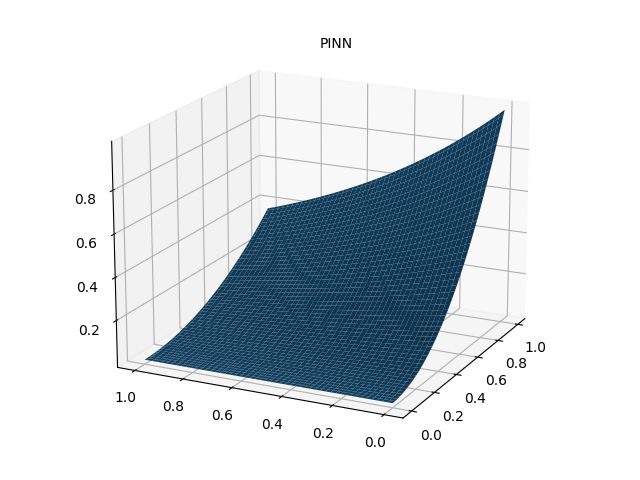
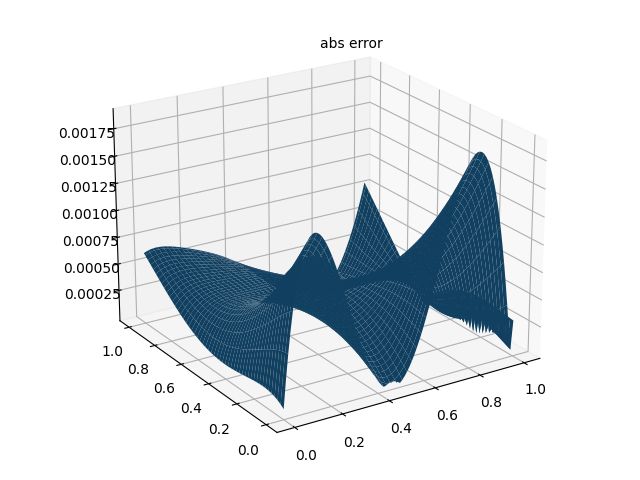
print("Max abs error is: ", float(torch.max(torch.abs(u_pred - xx * xx * torch.exp(-yy)))))
# 仅有PDE损失    Max abs error:  0.004852950572967529
# 带有数据点损失  Max abs error:  0.0018916130065917969

# 作PINN数值解图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xm.detach().numpy(), ym.detach().numpy(), u_pred_fig.detach().numpy())
ax.text2D(0.5, 0.9, "PINN", transform=ax.transAxes)
plt.show()
fig.savefig("PINN solve.png")

# 作真解图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xm.detach().numpy(), ym.detach().numpy(), u_real_fig.detach().numpy())
ax.text2D(0.5, 0.9, "real solve", transform=ax.transAxes)
plt.show()
fig.savefig("real solve.png")

# 误差图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xm.detach().numpy(), ym.detach().numpy(), u_error_fig.detach().numpy())
ax.text2D(0.5, 0.9, "abs error", transform=ax.transAxes)
plt.show()
fig.savefig("abs error.png")

4. 数值解

参考资料

[1]. Physics-informed machine learning
[2]. 知乎-PaperWeekly