图数据库基础知识(下)
目录:
什么是 K-Hop?
K-Hop如何计算?
什么是图算法?
什么是图查询语言?
什么是K-hop?
K-hop的中文的直译为K-跳,也可以被意译为K邻。在图上面,所谓K邻操作,指的是从某个顶点出发,寻找到所有的与其最短路径为K跳(或K步)的顶点的集合。K值为正整数>=1。
在图数据集上面,还有一个概念是图的直径,它的定义是图上的所有顶点间的最大(最长)的最短路径既是图的直径。这个直径的概念实际上就是K值的上限。
例如6度分隔假说中如果把全世界的人放在一张图谱(图数据集)中,任何2个人都可以在六步之内找到他们的关联路径(最短路径),实际上说的就是这张图谱的直径最大为6!同样,可以推导出在这张图中,从任一
顶点出发进行7-Hop计算时,将不会返回任何顶点。
K-Hop如何计算?
我们如果用递归的思路去看K-hop的计算方式。
Step1:
先从1-Hop开始,需要获取当前出发顶点的全部直接关联的邻居,既1度邻居集合;Step2:
再从全部的1度邻居集合中的每个邻居出发,寻找它们各自的全部1度邻居,但是不包含之前已经覆盖过的邻居(例如出发顶点、当前顶点自身或任何在前一层已经搜索过的邻居);Step3:
依照判断是否已经抵达K层,如已抵达,统计并去重后,返回全部当前层的邻居;如未到达第K层,判断是否结果为空,如为空,则立即返回;如果结果不为空,继续进入下一层搜索,逻辑同上。
K-hop计算中,有几个要点非常关键,也特别容易导致操作结果错误,事实上,市面上多款图数据库产品的K-hop的计算结果是错误的。主要有3点:
1.未通过BFS的方式计算K-Hop
2.计算结果应去重,且每一跳没有进行去重操作
3.K-hop限定了搜索数量
关于第一点,如果通过DFS来计算就直接违背了普通最短路径通过BFS来计算的原则,或者说需要遍历全部可能的路径后再去重(例如通过DFS获得任何一条深度为K的路径,需要判别其第K个顶点距离初始顶点的最短路径是K才是正确的结果)才可能得到正确的K-hop结果集。
关于第三点,限定K-Hop的搜索数量这个操作本身与K-hop的定义冲突。例如在腾讯星图SKG中因存在无法全量加载数据的问题,而导致需要限定返回顶点数量,这直接导致了结果集错误。因为如果K-hop不能全量加载,那么K-1 Hop,K-2 Hop可能也会涉及无法全量加载的问题,这种结果错误是有传导效应的、递归式的错误的。
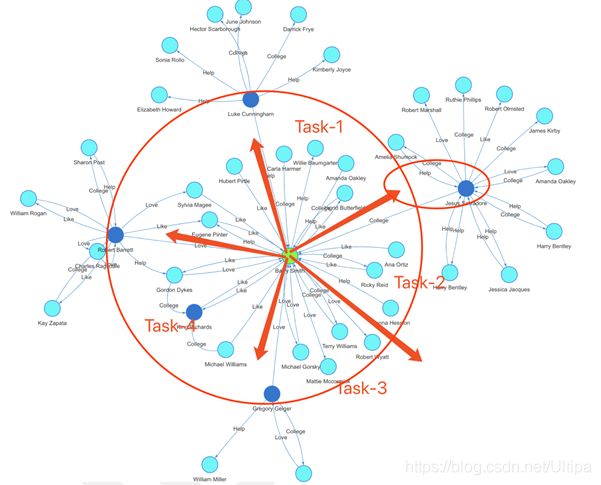
上图中的绿色顶点为起始顶点,从其出发的1-Hop为所有与之直接相连的顶点集合(图上标红的大圆圈与右侧的小椭圆内的所有顶点),而2-Hop的结果集则是以上两个圆之外的所有顶点的集合。关于去重,留意上图中Task-4上方的蓝色顶点King Richards,它本身是属于绿色顶点Barry Smith的1-Hop的,但是如果从他的两个邻居Michael Williams和Gordon Dykes(分别为Barry Smith的1-Hop邻居)出发也可以抵达King Richards,有的图数据库系统就会错误的把它算作2-Hop的顶点。造成这种错误的原因就是因为没有去重,不仅要对最短路径进行判断,还有对边进行去重,例如Gordon Dykes与Barry Smith有两条边直联,但是作为后者的1-Hop顶点,Gordon Dykes应该只被计算一次。在去重这个问题上,像Neo4j、TigerGraph、腾讯星图等系统都会出现计算错误的问题。
什么是图算法
关于什么是图算法的问题,至少在2020年业界依然存在很多不同的声音。有一些场景把广度优先搜索(BFS)、深度优先搜索(DFS)作为图算法。这个提法很有趣,不过BFS和DFS应该被看做图上的最基础的2种遍历模式,绝大多数图上的搜索、查询、计算或更复杂的操作的基础都是依赖这两者的(是的,有些操作是可能混搭BFS与DFS的!)。
图算法指的是因需要对图上的部分或全部的数据进行批量处理而所需实现的计算逻辑,例如度算法、中心度算法、排序算法、传播类算法、相似度算法、聚类算法、社区识算法、图嵌入算法、随机游走算法等等。图算法的计算量通常会和图的数据量以及拓扑结构相关,通常意义上,越大的图,计算复杂度度越高,拓扑结构约复杂的图,图计算的复杂度越大。传统意义上的图算法的时耗通常在T+1甚至更久。但是,在成本可控的条件下,可以实现 T+0或准实时、实时计算显然是具有重大意义的。
典型的大计算量的图算法有很多,例如:
·全图K邻查询,例如计算全图所有顶点的3度邻居(3-Hop),并把结果写回图数据库,这个操作相当于动态的为每个顶点增加1个“#3-hop”的属性。同样的,你也可以计算任意深度的K-hop,K值越大,计算复杂度越高。
· Struc2Vec作为2017最新引入的图嵌入算法,它的计算量也非常之大,甚至比全图K-Hop还要指数级的更为复杂。
· Louvain鲁汶社区识别,鲁汶的特点是需要对全图所有的点边进行多次迭代运算,收敛后把顶点聚类,形成不同的社区。鲁汶的计算复杂度(及时间复杂度)较PageRank而言会复杂很多倍,并且需要很高的代码执行并发改造技巧才可能让鲁汶快速运行。
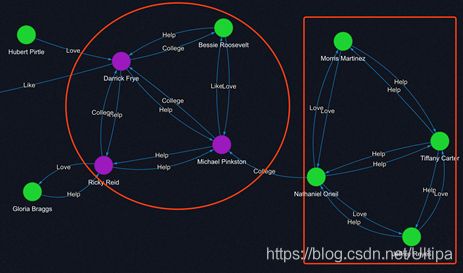
还有一些图算法的复杂度与图的拓扑结构高度相关,例如三角形计数(Triangle Counting),在有些场景下,例如银行转账数据,如果三个账户间存在两两账户间的多笔转账,那么就会形成大量的三角形,例如2亿的账户间仅仅6亿笔交易,但是可能会形成万亿量级的三角形。例如上图中的红圈内的三个紫色顶点间实际上形成了8个三角形(222),尽管只有6条边。这个时候,任意两个紫色顶点间只要增加1条边,就会新生成至少4个三角形,如果这条新的边是在Darrick Frye和Michael Pinkston之间生成,则会产生至少8个新的三角形!这也是为什么图算法的计算复杂度可能会随着图的拓扑结构的变化而高度增加。
在三角形计数中,很多图计算系统的计数方法是存在问题的。一个具备唯一性的三角形它的定义的标准是:三个顶点与三条相连的边所构成的空间拓扑结构(图形)。因为每条边实际上都是由两个顶点相连而成的,因此三角形计数可以只统计三条首尾相连的边即可。但是,像Neo4j系统,它的三角形计数只按照顶点的集合来统计。这两种计数方法会有很大的结果差异性!如下图所示:在一个40万顶点,400万条边的图中,按照顶点统计的三角形有5.1万个,但是按照边来统计有接近100万个!
为了向后兼容和便于理解,Ultipa系统提供了两种计数方法:
什么是图查询语言?
严格意义上说,所有的数据库都需要有自己的查询语言,我们最为熟知的当然是SQL。从关系型数据库开始SQL得到了广泛的应用,它是面向数据库的查询、操作与开发的核心接口。同样的,图数据库也有自己的QL。在数据库家族,过去40年实际上只有2个国际标准,一个是已经非常成熟的SQL,第二个是GQL(Graph Query Language),但是这一标准还没有最终定稿(预计会在~2022年定稿)。在此之前,不同的图数据库的依然在采用不同风格的图查询语言来实现与数据库的对接。
为什么图数据库需要自己的查询语言而不是复用SQL呢?这个问题的答案的本质在于图数据库是高维的数据结构,而SQL所应对的是二维的关系表及其数据结构。用低维的SQL几乎没办法来解决高维的图数据库中的挑战。例如K-Hop、路径查询这些图上面的操作天然的是递归式的,像广度优先搜索或深度优先搜索,这些都是SQL非常难以描述与实现的 – 或者说实现的效率非常低下。
举个金融行业中会经常遇到的问题,查一下某家公司的投资方股东网络,找到该公司的所有股东(或最终受益人、实际控制人等……)。下面这张截图中左侧的几十行SQL代码是来计算股东列表的,而右下角的半行代码是使用Ultipa Query Language (uQL)来实现的。前者在1000个实体1000条关系的投资网络(Mysql表实现)中需要38秒来完成查询(并且无法规避环路),而后者在同样的硬件环境下,只需要1ms!图数据库对于关系型数据库存在数万倍的性能优势。而且随着查询的深度的增加,这种性能优势会指数级上升。

下面我们再举几个典型的图上的查询的例子:
1.从某顶点出发,以BFS的方式展开,限定最大展开4000条边
2.给定的多个顶点,自动组网(限定深度为4,两两节点间最多5条边)
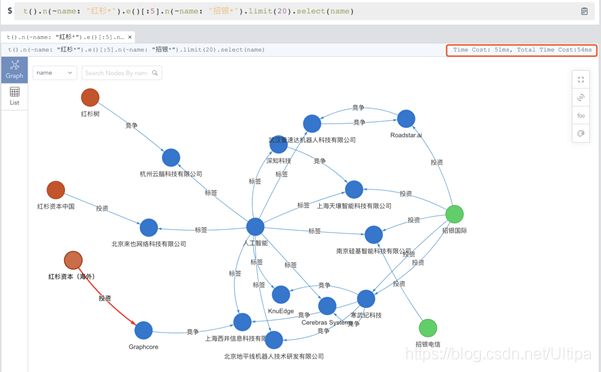
3.模糊的搜索从“红杉***”出发到“招银***”的关联关系网络,网络中的路径搜索深度不超过5层,返回20条路径所构成的子图。
一门先进的(数据库)查询语言的优美感,不是通过它到底有多复杂,而是通过它有多简洁来体现的。它应该具备这样的一些通性:
•易学、易懂(Easy to Learn,Easy to Understand)
•高性能(Lightning Fast):当然,其实这个其实取决于底层的数据库引擎!
•系统的底层复杂性不应该暴露到语言接口层面(System Complexity Shielded-Off)
图数据库查询语言还在不断的迭代进化中,但是希望上面的例子可以让大家感受到UQL(或者说是GQL应该有的样子)的强大威力以及它的便捷性。
并不是所有的图数据库的查询语言都是相同的,Cypher, Gremlin, SPARQL等等,不一而足。uQL没有采用Cypher等的设计理念,最主要的区别如下:
•Cypher, Gremlin, SPARQL……
–无法表达高维数据以及其组合,如,路径,点,边,属性,聚合运算结果集。
–路径过滤过于复杂且性能低效,如路径搜索,模板搜索,图遍历。
–阅读起来与人脑呈相反逻辑,如嵌套语句,连表搜索等。
•uQL or GQL’s future……
–可以返回并使用多维结果(支持子图路径,点边,属性,Table 等高级数据结构) 。
–可以轻松描绘子图过滤,且保证性能零损耗。
–阅读与书写方式与人脑一致。
–链式调用&函数式风格,天然支持功能扩展,“链”本身就是一条路径。
例如下面的例子,同样的查询效果,用Cypher vs. uQL:

![]()
UQL的链式函数调用风格、书写与人脑工作方式一致、实时子图深度过滤等能力是类SQL语言所无法比拟的。