迪杰斯特拉算法实现-Go语言
迪杰斯特拉算法实现-Go语言
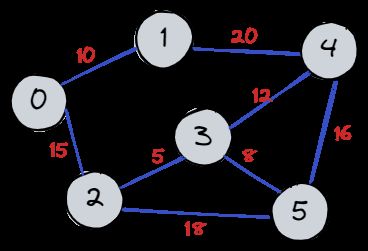
带权值邻接矩阵
邻接矩阵为二维数组:graph[i][j]代表 i 到 j 边的权值,若无方向则对角线对称。
对应的带权值的邻接矩阵为
{
{0 ,10 ,15 ,INF,INF,INF},
{10 ,0 ,INF,INF,20 ,INF},
{15 ,INF,0 ,5 ,INF,18 },
{INF,INF,5 ,0 ,12 ,8 },
{INF,20 ,INF,12 ,0 ,16 },
{INF,INF,18 ,8 ,16 ,0 },
}
算法思路
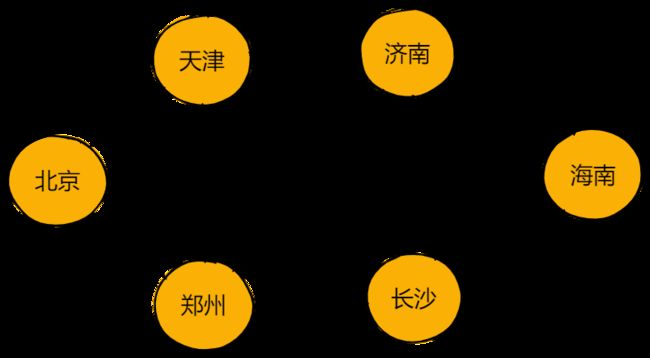
寻找从北京初始位置到海南结点的最短路径
- 用
visit数组记录该节点是否已经访问过 - 用
dist数组来记录起始点到其他结点的最短路径 - 先初始化访问起点更新最短路径
- 遍历未访问过的结点
- 先找出未访问且路径最短的结点
- 从该结点更新其他路径的权值
- 标记访问完成
代码实现
package main
import "fmt"
const INF = 0x3f3f3f3f
// 迪杰斯特拉函数
func dijkstra(graph [][]int, start int) []int {
n := len(graph) // 图中顶点个数
visit := make([]int, n) // 标记已经作为中间结点完成访问的顶点
dist := make([]int, n) // 存储从前点到其他顶点的最短路径
for i := 0; i < n; i++ {
dist[i] = graph[start][i] // 初始化遍历起点
}
visit[start] = 1 // 标记初始顶点
var minDist, midNode int
// 更新其他顶点最短路径,循环n次
for i := 0; i < n; i++ {
minDist = INF // 存储从起点到其他未被访问的结点中的最短路径
midNode = 0 // 存储最短路径的结点编号
// 遍历n个顶点,寻找未被访问且距离为起始位置到该点距离最小的顶点
for j := 0; j < n; j++ {
if visit[j] == 0 && minDist > dist[j] {
minDist = dist[j] // 更新未被访问结点的最短路径
midNode = j // 更新顶点编号
}
}
// 以midNode为中间结点,再循环遍历其他节点更新最短路径
for j := 0; j < n; j++ {
// 若该节点未被访问且找到更短路径即更新最短路径
if visit[j] == 0 && dist[j] > dist[midNode]+graph[midNode][j] {
dist[j] = dist[midNode] + graph[midNode][j]
}
}
visit[midNode] = 1 // 标记已访问
}
return dist
}
func main() {
// 带权值邻接矩阵
var gp = [][]int{
{0, 100, 1200, INF, INF, INF},
{100, 0, 900, 300, INF, INF},
{1200, 900, 0, 400, 500, INF},
{INF, 300, 400, 0, 1300, 1400},
{INF, INF, 500, 1300, 0, 1500},
{INF, INF, INF, 1400, 1500, 0},
}
dist := dijkstra(gp, 0)
fmt.Println(dist[5]) // 1800
}