通过模拟退火改进的Elman神经网络（Matlab代码实现）

       目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

神经网络是一个庞大的体系和概念，根据处理信息的不同方式来区分不同的network。比如根据处理信息结果的传递方向，分前馈型与反馈型。前馈型网络会根据输出数值来调整网络的参数，反馈型网络的输入会存在输入或者输出数值的反馈，可以对运算处理过程不断地进行优化。网络的反馈形式决定了网络的动态运算特点，递归神经网络ELMAN和前面所介绍的三层BP神经网络相比，增加了一个承接层，可以理解成延时算子，作用是让网络存在记忆功能，更好地适应数据输入的动态变化。

ELMAN的构造分为四层神经元：输入层、隐含层、承接层以及输出层（在使用智能算法优化ELMAN的参数时，理解ELMAN的结构将有所帮助）。

a). 输入层、输出层的神经元节点个数：

输入层的神经元数量与输入数据特征的维数是相等的，输出层的神经元节点数量也等同于输出数据标签的维度，这与BP神经网络一样。

b). 隐含层的神经元节点个数：

不管在BP还是ELMAN,或者其他的神经网络，隐含层的神经元个数都不是固定的。如果选择的隐含层神经元个数较少时，就会导致网络的学习程度减小甚至无法学习。节点个数较多时，则会导致网络训练的过程变慢，也很难得出预计的情况。只有当隐含层神经元数量只有控制在一个合理的范围内，才能使得网络模型好的进行学习运算。

c). 承接层的神经元节点个数：
承接层也叫做上下文层和状态层，主要功能是用来记忆隐含层上一个时间点的输出数值。所以承接层的神经元个数与隐含层相同，确定方法为：先根据训练误差最小确定最佳的隐含层神经元节点，再得到承接层的神经元节点个数。​

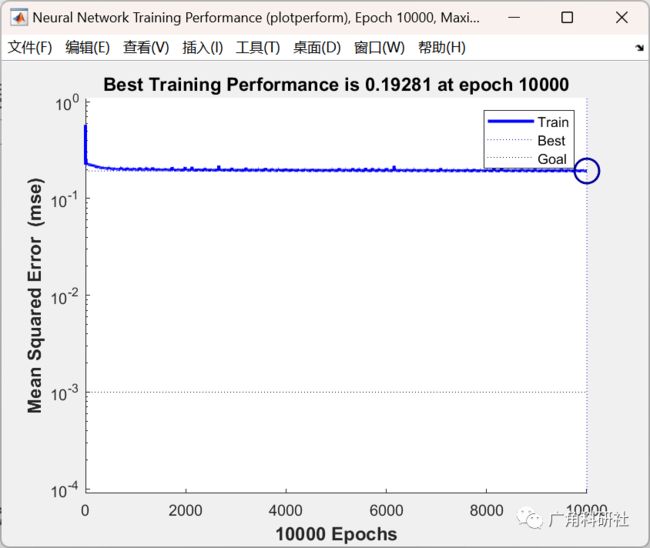
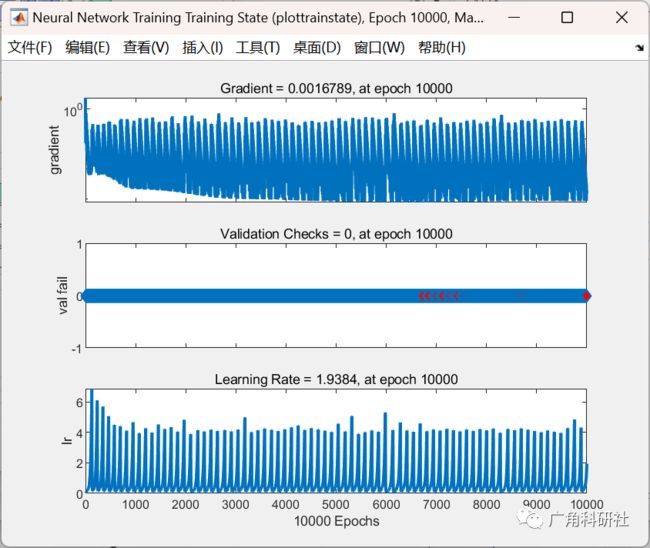
2 运行结果

主函数部分代码：

clc; 

clear all; 

close all; 

warning off; 

p_Input_Vector= [0.358575915 0.498850877 1.376188585 18.3089 0.3582 -0.568942758 0.4485 1.4605...

-0.4642 0.311355024 18.4289 0.580949408 -1.615989276 1.3321 0.2879  -0.1842...

0.1253 1.0623 1.9955 0.9253 -0.8522 1.6985 1.6186 0.5374 -0.4550...

1.3720 0.2887 -0.2054 1.1227 0.0407 1.8810 1.8039 1.7292 0.6573...

0.5885 -0.5233 1.4620 -1.4050 -0.3527 0.2637 0.2278 0.1981 1.1750...

1.1589 1.1502 0.1493 1.1565 -0.1722  0.2308 0.2745 1.3282 1.3923...

0.5535 -1.6514 0.7612  1.0183 0.1664 -0.3280  1.6934...

0.8979; 0.0884 0.1100  0.1100 1.1074 -0.1047  0.1047 0.1154 -0.1100...

-0.0938  0.0993 0.1154 0.1233 1.1180 1.1207 0.1233  0.1233...

-0.1312 0.1233 0.1233 1.1207 1.1154  1.1312 1.1286 0.1312 1.1154...

0.1100 0.1127 -0.1180 0.1154 -0.1154 0.1180 0.1312 1.1417 1.1207...

1.1233 2.1286 2.1233 2.1233 1.1207  -0.1180 -0.1286 -0.1468 0.1286...

-0.1417 -1.1391 -1.1391 -0.1233 0.1339 0.1365 0.1442 0.1417 0.1312...

0.1365 1.1365 1.1154  1.1180 1.1127 0.1312  0.1233...

0.1100];

t_Target_Vector=[-0.223179685 -0.42730107  0.589010207  0.339141758  -0.451268411  0.194179725  -1.65506949  0.356492333...

-2.468671371 -0.250678404  -0.7470808  -0.992710553  0.96476692  1.6939  0.6878  0.96476692   -2.468671371  0.194179725  0.356492333  0.6512  -0.793039853  0.6329  0.6268  -0.992710553  -2.468671371... 

0.356492333  0.6024  1.5960363  -0.442548724  0.5841  1.5719  0.5658  0.194179725  -0.992710553... 

0.96476692  -0.793039853  -1.1236752  0.5292  0.194179725  0.5109  0.5048  -0.962528123  -0.442548724...

-0.4456865  -1.65506949  -0.962528123  0.356492333  -2.468671371  -0.250678404  -0.793039853  0.194179725  -0.992710553 0.2700  0.356492333  -1.65506949    -0.962528123  0.96476692  0.0900   -0.442548724... 

0];

P_test=[10.9 13.4 15.5 16.7 17.1 17.5 18.1 19.2 22.3 26.4 ;9.4 8.2 7.5 6.4 7.3 7.75 6.8 9.5 11.4 13.9] ;

t1=[0.9568    0.8954    0.8323    0.7099    0.7041    0.6748    0.5276    0.5769    0.5624    0.4148];

[pn,minp,maxp,tn,mint,maxt]=premnmx(p_Input_Vector,t_Target_Vector);

p2= tramnmx(P_test,minp,maxp);

net=newelm(minmax(pn),[5,1],{'tansig','purelin'});

net.trainparam.epochs=10000;

net.trainparam.show=100;

net.trainparam.goal=0.001;

net.trainParam.lr=0.1;

net=init(net);

[net,tr]=train(net,pn,tn);

PN=sim(net,p2);

t2= postmnmx(PN,mint,maxt);

plot(1:1:10,t1,'-ko','linewidth',2);

hold on;

plot(1:1:10,t2,'--k+','linewidth',2);

3 参考文献

​[1]韩旭明. Elman神经网络的应用研究[D].天津大学,2006.