【数据结构与算法】散列查找
本文由 程序喵正在路上 原创,CSDN首发!
系列专栏:数据结构与算法
首发时间:2022年12月8日
欢迎关注点赞收藏留言
一以贯之的努力 不得懈怠的人生
阅读指南
- 散列表
- 常见的散列函数
- 开放定址法
- 再散列法
散列表
散列表( H a s h T a b l e Hash \ Table Hash Table),又称哈希表,是一种数据结构,特点是:数据元素的关键字与其存储地址直接相关
那么我们如何建立 “关键字” 与 “存储地址” 之间的联系呢?
—— 通过 “散列函数”(哈希函数): A d d r = H ( k e y ) Addr = H(key) Addr=H(key)
若不同的关键字通过散列函数映射到同一个值,则称它们为 “同义词”;通过散列函数确定的位置已经存放了其他元素,则称这种情况为 “冲突”
那我们怎么解决 “冲突” 呢?
—— 用拉链法(又称链接法、链地址法)处理 “冲突”:把所有 “同义词” 存储在一个链表中,不把空位置的比较算入
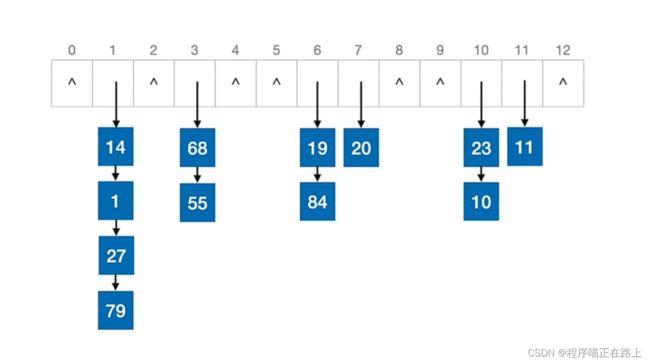
例子:有一堆元素,关键字分别为 { 19 , 14 , 23 , 1 , 68 , 20 , 84 , 27 , 55 , 11 , 10 , 79 } \{19, 14, 23,1, 68, 20, 84, 27, 55, 11, 10, 79\} {19,14,23,1,68,20,84,27,55,11,10,79},散列函数为 H ( k e y ) = k e y % 13 H(key) = key \ \% \ 13 H(key)=key % 13
查找长度 —— 在查找运算中,需要对比关键字的次数称为查找长度
所以上图中查找成功的平均查找长度为 A S L = 1 × 6 + 2 × 4 + 3 + 4 12 = 1.75 ASL = \frac{1 \times 6 + 2 \times 4 + 3 + 4}{12} = 1.75 ASL=121×6+2×4+3+4=1.75
当我们的散列函数设计得足够好时,我们就可以得到最理想的情况,也就是当所有关键字都没有同义词的时候,散列查找时间复杂度可达到 O ( 1 ) O(1) O(1)
上图查找失败的平均查找长度为 A S L = 0 + 4 + 0 + 2 + 0 + 0 + 2 + 1 + 0 + 0 + 2 + 1 + 0 13 = 0.92 ASL = \frac{0 + 4 + 0 + 2 + 0 + 0 + 2 + 1 + 0 + 0 + 2 + 1 + 0}{13} = 0.92 ASL=130+4+0+2+0+0+2+1+0+0+2+1+0=0.92
下面我们认识一个新的概念:装填因子 α = \alpha = α= 表中记录数 / / / 散列表长度,也就是前面的 0.92 0.92 0.92 ;装填因子会直接影响散列表的查找效率
常见的散列函数
① 除留余数法 —— H ( k e y ) = k e y % p H(key) = key \ \% \ p H(key)=key % p
散列表表长为 m m m,取一个不大于 m m m 但最接近或等于 m m m 的质数 p p p
② 直接定址法 —— H ( k e y ) = k e y H(key) = key H(key)=key 或 H ( k e y ) = a × k e y + b H(key) = a \times key + b H(key)=a×key+b
其中, a a a 和 b b b 是常数。这种方法计算最简单,且不会产生冲突。它适合关键字的分布基本连续的情况,若关键字分布不连续,空位极多,则会造成存储空间的浪费
③ 数字分析法 —— 选取数码分布较为均匀的若干位作为散列地址
设关键字是 r r r 进制数(如十进制数),而 r r r 个数码在各位上出现的频率不一定相同,可能在某些位置上分布均匀一些,各种数码出现的机会均等;而在某些位上分布不均匀,只有某几种数码经常出现,此时可选取数据分布较为均匀的若干位作为散列地址。这种方法适用于已知的关键字集合,若更换了关键字,则需要重新构造新的散列函数
④ 平方取中法 —— 取关键字的平方值的中间几位作为散列地址
具体取多少位要视实际情况而定。这种方法得到的散列地址与关键字的每位都有关系,因此使得散列地址比较均匀,适用于关键字的每位取值都不够均匀或均小于散列地址所需的位数
散列表是典型的 “用空间换时间” 的算法,只要散列函数设计得合理,则散列表越长,冲突的概率越低
开放定址法
所谓开放定址法,是指可存放新表项的空闲地址既向它的同义词表项开放,又向它的非同义词表项开放。其数学递推公式为:
H i = ( H ( k e y ) + d i ) % m H_i = (H(key) + d_i) \ \% \ m Hi=(H(key)+di) % m
i = 0 , 1 , 2 , . . . , k ( k ≤ m − 1 ) i = 0, 1, 2, ..., k \ (k \leq m- 1) i=0,1,2,...,k (k≤m−1), m m m 表示散列表表长, d i d_i di 为增量序列, i i i 可理解为 “第 i i i 次发生冲突”
想要确定增量序列 d i d_i di,我们需要学习下面 3 3 3 种方法
① 线性探测法 —— d i = 0 , 1 , 2 , 3 , . . . , m − 1 d_i = 0, 1, 2, 3, ..., m - 1 di=0,1,2,3,...,m−1;即发生冲突时,每次往后探测相邻的下一个单元是否为空
例子:有一堆元素,关键字分别为 { 19 , 14 , 23 , 1 , 68 , 20 , 84 , 27 , 55 , 11 , 10 , 79 } \{19, 14, 23,1, 68, 20, 84, 27, 55, 11, 10, 79\} {19,14,23,1,68,20,84,27,55,11,10,79},散列函数为 H ( k e y ) = k e y % 13 H(key) = key \ \% \ 13 H(key)=key % 13,假设散列表表长为 16 16 16
上面的例子用线性探测法来处理,如下图所示:
这个例子需要注意:
- 散列函数的值域为 [ 0 , 12 ] [0, 12] [0,12]
- 冲突处理函数值域为 [ 0 , 15 ] [0, 15] [0,15]
- 查找时,按照线性探测法进行定位,找不到再一个个往后找,要把空位置的判断也算作一次比较
采用 “开放定址法” 时,删除结点不能简单地将被删结点的空间置为空,否则将截断在它之后填入散列表的同义词结点的查找路径,可以做一个 “删除标记”,进行逻辑删除
查找成功的平均查找长度为 A S L = 1 + 1 + 1 + 2 + 4 + 1 + 1 + 3 + 3 + 1 + 3 + 9 12 = 2.5 ASL = \frac{1 + 1 + 1 + 2 + 4 + 1 + 1 + 3 + 3 + 1 + 3 + 9}{12} = 2.5 ASL=121+1+1+2+4+1+1+3+3+1+3+9=2.5
查找失败的平均查找长度为 A S L = 1 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 13 = 7 ASL = \frac{1 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2}{13} = 7 ASL=131+13+12+11+10+9+8+7+6+5+4+3+2=7
线性探测法很容易造成同义词、非同义词的 “聚集(堆积)” 现象,严重影响查找效率
② 平方探测法 —— 当 d i = 0 2 , 1 2 , − 1 2 , 2 2 , − 2 2 , . . . , k 2 , − k 2 d_i = 0^2, 1^2, -1^2, 2^2, -2^2, ..., k^2, -k^2 di=02,12,−12,22,−22,...,k2,−k2 时,称为平方探测法,又称二次探测法,其中 k ≤ m / 2 k \leq m/2 k≤m/2
例子:有一堆元素,关键字分别为 { 6 , 19 , 32 , 45 , 58 , 71 , 84 } \{6, 19, 32, 45, 58, 71, 84\} {6,19,32,45,58,71,84},散列函数为 H ( k e y ) = k e y % 13 H(key) = key \ \% \ 13 H(key)=key % 13,假设散列表表长为 27 27 27,采用平方探测法处理冲突
需要注意,如果你采用平方探测法来处理冲突,那么散列表的长度 m m m 必须是一个可以表示成 4 j + 3 4j + 3 4j+3 的素数,才能探测到所有位置
③ 伪随机序列法 —— d i d_i di 是一个伪随机序列,如 d i = 0 , 5 , 24 , 11 , . . . d_i = 0, 5, 24, 11, ... di=0,5,24,11,...
再散列法
再散列法(再哈希法):除了原始的散列函数 H ( k e y ) H(key) H(key) 之外,多准备几个散列函数,当散列函数冲突时,用下一个散列函数计算一个新地址,直到不冲突为止:
H i = R H i ( K e y ) i = 1 , 2 , 3 , . . . , k H_i = RH_i(Key) \ \ \ i = 1, 2, 3, ..., k Hi=RHi(Key) i=1,2,3,...,k