基于词法分析的中缀表达式计算
基于词法分析的中缀表达式计算
前面我们对中缀表达式的词法处理进行了讲解并给出了程序示例《四则运算的词法分析》,之前我们也对中缀表达式的计算进行了一系列的分析,诸如《检测中缀表达式的合法性》。在之前的中缀表达式的计算中,我们是利用了空白符来间隔操作符和操作数,这属于一种硬分割。
本文我们利用上一篇中对中缀表达式进行词法分析,进而通过中缀表达式转换为后缀表达式,进而计算后缀表达式来实现基于词法分析的中缀表达式计算。
程序的处理过程主要是包括3个部分:
1.对中缀表达式进行词法分析
2.中缀表达式转化为后缀表达式
3.后缀表达式的计算
我们的程序也是按照以上三个步骤进行的,具体的程序如下:
// 基于词法分析的中缀表达式计算 #include <iostream> #include <sstream> #include <vector> #include <string> #include <stack> #include <map> #include <cassert> using namespace std; string& replace_all_distinct(string& str, const string& src, const string& des) { for (string::size_type i = 0; i != string::npos; i += des.size()) { i = str.find(src, i); if (i != string::npos) { str.replace(i, src.size(), des); } else { break; } } return str; } string& n_replace(string& str, const vector<string>& src, const vector<string>& des) { assert(src.size() > 0 && src.size() == des.size()); for (vector<string>::size_type i = 0; i != src.size(); ++i) { replace_all_distinct(str, src[i], des[i]); } return str; } void get_infix(vector<string>& inf, const vector<string>& src, const vector<string>& des) { inf.clear(); string line; getline(cin, line); n_replace(line, src, des); istringstream sin(line); string tmp; while (sin >> tmp) { inf.push_back(tmp); } } // 加入词法分析 BEGIN struct TI { string token; int id; }; bool is_blank(char ch) { return ch == ' ' || ch == ' '; } void get_exp(string& exp) { getline(cin, exp); } void init_keys(map<string, int>& keys) { keys.clear(); keys["+"] = 1; keys["-"] = 2; keys["*"] = 3; keys["/"] = 4; keys["("] = 5; keys[")"] = 6; keys["__NUM__"] = 7; } void lex(const string& exp, vector<TI>& to_id, const map<string, int>& keys) { to_id.clear(); char ch; for (string::size_type pos = 0; pos < exp.size(); /* ++pos */) { TI ti; ch = exp[pos]; if (is_blank(ch)) { ++pos; continue; } if (ch >= '0' && ch <= '9' || ch == '.') { ti.token += ch; ++pos; if (pos >= exp.size()) { ti.id = keys.size(); to_id.push_back(ti); return; } ch = exp[pos]; while (ch >= '0' && ch <= '9' || ch == '.') { ti.token += ch; ++pos; if (pos >= exp.size()) { ti.id = keys.size(); to_id.push_back(ti); return; } ch = exp[pos]; } ti.id = keys.size(); to_id.push_back(ti); } else { map<string, int>::const_iterator cit; switch (ch) { case '+': case '-': case '*': case '/': case '(': case ')': ti.token += ch; cit = keys.find(ti.token); if (cit == keys.end()) { cout << "test" << endl; } ti.id = cit->second; to_id.push_back(ti); ++pos; break; default: // ti.token += string("Unknown:") + ch; ti.token += string("未知字符:") + ch; ti.id = -1; to_id.push_back(ti); ++pos; break; } } } } // 基于词法分析读取中缀表达式 void get_infix_lex(vector<string>&inf, const map<string, int>& keys) { inf.clear(); string line; getline(cin, line); vector<TI> to_id; lex(line, to_id, keys); for (vector<TI>::size_type i = 0; i != to_id.size(); ++i) { inf.push_back(to_id[i].token); } } // 加入词法分析 END void show(const vector<string>& hs) { for (vector<string>::size_type i = 0; i != hs.size(); ++i) { cout << hs[i] << ' '; } cout << endl; } void init_op(map<string, int>& ops) { ops.clear(); ops["+"] = 100; ops["-"] = 100; ops["*"] = 200; ops["/"] = 200; ops["("] = 1000; ops[")"] = 0; } bool is_operator(const string& hs, const map<string, int>& ops) { map<string, int>::const_iterator cit = ops.find(hs); if (cit != ops.end()) { return true; } else { return false; } } // 判断操作数是否合法 bool op_legal(const string& str, int& ill_id) { assert(str.size() > 0); string::size_type i = 0; if (str[i] == '+' || str[i] == '-') { ++i; if (i == str.size()) { ill_id = 3001; return false; } } int dot_num = 0; for (; i != str.size(); ++i) { // if (isdigit(static_cast<int>(str[i]))) if (str[i] >= '0' && str[i] <= '9') { ; } else if (str[i] == '.') { ++dot_num; } else { ill_id = 3002; return false; } } if (dot_num > 1) { ill_id = 3003; return false; } return true; } void in2post(const vector<string>& inf, vector<string>& postf, map<string, int>& ops, bool& leg, int& ill_id) { if (inf.size() == 0) { leg = false; ill_id = 6001; return; } postf.clear(); stack<string> op_st; // 记录左括号和右括号之间的数量关系 int brac = 0; int op_op = 0; for (vector<string>::size_type i = 0; i != inf.size(); ++i) { if (!is_operator(inf[i], ops)) { // 判断是否是正确的操作数 int tmp = 0; if (!op_legal(inf[i], tmp)) { leg = false; ill_id = tmp; return; } ++op_op; if (op_op > 1) { leg = false; ill_id = 5001; return; } postf.push_back(inf[i]); } else { if (inf[i] == "(") { ++brac; op_st.push(inf[i]); } else if (inf[i] == ")") { --brac; if (brac < 0) { leg = false; ill_id = 4001; return; } while (!op_st.empty()) { if (op_st.top() == "(") { op_st.pop(); break; } else { postf.push_back(op_st.top()); op_st.pop(); } } } else // 若为其他运算符 { --op_op; if (op_op < 0) { leg = false; ill_id = 5002; return; } if (op_st.empty()) // 若为空栈,则直接入栈 { op_st.push(inf[i]); } else { if (ops[inf[i]] > ops[op_st.top()]) { // 如果当前操作符优先级高于站定操作符优先级 // 则直接入栈 op_st.push(inf[i]); } else { // 否则弹出栈中优先级大于等于当前操作符优先级 // 的操作符,并最后将当前操作符压栈 while (!op_st.empty() && ops[op_st.top()] >= ops[inf[i]] && op_st.top() != "(") { postf.push_back(op_st.top()); op_st.pop(); } op_st.push(inf[i]); } } } } } if (brac > 0) { leg = false; ill_id = 4002; return; } if (op_op != 1) { leg = false; ill_id = 5003; return; } while (!op_st.empty()) { postf.push_back(op_st.top()); op_st.pop(); } leg = true; return; } double cal_post(const vector<string>& postf, const map<string, int>& ops, bool& leg, int& ill_id) { stack<double> or_st; double operand = 0.0, a = 0.0, b = 0.0, c = 0.0; for (vector<string>::size_type i = 0; i != postf.size(); ++i) { if (!is_operator(postf[i], ops)) { operand = static_cast<double>(atof(postf[i].c_str())); or_st.push(operand); } else { switch (postf[i][0]) { case '+': // 检测后缀表达式的合法性:操作数是否足够 if (or_st.size() < 2) { leg = false; ill_id = 1001; return -10000000000000.0; } b = or_st.top(); or_st.pop(); a = or_st.top(); or_st.pop(); c = a + b; or_st.push(c); break; case '-': // 检测后缀表达式的合法性:操作数是否足够 if (or_st.size() < 2) { leg = false; ill_id = 1002; return -10000000000000.0; } b = or_st.top(); or_st.pop(); a = or_st.top(); or_st.pop(); c = a - b; or_st.push(c); break; case '*': // 检测后缀表达式的合法性:操作数是否足够 if (or_st.size() < 2) { leg = false; ill_id = 1003; return -10000000000000.0; } b = or_st.top(); or_st.pop(); a = or_st.top(); or_st.pop(); c = a * b; or_st.push(c); break; case '/': // 检测后缀表达式的合法性:操作数是否足够 if (or_st.size() < 2) { leg = false; ill_id = 1004; return -10000000000000.0; } b = or_st.top(); or_st.pop(); a = or_st.top(); or_st.pop(); c = a / b; or_st.push(c); break; default: break; } } } if (or_st.size() == 1) { leg = true; return or_st.top(); } else // 检测后缀表达式的合法性:操作数是否有多余 { leg = false; ill_id = 2001; return -10000000000000.0; } } void init_src_des(vector<string>& src, vector<string>& des) { src.push_back("+"); src.push_back("-"); src.push_back("*"); src.push_back("/"); src.push_back("("); src.push_back(")"); des.push_back(" + "); des.push_back(" - "); des.push_back(" * "); des.push_back(" / "); des.push_back(" ( "); des.push_back(" ) "); } // 将中缀表达式转换后缀表达式和计算后缀表达式封装合并 double cal_inf(const vector<string>& inf, map<string, int>& ops, bool& leg_trans, bool& leg_cal, int& ill_id) { leg_trans = true; ill_id = 0; vector<string> postf; in2post(inf, postf, ops, leg_trans, ill_id); if (leg_trans) { show(postf); } else { cout << "Trans illegal: " << ill_id << '!' << endl << endl; return -10000000000000.0; } leg_cal = true; ill_id = 0; double ret = cal_post(postf, ops, leg_cal, ill_id); if (leg_cal) { return ret; } else { cout << "Cal illegal: " << ill_id << '!' << endl << endl; return -10000000000000.0; } } int main() { map<string, int> ops; init_op(ops); vector<string> inf; vector<string> src, des; init_src_des(src, des); map<string, int> keys; init_keys(keys); while (1) { // 原来读取后缀表达式的方法(加空格处理) // get_infix(inf, src, des); get_infix_lex(inf, keys); bool leg_trans = true; bool leg_cal = true; int ill_id = 0; double ret = cal_inf(inf, ops, leg_trans, leg_cal, ill_id); if (leg_trans && leg_cal) { cout << ret << endl << endl; } } return 0; }
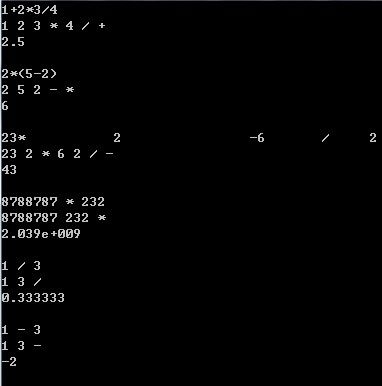
目前我们关于四则运算表达式的计算到此结束。主要分为3大块:
1.对输入的中缀表达式进行词法分析
2.将中缀表达式转换为后缀表达式
3.计算后缀表达式
四则运算的相关处理已基本介绍完毕。接下来会涉及一些前缀表达式、中缀表达式、后缀表达式之间的一些相互转换。
关于中缀表达式的计算我们是利用了两个栈——操作符栈和操作数栈进行的。对于中缀表达式另外的计算方法有待我们以后进一步探讨。