SHA256算法详解及python实现

1.SHA256介绍（可略过）

SHA256是SHA-2下细分出的一种算法。SHA-2（安全哈希算法2）是由美国国家安全局（NSA）设计的一组加密哈希函数。SHA-2系列由六个具有224、256、384或512位摘要（哈希值）的哈希函数组成：SHA-224，SHA-256，SHA-384，SHA-512，SHA-512 / 224，SHA -512/256。SHA-256和SHA-512是分别用32位和64位字计算的哈希函数。它们使用不同的移位量和加性常数，但是它们的结构实际上是相同的，只是轮数不同。

SHA256其实就是一个哈希函数。哈希函数，又称散列算法，是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要，使得数据量变小，将数据的格式固定下来。该函数将数据打乱混合，重新创建一个叫做散列值（或哈希值）的指纹。散列值通常用一个短的随机字母和数字组成的字符串来代表。

对于任意长度的消息，SHA256都会产生一个256bit长的哈希值，称作消息摘要。这个摘要相当于是个长度为32个字节的数组，通常用一个长度为64的十六进制字符串来表示。

2. SHA算法详解

2.1常量初始化
SHA256算法中用到了8个哈希初值以及64个哈希常量。
SHA256算法的8个哈希初值为前8个质数（2,3,5,7,11,13,17,19）的平方根的小数部分取前32bit而来，如下所示（8个哈希值为图中的1所框出的部分，即第一次迭代的（A,B,…,H）值）：

h0 := 0x6a09e667
h1 := 0xbb67ae85
h2 := 0x3c6ef372
h3 := 0xa54ff53a
h4 := 0x510e527f
h5 := 0x9b05688c
h6 := 0x1f83d9ab
h7 := 0x5be0cd19

#对于$\sqrt{2}$≈0.414213562373095048，而0.414213562373095048≈$6\times 16^{-1}+a\times 16^{-2}+0\times 16^{-3}+9\times 16^{-4}+e\times 16^{-5}+6\times 16^{-6}+6\times 16^{-7}+7\times 16^{-8}$。故质数2的平方根的小数部分取前32bit就对应出了0x6a09e667。

在SHA256算法中，用到的64个常量如下：

428a2f98 71374491 b5c0fbcf e9b5dba5
3956c25b 59f111f1 923f82a4 ab1c5ed5
d807aa98 12835b01 243185be 550c7dc3
72be5d74 80deb1fe 9bdc06a7 c19bf174
e49b69c1 efbe4786 0fc19dc6 240ca1cc
2de92c6f 4a7484aa 5cb0a9dc 76f988da
983e5152 a831c66d b00327c8 bf597fc7
c6e00bf3 d5a79147 06ca6351 14292967
27b70a85 2e1b2138 4d2c6dfc 53380d13
650a7354 766a0abb 81c2c92e 92722c85
a2bfe8a1 a81a664b c24b8b70 c76c51a3
d192e819 d6990624 f40e3585 106aa070
19a4c116 1e376c08 2748774c 34b0bcb5
391c0cb3 4ed8aa4a 5b9cca4f 682e6ff3
748f82ee 78a5636f 84c87814 8cc70208
90befffa a4506ceb bef9a3f7 c67178f2

这些常量是对自然数中前64个质数(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,
53,59,61,67,71,73,79,83,89,97…)的立方根的小数部分取前32bit而来（图中64次迭代的Kt值）。
2.2预处理

SHA256对进入的信息要进行初始化，即使消息满足指定结构。信息处理主要是消息填充和附加长度。（1.通过在消息后增加0，使消息达到指定长度。2.并在最后增加消息长度信息）

（1）在报文末尾进行填充，使报文长度在对512取模以后的余数是448。
填充是这样进行的：先补第一个比特为1，然后都补0，直到长度满足对512取模后余数是448。信息必须进行填充，也就是说，即使长度已经满足对512取模后余数是448，补位也必须要进行，这时要填充512个比特。（即最少补一位，最多补512位）。
（2）这里余数是448的原因是填充后，会再附加上一个64bit的数据，用来表示原始报文的长度信息。而448+64=512，正好拼成了一个完整的结构。附加的64bit的数据，即用一个64位的数据表示原始消息的长度（故消息长度必须小于2^64）。长度信息的编码方式为64-bit big-endian integer（可以简单地理解成，从最高位开始数数字长度）。

2.3逻辑运算

逻辑运算	含义
∧	按位“与”
¬	按位“补”
⊕	按位“异或”
$S^n$	循环右移n个bit
$R^n$	右移n个bit

涉及的逻辑函数：
$$Ch(x,y,z)=(x\wedge y)\oplus (\neg x\wedge z)$$
$$Ma(x,y,z)=(x\wedge y)\oplus (x\wedge z)\oplus (y\wedge z)$$
$$\Sigma 0(x)=S^2(x)\oplus S^{1}3(x)\oplus S^{2}2(x)$$
$$\Sigma 1(x)=S^6(x)\oplus S^{1}1(x)\oplus S^{2}5(x)$$
$$\sigma 0(x)=S^7(x)\oplus S^{1}8(x)\oplus S^3(x)$$
$$\sigma 1(x)=S^{1}7(x)\oplus S^{1}9(x)\oplus S^{1}0(x)$$
$$田(x,y)=(x+y)mod{2}^{32}$$

2.4计算消息摘要
（1）将消息分解成512bit的若干块。此处若是消息被分成n块，则整个代码就要完成n个64迭代（图中的一次运算为1个迭代，每个块要经过64次迭代）。
（2）构造64个字，对于消息分解成的每个512bit的块，需要构成64个字（每个字节是8位二进制，每个字有4个字节，故每个字有32bit）。前16个字直接由原消息组成，记为W[0] 、…W[15]。对于其余字则有迭代公式计算而得：
$$W_t=\sigma 1(W_{t-2})+W_{t-7}+\sigma 0(W_{(}t-15))+W_{t-16}$$
（3）进行64次加密循环。

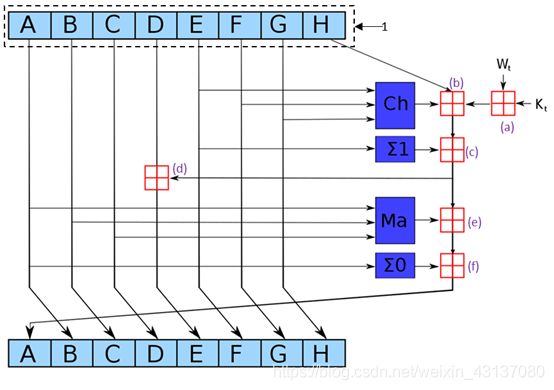
第一次迭代时，A、B、…H是8个哈希初始值（见2.1）。
在（a）处：（a）=$田(W_t,K_t)$。（$W_t$为2.4（2）中构造的字，$K_t$为2.1中的哈希常量）。
在（b）处：(b)= 田(Ch(E,F,G), H, (a))。
在（c）处：（c）= 田(Σ1(E), (b))。
在（d）处：(d)= 田(D,（c）)。
在（e）处：(e)= 田(Ma(A,B,C),（c）)。
在（f）处：(f)= 田(Σ0(A),(e))。

一次循环可计算得：Bi=A，Ci=B，Di=C，Ei=(d)，Fi=E,Gi=F,Hi=G,Ai=(f)。

经过64次迭代，可以得到第一个512块函数的摘要。

对于下一个512bit的块，将压缩块添加到当前哈希值:h0：= h0 + Ai；h1：= h1 + Bi；h2：= h2 + Ci；h3：= h3 + Di；h4：= h4 + Ei；h5：= h5 + Fi；h6：= h6 + Gi；h7：= h7 + Hi。
(h0,…,h7初始值见2.1)

最后的计算的SHA256的值为：digest= h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7。（将h0,…h7连接起来）

3. SHA256伪代码

（同wiki）

Note 1: All variables are 32 bit unsigned integers and addition is calculated modulo 232
Note 2: For each round, there is one round constant k[i] and one entry in the message schedule array w[i], 0 ≤ i ≤ 63
Note 3: The compression function uses 8 working variables, a through h
Note 4: Big-endian convention is used when expressing the constants in this pseudocode,
    and when parsing message block data from bytes to words, for example,
    the first word of the input message "abc" after padding is 0x61626380

Initialize hash values:
(first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19):
h0 := 0x6a09e667
h1 := 0xbb67ae85
h2 := 0x3c6ef372
h3 := 0xa54ff53a
h4 := 0x510e527f
h5 := 0x9b05688c
h6 := 0x1f83d9ab
h7 := 0x5be0cd19

Initialize array of round constants:
(first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311):
k[0..63] :=
   0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
   0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
   0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
   0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
   0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
   0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
   0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
   0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2

Pre-processing (Padding):
begin with the original message of length L bits
append a single '1' bit
append K '0' bits, where K is the minimum number >= 0 such that L + 1 + K + 64 is a multiple of 512
append L as a 64-bit big-endian integer, making the total post-processed length a multiple of 512 bits

Process the message in successive 512-bit chunks:
break message into 512-bit chunks
for each chunk
    create a 64-entry message schedule array w[0..63] of 32-bit words
    (The initial values in w[0..63] don't matter, so many implementations zero them here)
    copy chunk into first 16 words w[0..15] of the message schedule array

    Extend the first 16 words into the remaining 48 words w[16..63] of the message schedule array:
    for i from 16 to 63
        s0 := (w[i-15] rightrotate  7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift  3)
        s1 := (w[i- 2] rightrotate 17) xor (w[i- 2] rightrotate 19) xor (w[i- 2] rightshift 10)
        w[i] := w[i-16] + s0 + w[i-7] + s1

    Initialize working variables to current hash value:
    a := h0
    b := h1
    c := h2
    d := h3
    e := h4
    f := h5
    g := h6
    h := h7

    Compression function main loop:
    for i from 0 to 63
        S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)
        ch := (e and f) xor ((not e) and g)
        temp1 := h + S1 + ch + k[i] + w[i]
        S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)
        maj := (a and b) xor (a and c) xor (b and c)
        temp2 := S0 + maj
 
        h := g
        g := f
        f := e
        e := d + temp1
        d := c
        c := b
        b := a
        a := temp1 + temp2

    Add the compressed chunk to the current hash value:
    h0 := h0 + a
    h1 := h1 + b
    h2 := h2 + c
    h3 := h3 + d
    h4 := h4 + e
    h5 := h5 + f
    h6 := h6 + g
    h7 := h7 + h

Produce the final hash value (big-endian):
digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7

4. python实现代码

github链接

class SHA256:
    def __init__(self):
        #64个常量
        #图中Kt
        self.constants = (
            0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5,
            0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
            0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
            0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
            0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc,
            0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
            0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
            0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
            0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
            0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
            0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3,
            0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
            0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5,
            0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
            0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
            0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2)
        #迭代初始值，h0,h1,...,h7
        self.h = (
            0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a,
            0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19)

    #x循环右移b个bit
    #rightrotate b bit
    def rightrotate(self, x, b):
        return ((x >> b) | (x << (32 - b))) & ((2**32)-1)

    #信息预处理。附加填充和附加长度值
    def Pad(self, W):
        return bytes(W, "ascii") + b"\x80" + (b"\x00" * ((55 if (len(W) % 64) < 56 else 119) - (len(W) % 64))) + (
            (len(W) << 3).to_bytes(8, "big"))

    def Compress(self, Wt, Kt, A, B, C, D, E, F, G, H):
        return ((H + (self.rightrotate(E, 6) ^ self.rightrotate(E, 11) ^ self.rightrotate(E, 25)) + (
                    (E & F) ^ (~E & G)) + Wt + Kt) + (
                            self.rightrotate(A, 2) ^ self.rightrotate(A, 13) ^ self.rightrotate(A, 22)) + (
                            (A & B) ^ (A & C) ^ (B & C))) & ((2**32)-1), A, B, C, (D + (
                    H + (self.rightrotate(E, 6) ^ self.rightrotate(E, 11) ^ self.rightrotate(E, 25)) + (
                        (E & F) ^ (~E & G)) + Wt + Kt)) & ((2**32)-1), E, F, G

    def hash(self, message):
        message = self.Pad(message)
        digest = list(self.h)

        for i in range(0, len(message), 64):
            S = message[i: i + 64]
            W = [int.from_bytes(S[e: e + 4], "big") for e in range(0, 64, 4)] + ([0] * 48)

            #构造64个word
            for j in range(16, 64):
                W[j] = (W[j - 16] + (
                            self.rightrotate(W[j - 15], 7) ^ self.rightrotate(W[j - 15], 18) ^ (W[j - 15] >> 3)) + W[
                            j - 7] + (self.rightrotate(W[j - 2], 17) ^ self.rightrotate(W[j - 2], 19) ^ (
                            W[j - 2] >> 10))) & ((2**32)-1)

            A, B, C, D, E, F, G, H = digest

            for j in range(64):
                A, B, C, D, E, F, G, H = self.Compress(W[j], self.constants[j], A, B, C, D, E, F, G, H)

        return "".join(format(h, "02x") for h in b"".join(
            d.to_bytes(4, "big") for d in [(x + y) & ((2**32)-1) for x, y in zip(digest, (A, B, C, D, E, F, G, H))]))


def main():
    encoder = SHA256()

    while True:
        message = input("Enter string: ")
        print(f"Output: {encoder.hash(message)}\n")


if __name__ == "__main__":
    main()

参考文献

SHA-2 wiki