图处理系列 (一)--网络生成与图入度计算

图论和网络科学都会涉及到大量对图的特性的统计计算，一般将与图数据相关的统计、挖掘、可视化统称为图处理。本系列文章主要希望探讨多方面的图处理理论与方法，包括图的统计性质、表示方法、计算算法、计算模型以及基于图论的数据挖掘等内容。文章只有在必要的情况下区分图和网络的概念，所以文章术语中的图与网络将混用。

 1.图处理引擎

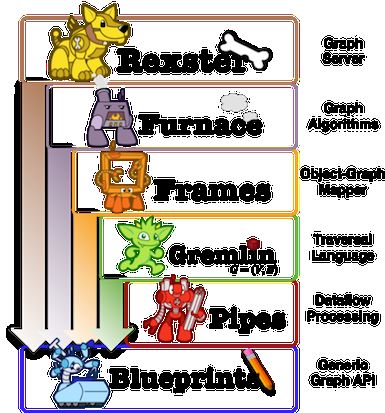
目前通用的图处理软件主要包括两种。一种主要基于遍历算法、实时的图数据库，如 Neo4j , OrientDB , DEX , 和 InfiniteGraph .另一种则是以图顶点为中心的消息传递批处理的并行引擎，如Hama , Golden Orb , Giraph , 和 Pregel .前者基本都基于tinkerpop的图基础框架，tinkerpop项目关系如图1所示：

图1 thinkerpop项目框架

其后者则主要是基于BSP模型所实现的并行图处理包。BSP是由哈佛大學Viliant和牛津大學Bill McColl提出的并行计算模型。一个BSP模型由大量相互关联的处理器(processor)所组成，它们之间形成了一个通信网络。每个处理器都有快速的本地内存和不同的计算线程。一次BSP计算过程包括一系列全局超步组成，超步就是计算中一次迭代。每个超步主要包括三个组件：

1. 并发计算(Concurrent computation)：每个参与的处理器(processor)都有自身的计算任务，它们只读取存储在本地内存的值。这些计算都是异步并且独立的。
2. 通讯(Communication): 处理器群相互交换数据，交换的形式：由一方发起推送(put)和获取(get)操作。
3. 栅栏同步(Barrier synchronisation): 当一个处理器遇到路障，会等到其他所有处理器完成它们的计算步骤。每一次同步也是一个超步的完成和下一个超步的开始。

 2.网络生成

现实世界的复杂网络包括无标度网络(Scale-free Network)、随机网络(Random Network)，依赖网络(Dependency network)等。其中无标度网络是由匈牙利物理学家Albert-László Barabási在绘制互联网拓扑的研究中所提出的概念，他发现随机网络(社会、生物网络)中一些节点(hubs)有比其它节点更多的连接，从而整个网络服从幂次定律(power-law)分布。于是Barabási和Albert提出了无标度网络的生成机制--“优先连接”，用于解释幂次定律分布的现象。因而优先连接算法生成的网络能够模拟现实世界的网络，我们采用R来实现BA 模型的网络生成，采用的igraph包。

igraph是一个开源的图(有向、无向图)生成和操作的类库，它底层由C实现，并实现了python, R语言的发行包，覆盖全平台(linux,window,MacOS)。它能够生成正则图(regular  graphs)、随机图(random graphs)等,能给顶点和边赋值，还可以计算不同的结构属性、图同构等。igraph支持的格式包括:Edge list,Pajek,GraphML等。Edge list是简单的txt文件，使用顶点id来定义边。GraphML基于XML，用来存储图的边和顶点属性。更多的格式内容请参考igraph帮助文档。用法如下所示：

barabasi.game(n, power = 1, m = NULL, out.dist = NULL, out.seq = NULL,

    out.pref = FALSE, zero.appeal = 1, directed = TRUE,

    algorithm = c("psumtree", "psumtree-multiple", "bag"),

    start.graph = NULL)

power: 优先连接的幂，默认为1.即线性优先连接。m:数值常数，这个值控制每次时间步长添加的边。只有在 out.dist 和 out.seq都为空的时候生效。无标度网络生成的R代码如下：

> library("igraph")

> g <- simplify(barabasi.game(100000, m=10))

> length(V(g))

[1] 100000

> length(E(g))

[1] 999945

> E(g)[1:5]

Edge sequence:



[1] 2 -> 1

[2] 3 -> 1

[3] 3 -> 2

[4] 4 -> 1

[5] 4 -> 2

> write.graph(g, '/tmp/barabasi.xml', format='graphml')

barabasi.game()函数，生成ba模型的无标度网络，每次添加的边为10(m=10).write.graph()函数将生成的网络以graphml的格式保存在磁盘中。

3.图入度计算

顶点的度(degree)是图最基本的结构，是指与它关联的边的数量。有向图会区分入度(in-degree)和出度(out-degree).图的度分布(degree distribution)是所有顶点的概率分布。igraph中只需要使用degree函数可以计算顶点的度，用法如下所示：

degree(graph, v=V(graph), mode = c("all", "out", "in", "total"),

       loops = TRUE, normalized = FALSE)

degree.distribution(graph, cumulative = FALSE, ...)

我们通过改变图生成算法的幂，观察图的入度分布。R代码如下：

library(igraph)



g <- barabasi.game(100000)

d <- degree(g, mode="in")

dd <- degree.distribution(g, mode="in", cumulative=TRUE)

alpha <- power.law.fit(d, xmin=20)

plot(dd, log="xy", xlab="degree", ylab="cumulative frequency",

     col=1, main="Nonlinear preferential attachment")

lines(10:500, 10*(10:500)^(-coef(alpha)+1))



powers <- c(0.9, 0.8, 0.7, 0.6)

for (p in seq(powers)) {

  g <- barabasi.game(100000, power=powers[p])

  dd <- degree.distribution(g, mode="in", cumulative=TRUE)

  points(dd, col=p+1, pch=p+1)

}



legend(1, 1e-5, c(1,powers), col=1:5, pch=1:5, ncol=1, yjust=0, lty=0)

结果如下图所示：

本作品由VentLam创作，采用知识共享署名-非商业性使用-相同方式共享 2.5 中国大陆许可协议进行许可。