菜鸟刷题Day7
一.整理字符串:1544. 整理字符串 - 力扣(LeetCode)
描述
给你一个由大小写英文字母组成的字符串 s 。
一个整理好的字符串中,两个相邻字符 s[i] 和 s[i+1],其中 0<= i <= s.length-2 ,要满足如下条件:
若 s[i] 是小写字符,则 s[i+1] 不可以是相同的大写字符。
若 s[i] 是大写字符,则 s[i+1] 不可以是相同的小写字符。
请你将字符串整理好,每次你都可以从字符串中选出满足上述条件的 两个相邻 字符并删除,直到字符串整理好为止。
请返回整理好的 字符串 。题目保证在给出的约束条件下,测试样例对应的答案是唯一的。
注意:空字符串也属于整理好的字符串,尽管其中没有任何字符。
示例 1:
输入:s = "leEeetcode"
输出:"leetcode"
解释:无论你第一次选的是 i = 1 还是 i = 2,都会使 "leEeetcode" 缩减为 "leetcode" 。
解题思路
这个题目描述很长给人一种压迫感,但是这个题目并不难。对于删除字符,我们至少有两种办法一种是直接挪动数据(复杂度太高,不考虑),还有就是新开一个数组,将有效数据放入新的数组中(用空间换时间)。
这里采用栈的思想,新建一个数组通过下标控制来达到模拟实现栈的目标。用栈的话就会很简单,直接将元素读取到栈中,如果栈顶的两个相邻元素是互为大小写,那么直接将栈顶的两个元素删除就行。在数组的表现形式上就是不断尾插尾删
char * makeGood(char * s)
{
int len=strlen(s);
char*tmp=(char*)malloc(sizeof(char)*(len+1));
int top=0;//栈顶位置
for(int i=0;i<len;i++)
{
//将所有元素入栈,如果栈顶的两个元素互为大小写,就将两个元素都删除
tmp[top++]=s[i];
if(top>=2&&(tmp[top-1]==tmp[top-2]-32||tmp[top-1]==tmp[top-2]+32))
{
//因为top是后置++,新入栈的两个元素一定是top-1和top-2
top-=2;//改变top位置就实现删除,这个在数组中常用的(逻辑覆盖删除)
}
}
//字符串的结束标志是'\0',前面的循环到'\0'前就结束了,所以还需要我们自行补充
tmp[top]='\0';
return tmp;
}
二.开幕式火焰:LCP 44. 开幕式焰火 - 力扣(LeetCode)
描述
「力扣挑战赛」开幕式开始了,空中绽放了一颗二叉树形的巨型焰火。
给定一棵二叉树 root 代表焰火,节点值表示巨型焰火这一位置的颜色种类。请帮小扣计算巨型焰火有多少种不同的颜色。
示例 1:
输入:
root = [1,3,2,1,null,2]输出:
3解释:焰火中有 3 个不同的颜色,值分别为 1、2、3
提示:
1 <= 节点个数 <= 10001 <= Node.val <= 1000
解题思路
根据示例可以看到,如果树中出现值相同的节点也只算一次,也就是说要统计节点val不相同的个数(null不算),有没有想起一个很熟悉的解法,这个解法在刚开始的时候就已经提到过了,就是基数排序。
其实就是建立一个数组,然后将节点的值作为下标,然后给这个下标位置的元素+1(要知道如果不对变量初始化,则变量中的值是随机值,所以一定要初始化)用memset对数组初始化后,调用前序遍历,最后再对数组遍历统计数组中不为零的个数。
int hash[1001];//因为前序遍历中也要用到这个数组,所以写成全局变量
void Perfind(struct TreeNode*root)
{
if(root)
{
hash[root->val]+=1;//是不是很眼熟哈哈
Perfind(root->left);
Perfind(root->right);
}
}
int numColor(struct TreeNode* root)
{
memset(hash,0,sizeof(hash));
Perfind(root);
int count=0;
//暴力遍历
for(int i=0;i<1001;i++)
{
if(hash[i]!=0)
count++;
}
return count;
}
你猜我为什么不直接在声明的时候定义写成:int hash[1001]={0},当然是因为跑不过所以才用memset。
三.从根到叶的二进制数之和:1022. 从根到叶的二进制数之和 - 力扣(LeetCode)
描述
给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。
例如,如果路径为 0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数 01101,也就是 13 。
对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。
返回这些数字之和。题目数据保证答案是一个 32 位 整数。
示例1:
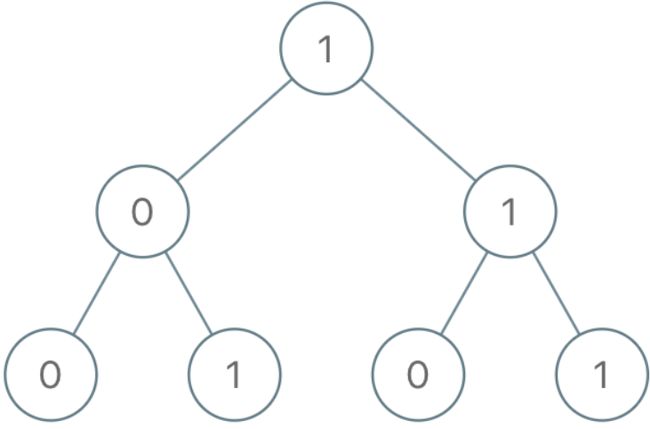
输入:root = [1,0,1,0,1,0,1]
输出:22
解释:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
解题思路
关于二进制求和的题目在前面也有做过,当时给了两种方法,但是第一种在这里不太好用,这里建议使用左移操作符,求和不是问题。
根据题目给的示例可以发现,是先走完左子树再走的右子树,也就是说遍历顺序是左子树——右子树——根(后序遍历),所以只要递归使用后续遍历即可,遍历到叶子节点时就开始计算累加和。当然如果这是一个空树,那我们直接返回空就行。
void AddVal(struct TreeNode* root,int val,int *sum)
{
if(root==NULL)
return NULL;
//树不为空树,直接开始计算本次遍历获取到的二进制数
val=(val<<1)+root->val;
//到达叶子节点就累加计算整棵树的结果
if(root->left==NULL&&root->right==NULL)
*sum+=val;
//递归遍历
AddVal(root->left,val,sum);
AddVal(root->right,val,sum);
}
int sumRootToLeaf(struct TreeNode* root)
{
int sum=0;
AddVal(root,0,&sum);
return sum;//最后sum就是结果
}
四.二叉树的坡度:563. 二叉树的坡度 - 力扣(LeetCode)
描述
给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
示例1:
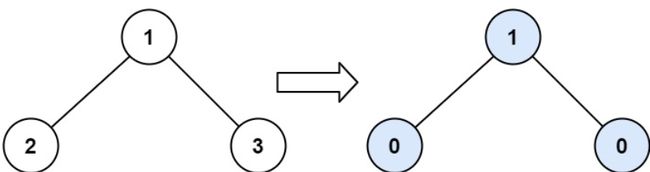
输入:root = [1,2,3]
输出:1
解释:
节点 2 的坡度:|0-0| = 0(没有子节点)
节点 3 的坡度:|0-0| = 0(没有子节点)
节点 1 的坡度:|2-3| = 1(左子树就是左子节点,所以和是 2 ;右子树就是右子节点,所以和是 3 )
坡度总和:0 + 0 + 1 = 1
解题思路
这一题其实是一个变种的二叉树遍历,二叉树的坡度等于左树的坡度加右数的坡度加根的坡度,最后根节点的坡度是根所有子树和之间的坡度。可以采取和上题类似的办法,从叶子节点开始计算坡度和子树的和,并且累加每个子树坡度。最后根节点的坡度用两个子树和相减.
int dfs(struct TreeNode*root,int *sum)
{
if(root==NULL)
return 0;
int left=dfs(root->left,sum);
int right=dfs(root->right,sum);
*sum+=abs(left-right);//拿到两个节点之间差的绝对值
return left+right+root->val;//题目中说是该节点的左子树之和和右子树之和的差,要知道该节点的左子树又有左子树和右子树,所以必须要将左右子树节点记下来
}
int findTilt(struct TreeNode* root)
{
int sum=0;
dfs(root,&sum);
return sum;
}
该说不说,递归有时候可读性是真不高,也很难整(菜鸡流泪again)。
人们总是高估短期努力带来的提升,而忽略长期坚持带来的改变。今天是第七天了,你还有坚持吗?