七大排序 (插入,希尔,选择,冒泡,堆,快排,归并)
目录
排序 : 所谓排序就是使一串无序的数据进行排序后,变为递增或递减的数列.
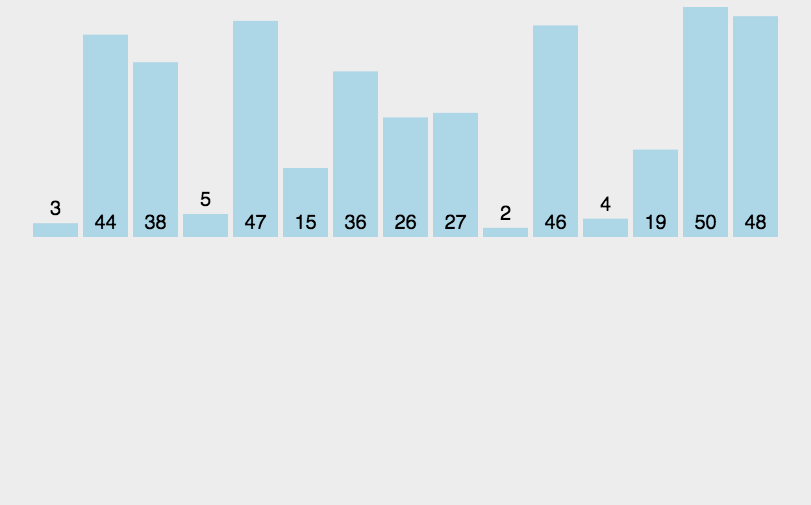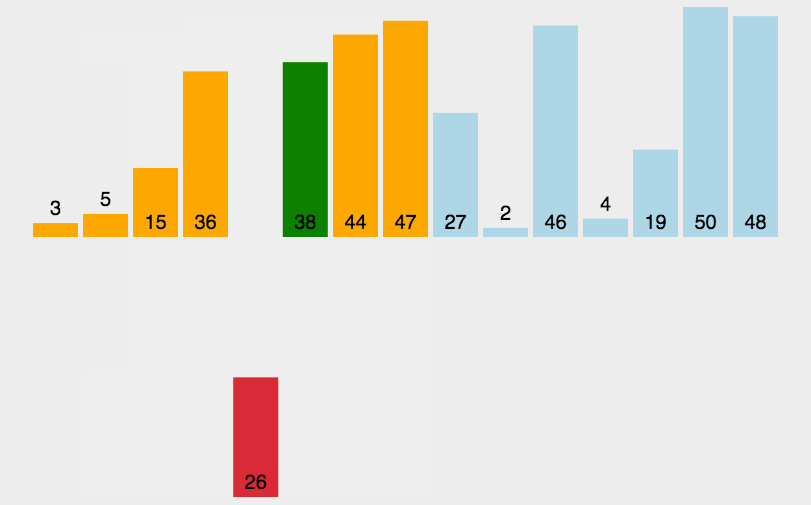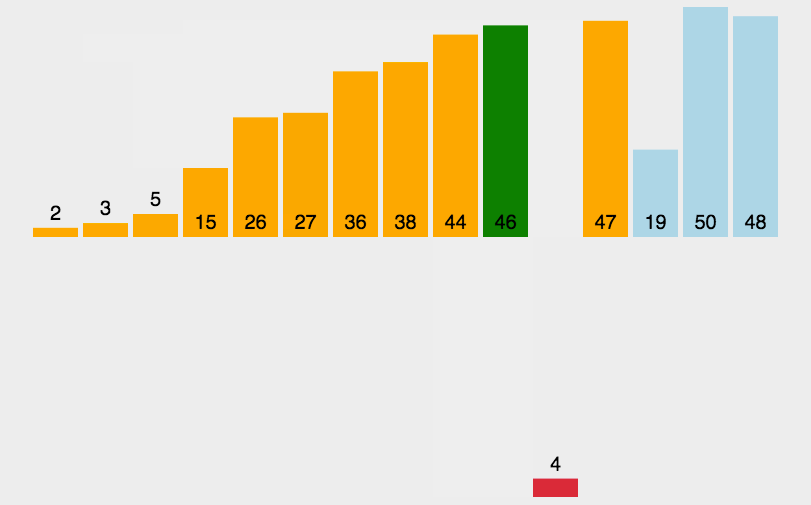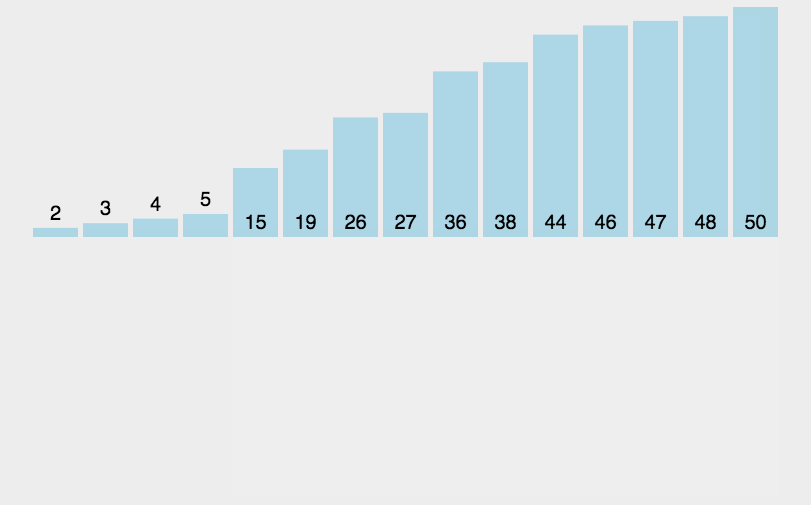
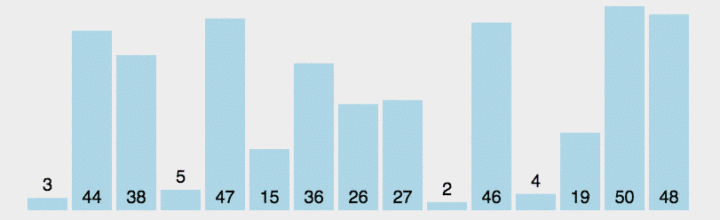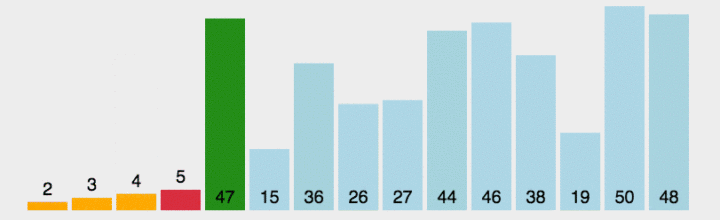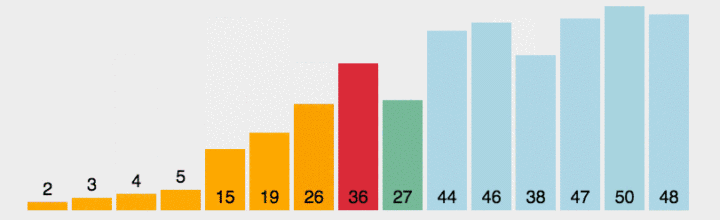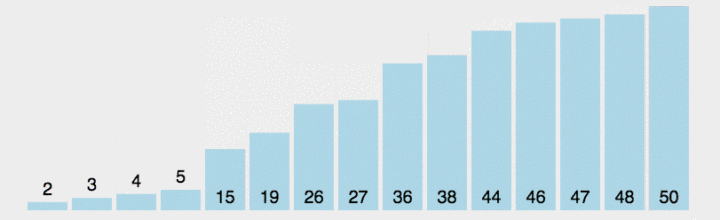
稳定性 : 若有一组数据 : (为了看出效果,我加了一个标识符 a 与 b)编辑
编辑
一. 插入排序 (直接插入排序)
二 . 希尔排序
三 . 选择排序
四 . 冒泡排序
五 . 堆排序
六 . 快速排序
七 . 归并排序
排序 : 所谓排序就是使一串无序的数据进行排序后,变为递增或递减的数列.
稳定性 : 若有一组数据 : (为了看出效果,我加了一个标识符 a 与 b)
我们可以看出第一幅图排序后 : 相同的两个数字5它们的前后顺序还是原来的顺序(a下标的5 还是在 b下标5的前面). 这是我们就认为它是一个稳定的排序
但是第二幅图排序后 : (b下标的5 在 a下标5的前面). 这是我们就认为它是不稳定的排序.
常见的排序有以下几种 : 直接插入排序,希尔排序,选择排序,堆排序,冒泡排序,快速排序,归并排序.
一. 插入排序 (直接插入排序)
插入排序的基本思想 :
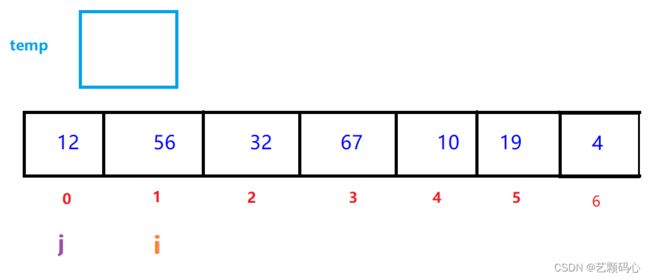
接下来我用画图来具体演示一下它是如何进行排序的 :
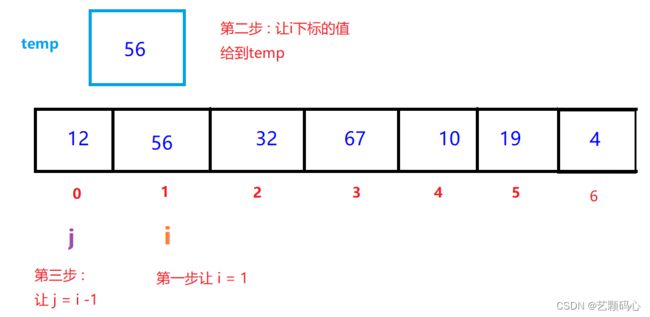
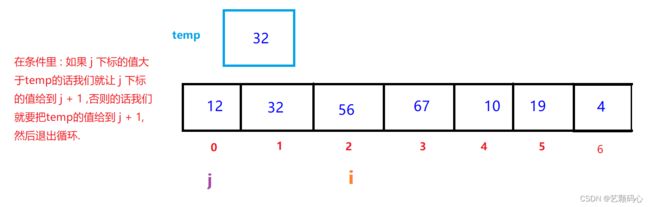
首先我们先定义两个下标 : i j
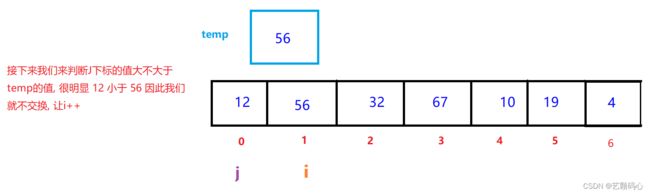
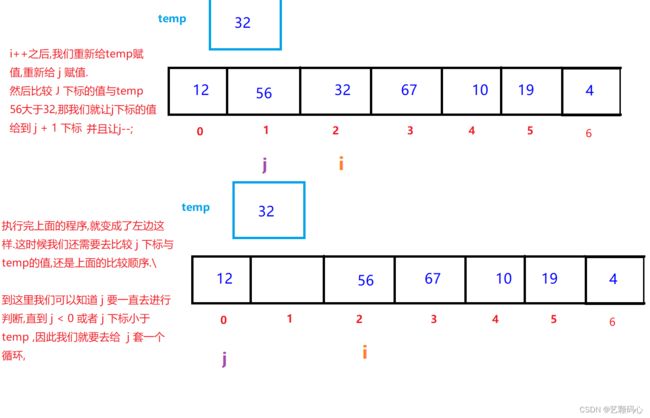
让 i 从1下标开始往后走. 把 i 下标的值给到 temp ; 让 j 每次都等于 i - 1,然后比较 j 下标的值 与 temp的值 ; 如果符合条件(具体情况看要排递减的还是要递增),那么就让 j 下标的值给到 j + 1下标,
然后让 j-- , 再重复比较 , 直到不符合条件,就退出比较,让i++进行下一轮比较.
这里我们排一个递增的数列(从小到大)
经过上面的分析 : 我们可以写出一下代码 :
public void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
for (int j = i - 1; j >= 0; j--) {
if (array[j] > temp) {
array[j + 1] = array[j];
} else {
array[j + 1] = temp;
break;
}
}
}
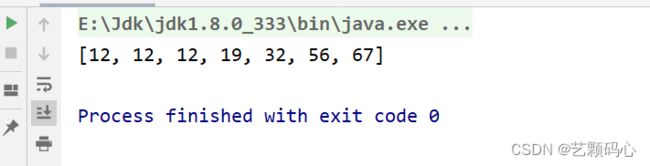
}但是结果确实不尽人意的,问题在这 :
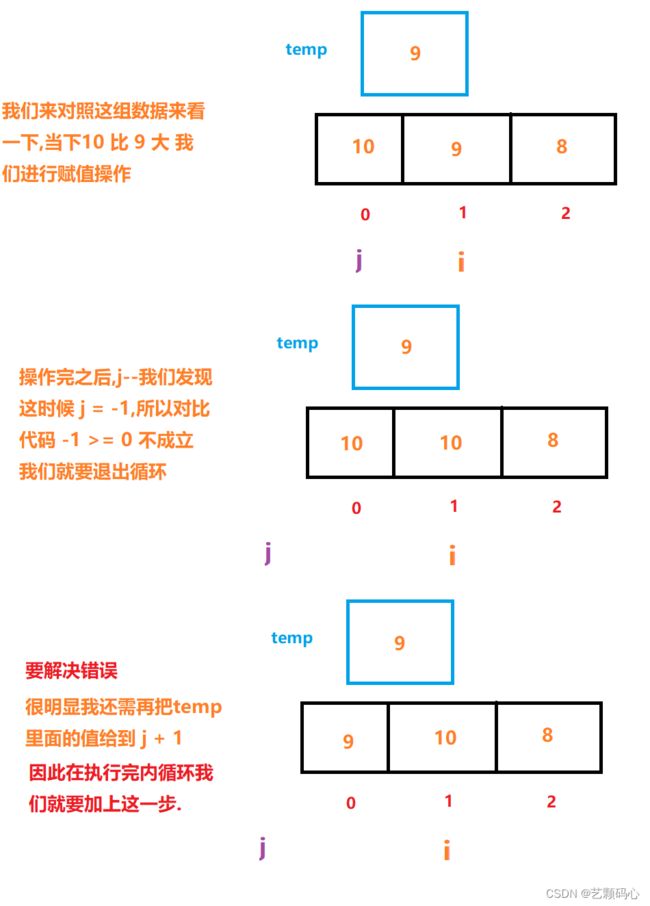
综上 得出新的代码 :
public void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i - 1;
for (; j >= 0; j--) {
if (array[j] > temp) {
array[j + 1] = array[j];
} else {
array[j + 1] = temp;
break;
}
}
array[j + 1] = temp;
}
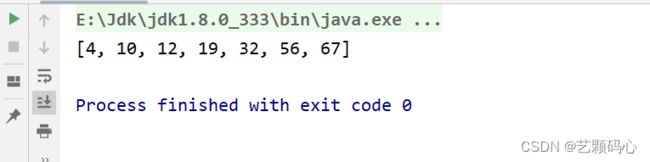
}插入排序的时间复杂度 : O(n^2)
空间复杂度 : O(1)
稳定性 : 稳定
插入排序的优点在于如果数据趋于有序的情况下,那么插入排序会更快.
这就是插入排序了!!!!!
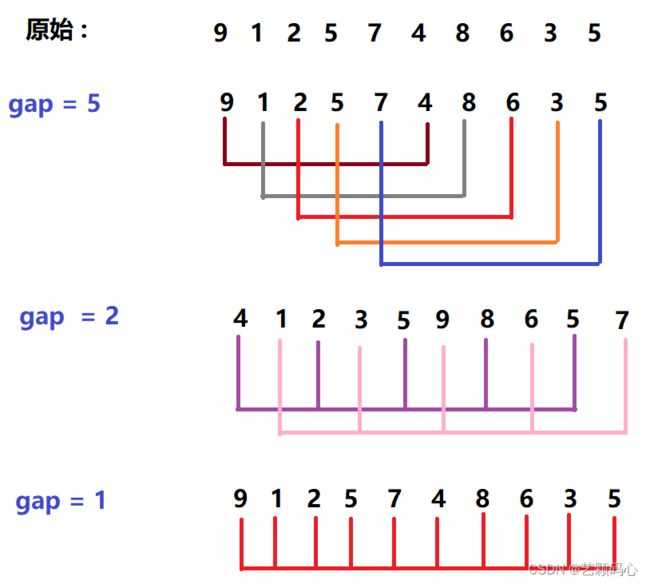
二 . 希尔排序
希尔排序就是对直接插入排序的优化.
它的排序方法就是把一组数分为多个组.
例如 : 把它先分为5组 然后让他们每组进行插入排序,这样每组内的数就是有序了
然后再分为2组 然后让他们每组进行插入排序
最后整体看做是一组 然后进行插入排序
这样的话就会有个问题,分组我们怎么去分,最官方的解释 : 就是到目前为止还没有一个公式可以去计算分多少组最合适.因此我们分组的话,让gap的初始值等于数组的长度除以2,接下来每次组内比较完之后,再让 gap = gap / 2,直到 gap == 1 整体看做一组进行插入排序.
/**
* 希尔排序
* 时间复杂度 : O(n^1.3)
* 空间复杂度 : O(1)
* @param array
*/
public void shellSort(int[] array) {
int gap = array.length / 2;
while (gap > 0) {
shell(array,gap);
gap = gap / 2;
}
}
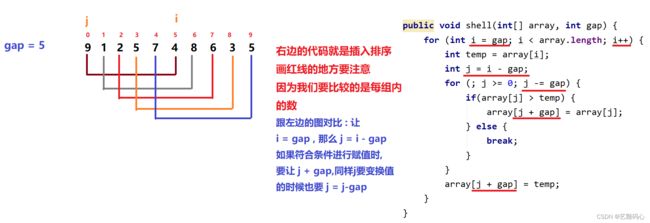
public void shell(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int temp = array[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if(array[j] > temp) {
array[j + gap] = array[j];
} else {
break;
}
}
array[j + gap] = temp;
}
}希尔排序的时间复杂度 : O(n ^ 1.3)
空间复杂度 : O(1)
稳定性 : 不稳定
这就是希尔排序了!!!!
三 . 选择排序
基本思想 :
/**
* 选择排序
* 时间复杂度 : O(n^2)
* 空间复杂度 : O(1)
* 稳定性 : 不稳定
*/
public void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array,i,minIndex);
}
}
//交换
public void swap (int[] array, int x, int y) {
int temp = array[x];
array[x] = array[y];
array[y] = temp;
}选择排序也可以进行优化 : 上面的每次遍历数组后只能得到一个最小值的下标, 我们可以 再加一个最大值的下标.这样每次内循环之后我们就可以确定两个下标的值.
//选择排序的优化
public void selectSort(int[] array) {
for (int left = 0, right = array.length - 1; left < right; left++, right--) {
int minIndex = left;
int maxIndex = right;
for (int j = left; j <= right; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
if (array[j] > array[maxIndex]) {
maxIndex = j;
}
}
swap(array,minIndex,left);
if (maxIndex == left) {
maxIndex = minIndex;
}
swap(array,maxIndex,right);
}
}
//交换
public void swap (int[] array, int x, int y) {
int temp = array[x];
array[x] = array[y];
array[y] = temp;
}选择排序的时间复杂度 : O(n^2)
空间复杂度 : O(1)
稳定性 : 不稳定
以上就是选择排序!!!.
四 . 冒泡排序
由上面的动图,每次遍历一次数组后就会确定一个最大或者最小的值.
//冒泡排序
public void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
boolean flag = true;
for (int j = 0; j < array.length - 1 - i; j++) {
if (array[j + 1] < array[j]) {
swap(array,j+1,j);
flag = false;
}
}
if (flag) {
break;
}
}
}
//交换
public void swap (int[] array, int x, int y) {
int temp = array[x];
array[x] = array[y];
array[y] = temp;
}冒泡排序的时间复杂度 : O(n^2)
空间复杂度 : O(1)
稳定性 : 稳定
以上就是冒泡排序了!!!
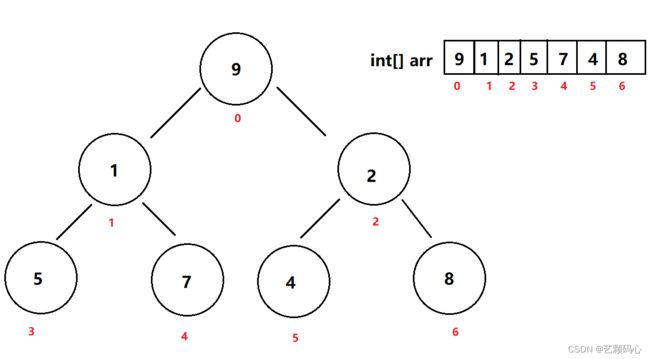
五 . 堆排序
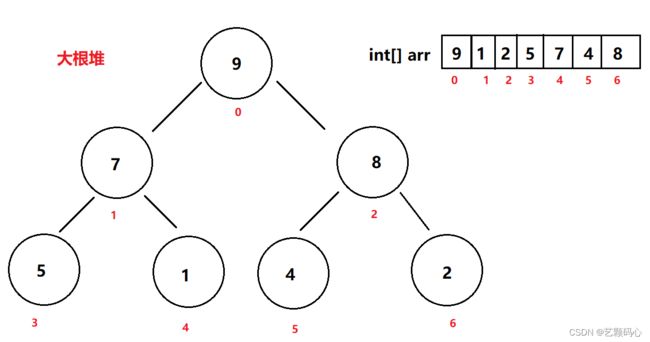
因为我们要排升序因此我们就先要把下面这个堆建成大根堆
通过向下调整 建大根堆:
//建堆(使用向下调整建堆的时间复杂度为O(n))
public void createHeap(int[] array) {
for (int parent = (array.length - 1 -1) / 2; parent >= 0; parent--) {
shiftDown(array,parent,array.length - 1);
}
}
//向下调整 (时间复杂度 : O(logn))
public void shiftDown(int[] array, int parent, int end) {
int child = parent * 2 + 1;
while (child <= end) {
if ((child + 1 <= end) && (array[child + 1] > array[child])) {
child++;
}
if (array[parent] < array[child]) {
swap(array,parent,child);
parent = child;
child = parent * 2 + 1;
} else {
break;
}
}
}
//交换
public void swap (int[] array, int x, int y) {
int temp = array[x];
array[x] = array[y];
array[y] = temp;
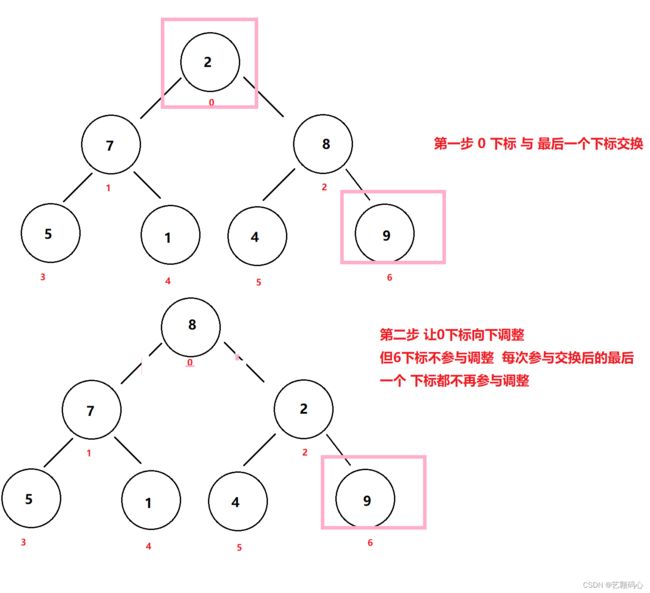
}每次让0下标跟最后一个下标交换,交换完之后最后一个下标就不再参与调整.然后再把0下标向下调整确保它是一个大根堆.
/**
* 堆排序
* 时间复杂度 : O(nlogn)
* 空间复杂度 : O(1)
* 稳定性 : 不稳定
* @param array
*/
public void heapSort(int[] array) {
for (int i = array.length - 1; i > 0; i--) {
swap(array,0,i);
shiftDown(array,0,i - 1);
}
}
//向下调整 (时间复杂度 : O(logn))
public void shiftDown(int[] array, int parent, int end) {
int child = parent * 2 + 1;
while (child <= end) {
if ((child + 1 <= end) && (array[child + 1] > array[child])) {
child++;
}
if (array[parent] < array[child]) {
swap(array,parent,child);
parent = child;
child = parent * 2 + 1;
} else {
break;
}
}
}
//交换
public void swap (int[] array, int x, int y) {
int temp = array[x];
array[x] = array[y];
array[y] = temp;
}
堆排序的时间复杂度 : O(nlogn)
空间复杂度 :O(1)
稳定性 : 不稳定
以上就是堆排序!!!
六 . 快速排序
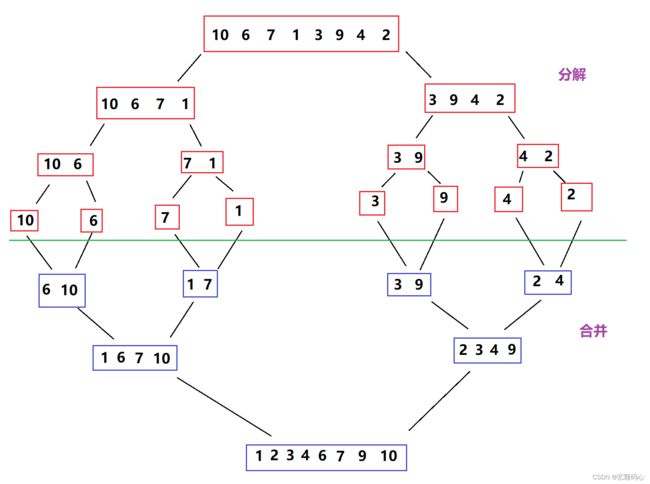
快速排序就是去重复这个步骤.递归左边和右边
/**
* 快速排序
* 时间复杂度 : O(nlogn)
* 空间复杂度 : O(logn)
* 稳定性 : 不稳定
* @param array
*/
public void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
public void quick(int[] array, int s, int e) {
if (s >= e) {
return;
}
int pivot = partition(array,s,e);
//递归左边
quick(array,0,pivot - 1);
//递归右边
quick(array,pivot + 1,e);
}
//挖坑法 ----> 找基准值(pivot)
public int partition(int[] array, int left, int right) {
int temp = array[left];
while (left < right) {
if (left < right&& array[right] >= temp) {
right--;
}
array[left] = array[right];
if (left < right && array[left] <= temp) {
left++;
}
array[right] = array[left];
}
array[left] = temp;
return left;
}快速排序的优化 :
如果是一组有序的数列(1,2,3,4,5,6,7,8) 在这种情况下我们去找基准每次都会是第一个数.
那么递归的话永远都是右边递归,这样也就会形成单分支的情况 时间复杂度就会变成O(n^2)
空间复杂度 : O(n) , 为了避免单分支的情况,我们可以在设标准值的时候去改变一下.三数取中法
: 去判断三个数 最左边的 中间的 最右边的 . 拿出这三个数的第二大值(也就是不要最大的值,也不要最小的值,就取中间的那个数), 然后让它与0下标去交换,然后再去找基准.
public void quick(int[] array, int s, int e) {
if (s >= e) {
return;
}
//三数取中法 避免单分支的情况
int mid = findMid(array,s,e);
swap(array,s,mid);
int pivot = partition(array,s,e);
//递归左边
quick(array,0,pivot - 1);
//递归右边
quick(array,pivot + 1,e);
}
//找到第二大值
public int findMid(int[] array, int s, int e) {
int mid = s + (e - s) / 2;
if (array[s] < array[e]) {
if (array[mid] > array[e]) {
return e;
} else if (array[mid] < array[s]) {
return s;
} else {
return mid;
}
} else {
if (array[mid] > array[s]) {
return s;
} else if (array[mid] < array[e]) {
return e;
} else {
return mid;
}
}
}快速排序的再优化 :
如果数据有很多 : 假设有100000个数,那么一直递归下去,它会变成几乎有序的数组,那么我们就可以采用插入排序.
可以设一个阈值 : 当 s - e == 10时 我们就去让它去进行插入排序.(因为插入排序在越有序的数组下它的时间复杂度越低).
public void quick(int[] array, int s, int e) {
if (s >= e) {
return;
}
if (s - e <= 15) {
insertSort(array,s,e);
return;
}
//三数取中法 避免单分支的情况
int mid = findMid(array,s,e);
swap(array,s,mid);
int pivot = partition(array,s,e);
//递归左边
quick(array,0,pivot - 1);
//递归右边
quick(array,pivot + 1,e);
}
//为快速排序服务的直接插入排序
public void insertSort(int[] array, int s, int e) {
for (int i = s; i <= e; i++) {
int temp = array[i];
int j = i - 1;
for (; j >= 0; j--) {
if (array[j] > temp) {
array[j + 1] = array[j];
} else {
array[j + 1] = temp;
break;
}
}
array[j + 1] = temp;
}
}经过以上两种优化那么快速排序的速度只会更快!!!!!
快速排序的时间复杂度 : O(nlogn)
空间复杂度 : O(logn)
稳定性 : 不稳定
以上就是快速排序了!!!!!
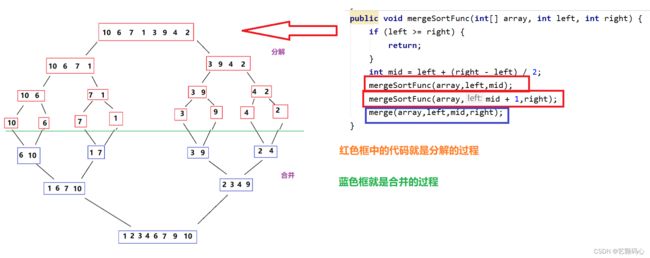
七 . 归并排序
/**
* 归并排序
* 时间复杂度 : O(n*logn)
* 空间复杂度 : O(n)
* 稳定性 : 稳定
* @param array
*/
public void mergeSort(int[] array) {
mergeSortFunc(array,0,array.length - 1);
}
public void mergeSortFunc(int[] array, int left, int right) {
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
mergeSortFunc(array,left,mid);
mergeSortFunc(array,mid + 1,right);
merge(array,left,mid,right);
}
public void merge(int[] array, int start, int mid, int end) {
int s1 = start;
int s2 = mid + 1;
int[] tmp = new int[end - start + 1];
int k = 0;
while (s1 <= mid && s2 <= end) {
if (array[s1] > array[s2]) {
tmp[k++] = array[s2++];
} else {
tmp[k++] = array[s1++];
}
}
while (s1 <= mid) {
tmp[k++] = array[s1++];
}
while (s2 <= end) {
tmp[k++] = array[s2++];
}
for (int i = 0; i < tmp.length; i++) {
array[start + i] = tmp[i];
}
}归并排序的时间复杂度 : O(n*logn)
空间复杂度 : O(n)
稳定性 : 稳定
以上就是归并排序了!!!
到这里七大排序就全部结束了!
希望可以帮助到大家,如果什么疑问的话,可以私信我~~~~~~~
目录
排序 : 所谓排序就是使一串无序的数据进行排序后,变为递增或递减的数列.
稳定性 : 若有一组数据 : (为了看出效果,我加了一个标识符 a 与 b)编辑
编辑
一. 插入排序 (直接插入排序)
二 . 希尔排序
三 . 选择排序
四 . 冒泡排序
五 . 堆排序
六 . 快速排序
七 . 归并排序