【c++】:“无敌的适配器来咯“栈和队列模拟实现以及优先级队列的模拟实现。
文章目录
- 前言
- 一.栈和队列的模拟实现
- 二.优先级队列
- 总结
前言
栈的介绍和使用:
一、栈和队列的模拟实现
容器适配器:
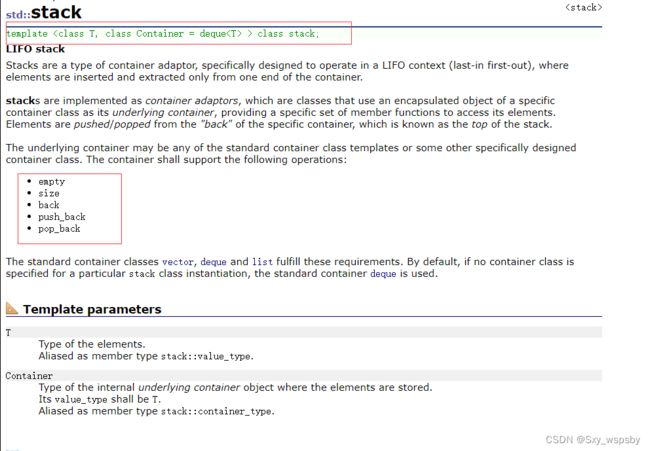
前面我们说过stack和queue是一种容器适配器,同样也是作为容器适配器被实现的,所以我们可以直接使用一个公共的容器来当stack的适配器,适配器是用来转换的,将已有的东西进行转换,比如将vector当我们栈的容器实现栈的功能,我们先看一下库中如何描述栈的:
可以看到库中是用的deque来当stack的容器,并且stack的接口非常简单,所以我们现在就开始实现:
#include
#include
using namespace std;
namespace sxy
{
template>
class stack
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
T& top()
{
return _con.back();
}
const T& top() const
{
return _con.back();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
private:
Container _con;
};
void test3()
{
stack st;
st.push(1);
st.push(2);
st.push(3);
st.push(4);
while (!st.empty())
{
cout << st.top() << " ";
st.pop();
}
}
} 因为我们要使用vector做适配器所以包含了vector的头文件,然后我们所有的函数直接使用容器的公共接口即可,比如vector的push_back等等。在模板中我们用了vector的缺省容器,如果你不想用vector,你也可以使用list作为stack的容器,只需要:stack
void push(const T& x)
{
_con.push_back(x);
}对于push我们直接使用容器的尾插即可。
void pop()
{
_con.pop_back();
}对于pop直接使用尾删即可,因为栈本来就是后进先出的。
T& top()
{
return _con.back();
}
const T& top() const
{
return _con.back();
}top是返回栈顶元素,容器中的back()接口返回的就是栈顶元素。
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}size()和empty与上述同理,都使用容器的公共接口就能解决。
队列的模拟实现
我们先看一下库中的实现,同样也是用deque作为queue的容器。
在这里我们要说明一下,由于vector的头删效率极低,所以vector是不能作为queue的容器的。这里可以用list作为queue的容器,也可以用deque作为queue的容器。第一步是创建一个容器的对象_con.
#include
#include
using namespace std;
namespace sxy
{
template>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
T& front()
{
return _con.front();
}
const T& front() const
{
return _con.front();
}
T& back()
{
return _con.back();
}
const T& back() const
{
return _con.back();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
private:
Container _con;
};
void test2()
{
queue qe;
qe.push(1);
qe.push(2);
qe.push(3);
qe.push(4);
while (!qe.empty())
{
cout << qe.front() << " ";
qe.pop();
}
}
} 队列的实现与栈不同的是队尾插入队头出,所以对于pop接口和top接口而言是不一样的:
void pop()
{
_con.pop_front();
}队列要头删所以用头删的接口。
T& front()
{
return _con.front();
}
const T& front() const
{
return _con.front();
}
T& back()
{
return _con.back();
}
const T& back() const
{
return _con.back();
}这里提供了队头元素的返回和队尾元素的返回,因为库中也是实现的。
这样栈和队列的模拟实现就完成了,对于栈和队列我们只需要明白适配器的使用,只要学到了这个后面很多的实现都变简单了。
二、优先级队列
什么是优先级队列呢?
下面我们来看看库中的优先级队列:

 我们可以看到优先级队列的实现除了容器外还多了一个Compare,这个是什么呢?这个其实是一个仿函数,这里的仿函数是来解决优先级队列是小的优先级高还是大的优先级高,我们默认是大的优先级高也就是大堆。
我们可以看到优先级队列的实现除了容器外还多了一个Compare,这个是什么呢?这个其实是一个仿函数,这里的仿函数是来解决优先级队列是小的优先级高还是大的优先级高,我们默认是大的优先级高也就是大堆。
#include
using namespace std;
#include
namespace sxy
{
template
struct less
{
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
template
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
template,class Compare = less>
class priority_queue
{
public:
void adjust_up(int child)
{
Compare com;
size_t parent = (child - 1) / 2;
while (child > 0)
{
//if (_con[parent] < _con[child])
if (com(_con[parent],_con[child]))
{
swap(_con[parent], _con[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void adjust_down(int parent)
{
Compare com;
size_t child = 2 * parent + 1;
while (child < _con.size())
{
//if ((child + 1) < _con.size() && _con[child] < _con[child + 1])
if ((child+1)<_con.size()&&com(_con[child],_con[child+1]))
{
++child;
}
//if (_con[parent] < _con[child])
if (com(_con[parent],_con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size() - 1);
}
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
T& top()
{
return _con.front();
}
const T& top() const
{
return _con.front();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
private:
Container _con;
};
void test1()
{
priority_queue pq;
pq.push(1);
pq.push(16);
pq.push(14);
pq.push(19);
pq.push(17);
pq.push(12);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
}
} 第一步是创建一个容器的对象_con.
我们一个函数一个函数依次来分析:
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size() - 1);
}首先是push,由于优先级队列本质还是一个队列,所以遵循先进先出的原则。插入的时候在队尾插入即可,这个时候我们不能结束,因为要排优先级,所以我们要将最后插入的这个数依次向前调整。听到这里是不是很熟悉呢?没错!这其实就是我们之前讲过的堆,而这个adjust_up函数也和我们当时实现的向上调整一模一样,所以在这里我们就不在详细的介绍如何调整了,具体的可以去看我的那篇关于堆的文章。
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}对于一个已经排好序的队列我们是不可以直接出数据的,为了保证数据的有序性我们先讲第一个元素和最后一个元素交换,这样我们就把要删除的第一个队顶元素移到了队尾,然后直接尾删就删掉了原先的队头元素,刚刚我们将最后一个元素换到了对头,所以我们要让对头这个数据依次向下调整来保持有序性。
T& top()
{
return _con.front();
}
const T& top() const
{
return _con.front();
}由于优先级队列只提供对头元素的返回所以我们只用容器的front接口即可。
想要看明白向上调整接口需要先介绍一下仿函数:
template
struct less
{
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
template
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
}; 我们可以看到仿函数的实现其实就是创建一个类然后里面封装一个()的运算符重载,比如我们的less小于,对于一个数是否小于另一个数我们可以直接写为:Compare com com(x,y),这时候肯定会有人说有什么用呢,用其他方式也能替代。如果这样想那就错了,仿函数作为STL的六大接口之一又怎么会没用呢?下面我们就能见识到仿函数的重要性:
void adjust_up(int child)
{
Compare com;
size_t parent = (child - 1) / 2;
while (child > 0)
{
//if (_con[parent] < _con[child])
if (com(_con[parent],_con[child]))
{
swap(_con[parent], _con[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}对于向上调整函数的实现我们先创建一个仿函数对象,然后计算孩子节点的父节点,当孩子节点大于0时进入循环,在这里我们是不用判断child>=0的,因为等于0这个孩子就变成所有节点的祖先了还哪有父节点呢?然后我们直接用仿函数判断如果父亲小于孩子(因为默认是大堆)节点就进行向上调整,向上调整就是将父节点和孩子节点交换,然后让孩子节点到以前父节点的位置上,在重新算父节点这样就能依次向上连续调整,一旦发现父节点大于孩子节点满足大堆的条件我们就break即可。在这里如果没有这个仿函数,我们该如何随意控制优先级队列是大堆还是小堆呢?所以仿函数真的很重要。
void adjust_down(int parent)
{
Compare com;
size_t child = 2 * parent + 1;
while (child < _con.size())
{
//if ((child + 1) < _con.size() && _con[child] < _con[child + 1])
if ((child+1)<_con.size()&&com(_con[child],_con[child+1]))
{
++child;
}
//if (_con[parent] < _con[child])
if (com(_con[parent],_con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}向下调整函数是将父节点依次和左右孩子节点相比较,默认是大堆,如果父节点小于孩子节点就交换,由于向下调整的时候我们需要看孩子节点哪个更大,父节点与大的那个孩子节点交换,所以我们先默认孩子节点是左孩子,由于孩子节点是依次向下调整的,所以循环条件为孩子小于size()就进入循环,进入循环后我们首先判断右孩子是否存在,因为一个完全二叉树是有可能没有右孩子的。如果右孩子存在并且左孩子小于右孩子我们就让孩子节点++变成右孩子。当父节点小于孩子节点的时候我们就进行调整,先交换父节点和孩子节点,然后让父节点到刚刚孩子节点的位置上去,再重新计算孩子节点。当父节点不小于孩子节点时就不需要调整直接break即可。
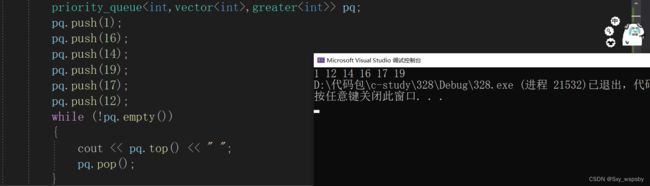
下面我们验证一下我们写的优先级队列:
因为默认是大堆所以我们看到确实排序完成了,下面我们换个适配器验证一下小堆。
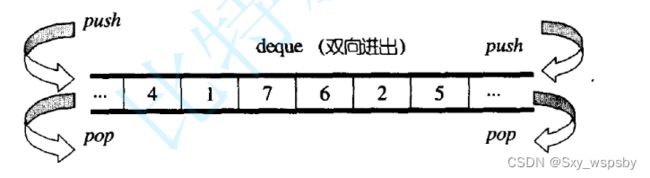
下面我们简单的介绍一下什么是deque:
deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维数组,其底层结构如下图所示:
那deque是如何借助其迭代器维护其假想连续的结构呢?看下图:
我们可以看到deque的实现非常的复杂,虽然插入删除比vector方便了不少并且对于空间的扩容也优于vector,但却没有极致的优点,所以只能沦为容器适配器。
总结
本节相对比较简单,因为很多都是我们之前学过的知识,本篇文章的重点在于了解并且会熟悉的使用适配器,我们会发现有了适配器是非常方便的,之前我们用C语言写栈和队列的时候随便就一两百行代码,而用c++实现栈和队列不到60行就能搞定。deque的出现本来是为了替代vector和list的,结果却成为了stack和queue的容器适配器,这是因为deque没有一个极致的优点,不像vector那样可以随意访问元素,也不能像list那样任意位置插入删除的效率高。下一篇要讲的内容是反向迭代器的实现与适配(干货满满哦~)。