python实现模糊综合评价法(FCE)
1 基本概念
- 综合评价是指按预定的目的确定研究对象的属性 (指标 ) 并将这种属性变为客观定量的计值或主观效用的行为 。
- 评价特指多属性对象的综合评价 。属性是关于目的的框架结构是对研究对象本质特征的概括 。
- 指标是关于研究对象属性的测度是对对象属性的具体化 。
2 模糊综合评价法简介
在客观世界中存在着许多不确定性的现象这种不确定性主要表现在两个方面: 一是随机性二是模糊性 。
- 随机性造成的不确定性是由于对事物的因果律掌握不够,也就是说对事物发生的条件无法严格控制,以致一些偶然因素使实验结果产生了不确定性,但事物本身却是有明确的含义的,随机事件的特点是实验结果的不可预知性 。
- 模糊性是指某些事物或概念的边界不清楚,这种边界不清的模糊概念,不是由于人的主观认识达不到客观实际所造成的,而是事物的一种客观属性,是事物的差异之间存在着中间过渡过程的结果 。例如 关于地震的震级、咫风的强度,对某种质量的评定以及生活中区分青年 、中年和老年等 。由于评定实物的标准或事物本身的定义没有明确的 “ 边界 ” 从而构成不确定性 。
因此对具有模糊性的因素,人为定制标准去评价,其结果包含人的主观意识,是不准确的。
所以,在评价过程中,应用模糊关系合成原理,将边界不清、不易评价的因素定量化,即糊综合评价法(FCE,Fuzzy Comprehension Evaluation Method)。
3 模糊综合评价法思想和原理
FCE是一种根据模糊数学隶属度理论把定性评价转化为定量评价的方法。
模糊数学产生于1965年,美国伯克利加利福尼亚大学的L. A. Zadeh教授发表的《模糊集》, 第一次成功地将模糊概念用精确的数学方法进行了描述,提供了一种分析复杂系统的新方法。
后由北京师范大学的汪培庄先生提出了模糊数学的一种具体应用方法-模糊综合评价法。
模糊综合评价法的基本思想是根据多目标评价问题的性质和总目标,把问题本身按层次进行分解。因此在决策时,大体上可以可分为四个步骤:

模糊综合评价法的基本思想是用隶属与“是”或“不是”的程度代替“是”或 “不是”, 刻画一种“中介状态”。
其基本原理是:
- 首先确定被评价的指标或因素以及评价标准;
- 第二步确定各指标的权重及它们隶属于各评价标准的程度,计算得到模糊综合评价矩阵;
- 最后将 模糊综合评价矩阵与指标的隶属程度向量进行模糊运算,对结果进行归一化处理,得到最终 的综合评价结果。
4 模糊综合评价法的步骤
模糊综合评价法一般包括确定指标集、评价集、单因素评价和综合评价四大部分内容。 其具体计算步骤如下:
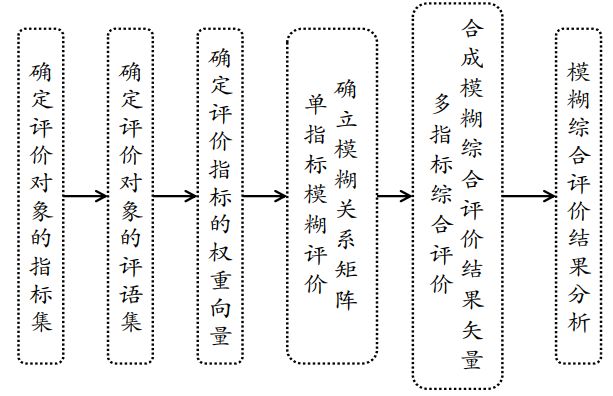
1)确定评价对象的指标集
为了便于权重分配与评价,可以按照评价指标的属性将其分成若干类, 把每一类都视作单一评价指标,并称之为一级评价指标。一级指标可以设置下属的二级指标, 依此类推。
假设以企业组织和管理水平评价为例,用模糊综合评价方法给出定量评价。这是专家(或其他统计方式)对评价打分表投票表决结果统计数据,简单的说就是对需要评价的因素(指标)给出主管或客观的“优、良、一般、较差、非常差”评价。这样,我们能给企业什么样的评价呢?
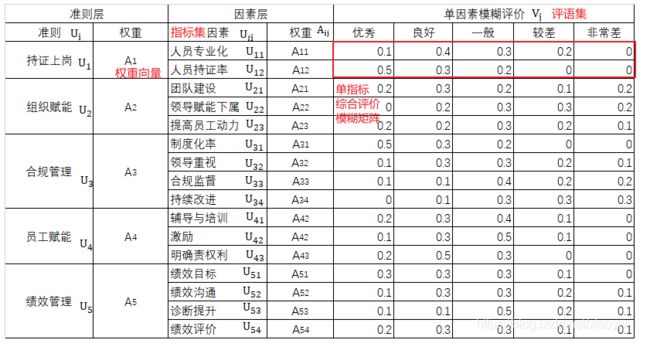
2)确定评价对象评语集
一般划分为3~5个等级。
3)确定评价因素的权重向量
权重是以某种数量形式对比、权衡被评价事物总体中各指标相对重要程度的量值
方法:AHP法、CRITIC法…
AHP法确认的权重:
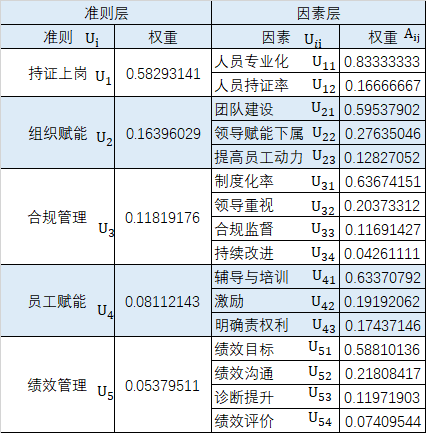
4)进行单指标模糊评价,建立模糊关系矩阵R
首先对一个指标进行评价,计算被评价对象隶属于评价集合V的程度,得到单指标模糊评价结果。
在构造多等级模糊子集后,从每个因素上量化被评价对象,确定被评价对象对各级模糊子集的隶属度,从而获得模糊关系矩阵。
对模糊关系矩阵进行归一化处理,消除量纲的影响。
归一化处理(隶属度函数):

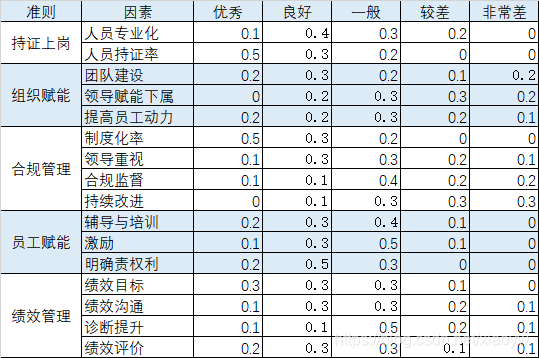
先对评价表中的每个因素隶属于各个评语的程度进行评价(专家打分或隶属度函数)。以部分投票结果为例。
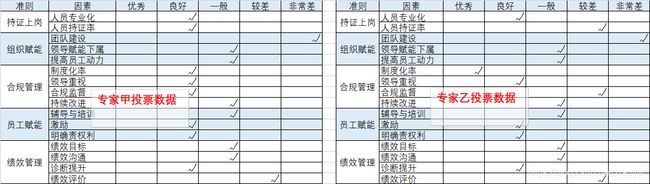
10名专家分别打分,以“持证上岗”准则为例,对“人员专业化”单因素模糊评价,选优秀1人,良好5人,一般3人,较差2人,非常差0人,按频率占比方法则优秀为0.1,如下表所示。
5)多指标综合评价
利用合理的模糊合成算子合成模糊权向量W与模糊关系矩阵R,计算得到各被评价对象的模糊综合评价结果向量B。
模糊合成算子:

共有四种模糊算子:
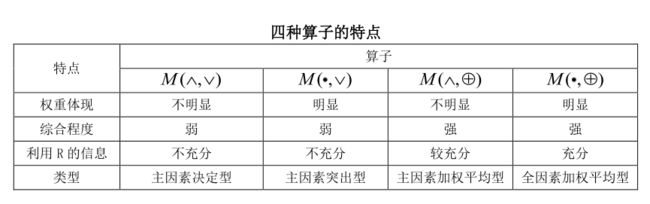
详见:https://blog.csdn.net/qq_42374697/article/details/105883545
在实例中,最后得到的模糊向量为:
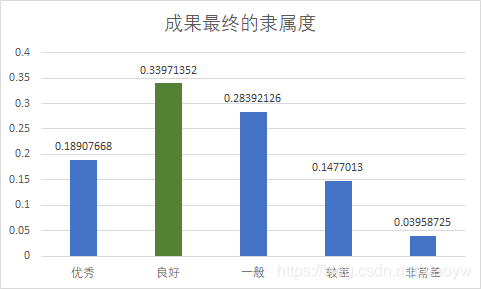
B = A 1 × m ∘ R m × n = ( 0.18907668 , 0.33971352 , 0.28392126 , 0.1477013 , 0.03958725 ) B=A _{1×m}∘R _{m×n} =(0.18907668,0.33971352,0.28392126,0.1477013,0.03958725) B=A1×m∘Rm×n=(0.18907668,0.33971352,0.28392126,0.1477013,0.03958725)
由计算结果可见,该成果应被评为良好。
6)对模糊综合评价结果进行分析
评价结果向量B是被评价对象对各个等级的隶属程度描述。
由于评价结果为一个模糊向量不能直接用于排序择优,还需要对结果进行综合分析,计算每个评价对象的综合分值,按大小进行排序,按序择优,从而挑选出最优者。
主要采用加权平均原则对结果进行处理,最终确定被评价对象的相对得分。
系统总得分:
F = B 1 × n × S 1 × n T F=B_{1×n}×S_{1×n}^{T} F=B1×n×S1×nT
其中 F F F 为系统总得分, S S S 为 V V V 中相应因素的级分。
在实例中,优秀的级分肯定最高,其次是良好,依次往下,设级分依次为 S = ( 1 , 0.8 , 0.6 , 0.4 , 0.2 ) S = ( 1 , 0.8 , 0.6 , 0.4 , 0.2 ) S=(1,0.8,0.6,0.4,0.2),则该成果最后的系统总得分为 69.82 69.82 69.82。
5 Python实现
#模糊综合评价法(FCE),输入准则权重、因素权重
def fuzzy_eval(criteria, eigen):
#量化评语(优秀、 良好、 一般、 较差、 非常差)
score = [1,0.8,0.6,0.4,0.2]
df = get_DataFromExcel()
print('单因素模糊综合评价:{}\n'.format(df))
#把单因素评价数据,拆解到5个准则中
v1 = df.iloc[0:2,:].values
v2 = df.iloc[2:5,:].values
v3 = df.iloc[5:9,:].values
v4 = df.iloc[9:12,:].values
v5 = df.iloc[12:16,:].values
vv = [v1,v2,v3,v4,v5]
val = []
num = len(eigen)
for i in range(num):
v = np.dot(np.array(eigen[i]),vv[i])
print('准则{} , 矩阵积为:{}'.format(i+1,v))
val.append(v)
# 目标层
obj = np.dot(criteria, np.array(val))
print('目标层模糊综合评价:{}\n'.format(obj))
#综合评分
eval = np.dot(np.array(obj),np.array(score).T)
print('综合评价:{}'.format(eval*100))
#获取专家评价数据
def get_DataFromExcel():
df = pd.read_excel('FCE.xlsx')
return df
运行程序,输出结果:
单因素模糊综合评价:
优秀 良好 一般 较差 非常差
0 0.1 0.4 0.3 0.2 0.0
1 0.5 0.3 0.2 0.0 0.0
2 0.2 0.3 0.2 0.1 0.2
3 0.0 0.2 0.3 0.3 0.2
4 0.2 0.2 0.3 0.2 0.1
5 0.5 0.3 0.2 0.0 0.0
6 0.1 0.3 0.3 0.2 0.1
7 0.1 0.1 0.4 0.2 0.2
8 0.0 0.1 0.3 0.3 0.3
9 0.2 0.3 0.4 0.1 0.0
10 0.1 0.3 0.5 0.1 0.0
11 0.2 0.5 0.3 0.0 0.0
12 0.3 0.3 0.3 0.1 0.0
13 0.1 0.3 0.3 0.2 0.1
14 0.1 0.1 0.5 0.2 0.1
15 0.2 0.3 0.3 0.1 0.1
准则1 , 矩阵积为:[0.16666667 0.38333333 0.28333333 0.16666667 0. ]
准则2 , 矩阵积为:[0.14472991 0.2595379 0.2404621 0.16809714 0.18717295]
准则3 , 矩阵积为:[0.35043549 0.26809492 0.24801728 0.07691281 0.0565395 ]
准则4 , 矩阵积为:[0.18080794 0.33487429 0.40175492 0.08256285 0. ]
准则5 , 矩阵积为:[0.22502982 0.27605619 0.32394381 0.13378032 0.04118986]
目标层模糊综合评价:[0.18907668 0.33971352 0.28392126 0.1477013 0.03958725]
综合评价:69.81982179113338
参考:
模糊层次综合评价法及其应用-江高.
基于模糊综合评价的海绵城市LID措施综合效能评价体系研究-马萌华.
https://blog.csdn.net/xiaoyw71/article/details/108404950
https://blog.csdn.net/qq_42374697/article/details/105883545
https://blog.csdn.net/cyj972628089/article/details/107616236