数据结构与算法--字符串匹配算法
目录
概要
单模式与多模式的区别
单模式匹配算法
BF算法
概念
代码实现
时间复杂度
应用
RK算法
概念
代码实现
时间复杂度
应用
BM算法
概念
算法原理
代码实现
时间复杂度
应用
多模式匹配算法
Trie树
概念
Trie树的插入
Trie树的查找
代码实现
时间复杂度
应用
概要
字符串匹配这个功能,是非常常见的功能,比如"Hello"里是否包含"el"? 在 Java 里用的是indexOf函数,其底层就是字符串匹配算法。主要分类如下:
单模式与多模式的区别
单模式匹配算法即在一段文本中匹配单个字符串,多模式匹配算法则是在多个字符串中寻找匹配的字符串。
单模式匹配算法
BF算法
概念
BF即是 Brute Force 缩写,即暴力匹配算法,也称为朴素匹配算法。例如在A字符串中查找B字符串,因此从A字符串的起始位置依次向后匹配,看是否有匹配的字符串。
代码实现
public class Bfalth {
public static boolean isMatch(String main, String sub){
for (int i = 0; i <= (main.length() - sub.length()); i++){
if (main.substring(i, i + sub.length()).equals(sub)){
return true;
}
}
return false;
}
}时间复杂度
m:匹配串的长度 n:为主串的长度
每次需要对比 m 个字符,需要对比 n - m + 1 次,所以最坏情况的时间复杂度为 O(n * m)。
应用
BF算法 效率不高但是实现简单,适用于 主串不是很长的场景。
RK算法
概念
RK算法 全称 Rabin-Karp算法,由发明者 Rabin 和 Karp 名字命名的。
由于 BF算法 每次需要检查主串与子串是否匹配,需要依次对比字符,所以时间复杂度比较高,如果引入哈希算法的话,时间复杂度就会降低很多。因此 RK算法 通过哈希算法对主串中的 n-m+1 个字串分别进行哈希求值,逐个比较hash的大小,如果相等则表示子串与主串匹配了。因为哈希值是数字,数字间比较非常快速,所以查找效率会提高。
代码实现
public class RKalth {
public static boolean isMatch(String main, String sub){
int hash_sub = strToHash(sub);
for (int i = 0; i <= (main.length() - sub.length()); i++){
if (hash_sub == strToHash(main.substring(i, i + sub.length()))){
return true;
}
}
return false;
}
/**
* hash算法可以自己设计
*/
public static int strToHash(String src){
int hash = 0;
for (int i = 0; i < src.length(); i++){
hash *= 26;
hash += src.charAt(i) - 97;
}
return hash;
}
}时间复杂度
m:匹配串的长度 n:为主串的长度
RK算法时间复杂度 O(m + n)
应用
适用于匹配串类型不多的情况,比如:字母、数字或字母加数字的组合 62 (大小写字母+数字)
BM算法
概念
BM(Boyer - Moore)算法是一种非常高效的字符串匹配算法,举例来说:
在这个例子中,主串中的 c,在子串中是不存在的,所以,子串向后滑动的时候,只要 c 与子串有重合,肯定无法匹配。所以,我们可以一次性把子串往后多滑动几位,把子串移动到 c 的后面。
BM算法本质上其实就是在寻找这种规律。借助这种规律,在子串与主串匹配的过程中,当子串和主串某个字符不匹配的时候,能够跳过一些肯定不会匹配的情况,将子串往后多滑动几位。
算法原理
BM算法包含两部分,分别是坏字符规则(bad character rule)和 好后缀规则(good suffix shift)。
- 坏字符规则
BM算法的匹配顺序比较特别,是按照子串下标从大到小的顺序匹配的。
我们从子串的末尾倒着往前匹配,当某个字符没法匹配的时候,我们把这个字符称作坏字符(主串中的字符)。
字符 c 与子串中的任何字符都不可能匹配。这个时候,我们可以将子串直接往后滑动三位,将子串滑动到 c 后面的位置,再从子串的末尾字符开始比较。
坏字符 a 在子串中是存在的,子串中下标是 0 的位置也是字符 a。这种情况下,我们可以将子串往后滑动两位,让两个 a 上下对齐,然后再从子串的末尾字符开始,重新匹配。
当发生不匹配的时候,我们把坏字符对应的子串中的字符下标记作 si。如果坏字符在子串中存在,我们把这个坏字符在子串中的下标记作 xi。如果不存在,我们把 xi 记作 -1。那子串往后移动的位数就等于 si - xi 。(下标,都是字符在模式串的下标)
第一次移动 3 位, c 在模式串中不存在,所以 xi = -1, 移动位数 n = 2 - (-1) = 3
第二次移动 2 位,a 在模式中存在,所以xi = 0, 移动位数 n = 2 - 0 = 2
- 好后缀规则
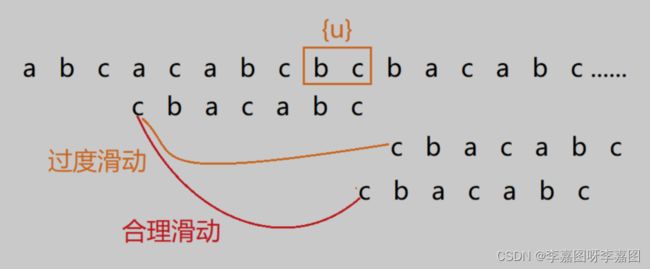
我们把已经匹配的我们拿它在子串中查找,如果找到了另一个跟{u}相匹配的子串{u},那我们就将子串滑动到子串{u}与主串中{u}对齐的位置。
如果在子串中找不到另一个等于{u}的子串,我们就直接将子串,滑动到主串中{u}的后面,因为之前的任何一次往后滑动,都没有匹配主串中{u}的情况。
过度滑动情况:
所以,针对这种情况,我们不仅要看好后缀在子串中,是否有另一个匹配的子串,我们还要考察好后缀的后缀子串(c),是否存在跟模式串的前缀子串(c)匹配的。
如何选择坏字符和好后缀
我们可以分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数。
代码实现
坏字符
如果我们拿坏字符,在模式串中顺序遍历查找,这样就会比较低效
可以采用散列表,我们可以用一个256数组,来记录每个字符在模式串中的位置,数组下标可以直接对应字符的ASCII码值,数组的值为字符在模式串中的位置,没有的记为 -1
bc[97]=a
bc[98]=b
bc[100]=d
有重复的字母以后面的位置为准
public class BMalth {
private static final int SIZE = 256;
private static void generateBC(char[] b, int m, int[] dc){
for (int i = 0; i < SIZE; i++){
dc[i] = -1;
}
for (int i = 0; i < m; ++i){
int ascii = (int)b[i];
dc[ascii] = i;
}
}
public static int bad(char[] a, char[] b){
//主串长度
int n = a.length;
//子串长度
int m = b.length;
//创建字典
int[] bc = new int[SIZE];
//构建坏字符哈希表,记录子串中每个字符最后出现的位置
generateBC(b, m, bc);
//i表示主串与子串对齐的第一个字符
int i = 0;
while (i <= n - m){
int j;
for (j = m - 1; j >= 0; --j){
// 子串从后往前匹配
//i+j: 不匹配的位置
if (a[i + j] != b[j]){
// 坏字符对应模式串中的下标是j
break;
}
}
if (j < 0){
// 匹配成功,返回主串与模式串第一个匹配的字符的位置
return i;
}
// 这里等同于将模式串往后滑动j-bc[(int)a[i+j]]位
// j:si bc[(int)a[i+j]]:xi
i = i + (j - bc[(int)a[i + j]]);
}
return -1;
}
}时间复杂度
m:匹配串的长度 n:为主串的长度
BM算法的时间复杂度是O(N/M)
应用
BM算法比较高效,在实际开发中,特别是一些文本编辑器中,用于实现查找字符串功能。
多模式匹配算法
Trie树
概念
Trie 树,也叫“字典树”。它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
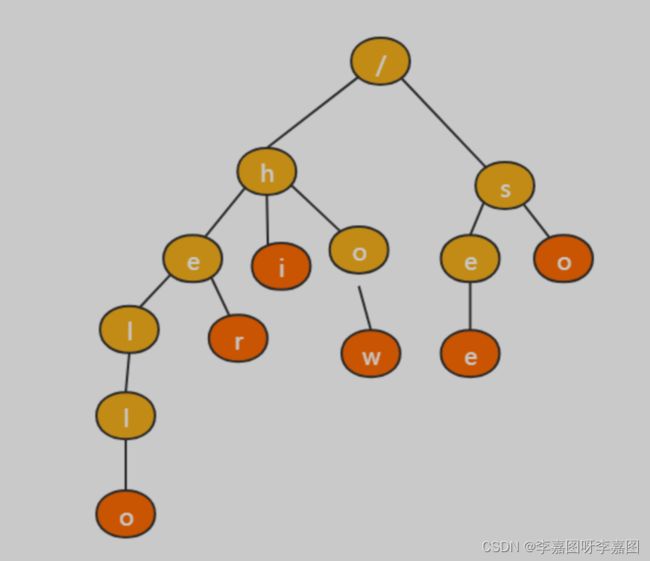
比如:有 6 个字符串,它们分别是:how,hi,her,hello,so,see,我们可以将这六个字符串组成Trie树结构。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
其中,根节点不包含任何信息。每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(红色节点为叶子节点)
Trie树的插入
Trie树的查找
当我们在 Trie 树中查找一个字符串的时候,比如查找字符串“her”,那我们将要查找的字符串分割成单个的字符 h,e,r,然后从 Trie 树的根节点开始匹配。
Trie 树是一个多叉树,我们通过一个下标与字符一一映射的数组,来存储子节点的指针。
假设我们的字符串中只有从 a 到 z 这 26 个小写字母,我们在数组中下标为 0 的位置,存储指向子节点a 的指针,下标为 1 的位置存储指向子节点 b 的指针,以此类推,下标为 25 的位置,存储的是指向的子节点 z 的指针。如果某个字符的子节点不存在,我们就在对应的下标的位置存储 null。
当我们在 Trie 树中查找字符串的时候,我们就可以通过字符的 ASCII 码减去“a”的 ASCII 码,迅速找到匹配的子节点的指针。比如,d 的 ASCII 码减去 a 的 ASCII 码就是 3,那子节点 d 的指针就存储在数组中下标为 3 的位置中。
代码实现
public class TrieNode {
public char data;
public TrieNode[] children = new TrieNode[26];
public boolean isEndingChar = false;
public TrieNode(char data) {
this.data = data;
}
}
public class Trie {
private TrieNode root = new TrieNode('/');
// 往Trie树中插入一个字符串
public void insert(char[] text){
TrieNode p = root;
for (int i = 0; i < text.length; ++i) {
int index = text[i] - 97;
if (p.children[index] == null){
TrieNode newNode = new TrieNode(text[i]);
p.children[index] = newNode;
}
p = p.children[index];
}
p.isEndingChar = true;
}
public boolean find(char[] pattern){
TrieNode p = root;
for (int i = 0; i < pattern.length; ++i) {
int index = pattern[i] - 97;
if (p.children[index] == null){
return false;
}
p = p.children[index];
}
return p.isEndingChar == false ? false : true;
}
}时间复杂度
如果要在一组字符串中,频繁地查询某些字符串,用 Trie 树会非常高效。构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)(n 表示所有字符串的长度和)。但是一旦构建成功之后,后续的查询操作会非常高效。每次查询时,如果要查询的字符串长度是 k,那我们只需要比对大约 k 个节点,就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说,构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k),k 表示要查找的字符串的长度。
应用
利用 Trie 树,实现搜索关键词的提示功能。
假设关键词库由用户的热门搜索关键词组成。我们将这个词库构建成一个 Trie 树。当用户输入其中某个单词时,把这个词作为一个前缀子串在 Trie 树中匹配。假设词库里只有hello、her、hi、how、so、see 这 6 个关键词。当用户输入了字母 h 的时候,我们就把以 h 为前缀的hello、her、hi、how 展示在搜索提示框内。当用户继续键入字母 e 的时候,我们就以 he 为前缀的hello、her 展示在搜索提示框内,这就是搜索关键词提示的最基本的算法原理。