数据结构与算法题目集（中文）编程题

---

7-1 最大子列和问题

const和static的用法没搞清楚！！！

#include 
//#include 
//#include 
using namespace std;

int maxSubSequence(int A[], int N)
{
    int ThisSum,MaxSum,j;
    ThisSum = MaxSum =0;

    for(j = 0; j < N; j++)
    {
        ThisSum += A[j];

        if(ThisSum > MaxSum)
            MaxSum = ThisSum;
        else if(ThisSum < 0)
            //将前面已求和的数列看作一个数，大于0就留下
            //小于0的时候就舍弃前面序列重新开始
            //满足题目小于0当作0.
            ThisSum = 0;
    }
    return MaxSum;
}

int main()
{
    int number = 0;
    scanf("%d", &number);
    int sequence[100001];
    for(int i=0; i<number; i++)
    {
        scanf("%d", &sequence[i]);
    }
    printf("%d", maxSubSequence(sequence, number));
    return 0;
}

7-2 一元多项式的乘法与加法运算

在用结构体数组和链表间考虑了一下，配套慕课是用的链表，那就也试试链表，写完看看比数组方便在哪里。

按理来说传入函数后，是个新的作用域了，不传出去，值是不会改变的。改变传入指针的值！！！？

#include 
using namespace std;

typedef struct PolyNode *Poly;
struct PolyNode{
    int coefficient; //系数
    int exponent; //指数
    Poly next;
};

void create(int c, int e, Poly *tail)
{
    Poly newNode = new PolyNode;
    newNode->coefficient = c;
    newNode->exponent = e;
    newNode->next = NULL;
    //改变传入指针的值！！！
    //头结点是空结点
    (*tail)->next = newNode;
    *tail = newNode;
}

Poly read()
{
    Poly head, tail; //头尾指针
    head = new PolyNode;
    head->next = NULL;
    tail = head;
    int c, e, n;
    scanf("%d", &n);
    while(n--)
    {
        scanf("%d %d", &c, &e);
        create(c, e, &tail); //传入引用还是地址来着？!!!
    }
    return head->next;
}

void printp(Poly head)
{
    Poly p = head;
    if(!p)
    {
        printf("0 0\n");
        return;
    }
    while(p->next)
    {
        printf("%d %d ", p->coefficient, p->exponent);
        p = p->next;
    }
    printf("%d %d\n", p->coefficient, p->exponent);
}

Poly add(Poly p1, Poly p2)
{
    Poly addHead, tail;
    addHead = new PolyNode;
    addHead->next = NULL;
    tail = addHead;
    int tmp = 0;
    while(p1&&p2)
    {
        if(p1->exponent == p2->exponent)
        {
            tmp = p1->coefficient + p2->coefficient;
            if(tmp != 0)
            {
                //这个容易忘记哎
                create(tmp, p1->exponent, &tail);
            }
            p1 = p1->next;
            p2 = p2->next;
        }
        else if(p1->exponent > p2->exponent)
        {
            create(p1->coefficient, p1->exponent, &tail);
            p1 = p1->next;
        }
        else
        {
            create(p2->coefficient, p2->exponent, &tail);
            p2 = p2->next;
        }
    }
    while(p1)
    {
        create(p1->coefficient, p1->exponent, &tail);
        p1 = p1->next;
    }
    while(p2)
    {
         create(p2->coefficient, p2->exponent, &tail);
         p2 = p2->next;
    }
    return addHead->next;
}

Poly mul(Poly p1, Poly p2)
{
    Poly mulHead, tail, tmp;
    tmp = new PolyNode;
    tmp->next = NULL;
    tail = tmp;
    mulHead = NULL;
    int c, e;

//    printf("____________________________\n");
//    printf("p1: ");
//    printp(p1);
//    printf("p2: ");
//    printp(p2);

    if(!p1 || !p2)
    {
        return NULL;
    }
    while(p1)
    {
        Poly t2 = p2;
        while(t2)
        {
            c = p1->coefficient * t2->coefficient;
            e = p1->exponent + t2->exponent;
            create(c, e, &tail);
            t2 = t2->next;
        }
        tmp = tmp->next;

//        printf("tmp: ");
//        printp(tmp);
//        printf("__________________________\n");
        mulHead = add(tmp, mulHead);
        //新的乘积
        tmp->next = NULL;
        tail = tmp;
        p1 = p1->next;
    }
    return mulHead;
}

int main()
{
    Poly p1, p2, pAdd, pMul;
    p1 = read();
    p2 = read();
//    printf("pAdd: ");
//    printf("__________________________\n");
    pMul = mul(p1, p2);
    printp(pMul);
    pAdd = add(p1, p2);
    printp(pAdd);
}

感觉用两种结构体都差不多，因为每次加法和乘法都是开辟新的空间。

7-3 树的同构

完全没思路，连这棵树是怎么读取去构成都不知道。老师讲解视频

两棵树如果是同构的，他们对应节点的儿子是一样的，左右位置可以不同。
解题关键：
1、二叉树表示
一般用链表表示，或者看作完全二叉树用数组表示。这里用一种新的结构去表示。

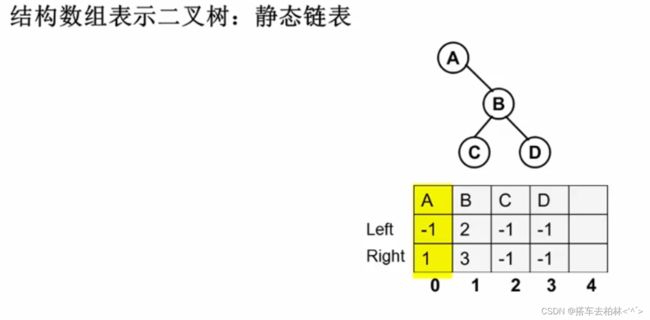
2、建二叉树
可以发现Left和Right都是存的左右孩子结点，那么根结点就是没有被存储的那个结点啦，泪目。用.和->去指向结构体某个属性到底是啥区别呢？！ 而且为啥输入会不能读取呢？cpp的cin>>用法又是什么

3、同构判别
先写出递归出口，然后分情况讨论递归。

#include 
using namespace std;

#define ElementType char
#define MaxTree 11
#define Tree int
#define null -1

struct TreeNode
{
    ElementType Element;
    Tree Left;
    Tree Right;
} T1[MaxTree], T2[MaxTree];
//用结构体数组表示二叉树

Tree buildTree(struct TreeNode T[])
{
    int n = 0;
    Tree root = null;
    ElementType left, right;

    scanf("%d", &n);
    if(n)
    {
        int check[n];
        for(int i=0; i<n; i++)
        {
            check[i] = 0;
        }

        for(int i=0; i<n; i++)
        {
            //scanf("%c %c %c\n", &T[i].Element, &left, &right);
            //这样输入的问题是&T.Element根本不会装变量
            //scanf("\n%c %c %c", &T[i].data, &a, &b); //网友的方法
            cin >> T[i].Element >> left >> right;
            if(left == '-')
                T[i].Left = null;
            else
            {
                T[i].Left = left-'0'; //数字字符转为数字的方法
                check[T[i].Left] = 1;
            }
            if(right == '-')
                T[i].Right = null;
            else
            {
                T[i].Right = right-'0';
                check[T[i].Right] = 1;
            }
        }

        for(int i=0; i<n; i++)
        {
            if(!check[i])
            {
                root = i;
                break;
            }
        }
    }
    return root;
}

int isOmorphic(Tree R1, Tree R2)
{
    //分情况递归下去是我没想到的，泪目

    //递归出口
    //根节点为空
    if(R1==null && R2==null)
    {
        return 1;
    }
    //根结点一空一不空
    if(R1*R2<0)
    {
        return 0;
    }
    //根节点值不一样
    if(T1[R1].Element != T2[R2].Element)
    {
        return 0;
    }

    //还不能结束判断
    //如果左子树都空，那么递归判别右子树
    if(T1[R1].Left==null && T2[R2].Left==null)
    {
        return isOmorphic(T1[R1].Right, T2[R2].Right);
    }
    //左边都不空，要判断是不是交换过一次了！！！那对比的左右结点是不同的
    if((T1[R1].Left!=null && T2[R2].Left!=null)&&(T1[T1[R1].Left].Element == T2[T2[R2].Left].Element))
    {
        return ((isOmorphic(T1[R1].Right, T2[R2].Right)) && (isOmorphic(T1[R1].Left, T2[R2].Left)));
    }
    else
    {
         return ((isOmorphic(T1[R1].Right, T2[R2].Left)) && (isOmorphic(T1[R1].Left, T2[R2].Right)));
    }
}

int main()
{
    Tree R1, R2;

    R1 = buildTree(T1);
    R2 = buildTree(T2);

    if(isOmorphic(R1,R2))
        printf("Yes\n");
    else
        printf("No\n");

    return 0;
}

7-4 是否同一棵二叉搜索树

按理来说 有不用把所有树都构造出来的方法。 之后找视频看看吧。

#include 
using namespace std;

typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode
{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

void InorderTraversal( BinTree BT )
{//中序
    if(!BT)
    {
        return;
    }
    InorderTraversal( BT->Left );
    printf(" %d",BT->Data);
    InorderTraversal( BT->Right );
}


BinTree Insert( BinTree BST, ElementType X )
{
    BinTree node = (BinTree)malloc(sizeof(struct TNode));
    node->Data = X;
    node->Left = NULL;
    node->Right = NULL;
    if(!BST)
    {
        return node;
    }
    BinTree p = BST;
    while(1)
    {
        if(p->Data > X)
        {
            if(!p->Left)
            {
                p->Left = node;
                return BST;
            }
            p = p->Left;
        }
        else if(p->Data < X)
        {
            if(!p->Right)
            {
                p->Right = node;
                return BST;
            }
            p = p->Right;
        }
    }
}

void Justify( BinTree BT1, BinTree BT2 )
{
    if(!BT1 && !BT2)
    {
        printf("Yes\n");
        return;
    }
    if((!BT1&&BT2) || (BT1&&!BT2))
    {
        printf("No\n");
        return;
    }


    BinTree queen[22];
    BinTree temp1, temp2;
    int front=0, rear=0;
    if(BT1->Data == BT2->Data)
    {
        queen[rear++] = BT1;
        queen[rear++] = BT2;
    }
    else
    {
        printf("No\n");
        return;
    }

    while(front != rear)
    {
        temp1 = queen[front++];
        temp2 = queen[front++];

        if(!temp1->Left && !temp2->Left){}
        else if(temp1->Left->Data == temp2->Left->Data)
        {
            //printf("1: %d\n", temp1->Left->Data);
            //printf("2: %d\n", temp2->Left->Data);
            queen[rear++] = temp1->Left;
            queen[rear++] = temp2->Left;
        }
        else
        {
            printf("No\n");
            return;
        }
        if(!temp1->Right && !temp2->Right){}
        else if(temp1->Right->Data == temp2->Right->Data)
        {
            //printf("1r: %d\n", temp1->Right->Data);
            //printf("2r: %d\n", temp2->Right->Data);
            queen[rear++] = temp1->Right;
            queen[rear++] = temp2->Right;
        }
        else
        {
            printf("No\n");
            return;
        }
    }
    printf("Yes\n");
    return;
}


int main()
{
    BinTree BST, Tmp;
    ElementType X;
    int N, times, i;


    while(1)
    {
        scanf("%d", &N);
        if(!N)
        {
            break;
        }
        scanf("%d",&times);

        //读入标准查找树
        BST = NULL;
        for ( i=0; i<N; i++ )
        {
            scanf("%d", &X);
            BST = Insert(BST, X);
        }
        //printf("\n");
        //InorderTraversal(BST);
        //printf("\n");

        while(times--)
        {
            Tmp = NULL;
            for ( i=0; i<N; i++ )
            {
                scanf("%d", &X);
                Tmp = Insert(Tmp, X);
            }
            //printf("\n");
            //InorderTraversal(Tmp);
            //printf("\n");

            Justify(BST, Tmp);
        }

    }
    return 0;
}

7-5 堆中的路径

堆是按照完全二叉树的结构存储的，图解建立最大堆

#include 
using namespace std;


void Swap(int *arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

/*
如果i=0，结点i是根结点，没有双亲结点；否则结点i的双亲结点为(i-1)/2。
如果2* i+1<=n-1,则结点i的左孩子为2*i+1，否则结点i无左孩子。
如果2* i+2<=n-1,则结点i的右孩子为2*i+2,否则结点i无右孩子。
*/

int* BuildMinHeap(int N) {
    int *arr = (int*)malloc(N*sizeof(int));
    int f=0, i=0;
    for(int j=0; j<N; j++)
    {
        i = j;
        scanf("%d", &arr[i]);
        f = (i-1)/2;
        while(f>=0 && arr[i] < arr[f])
        {
            Swap(arr, i, f);
            i = f;
            f = (i-1)/2;
            if(i <= 0)
            {
                break;
            }
        }
    }
    return arr;
}


int main()
{
    int N, M;
    scanf("%d %d", &N, &M);
    if(N)
    {
        int* h = BuildMinHeap(N);
        int index = 0;
        while(M--)
        {
           scanf("%d", &index);
           --index;
           while(index)
           {
               printf("%d ", h[index]);
               index = (index-1)/2;
           }
           printf("%d\n", h[0]);
        }
    }
    return 0;
}

7-6 列出连通集

#include 
#include 
#include 

#define Max 11

using namespace std;

int N, E;
int Map[Max][Max];
int flag[Max];

void DFS(int beg)
{
    flag[beg] = 1;
    printf(" %d", beg);
    for(int i=0; i<N; i++)
    {
        if(Map[beg][i]==1 && flag[i]==0)
        {
            DFS(i);
        }
    }
}

void BFS(int beg)
{
    flag[beg] = 1;
    queue<int> q;
    q.push(beg);
    int temp;
    while(!q.empty())
    {
        temp = q.front();
        printf(" %d", temp);
        q.pop();
        for(int i=0; i<N; i++)
        {
            if(Map[temp][i]==1 && flag[i]==0)
            {
               flag[i] = 1;
               q.push(i);
            }
        }
    }

}

int main()
{
    scanf("%d %d", &N, &E);
    memset(Map, 0, sizeof(Map));
    memset(flag, 0, sizeof(flag));
    int x, y;
    while(E--)
    {
        scanf("%d %d", &x, &y);
        Map[x][y] = 1;
        Map[y][x] = 1;
    }

    for(int i=0; i<N; i++)
    {
        if(!flag[i])
        {
            printf("{");
            DFS(i);
            printf(" }\n");
        }
    }

    memset(flag, 0, sizeof(flag));

    for(int i=0; i<N; i++)
    {
        if(!flag[i])
        {
            printf("{");
            BFS(i);
            printf(" }\n");
        }
    }

    return 0;
}

7-7 六度空间

因为结点很多，所以用链表去存储，矩阵存储的话稀疏就很浪费空间和遍历的时间。然后用BFS去入栈连同他自己这个结点，一共入栈7次。但是还是用矩阵写的快，而且难点是判断第几层

有一个原因造成部分错误，就是0.2f是四舍五入，如果写截断反而会报错 printf("%d: %0.2f%%\n", i, ((int)(percentage*100))/100.0);。

算百分比不能double = int/int，int/int得到的就是int，只不过变成double单纯加了个小数点再赋值的。这也是容易错误的地方。

#include 
#include 
#include 
#include 

#define Max 1001

using namespace std;

int N, E;
int Map[Max][Max];
int flag[Max];

int BFS(int beg)
{
    flag[beg] = 1;
    int times = 0;
    int sum = 1;
    queue<int> q;

    q.push(beg);
    int temp, last = beg, tail = -1;

    while(!q.empty())
    {
        temp = q.front();
        for(int i=1; i<=N; i++)
        {
            if(Map[temp][i]==1 && flag[i]==0)
            {
               flag[i] = 1;
               tail = i;
               q.push(i);
               sum++;
               //printf("%d--", i);
            }
        }

        q.pop();
        if(last == temp)
        {
            times++;//记住每层入队的最后一个，他出队的时候，就是一层了
            last = tail;
            //printf("\n");
        }
        if(times == 6)
        {
            break;
        }
    }
    return sum;
}

int main()
{
    scanf("%d %d", &N, &E);
    memset(Map, 0, sizeof(Map));
    memset(flag, 0, sizeof(flag));
    int x, y;
    while(E--)
    {
        scanf("%d %d", &x, &y);
        Map[x][y] = 1;
        Map[y][x] = 1;
    }

    double percentage;
    for(int i=1; i<=N; i++)
    {
        percentage = (double)BFS(i)*100/(double)N;
        printf("%d: %0.2f%%\n", i, percentage);
        memset(flag, 0, sizeof(flag));
    }

    return 0;
}

7-8 哈利·波特的考试

无向图的多元最短路径算法；如果图不连通，就直接输出0.小白专场
弗洛伊德算法模板：

bool Floyd_Standard(MGraph Graph, WeightType D[][Max], Vertex path[][Max])
{
    Vertex i, j, k;
    //初始化
    for(i=0; i<Graph->Nv; i++)
    {
        for(j=0; j<Graph->Nv; j++)
        {
            D[i][j] = Graph->G[i][j];
            path[i][j] = -1;
        }
    }
    
    for(k=0; k<Graph->Nv; k++)
    {
        for(i=0; i<Graph->Nv; i++)
        {
            for(j=0; j<Graph->Nv; j++)
            {
                if(D[i][k]+D[k][j] < D[i][j])
                {
                    D[i][j] = D[i][k] + D[k][j];
                    if(i==j && D[i][j]<0) //负值圈要不得
                    {
                        return false; 
                    }
                    path[i][j] = k;
                }
            }
        }
    }
    return true;
}

学习数据结构的定义，也正是因为这些数据结构代码很长。Floyed到底怎么回事？！！

#include 

using namespace std;

#define Max 101
#define INFINITY 65535 /*双字节无符号整数最大值*/
typedef int Vertex;
typedef int WeightType;

//定义边
typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1, V2; //顶点
    WeightType Weight;
};
typedef PtrToENode Edge;

//图结点定义
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv; //顶点数
    int Ne; //边数
    WeightType G[Max][Max]; //邻接矩阵
};
typedef PtrToGNode MGraph;

MGraph CreateGraph(int VertexNum)
{
    Vertex V, W;
    MGraph Graph = new GNode;
    Graph->Ne = 0;
    Graph->Nv = VertexNum;
    for(V=0; V<Graph->Nv; V++)
    {
        for(W=0; W<Graph->Nv; W++)
        {
            Graph->G[V][W] = INFINITY;
        }
    }
    return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
    Graph->G[E->V1][E->V2] = E->Weight;
    Graph->G[E->V2][E->V1] = E->Weight;
}

MGraph BuildGraph()
{
    int Nv, i;
    scanf("%d", &Nv);
    MGraph Graph = CreateGraph(Nv);

    scanf("%d", &(Graph->Ne));
    if(Graph->Ne != 0)
    {
        Edge E = new ENode;
        for(i=0; i<Graph->Ne; i++)
        {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
            E->V1--;
            E->V2--;
            InsertEdge(Graph, E);
        }
    }
    return Graph;
}

void Floyd(MGraph Graph, WeightType D[][Max])
{
    Vertex i, j, k;
    //初始化
    for(i=0; i<Graph->Nv; i++)
    {
        for(j=0; j<Graph->Nv; j++)
        {
            D[i][j] = Graph->G[i][j];
        }
    }

    for(k=0; k<Graph->Nv; k++)
    {
        for(i=0; i<Graph->Nv; i++)
        {
            for(j=0; j<Graph->Nv; j++)
            {
                if(D[i][k]+D[k][j] < D[i][j])
                {
                    D[i][j] = D[i][k] + D[k][j];
                }
            }
        }
    }
}

WeightType FindMaxDist(WeightType D[][Max], Vertex i, int N)
{
    WeightType MaxDist;
    Vertex j;
    MaxDist = 0;
    for(j=0; j<N; j++)
    {
        if(j!=i && D[i][j]>MaxDist)
        {
            MaxDist = D[i][j];
        }
    }
    return MaxDist;
}

void FindAnimal(MGraph Graph)
{
    int D[Max][Max];
    int Animal, i, MaxDist;
    Floyd(Graph, D);
    int MinDist = INFINITY;
    for(i=0; i<Graph->Nv; i++)
    {
        MaxDist = FindMaxDist(D, i, Graph->Nv);
        if(MaxDist == INFINITY)
        {
            printf("0\n");
            return;
        }
        if(MinDist > MaxDist)
        {
            MinDist = MaxDist;
            Animal = i+1;
        }
    }
    printf("%d %d\n", Animal, MinDist);
}


int main()
{
    MGraph G = BuildGraph();
    FindAnimal(G);
    return 0;
}

7-9 旅游规划

单源最短路径咯，那就迪杰斯特拉算法？但是为啥会保留两条最短的路径？，那么贪心的时候就还要考虑价格少。其实用弗洛伊德也能算，修改的也不多，但是先练习一下迪杰斯特拉算法。

#include 

using namespace std;

#define Max 501
#define INFINITY 65535 /*双字节无符号整数最大值*/
typedef int Vertex;
typedef int WeightType;

//定义权重结构体
typedef struct WNode *PtrToWNode;
struct WNode
{
    WeightType length; //长度
    WeightType cost; //金额
};
typedef PtrToWNode Weight;

//定义边
typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1, V2; //顶点
    Weight W;
};
typedef PtrToENode Edge;

//图结点定义
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv; //顶点数
    int Ne; //边数
    int departure; //出发地
    int destination; //目的地
    WNode G[Max][Max]; //邻接矩阵
};
typedef PtrToGNode MGraph;

MGraph CreateGraph(int VertexNum)
{
    Vertex V, W;
    MGraph Graph = new GNode;
    Graph->Ne = 0;
    Graph->Nv = VertexNum;
    Graph->departure = -1; //出发地
    Graph->destination = -1; //目的地
    for(V=0; V<Graph->Nv; V++)
    {
        for(W=0; W<Graph->Nv; W++)
        {
            Graph->G[V][W].cost = INFINITY;
            Graph->G[V][W].length = INFINITY;
        }
    }
    return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
    Graph->G[E->V1][E->V2].cost = E->W->cost;
    Graph->G[E->V2][E->V1].cost = E->W->cost;
    Graph->G[E->V1][E->V2].length= E->W->length;
    Graph->G[E->V2][E->V1].length = E->W->length;

}

MGraph BuildGraph()
{
    int Nv, i;
    scanf("%d", &Nv);
    MGraph Graph = CreateGraph(Nv);

    scanf("%d %d %d", &(Graph->Ne), &(Graph->departure), &(Graph->destination));

    if(Graph->Ne != 0)
    {
        Weight W = new WNode;
        Edge E = new ENode;
        E->W = W;
        for(i=0; i<Graph->Ne; i++)
        {
            scanf("%d %d %d %d", &E->V1, &E->V2, &E->W->length, &E->W->cost);
            InsertEdge(Graph, E);
        }
    }
    return Graph;
}

void dijkstra(MGraph p){
    int vis[p->Nv], dis[p->Nv], pay[p->Nv];
    for(int i=0; i<p->Nv; i++)
    {
        vis[i] = 0;
        dis[i] = INFINITY;
        pay[i] = INFINITY;
    }
    int beg = p->departure;
    dis[beg] = 0;
    pay[beg] = 0;


    for(int i=0; i<p->Nv; i++)
    {
        int minDis = INFINITY;
        int minCost = INFINITY;
        int u;
        for(int j=0; j<p->Nv; j++)
        { /*找没被遍历过的距离最小的一个，去贪心*/
            if(!vis[j] && dis[j]<minDis)
            {
                minDis = dis[j];
                u = j;
                minCost = pay[j];
            }
        }
        vis[u] = 1;
        //printf("-------------------------------");
        //printf("当前出发点%d\n", u);

        /* 更新这个正在贪心点的邻接点的到达距离和花费 */
        for(int j=0; j<p->Nv; j++)
        {
            int next;
            while(p->G[u][j].length == INFINITY)
            { //找到一个可达邻接点
                j++;
            }
            next = j;
            //printf("遍历结点：%d\n", j);
            if(!vis[next] && minDis+p->G[u][j].length < dis[next])
            {
                dis[next] = minDis + p->G[u][j].length;
                //printf("距离%d", dis[next]);
                pay[next] = minCost + p->G[u][j].cost;
                //printf("价格%d\n", pay[next]);
            }
            else if(!vis[next] && minDis+p->G[u][j].length==dis[next])
            { //因为不需要记录路径，所以直接更新花费
                if(minCost+p->G[u][j].cost < pay[next])
                {
                    pay[next] = minCost+p->G[u][j].cost;
                    //printf("价格%d\n", pay[next]);
                }
            }
        }
    }
    printf("%d %d", dis[p->destination], pay[p->destination]);
}


int main()
{
    MGraph G = BuildGraph();
    dijkstra(G);
    return 0;
}

我只能说核心代码要反复看，跟着思路走，不然很容易忘！

7-10 公路村村通

这是一个最小生成树问题，特点是：1、无回路；2、n个顶点就有n-1条边；3、包含全部图里的点；4、生成树的所有边都在图里的；5、边的权重和最小。

最小生成树存在<-------->连通图

贪心算法，每次都找权重最小的边，但是约束有：1.只能用图中有的边；2.只能正好用掉顶点数减一条边；3.不能有回路。

Prim算法与Dijkstra算法具有相似的地方。稠密图更加划算。这篇讲的真不错，特别是后面那张图

这个要多复习呀，不然就忘啦

#include 
#include 

using namespace std;

#define Max 1001
#define INFINITY 65535 /*双字节无符号整数最大值*/
typedef int Vertex;
typedef int WeightType;

//定义边
typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1, V2; //顶点
    WeightType pay; //花费
};
typedef PtrToENode Edge;

//图结点定义
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv; //顶点数
    int Ne; //边数
    WeightType G[Max][Max]; //邻接矩阵
};
typedef PtrToGNode MGraph;

MGraph CreateGraph(int VertexNum)
{
    Vertex V, W;
    MGraph Graph = new GNode;
    Graph->Ne = 0;
    Graph->Nv = VertexNum;
    for(V=0; V<Graph->Nv; V++)
    {
        for(W=0; W<Graph->Nv; W++)
        {
            Graph->G[V][W] = INFINITY;
        }
    }
    return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
    Graph->G[E->V1][E->V2] = E->pay;
    Graph->G[E->V2][E->V1] = E->pay;
}

MGraph BuildGraph()
{
    int Nv, i;
    scanf("%d", &Nv);
    MGraph Graph = CreateGraph(Nv);

    scanf("%d", &(Graph->Ne));
    if(Graph->Ne != 0)
    {
        Edge E = new ENode;
        for(i=0; i<Graph->Ne; i++)
        {
            scanf("%d %d %d", &E->V1, &E->V2, &E->pay);
            E->V1--;
            E->V2--;
            InsertEdge(Graph, E);
        }
    }
    return Graph;
}

void prim(MGraph p)
{
    int i, j;
    int minNode;    //记录新纳入的点
    int minPay;    //记录新纳入的点到其余已纳入的点的最小权值
    int sum = 0;    //最小生成树权值和
    int dis[p->Nv], flag[p->Nv]; //记录纳入点权重，是否纳入该点到树中

    memset(dis, INFINITY, sizeof(dis));  //初始化dis数组为无穷大
    memset(flag, 0, sizeof(flag));  //初始化flag数组，0表示此点未被纳入

    /*这里随机选取了0号点为初始时被纳入的顶点*/
    for(i=0; i <= p->Nv; i++)
        dis[i] = p->G[0][i];     //与1号点与其他点的权值存入dis数组
    dis[0] = 0;         //一号点到其本身的权值为0
    flag[0] = 1;        //标记为已纳入


    for(i = 1; i < p->Nv; i++)
    {   //除去初始时随机纳入的点还有n-1个点应被纳入
        minNode = minPay = INFINITY;

        //寻找其邻接的没纳入的权值最小的点
        for(j=0; j<p->Nv; j++)
        {
            if(flag[j] == 0)
            {
                if(dis[j] < minPay)
                {
                    minNode = j;
                    minPay = dis[j];
                }
            }
        }

        if(minNode == INFINITY) //该的点邻接的点已全被纳入
            break;

        sum += minPay;     //将找到的点纳入并标记
        flag[minNode] = 1;


        for(j = 1; j <= p->Nv; j++){
            //我加入了新的点，那么我要把新的点他到其他点的最短距离更新
            if(flag[j] == 0)
                if(dis[j] > p->G[minNode][j])//新的加入点到没被更新的点的距离！！！能避免回路
                    dis[j] = p->G[minNode][j];
        }

    }


    if(i == p->Nv)      //若i等于n则证明已经建立最小生成树
        printf("%d\n", sum);
    else
        printf("-1");
}


int main()
{
    MGraph G = BuildGraph();
    prim(G);
    return 0;
}

当顶点和边同一数量级可以用Kruskal算法贪心。直接从最小权重的边在不构成回路情况下贪心每个边，最后由森林组成树。

7-11 关键活动

7-12 排序

三种语言写的快排模板

7-11 关键活动

没通过的案例和这位同学一样
懒猫老师数据结构

#include 
#include 

using namespace std;


/**
* 算法本身难理解
* 数据结构采用邻接表
* 为了判断图是不是有向无环图，拓扑排序
* 有环的图是不能构成路径的
* 关键路径：带权有向无环图
**/

const int MAX_VERTEX = 101;

//边表
struct ArcNode
{
    int adjvex; //弧终点
    int weight; //权重
    ArcNode *next;
};

//顶点表
struct VertexNode
{
    int vertex; //图的结点信息·
    int in; //图的入度，用于拓扑排序
    ArcNode *firstEdge;
};

/**
* 关键活动有关量：
* 事件最早发生时间ve[k]
* 事件最迟发生时间vl[k]
* 活动最早开始时间ee[i]
* 活动最晚开始时间ev[i]
* 各个活动时间余量el[k]-ee[k],=0即是关键活动
**/

class ALGraph
{
private :
    VertexNode *adjList; //邻接表
    int vertexNum, arcNum;
    int *ve, *vl;
public:
    ALGraph(int v[], int n, int e); //构造函数
    ~ALGraph(); //销毁
    void inputEdges();
    bool setEdge(int vi, int vj, int weight);
    void  displayData();

    bool TopologicalSort(int result[], int &count);
    bool GriticalPath();
};

ALGraph::ALGraph(int v[], int n, int e)
{
    vertexNum = n;
    arcNum = e;
    adjList = new VertexNode[vertexNum];
    for(int i=0; i<vertexNum; i++)
    {
        adjList[i].in = 0;
        adjList[i].vertex = v[i];
        adjList[i].firstEdge = NULL;
    }
    ve = new int[vertexNum];
    vl = new int[vertexNum];
}

bool ALGraph::setEdge(int vi, int vj, int weight)
{
    ArcNode *s;
    if(vi>=0 && vi<vertexNum && vj>=0 && vj<vertexNum && vi!=vj)
    {
        s = new ArcNode;
        s->adjvex = vj;
        s->weight = weight;
        //头插法
        s->next = adjList[vi].firstEdge;
        adjList[vi].firstEdge = s;
        adjList[vj].in++; //入度
        return true;
    }
    else
    {
        //printf("----%d %d %d----", vi, vj, vertexNum);
        return false;
    }
}

void ALGraph ::inputEdges()
{
    for(int i=0; i<arcNum; i++)
    {
        int vi, vj, weight;
        cin >> vi >> vj >> weight;
        if(!setEdge(vi-1, vj-1, weight)) //因为是从0开始存储，并且计数
        {
            //cout << "输入越界" <
            i--;
        }
    }
}

ALGraph::~ALGraph()
{
    ArcNode *p, *pre;
    for(int i=0; i<vertexNum; i++)
    {
        p = adjList[i].firstEdge;
        adjList[i].firstEdge = NULL;
        while(p)
        {
            pre = p;
            p = p->next;
            delete pre;
        }
    }
    delete [] adjList;
    delete [] ve;
    delete [] vl;
}

bool ALGraph::TopologicalSort(int result[], int &count)
{
    int stack[MAX_VERTEX]; //把顶点对应下标压入栈
    int top = -1;
    int inVex;
    int outVex;
    ArcNode *p;

    for(int i=0; i<vertexNum; i++)
    {
        ve[i] = 0; //最早发生时间初始化为0
    }

    //遍历顶点表，把入度为0的压入堆栈
    for(int i=0; i<vertexNum; i++)
    {
        if(adjList[i].in == 0)
        {
            stack[++top] = i;
        }
    }

    count = 0; //处理过的顶点
    while(top != -1)
    {
        inVex = stack[top--];
        result[count] = inVex; //拓扑排序的序列
        count++;

        p = adjList[inVex].firstEdge;
        while(p)
        {
            outVex = p->adjvex;
            adjList[outVex].in--;
            if(adjList[outVex].in == 0)
            {
                stack[++top] = outVex;
            }
            if(ve[inVex]+p->weight > ve[outVex])
            {
                ve[outVex] = ve[inVex] + p->weight;
            }
            p = p->next;
        }
    }

    if(count == vertexNum)
    {
        return true;
    }
    else
    {
        return false;
    }
}


bool ALGraph::GriticalPath()
{
    int resultStack[MAX_VERTEX];
    int resultTop;
    ArcNode *p;
    int i, count;
    int inVex, outVex;

    if(!TopologicalSort(resultStack, count))
    {
        return false;
    }
//    cout << "拓扑排序处理顺序为：";
//    for(i=0; i
//        cout << resultStack[i] << " ";
//    cout << endl;
//    cout << "ve数组值为：" << endl;
//    for(i=0; i
//        cout<<"ve[" << i << "]=" << ve[i] << endl;

    resultTop = count - 1;
    inVex = resultStack[resultTop--];

    for(i=0; i<vertexNum; i++)
    {
        vl[i] = ve[inVex];
    }

    while(resultTop != -1)
    {
        inVex = resultStack[resultTop--];
        p = adjList[inVex].firstEdge;
        while(p)
        {
            outVex = p->adjvex;
            if(vl[inVex]>vl[outVex] - p->weight)
            {
                vl[inVex] = vl[outVex] - p->weight;
            }
            p = p->next;
        }
    }

    //输出关键路径
    int sum = 0;
    queue< int > q;
    int head, tail;
    bool flag = true;
    for(inVex = 0; inVex<vertexNum; inVex++)
    {
        p = adjList[inVex].firstEdge;
        while(p)
        {
            outVex = p->adjvex;
            int weight = p->weight;
            int ee = ve[inVex];
            int el = vl[outVex]-weight;

            if(ee == el)
            {//当存在多条路径时
                if(flag)
                {
                   flag = false;
                   head = inVex+1;
                   tail = outVex+1;
                   sum += weight;
                }
                if(head == outVex+1)
                {
                    head = inVex+1;
                    sum += weight; //有多条路径时会算错
                }
                if(tail == inVex+1)
                {
                    tail = outVex+1;
                    sum += weight; //有多条路径时会算错
                }
                q.push(inVex+1);
                q.push(outVex+1);
                //cout << "<" << inVex+1 << ","<< outVex+1 << ">" << weight << " "; //因为是从0开始存，所以得+1再输出
            }
            p = p->next;
        }
    }
    printf("%d\n", sum);
    while(!q.empty())
    {
        printf("%d->", q.front());
        q.pop();
        printf("%d\n", q.front());
        q.pop();
    }
    return true;
}

int main()
{
    int vertex[MAX_VERTEX];
    int num, edge;

    cin>>num>>edge;
    for(int i=0; i<num; i++)
    {
        vertex[i] = i+1;
    }

    ALGraph graph(vertex, num, edge);
    graph.inputEdges();
    //graph.displayData();

    if(!graph.GriticalPath())
    {
        cout << 0;
    }
    return 0;
}

7-13 统计工龄

傻了，开始还准备排个序，直接只有0到50的工龄开个数组去记录不就好了。

7-14 电话聊天狂人

陈越姥姥讲聊天狂人

---

总结

因为实习和毕设的原因刷题就暂停了，之后大概率不会使用Java做题了