小样本学习(Few-shot Learning)之特征提取器-最大后验概率估计(MAP)、Wasserstein距离、最优传输-Sinkhorn算法
新的方向,在做特征提取器部分发现网上知识点分散,在此总结一下
小样本学习(Few-shot Learning)之特征提取器-最大后验概率估计(MAP)、Wasserstein距离、最优传输-Sinkhorn算法
- 1. 最大后验概率估计(MAP)
-
- 1.1 统计
- 1.2 贝叶斯公式(Bayes’ Theorem)
- 1.3 似然函数(likelihood function)和概率函数(probability function)
- 1.5 最大后验概率估计(MAP)
- 2. Wasserstein距离(Wasserstein distance)
-
- 2.1 KL散度
- 2.2 JS散度
- 2.3 Wasserstein距离
- 3. 最优传输-Sinkhorn算法
-
- 3.1 最优传输问题
- 3.2 Kantorovich relaxation
- 3.3 熵正则化
- 3.4 Sinkhorn算法
- 本文参考
1. 最大后验概率估计(MAP)
最大后验概率估计(Maximum A Posteriori, MAP)是一种常用的参数估计方法,要弄懂其原理,我们先从统计说起。
1.1 统计
Lary Wasserman 在 All of Statistics 的序言里有说过概率论和统计推断的区别:
The basic problem that we study in probability is:
Given a data generating process, what are the properities of the outcomes?
The basic problem of statistical inference is the inverse of probability: Given the outcomes, what can we say about the process that generated the data?
总结:
概率是已知模型和参数(生成数据的过程),推数据(结果)。
统计是已知数据(结果),推模型和参数(生成数据的过程)。
统计研究的问题是:已知一堆数据,如何利用这堆数据去预测模型和参数。
以猪为例。现在我买到了一堆肉,通过观察和判断,我确定这是猪肉(确定模型。在实际研究中,也是通过观察数据推测模型是/像高斯分布的、指数分布的、拉普拉斯分布的等等),然后,可以进一步研究,判定这猪的品种、喂养方式、猪棚的设计、是圈养猪还是跑山猪还是网易猪,等等(推测模型参数)。
现在我们知道了最大后验概率估计(Maximum A Posteriori, MAP)是一种统计领域的参数估计方法,那么具体如何实现?这需要我们理解贝叶斯思想。
1.2 贝叶斯公式(Bayes’ Theorem)
贝叶斯统计的重点:参数未知且不确定,因此作为随机变量,参数本身也是一个分布,同时,根据已有的信息可以得到参数θ的先验概率,根据先验概率来推断θ的后验概率。
贝叶斯估计:从**参数的先验知识和样本(数据)**出发。期望后延信息在真实的θ值处有一个尖峰。
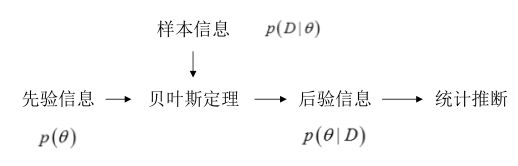
我们都知道贝叶斯公式(Bayes’ Theorem):
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) ( 1 ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} (1) P(A∣B)=P(B)P(B∣A)P(A)(1)
把B展开,可以写成:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ∣ A ) P ( A ) + P ( B ∣ ∼ A ) P ( ∼ A ) ( 2 ) P(A|B)=\frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|∼A)P(∼A)} (2) P(A∣B)=P(B∣A)P(A)+P(B∣∼A)P(∼A)P(B∣A)P(A)(2)
这个式子就很有意思了。
想想这个情况。一辆汽车(或者电瓶车)的警报响了,你通常是什么反应?有小偷?撞车了? 不。。 你通常什么反应都没有。因为汽车警报响一响实在是太正常了!每天都要发生好多次。本来,汽车警报设置的功能是,出现了异常情况,需要人关注。然而,由于虚警实在是太多,人们渐渐不相信警报的功能了。
贝叶斯公式就是在描述,你有多大把握能相信一件证据?(how much you can trust the evidence)
我们假设响警报的目的就是想说汽车被砸了。把 A A A计作“汽车被砸了”, B B B计作“警报响了”,带进贝叶斯公式里看。我们想求等式左边发生 A ∣ B A|B A∣B的概率,这是在说警报响了,汽车也确实被砸了。
汽车被砸引起(trigger)警报响,即 B ∣ A B|A B∣A。但是,也有可能是汽车被小孩子皮球踢了一下、被行人碰了一下等其他原因(统统计作 ∼ A ∼A ∼A),其他原因引起汽车警报响了,即 B ∣ ∼ A B|∼A B∣∼A。
那么,现在突然听见警报响了,这时汽车已经被砸了的概率是多少呢(这即是说,警报响这个证据有了,多大把握能相信它确实是在报警说汽车被砸了)?想一想,应当这样来计算。用警报响起、汽车也被砸了这事件的数量,除以响警报事件的数量(即为(1))。进一步展开,即警报响起、汽车也被砸了的事件的数量,除以警报响起、汽车被砸了的事件数量加上警报响起、汽车没被砸的事件数量(即为(2))。
思考(2),想让 P ( A ∣ B ) = 1 P(A|B)=1 P(A∣B)=1,即警报响了,汽车一定被砸了,该怎么做呢?
让 P ( B ∣ ∼ A ) P ( ∼ A ) = 0 P(B|∼A)P(∼A)=0 P(B∣∼A)P(∼A)=0即可。很容易想清楚,假若让 P ( ∼ A ) = 0 P(∼A)=0 P(∼A)=0,即杜绝了汽车被球踢、被行人碰到等等其他所有情况,那自然,警报响了,只剩下一种可能——汽车被砸了。这即是提高了响警报这个证据的说服力。
从这个角度总结贝叶斯公式:做判断的时候,要考虑所有的因素。 老板骂你,不一定是你把什么工作搞砸了,可能只是他今天出门前和太太吵了一架。
再观察(2)右边的分子, P ( B ∣ A ) P(B|A) P(B∣A)为汽车被砸后响警报的概率。姑且仍为这是1吧。
但是,若 P ( A ) P(A) P(A)很小,即汽车被砸的概率本身就很小,则 P ( B ∣ A ) P ( A ) P(B|A)P(A) P(B∣A)P(A)仍然很小,即(2)右边分子仍然很小, P ( A ∣ B ) P(A|B) P(A∣B)还是大不起来。
这里, P ( A ) P(A) P(A)即是常说的先验概率,如果 A A A的先验概率很小,就算 P ( B ∣ A ) P(B|A) P(B∣A)较大,可能 A A A的后验概率 P ( A ∣ B ) P(A|B) P(A∣B)还是不会大(假设 P ( B ∣ ∼ A ) P ( ∼ A ) P(B|∼A)P(∼A) P(B∣∼A)P(∼A)不变的情况下)。
从这个角度思考贝叶斯公式:一个本来就难以发生的事情,就算出现某个证据和他强烈相关,也要谨慎。证据很可能来自别的虽然不是很相关,但发生概率较高的事情。
例: 发现刚才写的代码编译报错,可是我今天状态特别好,这语言我也很熟悉,犯错的概率很低。因此觉得是编译器出错了。 ————别,还是先再检查下自己的代码吧。
1.3 似然函数(likelihood function)和概率函数(probability function)
在统计里面,似然函数和概率函数是两个不同的概念(其实也很相近就是了)。
之前我们说到:
概率是已知模型和参数(生成数据的过程),推数据(结果)。
统计是已知数据(结果),推模型和参数(生成数据的过程)。
对于这个函数: P ( x ∣ θ ) P(x|θ) P(x∣θ)。输入有两个: x x x表示某一个具体的数据; θ θ θ表示模型的参数。
如果 θ θ θ是已知确定的, x x x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点 x x x,其出现概率是多少。
如果 x x x是已知确定的, θ θ θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现 x x x这个样本点的概率是多少。
例如:
f ( x , y ) = x y f(x,y)=x^y f(x,y)=xy, 即 x x x的 y y y次方。如果 x x x是已知确定的(例如 x = 2 x=2 x=2),这就是 f ( y ) = 2 y f(y)=2^y f(y)=2y, 这是指数函数。
如果 y y y是已知确定的(例如 y = 2 y=2 y=2),这就是 f ( x ) = x 2 f(x)=x^2 f(x)=x2,这是二次函数。
同一个数学形式,从不同的变量角度观察,可以有不同的名字。
1.5 最大后验概率估计(MAP)
上一节我们说到了似然函数和概率函数的区别,这一节我们延续二者,说一说极大似然估计(MLE)和最大后验概率估计(MAP)。
在极大似然估计(MLE)中,我们求参数 θ \theta θ,使得似然函数 p ( X ∣ θ ) p(X|\theta) p(X∣θ)最大。
此时 θ \theta θ为一个待估模型参数,其为变量,未知。 X X X为现有数据集,已经确定。
假设有一个造币厂生产某种硬币,现在我们拿到了一枚这种硬币,想试试这硬币是不是均匀的。即想知道抛这枚硬币,正反面出现的概率(记为 θ θ θ)各是多少?
这是一个统计问题,回想一下,解决统计问题需要什么? 数据!
于是我们拿这枚硬币抛了10次,得到的数据( X X X)是:反正正正正反正正正反。我们想求的正面概率 θ θ θ是模型参数,而抛硬币模型我们可以假设是二项分布。
那么,出现实验结果 X X X(即反正正正正反正正正反)的似然函数是多少呢?
f ( X ∣ θ ) = ( 1 − θ ) × θ × θ × θ × θ × ( 1 − θ ) × θ × θ × θ × ( 1 − θ ) = θ 7 ( 1 − θ ) 3 = f ( θ ) f(X|θ)=(1−θ)×θ×θ×θ×θ×(1−θ)×θ×θ×θ×(1−θ)=θ^7(1−θ)^3=f(θ) f(X∣θ)=(1−θ)×θ×θ×θ×θ×(1−θ)×θ×θ×θ×(1−θ)=θ7(1−θ)3=f(θ)
注意,这是个只关于 θ θ θ的函数。而最大似然估计,顾名思义,就是要最大化这个函数。

在 θ = 0.7 θ=0.7 θ=0.7时,似然函数取得最大值。
这样,我们已经完成了对 θ θ θ的最大似然估计。即,抛10次硬币,发现7次硬币正面向上,最大似然估计认为正面向上的概率是0.7。
一些人可能会说,硬币一般都是均匀的啊! 就算你做实验发现结果是“反正正正正反正正正反”,我也不信 θ = 0.7 θ=0.7 θ=0.7。
这里就包含了贝叶斯学派的思想了——要考虑先验概率。 为此,引入了最大后验概率估计。
而最大后验估计(MAP)是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似,但是最大的不同时,最大后验估计的融入了要估计量的先验分布。故最大后验估计可以看做规则化的最大似然估计。
即最大似然估计是求参数 θ θ θ, 使似然函数 P ( X ∣ θ ) P(X|θ) P(X∣θ)最大。
最大后验概率估计则是想求 θ θ θ,使 P ( X ∣ θ ) P ( θ ) P(X|θ)P(θ) P(X∣θ)P(θ)最大,求得的 θ θ θ不单单让似然函数大, θ θ θ自己出现的先验概率也得大 。(这有点像正则化里加惩罚项的思想,不过正则化里是利用加法,而MAP里是利用乘法)
MAP其实是在最大化
P ( θ ∣ X ) = P ( X ∣ θ ) P ( θ ) P ( X ) , P(θ|X)=\frac{P(X|θ)P(θ)}{P(X)}, P(θ∣X)=P(X)P(X∣θ)P(θ),
不过因为 X X X是确定的(即投出的“反正正正正反正正正反”), P ( X ) P(X) P(X)是一个已知值,所以去掉了分母 P ( X ) P(X) P(X)(假设“投10次硬币”是一次实验,实验做了1000次,“反正正正正反正正正反”出现了n次,则 P ( X ) = n / 1000 P(X)=n/1000 P(X)=n/1000。总之,这是一个可以由数据集得到的值(独立可忽略))。最大化 P ( θ ∣ X ) P(θ|X) P(θ∣X)的意义也很明确, X X X已经出现了,要求 θ θ θ取什么值使 P ( θ ∣ X ) P(θ|X) P(θ∣X)最大。顺带一提, P ( θ ∣ X ) P(θ|X) P(θ∣X)即后验概率,这就是“最大后验概率估计”名字的由来。
最大后验概率估计是最大似然和贝叶斯估计的结合
这里需要说明,虽然从公式上来看 M A P = M L E ∗ P ( θ ) MAP=MLE*P(\theta) MAP=MLE∗P(θ),但是这两种算法有本质的区别,极大似然估计(MLE)将 θ \theta θ视为一个确定未知的值,而最大后验概率估计(MAP)则将 θ \theta θ视为一个随机变量。
对于投硬币的例子来看,我们认为(”先验地知道“) θ θ θ取0.5的概率很大,取其他值的概率小一些。我们用一个高斯分布来具体描述我们掌握的这个先验知识,例如假设 P ( θ ) P(θ) P(θ)为均值0.5,方差0.1的高斯函数,如下图:
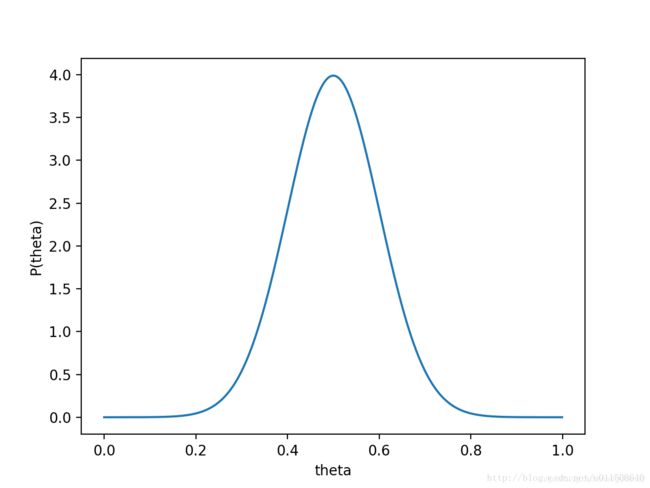
则 P ( X ∣ θ ) P ( θ ) P(X|θ)P(θ) P(X∣θ)P(θ)的函数图像为:
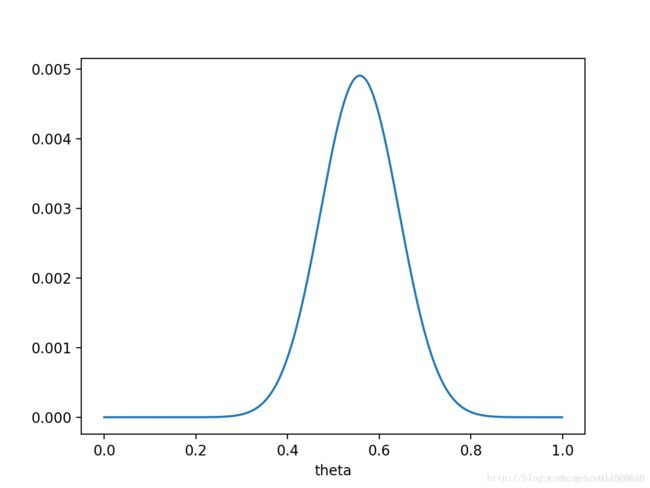
注意,此时函数取最大值时, θ θ θ取值已向左偏移,不再是0.7。实际上,在 θ = 0.558 θ=0.558 θ=0.558时函数取得了最大值。即,用最大后验概率估计,得到 θ = 0.558 θ=0.558 θ=0.558
最后,那要怎样才能说服一个贝叶斯派相信θ=0.7呢?你得多做点实验。。
如果做了1000次实验,其中700次都是正面向上,在 θ = 0.7 θ=0.7 θ=0.7时,似然函数取得最大值

如果仍然假设 P ( θ ) P(θ) P(θ)为均值0.5,方差0.1的高斯函数, P ( X ∣ θ ) P ( θ ) P(X|θ)P(θ) P(X∣θ)P(θ)的函数图像为:

在 θ = 0.696 θ=0.696 θ=0.696处, P ( X ∣ θ ) P ( θ ) P(X|θ)P(θ) P(X∣θ)P(θ)取得最大值。
这样,就算一个考虑了先验概率的贝叶斯派,也不得不承认得把 θ θ θ估计在0.7附近了。
2. Wasserstein距离(Wasserstein distance)
在各种机器学习算法中,距离的定义都是至关重要的,经常对算法的性能有极大的影响,也是设计算法时最需要考虑的几点之一。在很多情况下,我们最熟悉的L2距离就已经很好了,不过用高级数学找到更好的距离计算方式,有时就能更上一层楼.
2.1 KL散度
KL散度又称为相对熵,信息散度,信息增益。KL散度是是两个概率分布 P P P和 Q Q Q 差别的非对称性的度量。 KL散度是用来 度量使用基于 Q Q Q的编码来编码来自 P P P的样本平均所需的额外的位元数。 典型情况下, P P P表示数据的真实分布, Q Q Q表示数据的理论分布,模型分布,或 P P P的近似分布。
K L ( P ∣ ∣ Q ) = E x − P log P Q = ∫ x log P Q d x KL(P||Q)=E_{x-P}\log\frac{P}{Q}=\int_{x} \log\frac{P}{Q}\, {\rm d}x KL(P∣∣Q)=Ex−PlogQP=∫xlogQPdx
因为对数函数是凸函数,所以KL散度的值为非负数。
有时会将KL散度称为KL距离,但它并不满足距离的性质:
- KL散度不是对称的;
- KL散度不满足三角不等式。
2.2 JS散度
**JS散度(Jensen-Shannon)**度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。一般地,JS散度是对称的,其取值是0到1之间。
KL散度和JS散度度量的时候有一个问题:
如果两个分配 P , Q P,Q P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。
2.3 Wasserstein距离
Wasserstein距离度量两个概率分布之间的距离,定义如下:
W ( P 1 , P 2 ) = inf γ ∼ Π ( P 1 , P 2 ) E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] W(P_1,P_2)=\inf_{\gamma \sim \Pi (P_{1},P_{2})}E(x,y)∼\gamma[||x−y||] W(P1,P2)=γ∼Π(P1,P2)infE(x,y)∼γ[∣∣x−y∣∣]
∏ ( P 1 , P 2 ) \prod (P_1,P_2) ∏(P1,P2)是 P 1 P_{1} P1和 P 2 P_{2} P2分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布 γ \gamma γ,可以从中采样 ( x , y ) ∼ γ (x,y)∼\gamma (x,y)∼γ得到一个样本 x x x和 y y y,并计算出这对样本的距离 ∣ ∣ x − y ∣ ∣ ||x−y|| ∣∣x−y∣∣,所以可以计算该联合分布 γ \gamma γ下,样本对距离的期望值 E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] E(x,y)∼\gamma[||x−y||] E(x,y)∼γ[∣∣x−y∣∣]。 在所有可能的联合分布中能够对这个期望值取到的下界
inf γ ∼ Π ( P 1 , P 2 ) E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] \inf_{\gamma \sim \Pi (P_{1},P_{2})}E(x,y)∼\gamma[||x−y||] γ∼Π(P1,P2)infE(x,y)∼γ[∣∣x−y∣∣]
就是Wasserstein距离。
直观上可以把 E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] E(x,y)∼\gamma[||x−y||] E(x,y)∼γ[∣∣x−y∣∣]理解为在 γ \gamma γ这个路径规划下把 P 1 P_{1} P1挪到 P 2 P_{2} P2所需要的消耗。而Wasserstein距离就是在最优路径规划下的最小消耗。所以Wesserstein距离又叫Earth-Mover距离。
Wessertein距离相比KL散度和JS散度的优势在于:即使两个分布的支撑集没有重叠或者重叠非常少,仍然能反映两个分布的远近。而JS散度在此情况下是常量,KL散度可能无意义。
3. 最优传输-Sinkhorn算法
3.1 最优传输问题
最优传输(Optimal Transport)关键的一点是,要考虑怎样把多个数据点同时从一个空间映射到另一个空间上去,而不是只考虑一个数据点。
这里借用Computational Optimal Transport书中一个形象例子:把一堆沙子里的每一铲都对应到一个沙雕上的一铲沙子,怎么搬沙子最省力气,这就是个最优传输问题(注:这里“省力气”等于是cost function,现实中当然有很多不同的cost function来得到不同特点的传输)。
很明显能够看出最优传输和机器学习之间千丝万缕的关系,比如GAN本质上就是从输入的空间映射到生成样本的空间。
3.2 Kantorovich relaxation
要了解Kantorovich问题,首先我们先要知道蒙日(Monge)问题
找出从一个 measure到另一个measure的映射,使得所有 c ( x i , y j ) c(x_i,y_j) c(xi,yj)的和最小。当然 c c c是个cost function,根据具体应用定义。
这里的映射一定需要surjective(onto),也就是说 β β β上每个元素 y j y_j yj都至少又一个 x i x_i xi, T ( x i ) = y j T(x_i)=y_j T(xi)=yj。
Kantorovich relaxation可以说是原本蒙日问题的一个松弛版本
蒙日问题的原本定义中,一个measure中的每个元素都要对应到另一个measure的一个元素上,导致这个定义只能用来分析同等大小的measure (也就是说只能比较和最优化permutation)
同时,蒙日问题的约束条件, T α = β T\alpha=\beta Tα=β,要求对于measure α α α里的每一个元素,都对应到measure β β β里一个质量完全相等的元素上。
这个约束条件并不是线性的,于是蒙日问题很难求解。
于是就有了kantorovich relaxation,将原来的要求松弛,允许每个元素的质量分给目的分布里的多个元素,而不是蒙日问题里的一对一传输
这样我们的约束就变为以下公式:
![]()
这个约束不要求measure α , β α,β α,β里的元素一一对应,只需保证 α α α里每个元素的质量完全传走, β β β里每个元素也都收到正确的总质量就足够了。
这个简化的约束条件变为线性,相比原本蒙日问题求解难度大幅降低,这也是之后主要都用Kantorovich的重要原因
kantorovich 的传输可以用一个矩阵来表示, P i , j P_{i,j} Pi,j代表 a i a_i ai到 b j b_j bj的质量传输大小每个传输仍然需要保证质量守恒(2.10)
于是eq. 2.11给出了最优传输问题用kantorovich的定义:

这里 U U U是从 a a a到 b b b的所有可能传输 P P P的集合,而 P P P就是当前的传输
C C C仍然是cost matrix
当然原本的蒙日问题是kantorovich的一个特例,也就是说kantorovich是包含原本问题的
3.3 熵正则化
在大型数据集上进行最优传输时 ,时间复杂度是个非常重要的因素。
不过,在大部分应用情况下,求标准Kantorovich解是不必要的:如果我们利用正则化,改求近似解,那么最优传输的计算代价就大幅降低了。
使用正则化的最优传输问题用一系列矩阵乘法即可求解–这意味着最优传输可以充分享受GPU的矩阵加速效果,实用价值明显提升。
同时,正则化后的最优传输距离对输入的概率分布是完全连续的,并且能够系统式求导,在WGAN等方向上这点卓有成效。
正则化定义:
H ( P ) = d e f − ∑ i , j P i , j ( log ( P i , j − 1 ) ) H(P)\overset{\underset{\mathrm{def}}{}}{=}-\begin{matrix} \sum_{i,j}P_{i,j}(\log(P_{i,j}-1)) \end{matrix} H(P)=def−∑i,jPi,j(log(Pi,j−1))
H ( P ) H(P) H(P)即为正则化的代价函数,是整个概念的核心。
那么加上正则化的最优传输问题则变为
L C ϵ ( a , b ) = d e f m i n P ∈ U a , b < P , C > − ϵ H ( P ) L_C^\epsilon(a,b)\overset{\underset{\mathrm{def}}{}}{=}min_{P\in{U_{a,b}}}
这里的 ε ε ε(epsilon)是个正则化系数,它的大小决定正则化作用的强度,道理和神经网络里的正则化系数是完全一样的。
分析正则化的作用
∑ i , j P i , j = 1 \begin{matrix} \sum_{i,j}P_{i,j} =1\end{matrix} ∑i,jPi,j=1,所以 log ( P i , j ) < 0 \log(P_{i,j})<0 log(Pi,j)<0绝对成立
同样一个单位的质量转移,如果分布在少数的 P i , j P_{i,j} Pi,j上,每个 P i , j P_{i,j} Pi,j 取值较大,那么代价会大于将质量分布在多个 P i , j P_{i,j} Pi,j上,每个 P i , j P_{i,j} Pi,j取值很小。
换句话说,正则化鼓励利用多数小流量路径的传输,而惩罚稀疏的,利用少数大流量路径的传输,由此达到减少计算复杂度的目的。
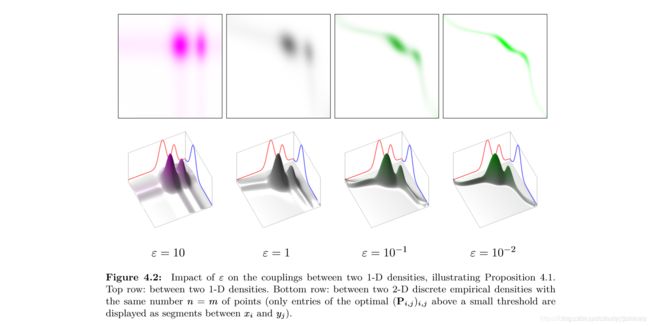
可以看到,在 ε ε ε取值较低时,传输集中使用少数路径,然而当 ε ε ε取值变大,正则化传输的最优解变得更加“扁平”,使用更多的路径进行传输。
3.4 Sinkhorn算法
在上一节里,我们介绍了加入熵正则化的最优传输问题–熵正则化通过限制最优传输问题解的复杂度,可以以大幅降低的复杂度得到最优传输问题的近似解。
不过,熵正则化仍然是一个概念,需要一个有效的算法,才能够释放它的潜力。
所以,在这一篇里,我们探索实际应用中十分常见的Sinkhorn算法。
得到Sinkhorn算法的第一步在于换一种方式表达正则化后的问题,详见
最优传输-Sinkhorn算法
本文参考
详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
Wasserstein_wiki
Maximum_likelihood_wiki
Computational Optimal Transport
Kantorovich relaxation
熵正则化