【并查集】【树】最近公共祖先LCA-Tarjan算法

最近公共祖先LCA

双链BT

如果每个结点都有一个指针指向它的父结点，于是我们可以从任何一个结点出发，得到一个到达树根结点的单向链表。因此这个问题转换为两个单向链表的第一个公共结点(先分别遍历两个链表得到它们的长度，并求出两个长度之差。在长的链表上先遍历若干个点之后，再同步遍历两个链表，知道找到相同的结点，或者一直到链表结束)。

BST

不用递归recursive，迭代iterative就行

public int query(Node t, Node u, Node v) {    
    int left = u.value;    
    int right = v.value;    
    Node parent = null;    

    //二叉查找树内，如果左结点大于右结点，不对，交换  
    if (left > right) {    
        int temp = left;    
        left = right;    
        right = temp;    
    }    

    while (true) {    
        //如果t小于u、v，往t的右子树中查找  
        if (t.value < left) {    
            parent = t;    
            t = t.right;    

        //如果t大于u、v，往t的左子树中查找  
        } else if (t.value > right) {    
            parent = t;    
            t = t.left;    
        } else if (t.value == left || t.value == right) {    
            return parent.value;    
        } else {    
            return t.value;    
        }    
    }    
}  

普通BT

单链递归

node* getLCA (node* root, node* node1, node* node2)  {  
    if(root == null)  
        return null;  
    if(root== node1 || root==node2)  
        return root;  

    node* left = getLCA(root->left, node1, node2);  
    node* right = getLCA(root->right, node1, node2);  

    if(left != null && right != null)  
        return root;  
    else if(left != null)  
        return left;  
    else if (right != null)  
        return right;  
    else   
        return null;  
}

Tarjan算法

首先，Tarjan算法是一种离线算法，也就是说，它要首先读入所有的询问（求一次LCA叫做一次询问），然后并不一定按
照原来的顺序处理这些询问。而打乱这个顺序正是这个算法的巧妙之处。看完下文，你便会发现，如果偏要按原来的顺序
处理询问，Tarjan算法将无法进行。

下面是算法的详细讲解

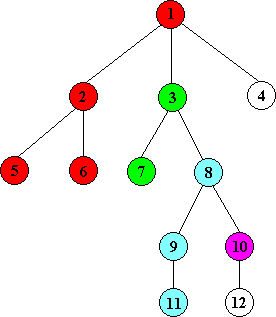
处理结点10的时候并查集的情况
（假设结点是按从左到右的顺序处理的）
与10的LCA是10的结点集合：{10}
与10的LCA是8结点集合：{8 9 11}
与10的LCA是3的结点集合：{3 7}
与10的LCA是1的结点集合：{1 2 5 6}
不属于任何集合的结点：4 12

　　Tarjan算法是利用并查集来实现的。它按DFS的顺序遍历整棵树。对于每个结点x，它进行以下几步操作：
计算当前结点的层号lv[x]，并在并查集中建立仅包含x结点的集合，即root[x]:=x。
依次处理与该结点关联的询问。
递归处理x的所有孩子。
root[x]:=root[father[x]]（对于根结点来说，它的父结点可以任选一个，反正这是最后一步操作了）。
　　现在我们来观察正在处理与x结点关联的询问时并查集的情况。由于一个结点处理完毕后，它就被归到其父结点所在的集合，所以在已经处理过的结点中（包括x本身），x结点本身构成了与x的LCA是x的集合，x结点的父结点及以x的所有已处理的兄弟结点为根的子树构成了与x的LCA是father[x]的集合，x结点的父结点的父结点及以x的父结点的所有已处理的兄弟结点为根的子树构成了与x的LCA是father[father[x]]的集合……（上面这几句话如果看着别扭，就分析一下句子成分，也可参照右面的图）假设有一个询问(x,y)（y是已处理的结点），在并查集中查到y所属集合的根是z，那么z就是x和y的LCA，x到y的路径长度就是lv[x]+lv[y]-lv[z]*2。累加所有经过的路径长度就得到答案。
　　现在还有一个问题：上面提到的询问(x,y)中，y是已处理过的结点。那么，如果y尚未处理怎么办？其实很简单，只要在询问列表中加入两个询问(x,y)、(y,x)，那么就可以保证这两个询问有且仅有一个被处理了（暂时无法处理的那个就pass掉）。而形如(x,x)的询问则根本不必存储。
　　如果在并查集的实现中使用路径压缩等优化措施，一次查询的复杂度将可以认为是常数级的，整个算法也就是线性的了。
　　另外，实现上还有一点技巧：树的边表和询问列表的存储可以用数组模拟的链表来实现。

最近公共祖先LCA Tarjan算法

hdu2586 How far away

题意

给定一棵树，每条边都有一定的权值，q次询问，每次询问某两点间的距离。

解法

这样就可以用LCA来解，首先找到u, v 两点的lca，然后计算一下距离值就可以了。这里的计算方法是，记下根结点到任意一点的距离dis[]，这样ans = dis[u] + dis[v] - 2 * dis[lca(v, v)]了，这个表达式还是比较容易理解的。。

poj1470 Closest Common Ancestors

这道题和上面那道一样，很典型的LCA问题，不过读入有点麻烦，求的是每个点被作为最近公共祖先的次数

并查集

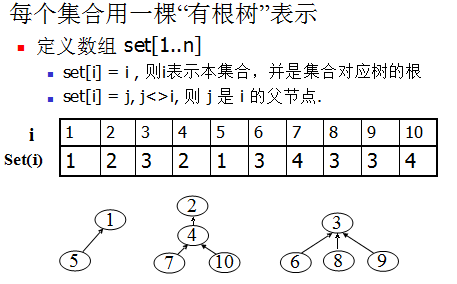
畅通工程(HDOJ-1232)

题目描述：

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？
　　

分析：

若每个城市之间有且仅有一条道路相连，那这肯定是一棵树了。边数 = 节点数 -1 ，只要我们知道城市被分成的集合数ans，要修的道路就是ans-1 ，下面贴出经过路径压缩的并查集。
　　

UVA - 10608-Friends

题目大意：

给定n个人，和m个关系，m个关系代表谁和谁认识之类的，求这样的关系中，朋友圈人数最多的人数。

解题思路：

这题用并查集来判断这两个人是否属于同一个朋友圈，刚开始每个人自己形成一个朋友圈，所以每个朋友圈人数为1，然后每碰到一个关系就判断这两个人p1,p2是否属于同一个朋友圈，如果不是，就把其中一个的f[t]（t=find(p1)为这个圈子的根）改为另一个朋友圈的根r=find(p2)，然后把以r为根的这个圈子的人数c[r]加上以t为根的圈子的朋友数c[t]。这样最后只要找f[i] == i（这样的i是根）的这样的圈子的朋友数，找最大的c[i]。