根据广义表创建二叉树以及层次遍历
【问题描述】 考研真题:给定一颗二叉树,要求从下至上按层遍历二叉树,每层的访问顺序是从左到右,每一层单独输出一行。
【输入形式】 广义表表示的二叉树,结点元素类型为整型,且都大于0,例如:1( 2( 3 ( 4, 5 ) ), 6( 7, 8( 9, 10 ) ) )
【输出形式】 从下至上,打印每一层的结点元素值,元素间以空格隔开。每层的访问顺序是从左到右,每一层单独输出一行。
【样例输入】 1(2(3(4,5)),6(7,8(9,10))),字符串内没有空格
【样例输出】
4 5 9 10
3 7 8
2 6
1
审题:
1.根据广义表创建一颗二叉树
2.层次遍历这个二叉树
首先解决第一个问题——根据广义表创建二叉树。
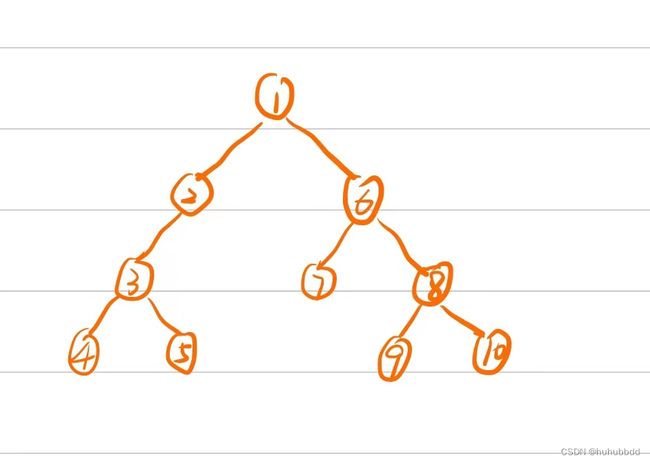
题目中给的示例1(2(3(4,5)),6(7,8(9,10))),转化为二叉树如下图所示。
我们可以看到,广义表形式的二叉树其实结构上是_(_( ),_( )),第一个下划线代表双亲结点,第二个和第三个下划线代表孩子结点,孩子结点有可能不存在。
举个例子图中的1、2、6,在原广义表中是1(2(3(4,5)),6(7,8(9,10)))。
又比如图中的3、4、5,在原广义表中是1(2(3(4,5)),6(7,8(9,10)))。
并且,这个结构是层层嵌套的,递归的。
当孩子结点不存在括号的时候,递归结束,也就是3、4、5那种情况。
明白这些之后,那么找到分割左右子树的逗号,就非常重要了。
这里采用栈结构进行括号匹配,如果匹配到逗号时,栈里只有一个左括号,证明这个逗号就是我们要找的逗号。
还有一个值得注意的点是,我们的数据并不全是个位数,所以还要考虑多位数的时候,怎么识别它们。
BiNode* Bitree::create(char *s,int i,int j)//i,j分别指向根节点数字和最后一个右括号
{
if(i<=j)
{
BiNode *r=new BiNode;
int t=i;
while(1)
{
if(s[t]<'0'||s[t]>'9')
break;
t++;
}
int sum=0;
for(int k=i;k<=t-1;k++)
{
sum=sum*10+s[k]-'0';//不能写+=
}
r->data=sum;
if(i==j||j==t-1)
{
return r;
}
else{
int rr=i+1;
int flag=0;//判断有无逗号存在
Stack st;//括号匹配专用栈
while(rr<=j)//找到分割左右子树的逗号位置
{
switch(s[rr])
{
case '(':st.push(s[rr]);break;
case ')':st.pop();break;
}
if(s[rr]==','&&st.data[st.top]=='('&&st.top==0)
{
flag=1;
break;
}
rr++;
}
if(flag)
{
r->lf=create(s,i+2,rr-1);
r->rt=create(s,rr+1,j-1);
}
else
{
r->lf=create(s,i+2,rr-2);
r->rt=NULL;
}
}
return r;
}
else
return NULL;
}创建之后,层次遍历这个二叉树顾名思义就是一层一层的来
因为题目要求把树的层次倒过来输出,所以我选择首先把这棵树存进二位数组里,再遍历。
所以在层次遍历的同时还要求二叉树的宽度和深度
int tree[N][N]={0};
int width[N]={0};//记录第n层的宽度
int depth=0;//记录深度
void Bitree::bfs()
{
Queue q;int i=0,j=0;
q.enterQueue(*root);
int c=1;//上一层最右侧de后一位
while(q.len!=0)
{
BiNode temp=q.outQueue();
tree[i][j++]=temp.data;
if(temp.lf!=NULL)
q.enterQueue(*temp.lf);
if(temp.rt!=NULL)
q.enterQueue(*temp.rt);
if(q.fr==c)
{
c=q.re;
width[i]=j;
i++;
j=0;
}
}
depth=i;
}
void Bitree::output()
{
for(int i=depth-1;i>=0;i--)
{
for(int j=0;j最后完整代码如下:
#include
#include
#define N 50
using namespace std;
//层次遍历二叉树
//根据广义表创建二叉树
class BiNode
{
public:
BiNode *lf,*rt;
int data;
BiNode():lf(NULL),rt(NULL){}
};
class Bitree
{
public:
BiNode *root;
Bitree():root(NULL){}
BiNode* create(char *s,int i,int j);
void print(BiNode*);
void bfs();
void output();
};
class Stack
{
public:
int top;
char data[N];
Stack():top(-1){}
void push(char ch)
{
if(top'9')
break;
t++;
}
int sum=0;
for(int k=i;k<=t-1;k++)
{
sum=sum*10+s[k]-'0';//不能写+=
}
r->data=sum;
if(i==j||j==t-1)
{
return r;
}
else{
int rr=i+1;
int flag=0;//判断有无逗号存在
Stack st;//括号匹配专用栈
while(rr<=j)//找到分割左右子树的逗号位置
{
switch(s[rr])
{
case '(':st.push(s[rr]);break;
case ')':st.pop();break;
}
if(s[rr]==','&&st.data[st.top]=='('&&st.top==0)
{
flag=1;
break;
}
rr++;
}
if(flag)
{
r->lf=create(s,i+2,rr-1);
r->rt=create(s,rr+1,j-1);
}
else
{
r->lf=create(s,i+2,rr-2);
r->rt=NULL;
}
}
return r;
}
else
return NULL;
}
void Bitree::print(BiNode *p)
{
if(p!=NULL)
{
cout<data;
print(p->lf);
print(p->rt);
}
}
int tree[N][N]={0};
int width[N]={0};//记录第n层的宽度
int depth=0;//记录深度
void Bitree::bfs()
{
Queue q;int i=0,j=0;
q.enterQueue(*root);
int c=1;//上一层最右侧de后一位
while(q.len!=0)
{
BiNode temp=q.outQueue();
tree[i][j++]=temp.data;
if(temp.lf!=NULL)
q.enterQueue(*temp.lf);
if(temp.rt!=NULL)
q.enterQueue(*temp.rt);
if(q.fr==c)
{
c=q.re;
width[i]=j;
i++;
j=0;
}
}
depth=i;
}
void Bitree::output()
{
for(int i=depth-1;i>=0;i--)
{
for(int j=0;j