InfoGraph

Paper : InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization
Code :

摘要

作者使用 Deep Infomax 的方法来学习网络的图表示，并提出了自监督学习版本的训练方法 InfoGraph 与非监督学习版本的训练方法 InfoGraph* ，两者之间的差别在于 InfoGraph* 损失函数多了一项防止发生 negative transfer 。

Mutual Information

互信息定义为
$$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$$

其中 $H(\cdot )$ 表示随机变量的熵，$I(X;Y)$ 的直观解释是已知随机变量 $Y$ 时会使 $X$ 的不确定度减少多少，用于描述随机变量 $X$ 与随机变量 $Y$ 之间的相关性。计算方法如下所示

$$I(X;Y)=\sum _{X\sim \mathcal{X}}\sum _{Y\sim \mathcal{Y}}p(X,Y)\log \frac{p(X,Y)}{p(X)p(Y)}$$

互信息与KL散度具有如下性质

$$\begin{gathered} I(X;Y)=\sum _{Y\sim \mathcal{Y}}p(Y)\sum _{X\sim \mathcal{X}}p(X|Y)\log \frac{p(X|Y)}{p(X)} \\ =\sum _{Y\sim \mathcal{Y}}p(Y)D_{KL}(p(X|Y)||p(X)) \\ ={\mathbb{E}}_Y[D_{KL}(p(X|Y)||p(X))] \end{gathered}$$

InfoGraph

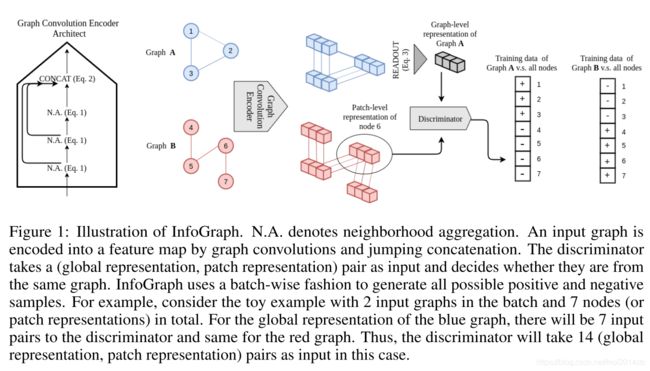
经过GNN网络中的若干层卷积，图上的点特征表示可以看作是对每个点感受野内的子图进行编码，最大化图表示与每个节点的隐变量之间的互信息可以看作是使图表示学习到图中每个子结构共有的特性。

首先对GNN进行形式化定义，GNN中第k层执行的操作是

$$h_v^{(k)}={\text{Combine}}^{(k)}(h_v^{(k-1)},{\text{Aggregate}}^{(k)}(\{h_v^{(k-1)},h_u^{(k-1)},e_{uv}|u\in \mathcal{N}(u)\}))$$

使用 $\varphi$ 表示GNN的参数，定义表示节点 $u$ 在不同的感受野下的隐变量为

$$h_{\varphi }^u=\text{Concat}(\{h_u^{(k)}{\}}_{k=1}^K)$$

定义使用读出层读出所有的节点表示获得的图表示为

$$H_{\varphi }(G)=\text{Readout}(\{h_{\varphi }^u{\}}_{u=1}^N)$$

很难直接在不同的空间上定义互信息，因此采用一种迂回的方式，如果对于输入 $x$ 与输出 $y(x)$，之间的互信息较大，那么对于任一与 $x$ 同分布但是与 $x$ 不同的输入 $x^{\prime }$，那么识别器应当很轻易的区分出来 $y(x)$ 与 $y(x^{\prime })$ 之间存在差异。因此，定义 $T_{\psi }$ 表示互信息评估用的区分器(discriminator)，其中 $\psi$ 表示区分器中的参数，InfoGraph 的目标是学习到

$$\varphi ,\psi =\arg \underset{\varphi ,\psi }{\max }\sum _{G\in \mathcal{G}}\frac{1}{|G|}\sum _{u\in G}{I}_{\varphi ,\psi }(h_{\varphi }^u;H_{\varphi }(G))$$

其中互信息定义为

$$I_{\varphi ,\psi }(h_{\varphi }^u;H_{\varphi }(G))={\mathbb{E}}_x[-\text{softplus}(-T_{\psi }(h_{\varphi }^u(x),H_{\varphi }(x)))]-{\mathbb{E}}_{x,x^{\prime }}[\text{softplus}(T_{\psi }(h_{\varphi }^u(x^{\prime }),H_{\varphi }(x)))]$$

其中 $\text{softplus}(x)=\ln (1+e^x)$，在训练时，使用batch中所有图实例的全局和局部点特征表示的所有可能组合来生成负样本。

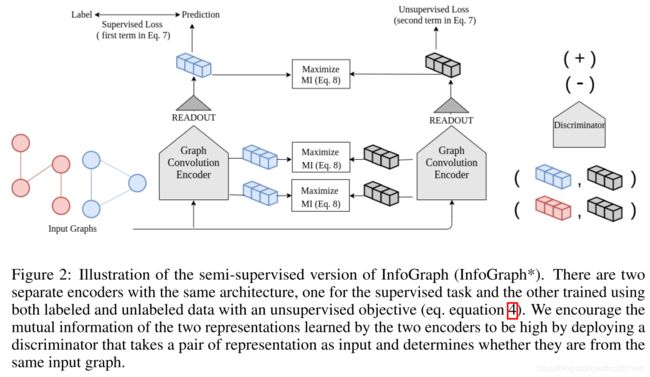
InfoGraph*

InfoGraph* 是 InfoGraph 的半监督版本，如果直接使用 InfoGraph 到半监督任务中，那么损失函数定义为

$$\mathcal{L}=\sum _{i=1}^{|{\mathcal{G}}_L|}{\mathcal{L}}_{\text{supervised}}(y_{\varphi }(G_i),y_i)+\lambda \sum _{i=1}^{|{\mathcal{G}}_L|+|{\mathcal{G}}_U|}{\mathcal{L}}_{\text{unsupervised}}(h_{\varphi }(G_i);H_{\varphi }(G_i))$$

其中无监督学习部分的损失函数定义为

$${\mathcal{L}}_{\text{unsupervised}}(h_{\varphi }(G_i);H_{\varphi }(G_i))=\frac{1}{|G_i|}\sum _{u\in G_i}{I}_{\varphi ,\psi }(h_{\varphi }^u;H_{\varphi }(G_i))$$

为了防止发生 negative transfer ，即互信息与监督学习的优化方向不同，对监督学习和非监督学习部分分别在不同的参数上进行学习，并通过互信息监督两边学习到的图表示一致

$$\begin{gathered} \mathcal{L}=\sum _{i=1}^{|{\mathcal{G}}_L|}{\mathcal{L}}_{\text{supervised}}(y_{\varphi }(G_i),y_i)+{\lambda }_1\sum _{i=1}^{|{\mathcal{G}}_L|+|{\mathcal{G}}_U|}{\mathcal{L}}_{\text{unsupervised}}(h_{\phi }(G_i);H_{\phi }(G_i)) \\ -{\lambda }_2\sum _{i=1}^{|{\mathcal{G}}_L|+|{\mathcal{G}}_U|}\frac{1}{|G_i|}\sum _{k=1}^{K}I(H_{\varphi }^k(G_i);H_{\phi }(G_i)) \end{gathered}$$

这种损失函数定义方式可以类比于学生-教师模型。在实际训练过程中，随机采样编码层来进行互信息最大化。

总结

这篇论文中的实验部分个人觉得做的很有问题，它比较的方法要么就和GNN没啥关系，要么就是比较老的GNN自监督学习的方法，而且看上去没有做消融实验，使用的GNN结构还是表示能力很强的GIN，结果没有太强的说服力。