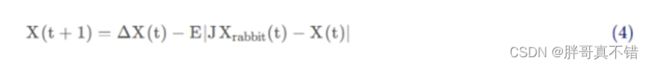Python实现哈里斯鹰优化算法(HHO)优化支持向量机回归模型(SVR算法)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

---

---

1.项目背景

---

       2019年Heidari等人提出哈里斯鹰优化算法(Harris Hawk Optimization, HHO)，该算法有较强的全局搜索能力，并且需要调节的参数较少的优点。

---

      本项目通过HHO哈里斯鹰优化算法寻找最优的参数值来优化支持向量机回归模型。

---

2.数据获取

---

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

---

编号	变量名称	描述
1	x1
2	x2
3	x3
4	x4
5	x5
6	x6
7	x7
8	x8
9	x9
10	y	因变量

---

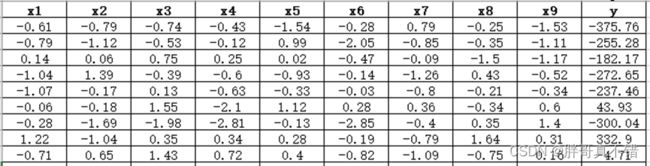
数据详情如下(部分展示)：

---

3.数据预处理

3.1 用Pandas工具查看数据

---

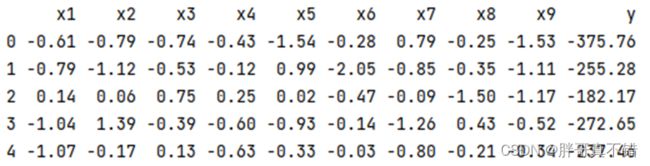
使用Pandas工具的head()方法查看前五行数据：

---

关键代码：

3.2数据缺失查看

---

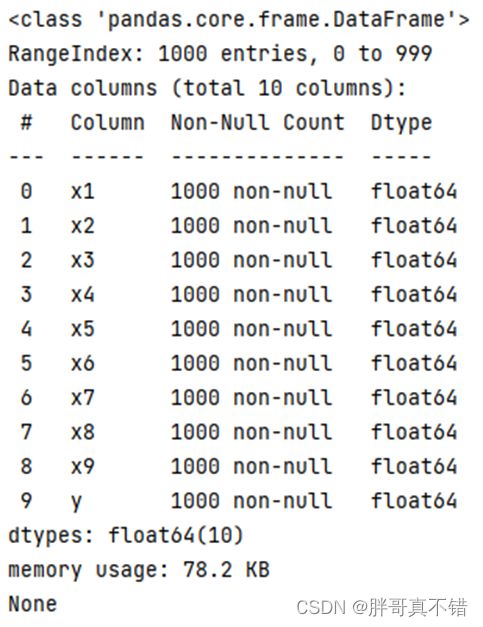
使用Pandas工具的info()方法查看数据信息： 

---

---

从上图可以看到，总共有10个变量，数据中无缺失值，共1000条数据。

关键代码：  

---

 

3.3数据描述性统计

---

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

---

关键代码如下：    

4.探索性数据分析

4.1 y变量直方图

---

用Matplotlib工具的hist()方法绘制直方图：

---

---

从上图可以看到，y变量主要集中在-200~200之间。

---

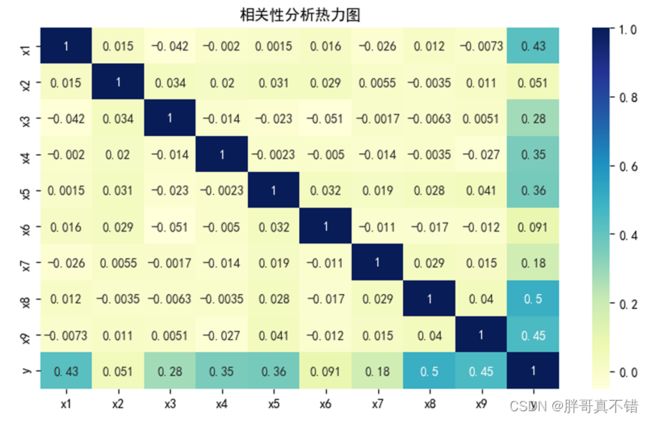
4.2 相关性分析

 

---

从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

---

5.特征工程

5.1 建立特征数据和标签数据

---

关键代码如下：

---

5.2 数据集拆分

---

通过train_test_split()方法按照80%训练集、20%测试集进行划分，关键代码如下：

---

6.构建HHO哈里斯鹰优化算法优化支持向量机回归模型

---

主要使用HHO哈里斯鹰优化算法优化SVR算法，用于目标回归。

---

6.1 算法介绍

---

     说明：HHO算法介绍来源于网络，供参考,需要更多算法原理，请自行查找资料。

算法原理：

---

哈里斯鹰随机栖息在某个地方，通过2种策略找到猎物：

---

 

---

      其中，X(t)、X(t+1)分别为分别为当前和下一次迭代式时个体的位置，t为迭代次数，Xrand(t)  为随机选出的个体位置，Xrabbit(t)  为猎物位置，即拥有最优适应度的个体位置，r1 , r2 ，r3 ，r4 ，q都是[0,1]之间的随机数。q用来随机选择要采用的策略，Xm(t)  为个体平均位置，表达式为：

---

---

其中，Xk(t)  为种群中第k个个体的位置，M为种群规模。

---

搜索与开发的转换

---

HHO 算法根据猎物的逃逸能量在搜索和不同的开发行为之间转换，逃逸能量定义为：

---

---

       其中，E0 是猎物的初始能量，为 [-1,1] 之间的随机数，每次迭代时自动更新，t为迭代次数，T 为最大迭代次数。当|E|≥1 时进入搜索阶段，|E|<1当时进入开发阶段。

---

开发阶段

---

       定义r为[0,1] 之间的随机数，用于选择不同的开发策略。当0.5 ≤ |E| < 1 且r ≥ 0.5 时，采取软围攻策略进行位置更新：

---

 

---

   其中，ΔX(t) = Xrabbit(t)  -X(t)表示猎物位置与个体当前位置的差值，J为 [0, 2] 之间的随机数。

---

当|E|<0.5且r ≥ 0.5 时采取硬围攻策略进行位置更新：

---

---

当0.5 ≤ |E| < 1 且r < 0.5时，采取渐近式快速俯冲的软包围策略进行位置更新：

---

---

其中，f()为适应度函数，S为 2 维随机向量，元素为[0,1] 之间的随机数，LF() 是莱维飞行的数学表达式。

---

当|E|<0.5且r < 0.5 时，采取渐近式快速俯冲的硬包围策略进行位置更新：

---

---

算法步骤：

---

步骤 1：种群初始化。根据搜索空间每一维的上界和下界，初始化每个个体。

步骤 2：计算初始适应度。将适应度最优的个体位置设为当前猎物位置。

步骤 3：位置更新。先通过更新猎物逃逸能量，然后根据逃逸能量和生成的随机数执行搜索或开发行为中对应的位置更新策略。

步骤 4：计算适应度。计算位置更新后的个体适应度，并与猎物适应度值进行比较，若位置更新后的个体适应度值优于猎物，则以适应度

值更优的个体位置作为新的猎物位置。

重复步骤 3 和步骤 4，当算法迭代次数达到最大迭代次数时。输出当前猎物位置作为目标的估计位置。

---

6.2 HHO哈里斯鹰优化算法寻找最优参数值

关键代码：

---

迭代过程：

---

---

 最优参数：

6.3 最优参数值构建模型 

编号	模型名称	参数
1	支持向量机回归模型	C= 1.0
2		gamma= 0.31188138371137797

7.模型评估

7.1 评估指标及结果

---

评估指标主要包括可解释方差值、平均绝对误差、均方误差、R方值等等。

---

模型名称	指标名称	指标值
测试集
支持向量机回归模型	R方	1.0
	均方误差	0.3751
	可解释方差值	1.0
	平均绝对误差	0.4897

---

从上表可以看出，R方1.0，为模型效果较好。

关键代码如下：

---

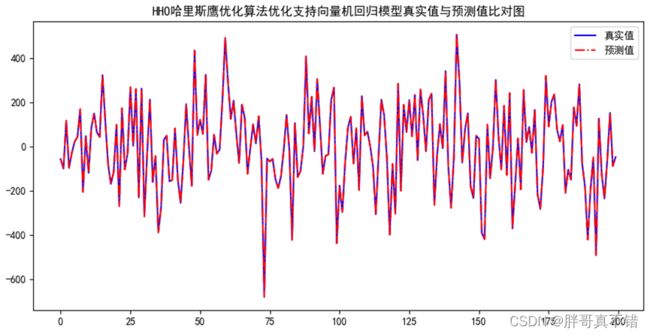
7.2 真实值与预测值对比图 

---

从上图可以看出真实值和预测值波动基本一致，模型拟合效果良好。

---

  

8.结论与展望

---

       综上所述，本文采用了HHO哈里斯鹰优化算法寻找支持向量机SVR算法的最优参数值来构建回归模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。 

---

本次机器学习项目实战所需的资料，项目资源如下：

项目说明：
链接：https://pan.baidu.com/s/1c6mQ_1YaDINFEttQymp2UQ 
提取码：thgk