广义典型相关分析_广义线性模型（GLM）概述及负二项回归应用举例和R计算

广义线性模型(GLM)概述及负二项回归应用举例和R计算 前述简介了几种一般线性模型(general linear model)，如简单线性回归 、多项式回归 、多元线性回归 等，它们基于普通最小二乘法(ordinary least square，OLS)的原理拟合自变量和响应变量的线性关系，目标是通过减少响应变量的观测值与拟合值的差值来获得模型参数，使残差平方和最小。因此一般线性模型的一个常见假设是响应变量服从正态分布，良好的正态分布可以使通过最小平方法估计的模型参数(截距、回归系数、拟合优度等)以及通过F检验获取的显著性等更为精确和稳定。 尽管在很多的实际应用中，为了不将问题考虑得那么复杂，经常放松对正态性的假设，常见于趋势描述、简单的变量效应解释等。 但若正态性偏离程度非常明显，使用一般线性模型的参数估计可能就不是很好。 其它一些情况，响应变量可能并非连续变量，而归属于计数型、类别型或因子型，此时使用一般线性模型也并不合理。 这些情况使得一般线性模型难以解释问题。 广义线性模型( generalize linear model ， GLM )扩展了线性模型的框架，它允许非正态响应变量的分析。从概念上讲，广义线性模型是一类服务于一组来自指数分布族的响应变量的模型框架，正态分布、指数分布、伽马分布、卡方分布、贝塔分布、伯努利分布、二项分布、负二项分布、多项分布、泊松分布、集合分布等都属于指数分布族。它们覆盖了生物学数据类型的更大范围，因此广义线性模型也广泛用于生物学领域的数据分析中。

广义线性模型的一般形式

先来看一般线性模型的表达式。对响应变量Y和p个自变量X1…Xp间的关系进行建模，则关系的形式为：

等式表明响应变量的条件均值是自变量的线性组合。β₀是截距项，β_j是自变量X_j的回归系数(斜率)，μ_Y是拟合的Y观测值分布的均值。式中假设Y呈正态分布。

推广到广义线性模型，其概括形式为：

g(μ_Y)代表了条件均值的函数(指数、泊松、二项式、负二项等)，响应变量Y服从指数分布族中的某种分布(不局限于正态性)。根据Y的实际分布选择合适的回归函数，便可以推导给定形式的广义线性回归模型的参数值。因此，广义线性模型框架内也涵括了许多非线性函数的存在。

尽管涵括了更多类型，但广义线性回归仍建立在响应变量尽可能满足特定分布的前提下，并根据分布特征选择合适的回归子类，若模型选择不合适，同样会使得统计功效较低。

广义线性模型的常见类别举例

负二项回归简介

广义线性模型框架内涵括的回归类型非常多，一篇内容无法全部介绍一遍。本篇就主要以其中一种常见类别，负二项回归(negative binomial regression)，举例简介广义线性模型在生物学数据中的应用，以及R语言计算。

生物学数据中很常见计数型数据，例如基因表达值、物种个体丰度等，这些数据通常也偏离正态性，常规的统计方法如t检验、一般线性模型等难以适用。在以前，用于计数型响应变量的基本回归模型是泊松(Poisson)回归，但由于计数数据的复杂性，经常出现过大离差(over-dispersion)或过小离差(under-dispersion)等问题，使得泊松回归有时不尽如人意。

泊松回归也是广义线性模型的一种子类，但现在更多被负二项回归取代。负二项回归是泊松回归的推广，可以很好的解决过大离差问题，且被实践证明非常有效，因此广泛用于计数型响应变量的生物统计领域。

举个例子，基于二、三代测序获得的基因表达值通常以reads count值等表示，就是典型的计数型数据。要计算基因表达值这类计数型数值在组间的差异，常规的t检验等方法的统计功效会降低，这时负二项回归就是很好的选择。这也是那些总所周知的基因表达分析R包如edgeR、DESeq2等广为流行的原因，它们的原理就是负二项回归。edgeR、DESeq2也广泛用于微生物组数据分析中，同样归因于基于测序得到的OTU/ASV都是整数型变量，可以视为物种个体计数来看待(但仅限于整数数值的丰度计算，小数型的相对丰度运行edgeR、DESeq2时会直接报错，负二项回归不能用于纯小数)。

上述是用在差异计算上的举例。当然作为回归模型的一种，更广泛的使用肯定是建模。例如生态学数据分析中，由于物种丰度通常表示为物种计数，负二项回归常见于环境和物种关系、物种和物种关系等的建模，解释环境效应、生物过程或种间关系等。

总之，使用到负二项回归的情景非常多。关于负二项回归的公式就不提了，自己也看着头晕，关键知道怎样使用。下文就列举一篇文献中的案例吧，帮助大致了解它是怎样在实际场景中应用的。

广义线性模型的应用举例

一个负二项回归在生物学数据分析中的应用案例解读

节选自 Benesh 和 Kalbe ( 2016 )的一项研究。非随机的物种关联模式广泛存在于寄生虫群落和宿主关系中，特定的物种关联模式与群落结构过程密不可分，例如宿主行为、交叉免疫、种间竞争；以及种内性状的变化，例如种群增长或抗原性。文中的部分内容中，作者评估了寄生虫 Schistocephalus solidu s 侵染三刺鱼 Gasterosteus aculeatus 后，三刺鱼表现出的对另一种寄生虫 Diplostomum pseudospathaceum 二次侵染的敏感性的影响和效应。    

S. solidus存在条件、三刺鱼性状等对D. pseudospathaceum侵染三刺鱼的影响

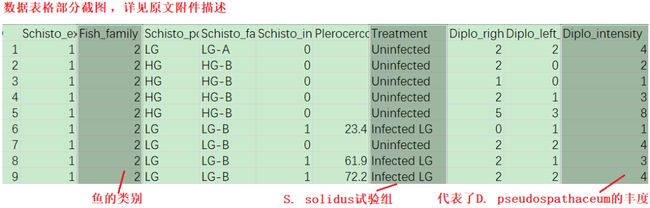
实验室环境下，作者设置了4种S. solidus试验条件：Control，三刺鱼未暴露于S. solidus，该组用作对照；Uninfected，三刺鱼暴露于S. solidus但未受到侵染；Infected LG，三刺鱼受到低生长速率的S. solidus的侵染；Infected HG，三刺鱼受到高生长速率S. solidus的侵染。并同时测量了三刺鱼类别、长度、重量、性别等属性特征，以及试验结束时观测到的鱼体中D. pseudospathaceum的丰度。

作者选择广义线性模型用于对S. solidus试验条件、三刺鱼体重、性别、类别(这4种变量作为自变量)和D. pseudospathaceum丰度(作为响应变量)关系的建模，以比较各因素对D. pseudospathaceum侵染三刺鱼的影响。作者在文中也提及了选择广义线性模型的原因，它可以很好地解释响应变量(寄生虫丰度)的典型超分散现象(Shaw and Dobson, 1995)，特别是生态学数据普遍存在非正态特征，并且在满足特殊分布时与基于距离矩阵的多变量方法相比通常具有更高的统计功效和更低的偏差(Warton et al, 2012)。R语言mvabund包用于拟合广义线性模型，为了获得稳健的结果，作者选择了负二项回归，并基于9999次自举估计显著性。 

简单概括结果，三刺鱼体重(GLM，p=0.14)和性别(p=0.16)都与D. pseudospathaceum的侵染无关，三刺鱼类别(p<0.001)和S. solidus试验条件(p<0.001)对D. pseudospathaceum侵染的影响显著。试验组Uninfected(三刺鱼暴露于S. solidus但未受到侵染)、LG(三刺鱼受到低生长速率的S. solidus的侵染)和HG(三刺鱼受到高生长速率S. solidus的侵染)相比，HG组中观察到的D. pseudospathaceum丰度更高，表明较高的S. solidus侵染程度也会同时加重D. pseudospathaceum对三刺鱼的二次侵染。

原文图1，展示了在实验室环境中，4种S. solidus试验条件下的三刺鱼中观察到的D. pseudospathaceum侵染程度。

三刺鱼中S. solidus生长状态对其受D. pseudospathaceum侵染敏感性的影响

在上述结果中，已知三刺鱼体重、性别对D. pseudospathaceum侵染无影响，故排除它们后，重新对S. solidus试验条件、三刺鱼类别和D. pseudospathaceum丰度关系的建模。同时已知较高的S. solidus侵染程度也会加重D. pseudospathaceum侵染，因此作者期望进一步在已感染S. solidus的三刺鱼中，评估S. solidus生长对D. pseudospathaceum侵染的敏感性的效应，随后还将S. solidus重量(反映了S. solidus生长)作为新的自变量添加在负二项回归中。

结果显示，考虑了S. solidus重量的影响后，模型精度有轻微提升。S. solidus重量的效应是显著的(GLM，p=0.041)，且回归系数为正(coefficient=0.007)，表明三刺鱼对D. pseudospathaceum侵染的敏感程度也会随S. solidus生长而加重，这个现象和已知较高的S. solidus侵染程度能够加重D. pseudospathaceum侵染的趋势是一致的。但是这种效应强烈依赖于三刺鱼的类别，当在模型中删除三刺鱼类别的效应时，S. solidus重量对D. pseudospathaceum丰度的关系不再显著(p=0.9)。

此外，作者还在负二项回归中添加了S. solidus试验条件和S. solidus重量的交互效应分析，但结果显示不显著(p=0.12)。

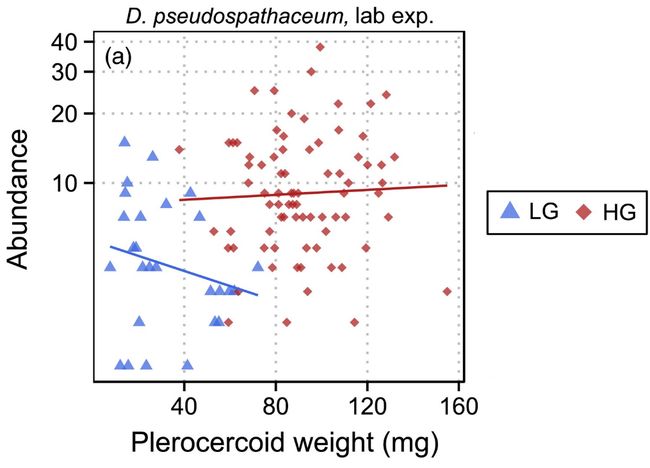
原文图4a部分，展示了在实验室环境中，D. pseudospathaceum丰度与S. solidus重量的关系图。由于广义线性模型(这里是负二项回归)难以绘制，因此仅在作图时改用简单线性回归描述变量间的趋势，但正文还是以负二项回归的结果报告为准。作者在文中还提到，对于该图中观察到的与广义线性模型结果存在冲突的LG组的负相关趋势，可能是简单线性回归难以处理过离散的数据而导致的误报。

R包mvabund的广义线性模型运行示例

以负二项回归为例

R语言中，基础包函数glm()可直接拟合广义线性模型，它提供了对泊松、二项式等多种分布形式的响应变量的分析。此外还有很多其它R包能实现更特定的需求，例如MASS包的glm.nb()可执行负二项回归、loglm()可执行对数线性回归，biglm包bigglm()为大数据集的广义线性模型拟合提供了更灵活的方法。不再多说，实际使用时参考文献中的方法描述以及自己数据集的特点进行选择即可。

恰好上文列举的Benesh和Kalbe(2016)的研究数据，作者有在附件中提供。因此下文就模仿原文过程，仍以广义线性模型的常见子类，负二项回归为例，展示R语言操作。

根据原文中的方法描述，使用R包mvabund中的负二项回归构建广义线性模型，并基于9999次自举估计显著性。下文模仿类似的过程运行一遍，但是在步骤和参数设置上有所更改或增减，因为文中没提到很多运行细节，我很多地方直接使用默认值，因此输出结果和原文统计存在差别，但整体趋势还是差不多的。

原文数据表格，及其相关的描述信息，可在该链接获得：

https://datadryad.org/resource/doi:10.5061/dryad.bq8j8

我也备份到了GitHub中：

https://github.com/lyao222lll/sheng-xin-xiao-bai-yu

数据集概要

数据表格“Lab_exp.csv”，记录了作者试验中的S. solidus试验条件、S. solidus重量、三刺鱼类别、长度、重量、性别等属性特征，以及鱼体中D. pseudospathaceum的丰度等信息。细节详见原文附件描述。

一元回归情形

首先展示最简单的一元回归类型的一个示例，帮助初步了解函数使用和结果解读。

假如只关注某个自变量(如S. solidus试验条件)对响应变量(D. pseudospathaceum丰度)的独立效应，则应用一元回归拟合两个变量的关系。

library(mvabund)

#读取数据

worm  
#首先来看最简单的一元回归示例，假如关注试验条件对寄生虫丰度的独立效应
#拟合广义线性模型，详情 ?manyglm
#这里通过 family 参数指定了负二项回归，其它参数直接使用默认值
fit_glm     family = 'negative.binomial')
#基于 9999 次自举的 Wald 统计量估计 p 值，其它参数直接使用默认值
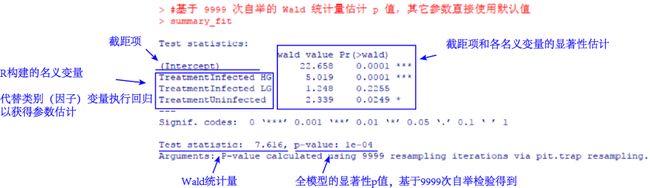
summary_fit summary_fit

结果显示全模型是显著的，表明忽略任何其它因素的影响下，D. pseudospathaceum丰度与S. solidus试验条件有关，即三刺鱼对D. pseudospathaceum侵染的敏感性受到其是否已经被S. solidus侵染以及侵染程度的影响。

有意思的是，在该示例中，自变量是类别变量。通常回归分析要求输入的自变量为数值类型，而在存在类别(或因子)型自变量的线性回归中，由于自变量不是数值变量，此时为了实现回归计算，会使用一系列与因子水平相对应的数值型对照变量来代替类别(或因子)变量，然后再执行拟合。类似的过程在前文“类别型自变量的线性回归”中也有详解。对于本示例，类别变量Treatment(S. solidus试验条件)有4个因子水平：Control、Uninfected、Infected LG和Infected HG，对应于此构建了3个(水平数-1，即4-1=3)名义变量(dummy variables)代替原始的因子，此处显示为TreatmentInfected HG、TreatmentInfected LG、TreatmentUninfected。

#可以通过 contrasts() 查看名义变量的编码过程
contrasts(factor(worm$Treatment))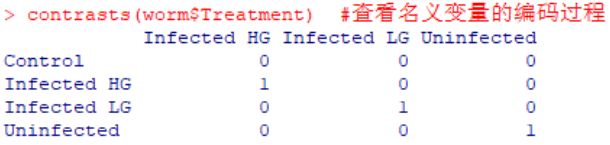

该结果显示了观测值的4个因子水平(4种S. solidus试验条件，4行，Control、Uninfected、Infected LG和Infected HG)和回归式中的3个名义变量(3列，TreatmentInfected HG、TreatmentInfected LG、TreatmentUninfected)的对应关系。例如，当试验条件为Infected HG组时，名义变量TreatmentInfected HG等于1，其余TreatmentInfected LG、TreatmentUninfected都等于0。根据这种对应关系，原始观测值的类别(或因子)变量就被对应的数值替代以执行回归，最终返回对应的参数估计值。

简单一元关系的负二项模型显示，三刺鱼对D. pseudospathaceum侵染的敏感性受到其是否已经被S. solidus侵染以及侵染程度的影响，因此不妨作图观察一下二者独立的关系。

#简单地作图查看试验条件对寄生虫丰度的关系
#感觉蜂群图比抖动点图好看
library(ggplot2)
library(ggbeeswarm)
Diplo_intensity_mean names(Diplo_intensity_mean)  
ggplot(worm, aes(Treatment, log2(Diplo_intensity+1), color = Treatment)) +
geom_beeswarm(cex = 1.5, alpha = 0.6) +
scale_color_manual(values = c('#4C4C4C', '#688A21', '#3F68E1', '#B02121'), 
    limits = c('Control', 'Uninfected', 'Infected LG', 'Infected HG')) +
scale_x_discrete(limits = c('Control', 'Uninfected', 'Infected LG', 'Infected HG')) +
theme(panel.grid = element_blank(), panel.background = element_blank(), 
    axis.line = element_line(color = 'black'), legend.position = 'none') +
geom_point(data = Diplo_intensity_mean, size = 3) +
stat_summary(fun.data = function(x) median_hilow(x, 0.5), 
    geom = 'errorbar', width = 0.2, size = 1) +
labs(x = '')

备注：Control，三刺鱼未暴露于S. solidus，该组用作对照；Uninfected，三刺鱼暴露于S. solidus但未受到侵染；Infected LG，三刺鱼受到低生长速率的S. solidus的侵染；Infected HG，三刺鱼受到高生长速率S. solidus的侵染。

HG组中观察到的D. pseudospathaceum丰度更高，由于HG组代表了三刺鱼受到高生长速率S. solidus的侵染，暗示更高的S. solidus侵染程度也会同时加重D. pseudospathaceum对三刺鱼的二次侵染。

多元回归情形

现在拓展到多个自变量的情况，也就是多元回归形式。

在原文中，作者综合考虑了S. solidus试验条件、三刺鱼体重、性别、类别(这4种变量作为自变量)和D. pseudospathaceum丰度(作为响应变量)关系并进行建模，以比较各因素对D. pseudospathaceum侵染三刺鱼的影响。多元回归中，各自变量之间互为协变量关系对待。

以下根据这个出发点，执行多元形式的负二项回归。此外，本次计算过程中暂且忽略多重共线性的影响。

#原数据中，鱼类别(Fish_family)是用数字代指的，实际上需要修改为因子变量
worm$Fish_family  
#拟合广义线性模型，详情 ?manyglm
#这里通过 family 参数指定了负二项回归，其它参数直接使用默认值
fit_glm     family = 'negative.binomial')
#基于 9999 次自举的 Wald 统计量估计 p 值，其它参数直接使用默认值
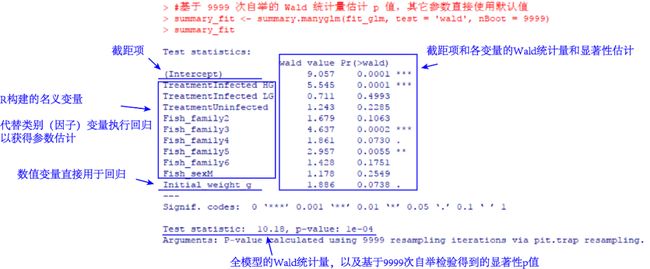
summary_fit summary_fit

原数据集中，S. solidus试验条件、三刺鱼性别、类别都属于类别变量，回归计算时将它们转换为名义变量带入回归。这些变量的转换关系和解读方法和上述一元回归中提到的方法是一致的，不再多说。

三刺鱼体重(Initial_weight_g)是不显著的，表明三刺鱼对D. pseudospathaceum侵染的敏感性与其自身体型无关。

三刺鱼性别的名义变量(Fish_sexM)也是不显著的，表明三刺鱼对D. pseudospathaceum侵染的敏感性与其性别也无关。

S. solidus试验条件和三刺鱼类别的名义变量(TreatmentInfected HG、Fish_family6等)中，存在显著的成分，因此可以认为这两种因素对D. pseudospathaceum侵染三刺鱼产生影响。

再结合全模型是显著的，综合比较分析结果，得到了和作者原文中一致的结论，三刺鱼体重和性别与D. pseudospathaceum的侵染无关，三刺鱼类别和S. solidus试验条件对D. pseudospathaceum侵染的影响显著。再结合上文一元回归中的分析，就不同的S. solidus试验条件而言，HG组中观察到的D. pseudospathaceum丰度更高，表明较高的S. solidus侵染程度也会同时加重D. pseudospathaceum对三刺鱼的二次侵染。

考虑交互效应的情形

如上文所述，已知较高的S. solidus侵染程度也加重D. pseudospathaceum侵染，作者在文中还将S. solidus重量(反映了S. solidus生长)添加在广义线性模型中，评估S. solidus生长对D. pseudospathaceum侵染的敏感性的效应。此外还关注了S. solidus试验条件和S. solidus重量的交互效应。

类似地，继续构建S. solidus试验条件、三刺鱼类别、S. solidus重量和D. pseudospathaceum丰度的负二项回归，并添加S. solidus试验条件和S. solidus重量的交互效应分析。文中作者考虑/不考虑交互效应时的两步多元回归是分开进行的，而这里篇幅起见就直接合在一起作示例了，留意一下。三刺鱼体重和性别已知不显著，就不再考虑在内。此外，本次计算过程中暂且忽略多重共线性的影响。

#拟合广义线性模型，详情 ?manyglm
#这里通过 family 参数指定了负二项回归，其它参数直接使用默认值
#Treatment*Plerocercoid_weight_mg 代表了考虑试验条件和寄生虫重量的交互效应
fit_glm     family = 'negative.binomial')
#基于 9999 次自举的 Wald 统计量估计 p 值，其它参数直接使用默认值
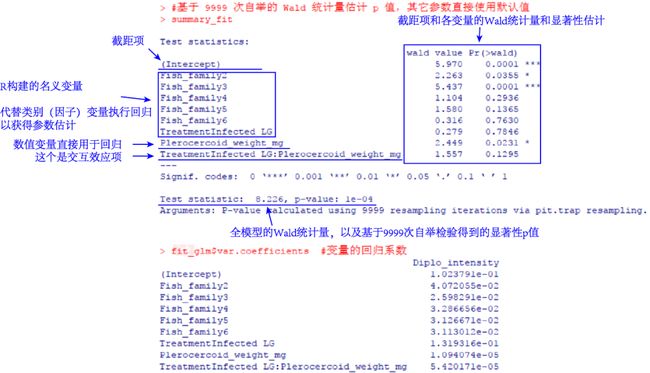
summary_fit summary_fit
#在结果中查看变量的回归系数
#names(fit_glm)
fit_glm$coefficients

类似地，S. solidus试验条件、三刺鱼类别都属于类别变量，回归计算时将它们转换为名义变量带入回归，解读方式参考上文即可。

由于数据集中有关S. solidus重量存在大量的缺失值，计算时默认将这些行对应的数据排除，所以与上文的回归结果相比，缺少了很多信息。例如，缺少了很多S. solidus试验条件的名义变量。尽管如此，仍可以解读关键信息。

S. solidus重量(Plerocercoid_weight_mg)的效应是显著的，且回归系数为正，表明三刺鱼对D. pseudospathaceum侵染的敏感程度也会随S. solidus生长而加重，这个现象和已知较高的S. solidus侵染程度能够加重D. pseudospathaceum侵染的趋势一致，也和原文结论是一致的。

同原文，也没有观察到S. solidus试验条件和S. solidus重量之间存在明显交互效应。

如何评估模型的选择是合适的

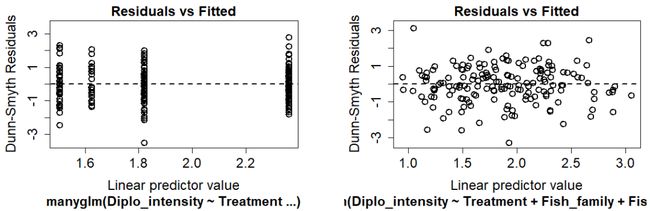
以残差分布图举例评估负二项回归合理性

本文一开始也提到了，尽管广义线性模型覆盖面更广，但也建立在响应变量尽可能满足特定分布的前提下，并需要根据分布特征选择合适的回归子类。若模型选择不合适，同样会使得统计功效较低。那么，怎样评估模型的选择是否是合理的呢？

mvabund包也提供了方法，可使用plot函数生成残差图。如果模型很合适，理论上能观察到点的随机散布。如果看到的是线性或曲线关系或扇形关系等有规则状态，可能意味着均方差关系指定不正确，或者变量之间的假定关系不正确。其它情况，还有可能是离群值的影响。

暂且不考虑离群值的情况，以上述的数据为例作个简单评估，看负二项回归的应用是否是合理的。

#上文 S. solidus 试验条件和 D. pseudospathaceum 丰度的一元关系
fit_glm     family = 'negative.binomial')
plot(fit_glm)
#上文 S. solidus 试验条件、三刺鱼体重、性别、类别和 D. pseudospathaceum 丰度的多元关系
fit_glm     family = 'negative.binomial')
plot(fit_glm)

先后两个回归中都观察到残差的随机散布，表明上文中负二项回归的选择是合理的，统计功效是较强的，结果可信。

作为比较，不妨对上述数据换一种统计模型，例如二项式回归，比较前后结果的差异。

#合理的模型，残差分布均匀(如上文示例，应用的是负二项回归)
mod1     family = 'negative.binomial')
plot(mod1)
#如果是不合理的模型，则残差分布就不均匀(将上文示例中的模型更改为二项式回归)
mod2     family = binomial())
plot(mod2)

通过对比就很清楚了，右图是更改为二项式回归拟合模型后的残差分布，观察到非常偏离的残差值，表明如果将二项式回归应用至这个数据中将会带来非常高的错误。

根据这一点，推广到实际应用中，决定应该使用哪种模型到自己的数据，就是一个很不错的评估方法啦。

     

参考资料

http://environmentalcomputing.net/introduction-to-mvabund/ Robert I. Kabacoff. R语言实战(第二版)(王小宁 刘撷芯 黄俊文 等 译). 人民邮电出版社, 2016. 钱松. 环境与生态统计:R语言的应用(曾思育 译). 高等教育出版社, 2011. Benesh D P, Kalbe M. Experimental parasite community ecology: intraspecific variation in a large tapeworm affects community assembly. Journal of Animal Ecology, 2016, 85(4): 1004-1013. Shaw D J, Dobson A P. Patterns of macroparasite abundance and aggregation in wildlife populations: a quantitative review. Parasitology, 1995. Warton D I, Wright S T, Wang Y, et al. Distance-based multivariate analyses confound location and dispersion effects. Methods in Ecology and Evolution, 2012, 3(1): 89-101. 友情链接

基于降维(特征、成分)的回归方法

R包pls的偏最小二乘(PLS)回归

R包randomForest的随机森林回归模型以及对重要变量的选择

通过Aggregated boosted tree(ABT)评估解释变量的重要性

R语言计算指数回归的方法示例

基于相似或相异度矩阵的多元回归(MRM)及R语言实例

回归中自变量的交互效应及R语言计算示例

多元回归中常见的变量选择方法及其在R中实现

多元线性回归在R中的实现示例

简单线性回归和多项式回归在R中的实现示例

生存分析之R包survival的单变量和多变量Cox回归

多元回归树及重要判别变量识别