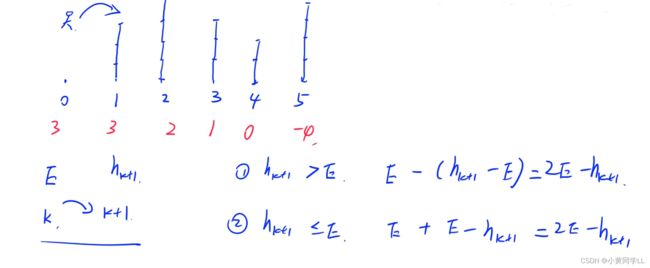蓝桥杯AcWing 题目题解 - 二分与前缀和、差分
目录
AcWing 789. 数的范围 - 整数二分
AcWing 790. 数的三次方根 - 实数二分
AcWing 730. 机器人跳跃问题 - 二分应用
AcWing 1227. 分巧克力
AcWing 795. 前缀和
AcWing 796. 子矩阵的和 - 二维前缀和
AcWing 797. 差分
AcWing 798. 差分矩阵 - 二维差分
整数二分步骤:
1.找一个区间[L,R],使得答案一定在该区间中
2找一个判断条件,使得该判断条件具有二段性,并且答案一定是该二段性的分界点。
3.分析终点M在该判断条件下是否成立,如果成立,考虑答案在哪个区间;如果不成立,考虑答案在哪个区间;
4.如果更新方式写的是R(右) = Mid,则不用做任何处理;如果更新方式写的是L(左)= Mid,则需要在计算Mid时加上1。
AcWing 789. 数的范围 - 整数二分
给定一个按照升序排列的长度为n的整数数组,以及q个查询。
对于每个查询,返回一个元素k的起始位置和终止位置(位置从О开始计数)。如果数组中不存在该元素,则返回-1 -1 。
输入格式
第一行包含整数n和q,表示数组长度和询问个数。
第二行包含n个整数(均在1~10000范围内),表示完整数组。接下来q行,每行包含一个整数k,表示一个询问元素。
1≤q≤10000 1≤k ≤10000 输入样例: 输出样例: 记忆:写完模板后看案例分析始末下标,当 l (左)= mid 时必须mid+1 给定一个浮点数n,求它的三次方根。 输入样例: 输出样例: 来源:今日头条2019,笔试题 输入样例1: 输出样例1: 输入样例2: 输出样例2: 输入样例3: 输出样例3: 思路: 如例一高度 3 4 3 2 4 可以发现通过计算 E=2E-H(k+1),那么只需要将数组所有值带入公式,找到刚好大于0的E即可; 总结: 当题目求“至少”、“至多”,且具有二段性or单调性时,可以考虑二分 (二段性:以某个值为临界,这个值一边的都满足要求,另一边都不满足) 来源:第八届蓝桥杯省赛C++A/B组,第八届蓝桥杯省赛JAVAA/B组 输入样例: 输出样例: 具有单调性与二段性,用二分! 输入一个长度为n的整数序列。 输入样例: 输出样例: 来源:第八届蓝桥杯省赛C++B组,第八届蓝桥杯省赛JAVAB组 思路: 输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数:x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。 输入样例: 输出样例: 用容斥原理推出公式; 首先算出每一个坐标的前缀和s [ i ] [ j ],在前缀和矩阵中再用一次容斥原理 差分思路: 首先给定一个原数组a:a[1], a[2], a[3],,,,,, a[n]; 然后我们构造一个数组b : b[1] ,b[2] , b[3],,,,,, b[i]; 使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i] 即: a[0 ]= 0; b[1] = a[1] - a[0]; b[2] = a[2] - a[1]; b[3] =a [3] - a[2]; ........ b[n] = a[n] - a[n-1]; a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。 首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c; 然后我们打个补丁,b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c; 核心操作:对差分数组b做 b[l] + = c, b[r+1] - = c(时间复杂度为O(1) ) 输入样例: 输出样例: 思路与二维前缀和相似: 操作1、 b[x1][y1] + = c; b[x1,][y2+1] - = c; b[x2+1][y1] - = c; b[x2+1][y2+1] + = c; 操作2、 我们每次让以(i,j)为左上角到以(i,j)为右上角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j],等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作,就成功构建了差分b数组. 说白了,就是让c=a[i][j],把操作1的方法用在一个空数组上,用n*m遍,操作完之后这个数组就是差分数组b[i][j]。 AC代码:
输出格式
共q行,每行包含两个整数,表示所求元素的起始位置和终止位置。如果数组中不存在该元素,则返回-1 -1。
数据范围
16 3
1 2 2 3 3 4
3
4
5
3 4
5 5
-1 -1#includeAcWing 790. 数的三次方根 - 实数二分
输入格式
共一行,包含一个浮点数n。
输出格式
共一行,包含一个浮点数,表示问题的解。注意,结果保留6位小数。
数据范围
-100001000.00
10.000000#includeAcWing 730. 机器人跳跃问题 - 二分应用
5
3 4 3 2 4
4
3
4 4 4
4
3
1 6 4
3
#includeAcWing 1227. 分巧克力
2 10
6 5
5 6
2![]()
#include AcWing 795. 前缀和
接下来再输入m个询问,每个询问输入一对l, r。
对于每个询问,输出原序列中从第 l 个数到第r个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数数列。
接下来m行,每行包含两个整数l和r,表示一个询问的区间范围。
输出格式
共m行,每行输出一个询问的结果。
数据范围
1≤l
5 3
2 1 3 6 4
1 2
1 3
2 4
3
6
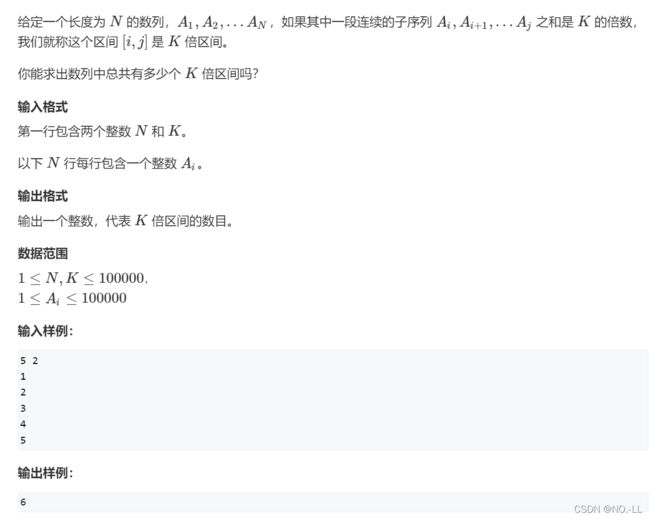
10#includek倍区间
#includeAcWing 796. 子矩阵的和 - 二维前缀和
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n, m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1,y1,x2,y2,表示一组询问。
输出格式
共q行,每行输出一个询问的结果。
数据范围
1≤n, m ≤1000, 1≤q≤200000, 1≤1 ≤2 ≤n,1≤91≤J2≤m,
-1000≤矩阵内元素的值≤1000
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
17
27
21![]()
![]()
#include AcWing 797. 差分
![]()
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1![]()
![]()
#includeAcWing 798. 差分矩阵 - 二维差分
![]()
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
2 3 4 1
4 3 4 1
2 2 2 2![]() 每次对b数组执行以上操作,等价于:
每次对b数组执行以上操作,等价于:for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]+=c; for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
insert(i, j, i, j, a[i][j]); //构建差分数组#include