LeetCode刷题之路:数组二
LeetCode刷题之路:数组二
- 前言
- 一、有序数组的平方
-
- LeetCode第977题:
-
- (1)暴力求解
- (2)双指针
- 二、长度最小的子数组
-
- LeetCode第209题:
-
- (1)暴力求解
- (2)滑动窗口(双指针)
- 三、水果成篮
-
- LeetCode第904题:
-
- (1)暴力求解
- (2)双指针(滑动窗口)
- (3)双指针 + 哈希表
- 四、最小覆盖子串
-
- LeetCode第76题:
- 五、螺旋矩阵Ⅱ
-
- LeetCode第59题:
- 六、螺旋矩阵Ⅱ
-
- LeetCode第54题:
- 总结
-
- (1)数组
- (2)二分查找
- (3)双指针
- (4)模拟
前言
上一偏文章记录了数组算法专题训练的前二分之一的题目,在这篇文章中继续记录后面的内容。
一、有序数组的平方
LeetCode第977题:
(1)暴力求解
暴力求解的思想是先处理数组,将数组的每个元素平方得到更新后的数组,接着将更新后的数组排序。
代码如下:
def sortedSquares(array):
n = len(nums)
for i in range(n):
nums[i] = nums[i] * nums[i]
nums.sort()
return nums
代码非常的简单,直接使用了内置函数sort()。
其实在这里最开始的尝试为自己写了一个快速排序的qsort函数,但是运行后发现超时了,代码如下:
def sortedSquares(array):
n = len(nums)
for i in range(n):
nums[i] = nums[i] * nums[i]
def qsort(array):
if len(array) < 2:
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i <= pivot]
greater = [i for i in array[1:] if i > pivot]
return qsort(less) + [pivot] + qsort(greater)
return qsort(nums)
后面网上查找资料发现,python的内置排序函数采用的是Timesort算法,稳定且快熟,是最好的排序算法之一,但是目前还没有仔细查看其中的原理。
(2)双指针
双指针的思路为构造左右两个指针,分别由左右两端遍历,比较两个指针所指元素平方的大小,并构建一个新的数组存入每次的较大值,这时存入元素的指针移动,为存入的不移动。
这种算法的时间复杂度为O(n),代码如下:
def sortedSquares(array):
n = len(nums)
Left_Index = 0
Right_Index = n - 1
result = n * [0]
for i in range(n):
if nums[Right_Index] * nums[Right_Index] >= nums[Left_Index] * nums[Left_Index]:
result[n - 1 - i] = nums[Right_Index] * nums[Right_Index]
Right_Index = Right_Index - 1
else:
result[n - 1 - i] = nums[Left_Index] * nums[Left_Index]
Left_Index = Left_Index + 1
return result
二、长度最小的子数组
LeetCode第209题:
(1)暴力求解
两层for循环,求解每个元素开头的最小字符串,选择最小值,代码如下:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
# 暴力求解思想,两次for循环
n = len(nums)
sum = 0
final = float('inf')
for i in range(n):
sum = 0
k = 0
for j in range(i, n):
sum = sum + nums[j]
k = k + 1
if sum >= target:
final = min(final, k)
break
if final == float('inf'):
return 0
else:
return final
时间复杂度为O(n**2),最终结果超时了。
(2)滑动窗口(双指针)
移动窗口的思路与双指针类似,而比较大的区别在于滑动窗口更加关注窗口内的元素。这一题的思路就是用两个指针分别指代窗口的左右两端,结束端的遍历依靠for循环,在for循环内累加元素得到sum,左端口的值改变依靠for循环内的while循环,判断条件为sum > target,在满足此条件的基础上,不断移动左端口并调整sum和res(记录窗口内的元素个数)的值,直到条件不断满足,时间复杂度为O(n)。代码如下:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
i = 0 # 记录左端窗口
sum = 0
res = float('inf') # 无限大
for j in range(len(nums)): # 遍历右端窗口
sum = sum + nums[j]
while(sum >= target): # 当窗口内的值满足要求时(即大于target),移动左端窗口,直到不满足
res = min(res, j - i + 1) # 实时更新res的值
sum = sum - nums[i]
i = i + 1
return 0 if res == float('inf') else res
三、水果成篮
LeetCode第904题:
(1)暴力求解
直接采用暴力求解会超时,按照测试样例修改代码后勉强通过:
def totalFruit(self, fruits: List[int]) -> int:
# 问题简化:包含两个不同元素的最长连续串
# 暴力求解-两层for循环,迭代更新从各个位置开始的最大两个元素长度:
n = len(fruits)
res = 2
num = len(set(fruits))
if num < 3:
return n
elif n > 90000:
d_fruit = set()
for i in range(n):
d_fruit.update({fruits[i]})
if len(d_fruit) > 2:
return i
else:
for i in range(n):
Two_fruit = []
j = i
while j < n: # j < n ,防止溢出
if fruits[j] not in Two_fruit:
Two_fruit.append(fruits[j])
if len(Two_fruit) > 2: # 需要考虑只有一棵树的情况
break
else:
j = j + 1
res = max(res, j - i)
return res
这时非常笨的方法,不建议采用,试试能否骗过测试代码而已。
(2)双指针(滑动窗口)
准确来说也不能算做滑动窗口了,左侧窗口并不是完全顺位滑动,中间存在跳动的情况,所以可能双指针更为合适。代码如下:
def totalFruit(fruits):
# 问题简化:包含两个不同元素的最长连续串
# 双指针遍历一次数组返回最大值
n = len(fruits)
Baskets = [] # 建立果篮,存放水果
res = 0
Left_Index = 0 # 慢指针,复制在不满足条件是更新
for Right_Index in range(n): # 快指针,负责向前遍历
if fruits[Right_Index] not in Baskets:
Baskets.append(fruits[Right_Index]) # 当右窗口元素是新元素时,加入果篮
if len(Baskets) < 3:
# res = max(res, Right_Index - Left_Index + 1)
res = max(res, Right_Index - Left_Index + 1) # 不能直接 + 1
# print([Right_Index, Left_Index, res,'a'], Baskets)
else:
# Baskets.pop(0) 不一定是去掉第一个元素,而是去掉不是新元素或前面一个元素的元素
Baskets = [fruits[Right_Index - 1], fruits[Right_Index]]
Left_Index = Right_Index - 1
while fruits[Left_Index] == fruits[Left_Index - 1] and Left_Index > 0:
Left_Index = Left_Index - 1
res = max(res, Right_Index - Left_Index + 1)
# print([Right_Index, Left_Index, res,'b'], Baskets)
else:
res = max(res, Right_Index - Left_Index + 1) # 不能直接 + 1
# print([Right_Index, Left_Index, res,'c'], Baskets)
return res
大体思想为,快指针使用for循环遍历,慢指针通过条件(窗口内超过两个元素时,即果篮数量大于2时)向前遍历,而不同于一般的做法,这里慢指针的每次遍历是直接跳转到快指针指向的前一个元素然后再向左查找到最后一个相同元素,这一题写了挺久的,主要问题在于代码中间的细节很多:
1、由于最终返回的结果一致存在判断,所以在任何时候都不能直接 + 1,而是需要用max来判断;
2、果篮的删除不能直接删除最左侧元素,可能删除的是中间的元素,这个时候直接覆盖数组值更加方便。
(3)双指针 + 哈希表
使用哈希表数据结构在这里表示更为清晰:
def totalFruit(self, fruits: List[int]) -> int:
# 问题简化:包含两个不同元素的最长连续串
# 双指针遍历一次数组返回最大值
# 哈希表简化问题
cnt = Counter() # 计数器,dict类型,key为元素,value为出现的次数
left = 0
ans = 0
for right, num in enumerate(fruits):
cnt[num] = cnt[num] + 1
while len(cnt) > 2:
cnt[fruits[left]] = cnt[fruits[left]] - 1
if cnt[fruits[left]] == 0:
cnt.pop(fruits[left])
left = left + 1
ans = max(ans, right - left + 1)
return ans
四、最小覆盖子串
LeetCode第76题:
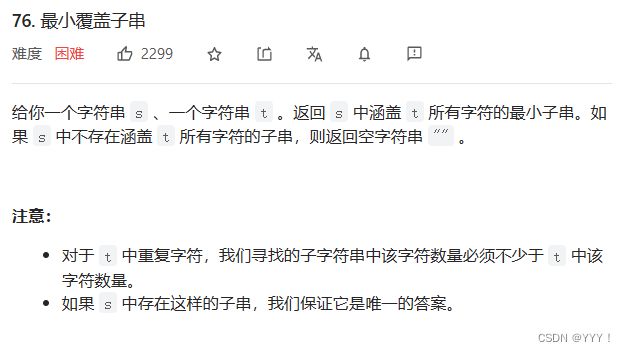
这一题仍然是滑动窗口的思想,右端窗口先动,这时左端窗口不动,当窗口内部包含目标字符串时,左端窗口动而右端不动,当不在包括所有字符串是,右端再动如此循环。这题唯一增加难度的点在于对是否包含字符串的判断,也是运行时间产生差异的最主要原因。代码如下:
class Solution:
def minWindow(self, s: str, t: str) -> str:
def check_0(cnt_t):
n = 0
for k, v in cnt_t.items():
if v <= 0:
n += 1
if len(cnt_t) == n:
return True
else:
return False
cnt_t = Counter(t)
left = 0
ans = ''
res = [float("inf"),-2,-2] # 记录长度,left,right
for right, i in enumerate(s):
if i in cnt_t:
cnt_t[i] -= 1
# if check_0(cnt_t):
while check_0(cnt_t) and left <= right:
if res[0] > right - left + 1: # 找到更合适的取值时
res = [right - left + 1, left, right]
if s[left] in cnt_t:
cnt_t[s[left]] += 1
left += 1
if res[0] == float("inf"):
return ""
else:
return s[res[1]: res[2] + 1]

可以看到运行时间还是过长,而代码主要可以由两个方面优化,第一就是前面说的cherk_0函数,判断窗口空间是否包含字符串,第二就是按照答案中的思路,去掉所有非目标元素的字符串,目前笔者的思路是用0表示其他元素,只留下需要的元素,而在窗口滑动的过程中改变移动形式,将滑动改变为跳动,即当遇到连续的0时,直接跳转到非0的元素,这样减少包含关系的判断次数,目前笔者还没做优化,后续再更新这个题目。
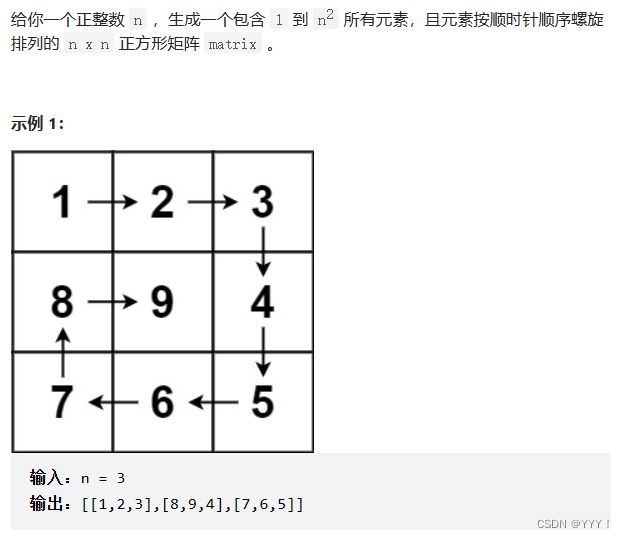
五、螺旋矩阵Ⅱ
LeetCode第59题:
这种题目属于模拟题目,这里模拟的时螺旋,整体感觉难点在于处理边界判断的问题,代码如下:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
top = 0
bottom = n - 1
left = 0
right = n - 1
mat = [[0] * n for _ in range(n)]
num = 1
while num <= n**2:
for j in range(left, right + 1):
mat[top][j] = num
num = num + 1
top = top + 1
for j in range(top, bottom + 1):
mat[j][right] = num
num = num + 1
right = right - 1
for j in range(right, left - 1, -1):
mat[bottom][j] = num
num = num + 1
bottom = bottom - 1
for j in range(bottom,top - 1, -1):
mat[j][left] = num
num = num + 1
left = left + 1
return mat
六、螺旋矩阵Ⅱ
LeetCode第54题:
这个题目与上面一题类似,可以用相同的方法,直接理解为一条直线,然后需要调整上下左右边界。需要注意的是num的越界问题,对这个问题有两种解决方式,见代码中的备注,代码如下:
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m = len(matrix) # m行
n = len(matrix[0]) # n列
left = 0
top = 0
right = n - 1
bottom = m - 1
nums = m * n
mat = [0] * (nums + max(m, n))
# 由于循环不是直接跳出,num的值一致增大,这样使得mat的索引可能会越界。
# 这种情况要么添加判断条件,会牺牲时间节省空间;要
# 么添加mat空间,最后返回需要的部分。
# 这里的做法时增加空间,max(m, n)为证明,感觉是这样
num = 0
while num < nums:
for j in range(left, right + 1):
mat[num] = matrix[top][j]
num = num + 1
top = top + 1
for j in range(top, bottom + 1):
mat[num] = matrix[j][right]
num = num + 1
right = right - 1
for j in range(right, left - 1, -1):
mat[num] = matrix[bottom][j]
num = num + 1
bottom = bottom - 1
for j in range(bottom,top - 1, -1):
mat[num] = matrix[j][left]
num = num + 1
left = left + 1
return mat[0:nums]
总结
数组的部分需要掌握的知识大概就在以上的题目中了,现在整体回顾一下:
(1)数组
数组需要注意的是其储存空间的连续性,数组的查找非常迅速,但是删减比较慢,这一点与链表恰好相反,元素不能直接删除而是进行覆盖。
(2)二分查找
二分查找的思想很重要,一般有两种形式,左闭右闭和左闭右开,一般笔者喜欢采用左闭右闭的形式。需要注意的就是while的判断中是left <= right,然后在num更新过程中,直接替换为left的右侧元素,或者right的左侧元素。相比于暴力求解O(n)的复杂度,二分查找的时间复杂度只有O(logn),二分查找的运用需要数据的顺序排列。
(3)双指针
双指针是非常有用的概念,能够进行代码的优化,其实思想也非常的简单,一快一慢的两个指针,二者的遍历条件不一样,且快指针的遍历不会被慢指针影响,同样慢指针做出的修改操作不会影响快指针的后续判断(可影响已经判断的部分)。滑动窗口实际上运用的就是双指针的思想,不过关注点由指针所指向的两个元素变为了两个指针之间的元素,即窗口间的元素。
(4)模拟
模拟的题目就是螺旋矩阵的两个题目,对于这两个题目主要是需要找到遍历的形式与边界条件的判断。
以上便是数组的全部内容,下面我们继续探索链表。