旅行售货员问题及其近似算法（NPC问题）

一、基本介绍

设有n个城镇，已知每两个城镇之间的距离，一个售货员从某一城镇出发巡回售货，问这个售货员应如何选择路线，能使每个城镇经过一次且仅一次，最后返回到出发地，而使总的费用最少？这就是旅行售货员问题。

哈密顿（Hamilton）圈：给定一个图G(V，E)，如果G中的圈C恰好经过每一个顶点仅一次，则称该圈C为哈密顿圈。

旅行售货员问题就是在一个赋权完全图中找一个具有最小权哈密顿圈，即找到一个圈经过每个点仅一次，并且总权值最小，我们称这种圈为最优哈密顿圈。而哈密顿圈问题也是NPC问题的一种，故旅行售货员也是NP完全问题。

二、问题解法

旅行售货员问题可以对以下四种方法进行讨论：

2.1 枚举法（穷举法）

设图G=(V,E)是一个带权图，权值代表两个城镇间的所需费用，旅行售货员问题要找出费用最小的周游路线。
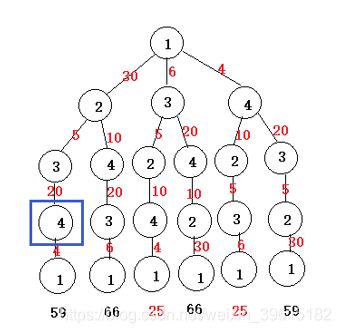
旅行售货员问题的解空间可以组织成一棵树，从树的根节点到任一叶子节点的路径，如图。

假设有n个城市，从第一个城市走到第二个城市有n-1种走法，第二个到第三个有n-2种走法，… ，因而共有(n-1)!种解法。如下图，n=4时，第0层到第1层—3种走法，第1层到第2层—2种走法，第2层到第3层—1种走法，(4-1)!=3!=6。

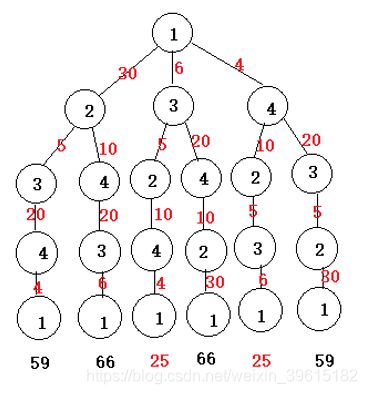
若考虑顶点V1V2…VnV1和V1Vn…V2V1是同一条回路（经过顶点和边相同），如下图，则剩下不同的回路还有一半，即(n-1)!/2。

为了比较权的大小，对每条哈密顿回路需要做n次加法，总和为[(n-1)!/2]×n，时间复杂度为O(n!)，这种级别计算量显然不可取，我们需要的目标复杂度是O(n^k)，即多项式。

2.2 回溯法

旅行售货员问题的解空间是一棵排列树。
回溯算法backtrack描述如下(深度优先搜索—假设先序)：
1、当i=n时，当前扩展结点是排列树叶子结点的父结点
①检测图G是否存在一条从顶点x[n-1]到顶点x[n]的边和一条从顶点x[n]到顶点x[1]的边。
②如果这两条边都存在,则找到一条旅行员售货回路。
③此时,算法还需要判断这条回路的总权值是否优于已找到的当前最优的路线bestc
④如果是,则必须更新当前最优值bestc和当前最优解

2、当i ①图G中存在从顶点x[i-1]到顶点x[i]的边时，x[1:i]构成图x[1:i]的总权值小于当前最优值时算法进入树的第i层
②否则将剪去相应的子树。

backtrack最坏情况下，需要每条路都走一遍，即(n-1)!种走法，时间复杂度O(n!)

2.3 分支限界法

分支限界法常以广度优先或最大效益优先的方式搜索问题的解空间树。
优先队列式分支限界法：按优先级选取优先级最高的下一个结点为当前的扩展结点，权值越小优先级越高。

算法描述:
①准备工作：建立小根堆，用于存储活动节点。计算每个顶点的最小出边，若存在某个顶点没有出边，则算法终止。初始化树根(顶点1)为第一个活动节点。
②判断节点是否是叶结点的父节点：是的话,则检查是否一定有最低耗费，若是加入小根堆不是叶结点的父节点，则生成子节点，并判断子节点是否有可能取得最低耗费，若可能则加入小根堆。
③取出下一个节点作为活动节点，若该节点已经是叶结点，返回当前最低耗费值，即为最优旅行。若不是叶结点则循环2、3步。

分支限界法扩展步骤：



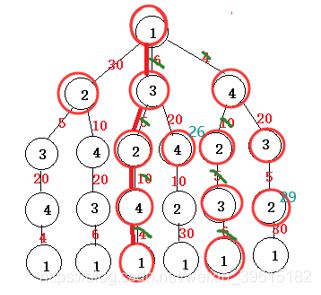
一个26，一个29均大于25，故(1,3,2,4,1)即为最优路线
分支限界法时间复杂度：O(n²×2ⁿ)
其中搜索O(2ⁿ)，对每个结点计算O(n²)

2.4 旅行售货员问题近似算法

该算法抽象出旅行售货员问题具有一些特殊性质。如费用函数c往往具有三角不等式性质，即对任意3个顶点u，v，w有c(u,w)<=c(u,v)+c(v,w)。在该条件下，且算法找出的旅行售货员回路的费用不会超过最优费用的2倍（三角形性质），旅行售货员问题仍为NP完全问题。

算法描述：
①选择图G的任意一点作为根顶点（此处选顶点a）
②用Prim算法找出带权图G以a为根的最小生成树T
③先序遍历最小生成树得到顶点表L
④将a加到表L的末尾，并将完全遍历后的顶点集合写出，得到一条旅行回路H={abchdefga}

采用朴素Prim算法时间复杂度为O(n^2)，若继续用二叉队优化Prim算法可达到O(elog(v))。其中e为边，v为结点。

三、总结

我们可以得到四个算法的时间复杂度
1、枚举法 O(n!)
2、回溯法 O(n!)
3、分类限界法 O(2ⁿ)
4、NP近似算法（旅行者问题近似算法） O(n²) √

故该旅行售货员近似算法最好。