栈与递归（Hanoi塔问题）

  今天上午上课时，再看了下Hanoi塔的问题，其中对递归的分析，让自己对递归调用有了更深一步地理解，把书上的代码实现一下，然后分析其递归工作栈的状态，理解了以后，会让自己受益颇多。学习，不能只看着别人是怎么写的，自己就照着写，这是非常不对的，你要分析别人为什么这样写，你要懂得的是思路，而不仅仅是答案。

 1 #include<stdio.h>

 2 static int c;

 3 void hanoi(int n,char x,char y,char z)

 4 {

 5     if(n==1)//将编号为1的圆盘从x移到z

 6         printf("%d step: Move disk %d from %c to %c\n",++c,n,x,z);

 7     else

 8     {

 9         hanoi(n-1,x,z,y);//将x上编号为1至n-1的圆盘移到y,z作辅助塔

10         printf("%d step: Move disk %d from %c to %c\n",++c,n,x,z);

11          //将编号为n的圆盘从x移到z

12         hanoi(n-1,y,x,z);//将y上编号为1至n-1的圆盘移到z,x做辅助塔

13     }    

14 }

15 int main()

16 {

17     int n;

18     printf("请输入hanoi塔的阶数：\n");

19     scanf("%d",&n);

20     hanoi(n,'A','B','C');    

21 }

运行结果：

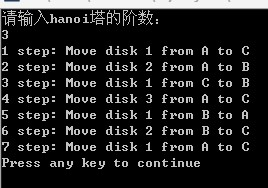
分析：

   假设n=3,递归第一层的状态为（返址：0,3,A,B,C）执行到第9行语句时，递归调用第二层（返址：6,2,A,C,B） 此时栈的状态时在第一层之上，继续递归调用又回到第9行语句，递归调用第三层（返址：6,1,A,B,C）此时栈的状态时在第二层之上，继续递归调用，这时n=1，所以会有第一步的输出，A->C.输出后，跳到第14行语句也就意味着递归的第三层函数调用结束，返回到递归调用的第二层（返址：6,2,A,C,B）继续向下执行到第10行代码，这是第二步输出，A->B.

然后执行到第12行代码，这是又遇到递归函数，前面还有两层递归调用，所以这是递归调用第三层（返址：8,1,c,a,b）,执行递归调用，此时n=1,所以第三步输出，C->B,执行完后跳到14行代码，以为着第二层函数调用结束，返回到第一层（返址：0,3,A,B,C）,第一层的递归调用执行第10行代码，就会用第四步输出，A->C,继续执行到第12行代码，又遇到递归调用，此时状态为递归调用第二层（返址：8,2,B,A,C）,继续执行，会到第9行代码此时又遇到递归调用，递归调用第三层（6,1,B,C,A）,继续执行此递归调用,到第5行代码，此时n=1所以输出第五步：B->A.执行完后到第14行代码，这是意味着第三层递归调用结束，回到第二层递归调用，接着执行第10行代码,这是第六步输出：B->C. 执行完后到12行代码，又遇到递归调用（返址：8,1,A,B,C）,递归调用执行到第5行代码，满足条件，输出第七步：A->C。回到第二层递归调用，第二层递归调用又执行到第14行代码，这意味递归调用结束，返回主函数。

找下规律，从运行的效果图可以看出：

根据圆盘的数量确定柱子的排放顺序：若n为偶数，按顺时针方向依次摆放 A B C；看第2块，从A->B,B->C

若n为奇数，按顺时针方向依次摆放 A C B。看第一块，A->C,C->B,B->A,A->C.第3块：A->C

呵呵，百度的时候，看到还有这样的智力游戏，这下我碰到了应该会玩了哈。。。

总结：自己分析得不怎么好，当自己去想，自己去做时，会发现书上写得有多好，自己写的水平有多差了。hanoi塔问题，找到简单的办法解决看似复杂的问题。不过递归调用也不简单，虽然只有那么几行代码，可是分析起来是会死掉一些脑细胞的。。。嘻嘻。。。