国科大UCAS大气物理期末复习笔记/大气物理基础入门

2021秋季学期，主讲教师为卞建春研究员，其中郄秀书研究员介绍了大气电学相关。
考虑到大气物理学基础的在日后研究中十分重要，故稍作整理。
主要参考为课程PPT、作业、大纲
书籍： Atmospheric Science John M. Wallace & Peter V. Hobbs (2006)
Atmospheric chemistry and Physics (air pollution & climate change), John H. Seinfield and Spyros N. Pandis(2006)
*观前提醒：本文仅为在校研一学生期末复习笔记，内容为相关领域最最基础浅显的理论，并不涉及前沿讨论。
作者本人水平即为有限，且会着重介绍自己认为重要、感兴趣的难点重点。有出错之处还请多包涵指正。
包含内容：大气热力学、云降水物理、气溶胶与云化学、大气辐射学基础
由于大气电学与边界层内容在大气物理学中较为独立且介绍较浅显，本文不涉及（并非不重要，实际上，每一章的内容都十分重要高深。）

1、引言&简介

大气物理学是大气科学学科的核心课程之一，它与研究大尺度范围内天气现象、季风环流、大气动力学不同，它寻求从物理原理来解释大气中发生的各种时间与空间尺度的现象。大气物理学可以广泛地认为包括所有大气现象。流体力学、热力学、电磁学、晶体学。
领域：大气辐射、气溶胶物理学、云物理学、大气电学、大气边界层物理学、小尺度大气动力学。
换句话说，天气学原理和动力气象学往往集中于大尺度天气的运动状态，而大气物理学则研究大气本身以及大气中其他成分与大气间的各种物理过程，大气物理学的研究可以增强我们对于大气本身的认识，从而加强对于天气、气候预测的水平。
这份笔记主要涉及大气热力学、云微物理学、气溶胶微物理、大气辐射学的一些最基本的理论，便于为后续研究打下基础。

2、大气热力学

顾名思义，研究大气热力过程的一章。
热力学是经典物理学理论的基石之一，它对我们理解各种尺度的大气现象（从云微物理到大尺度环流）都起着重要作用。
在此章节，会介绍热力学基本思想与关系，并将其应用于一些简单重要的大气过程中。
此章节涉及的一些相关概念极为重要，可以说贯穿整个学科中。
本章基本框架如下图：

2.1 热力学基本概念与定律
首先我们要明确自己的研究对象与对象特征及其描述。
在物理学中，常将研究对象称为“系统”，用状态描述系统的化学物理综合特征，用状态函数对系统物理量进行描述与量化。简单地说，我们可以将热力学概括为：定性与定量描述系统热力学状态改变的过程与途径学科。
系统状态的改变必然涉及与外界的物质能量交换，诚然，并不是所有系统都涉及物质能量交换过程，据此，可将系统分为：孤立系统、封闭系统、开放系统。
而在大气热力学中，毫无疑问，我们研究的系统变为地球大气，不仅包括大尺度范围的大气，还包括局地范围的空气块。根据上述定义，大尺度大气毫无提问与外界环境存在物质与能量的交换，属于开放系统。但需要指出的是，在实际研究中，为了简化问题。我们采用一些理想化模型，也会出现将气块视作孤立、封闭系统的情况。
热力学定律与相关基本概念见下图：

图3.1 状态与状态函数

图3.2 热力学基本过程

图3.3 热力学基本定律

2.2 理想气体状态方程
实验表明，任何物质的体积、温度、压力都可以用某种状态方程来表示。而所有的气体都遵循近似相同的状态方程，即理想气体方程。它是描述理想气体处于平衡态时，压强、体积、质量、温度间关系的状态方程。
pV=mRT
p为压力，V体积，m为质量，T为热力学温度（K），R为气体常数，其大小依赖于不同对象。
理想气体是一种假想的气体，需要满足：1、气体分子本身没有体积 2、分子间不存在相互作用力，本身并不存在。
然而对于实际地球大气而言，分子间平均距离比较大，分子间作用力比较小，分子自身体积与气体体积相比微不足道，平均自由程远大于分子大小，（满足高温、低压条件），可近似看成理想气体。
理想气体状态方程中的R因气体不同而有所改变，为此，定义普适气体常数R*=R/M（M为摩尔质量）= 8.3145 J K–1 mol–1
则理想气体状态方程转换为：
ρV = nR*T
*此方程可用在大气探测中计算大气密度
然而，实际大气并非理想气体，为了更好描述地球大气宏观物理性质，荷兰物理学家Van der Waals对理想气体状态方程提出了改进，考虑了分子间作用力和分子大小。
Van der Waals气体模型的假设为：
气体微粒为硬球，有一个确定的体积，不能超极限挤压， 两个微粒近距离相互作用，独自占有球形体积。
由于每个粒子都占有一定的体积，故其运动范围就不是整个容器的体积，而要小一些。因而理想气体的体积被高估了，对于实际气体需要缩减。实际气体的体积（VR）等于容器的体积（即理想气体的体积，V）减去体积订正因子b：VR = V -nb.
由于气体微粒之间存在相互作用力（ 分子间作用力），在表面，由于表面之外不存在气体，分子间作用力无法平衡，因此向内存在一个拉力，因此，对于实际气体，微粒展现的气压小于理想气体的气压。
气压减少量正比于整体微粒数密度的平方，从而得到真实气体的气压为
Pi = Pr + an²/V ²
则：(P+an²/V²)(V-nb) = nRT
Van der Waals气体模型在低压情形下，与理想气体模型相差较小，而在高压条件下模拟结果差别较大。
2.3 大气水汽
在一定条件下向系统提供热量，它可能产生相的变化，而不是温度的变化。在这种情况下，内能的增加完全与分子间力存在时分子构型的改变有关，而不是分子动能的增加(因此也就是系统温度的增加)。也就是所谓相变的过程。由于相变产生/吸收的热量称为潜热（latent heat），与之对应，由于温度变化引起的热量改变称作感热（sensible heat）。
在大气中，水的相变过程对是大气的重要热力过程之一，水汽含量对大气热力状态与其他过程有着重要影响。因此，在研究大气的热力过程前，我们首先要了解大气中的水汽含量表示与相应的概念。
饱和水汽压（平衡水汽压）：如下图，温度为T的纯水开始蒸发，蒸发过程中，盒中气态水分子数逐渐增加，致水汽压增加。
同时，气态水又会凝结返回液态水面，当水汽的凝结速率等于蒸发速率时，水与空气间的压强达到平衡，此时对应的水汽压强es称为温度T时纯水面上的饱和水汽压，准确叫法应为“平衡水汽压”。即达到动态平衡。

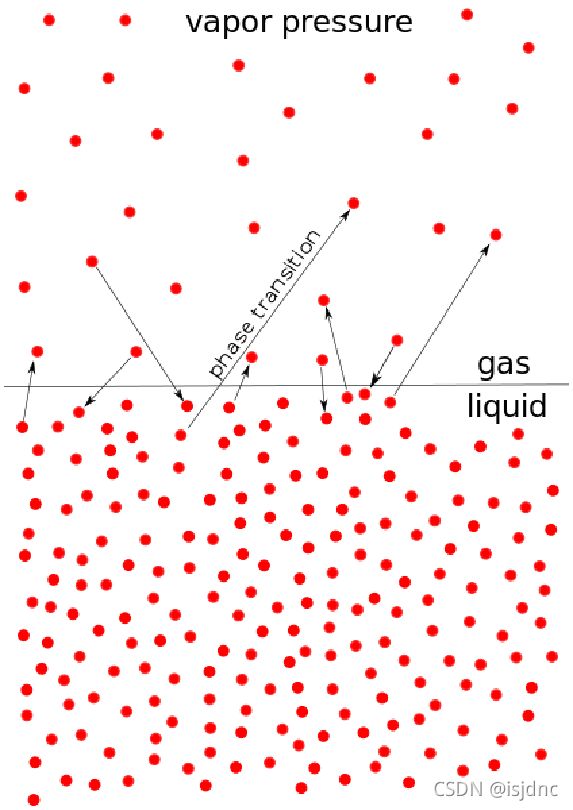
平衡水汽压随温度非线性变化，满足克劳修斯-克拉伯龙（Clausius-Clapeyron）方程。

es饱和水汽压、 Lv蒸发比潜热（温度T的函数）、Rv水汽气体常数。
相对应的，如果把温度T的纯水面换成度为T的冰面，当返回率等于蒸发率时的水汽压esi称为温度为T时的冰面饱和水汽压。此时再引入两个概念：
露点（dew）Td：是在维持空气气压不变的情况下，把空气冷却到相对于纯水面（平面）来说达到饱和时的温度。
霜点（frost）Tf：是不改变气压条件下，把空气冷却到相对于纯冰面（平面）为饱和时的温度。
esi与es的相对关系如下图，不难看出在同一时刻，水分子从水面或冰面蒸发的速率都随温度的升高而增大，因此esi与es是温度T的函数，也受液（或冰）面形状影响。
而在任何温度下，冰的蒸发率都小于水的蒸发率，因此es(T) > esi(T)。

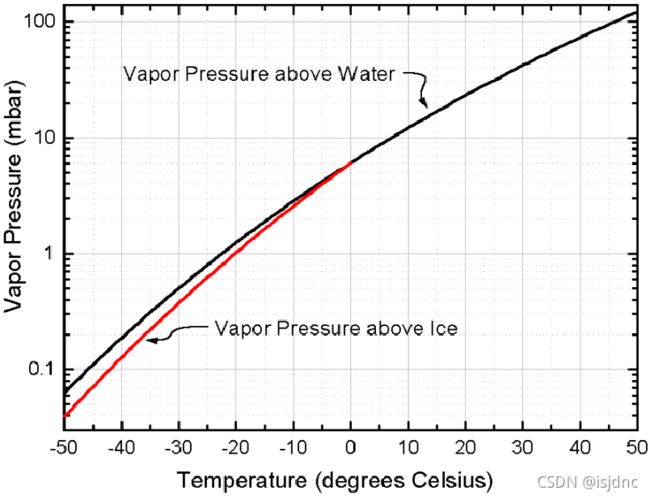
根据饱和水汽压概念，我们可以引入几个与水汽含量相关概念。
相对湿度：空气相对湿度（液面）定义为空气中水汽分压与空气温度饱和水汽压（液面）之比。

比湿：单位质量空气（干空气+水汽，kg）中水汽质量mv（g）所占的比例，称作比湿q。

混合比：单位质量干空气（kg）中水汽质量mv（g）所占的比例，称作混合比。
大气化学中，我们常用体积混合比的概念来描述气体成分在大气中的含量。即某成分与空气数浓度之比，亦即分压与总压之比（根据道尔顿分压定律）。
上述的几个概念非常重要，对它们的理解将有利于我们介绍与描述大气的绝热过程。

2.4 绝热过程与大气稳定度
绝热过程，顾名思义，是指系统与环境间无热量交换的过程。在这个过程中，它的物理状态（如温度、体积、气压）发生变化，其热量不变。
再讨论之前，我认为应当先解答一个问题：为什么要研究大气的绝热过程？或者说，研究大气的绝热过程有什么意义？这无疑是一种理想化的模型，实际大气无疑会违反我们的假设，简单理想化的模型有助于理解大气的垂直运动与垂直结构过程。
在绝热过程中，我们研究的对象是一个理想的小气团，这个理想的小气团需要满足：1、孤立系统 2、准静力平衡 3、其动能相对总体能量可以忽略。
通过与实际情况与理想状况的对比，我们也可以得出实际大气的物理状态（稳定度）。
也可以这么解释：热量的交换需要温差（在大气中），而符合绝热过程的大气沿着等熵面上升（称之为中性），如果大气不符合绝热过程（涉及热交换），那么可以我们根据大气当前的热力状态，分析大气的垂直运动与结构。

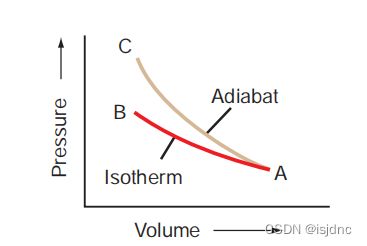
图3.4 绝热过程（AC）与等温过程（AB）
在搜索过程中发现了很有的博客，底下评论对于绝热的讨论也可以帮助我们理解：绝热递减率推导评论与回复
下面开始讨论大气的绝热过程、
干绝热过程
干绝热过程：不饱和气块的绝热过程。
对于干绝热过程,其能量变化只涉及两方面：机械能平衡与热量平衡。即重力做功与温度变化，根据热力学第一定律，重力做功量＝温度变化引起的热量变化，即有：

Cp为,定压比热容，α为比容，可以理解为单位质量的气块所占体积。
根据假设，气块满足准静力平衡，于是：

联立两式，干绝热温度递减率为
-dT/dz=-g/Cp≈9.8℃/km
饱和绝热与假绝热过程
上面讲到的干绝热过程，研究的对象是干空气块，那么对于湿空气块，结果又如何呢？
我们知道，水汽对于热平衡的影响来自于它自身相变而释放的潜热。一个干气块上升，温度以干绝热递减率降低，直到气块达到水汽饱和为止（上升→温度降低→饱和水汽压降低）。
随后，水汽凝结发生相变，释放出潜热，气块温度递减率变小。如果全部凝成物存留在上升气块内，且释放潜热没有流出该气块，则该过程可视为绝热的（可逆的），即饱和绝热过程。但是，如果全部凝成物都掉出气块，则这该过程不可逆的，是一次假绝热过程。
凝结物掉出所带走的热量可忽略不计，因此饱和绝热递减率与假绝热递减率基本相同。
对于湿绝热过程，根据能量守恒，有：

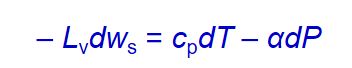
Lv为潜热，dWs 水汽凝结后空气块比湿的变化，有

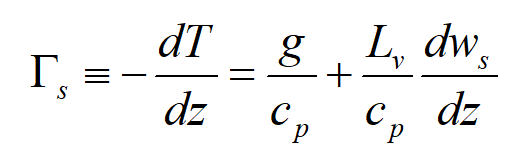
即湿绝热由气块膨胀做功产生的冷却与凝结产生潜热共同作用，不难看出，湿绝热温度递减率通常小于干绝热递减率。
大气静力稳定度
我们前面提到，研究气块的绝热过程，有利于我们了解大气的垂直结构与垂直运动状态，那么，我们又如何利用计算的绝热温度递减率来判断垂直方向上的运动状态呢？这里，我们引入大气静力稳定度的概念。
什么叫做大气的静力稳定度？简单来讲，就是在没有外力的条件下，一个气块仅仅凭借自身的热力状态，气块自发的运动趋势。
在垂直方向上，气块的运动趋势无非两种：上升、下降，在气象学中，上升表示着对流，对应大气条件的不稳定（易发生天气现象），气块下沉，无对流，对应稳定状态（不利于产生天气现象）。
从能量角度也很好理解：气块上升→重力势能增加，内能减少，大气放热→外部环境熵增，不稳定。
气块下沉→重力势能减少，内能增加，大气吸热→外部环境熵减，稳定。
我们都知道“热胀冷缩”，假想的小空气块通常可以看作理想气体，由理想气体状态方程，气体温度越高，其密度越小，气块就会上升。
如何判断气块温度相对于周围环境的大小？这里就要用到我们前面计算的绝热过程温度递减率，如果环境温度递减率要大于绝热温度递减率，那么相对于环境，温度更高，气块会自发上升；相反，如果环境温度递减率，那么气块相对于环境更冷，气块下沉。
因此，我们有了下面的分类：

图3-5 大气静力稳定度分类
请注意：大气静力稳定度只是用来描述大气层结对气块的垂直运动产生什么影响（加速、减速或等速）的一个概念，这种影响只有当气块受到外界的冲击力以后才会表现出来，它并不表示大气中已经存在的对流运动。
条件不稳定是一种特殊情况，它对于饱和气块不稳定，而对干空气块是稳定的，它需要满足一定条件——空气必须首先抬升直至其变成饱和，进而变得不稳定。
对于条件不稳定的大气，如果遇到一些天气现象（如冷锋）强迫气流抬升，会使得原本稳定的大气变得不稳定，经抬升后变得不稳定的大气继续向上发展，会产生一些强对流天气现象（如雷暴）。
那么，原本的大气要抬升到什么高度才能变成不稳定呢？对此，我们定义了几个高度，来描述气块垂直上升时热力学状态发生改变时的高度，它们在气象学中都常用来进行天气学诊断。
抬升凝结高度（LCL）：示未饱和的湿气块被干绝热过程抬升至水汽饱和所需要的高度。
自由对流高度（LFC）：气块温度与环境温度之差由负值转为正值的转折点的高度。
平衡高度（EL）；上升气块遇到与自身温度相当的环境空气时的所在高度。
根据以上的高度以及计算的干湿绝热递减率，我们可以得到大气的状态与层结曲线。
大气的状态曲线，通常描述气块的绝热过程的曲线，而层结曲线，则表示大气的实际温度随垂直高度的分布。通过大气的状态曲线与层结曲线，可以判断当前大气的稳定状态。

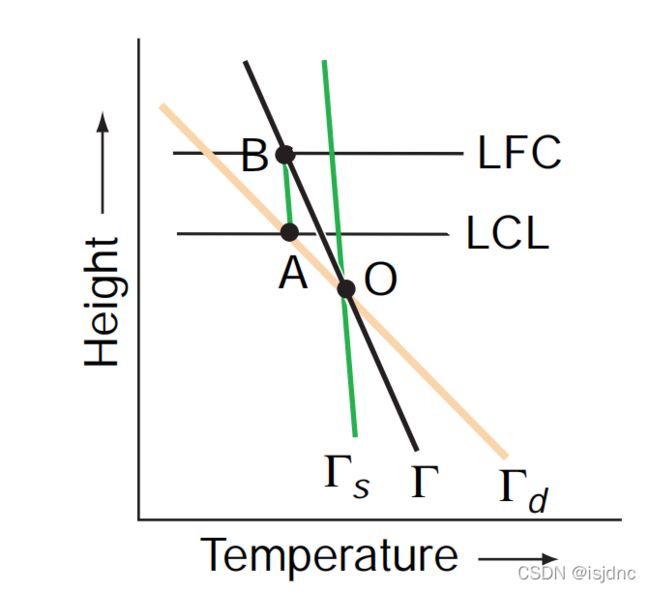
图3-6 条件不稳定状态曲线
如上图，对于条件不稳定大气，其温度递减率介于湿绝热递减率与干绝热递减率之间，假设一不饱和气块从O点出发，沿干绝热线上升，到达了抬升凝结高度A点。
注意，此时环境的温度递减率是小于干绝热递减率的，那么，对与气块来说，它的温度要冷于周围空气，如果没有外界的抬升作用，这个气块是无法继续抬升的，此时，气块稳定。
到了点A后，气块饱和，在外界作用下继续沿着湿绝热线上升，到了自由对流高度点B。由于湿绝热递减率要小于环境温度递减率，气块的温度逐渐向环境温度靠近，直到点B时，二者温度相等。若气块继续往上，其温度仍比环境温度高，则为自由对流高度，反之则为平衡高度。
在自由对流高度之上，气块温度高于环境温度，气块不需要外力抬升便可自行上升，发生对流，因此称为自由对流高度。
那么，在实际进行天气诊断时，我们如何得到这些参数，判断出大气的不稳定状态呢？为此，我们需要引入大气热力学图t-lnp图。
2.5 应用t-lnp图
相比起复杂的理论计算，热力学图更加直观简单，尽管误差较大，仍适用于精度要求较小的日常业务中。
在介绍t-lnp图前，我们先介绍几个大气热力学参数，这些参数描述了大气的热状态，通过这些参数，我们可以更好判断天气形势并加以应用于实际中。
位温Potential Temperature (Θ)：从原压强与温度出发，气体绝热膨胀或压缩到标准压强时(1000 hPa)的温度,在大气热力学中，位温是一个非常有用的参数，因为很多大气过程（短时间过程）是接近于绝热的，因此可用来比较不同气压下的气体热状态。
湿球温度Wet-bulb Temperature (Tw) ：对一块空气进行加湿，其饱和（相对湿度达到100%）时所达到的温度。 由于汽化潜热由空气块提供，故此温度低于乾球温度，也是当前环境仅通过蒸发水所能达到的最低温度。 湿球温度由实际空气温度（乾球温度）和湿度决定。
假相当位温Saturated Equivalent Potential Temperature (Θes) ：气块沿干绝热线上升到凝结高度后，再沿湿绝热上升，直到所含的水汽全部凝结脱落后，再沿干绝热线下降到1000hPa时所具有的温度。
湿球位温wet-bulb potential temperature (Θw)：湿球温度在潮湿绝热过程中，空气从初始状态冷却到饱和并达到1000hpa时所达到的温度。
相信看到这里，大部分人已经晕了。
上面所介绍的全部都是“描述大气热力学状态”的温度，它们表现了气块在大气中的热力过程，仅仅通过描述很难去理解，为此，我们需要借助T-lnp图来直观理解且获取相应的参数，并从中得到大气的不稳定状态。

上图为t-lnp图，红线为等温线，黑线为干绝热线，蓝线为等饱和比线，绿线为湿绝热线。
如何根据气块所在高度和气温，得到位温、湿球温度、假相当位温等参量呢？在t-lnp图中，有个最重要的规律—— Normand’s Rule，其描述如下图：

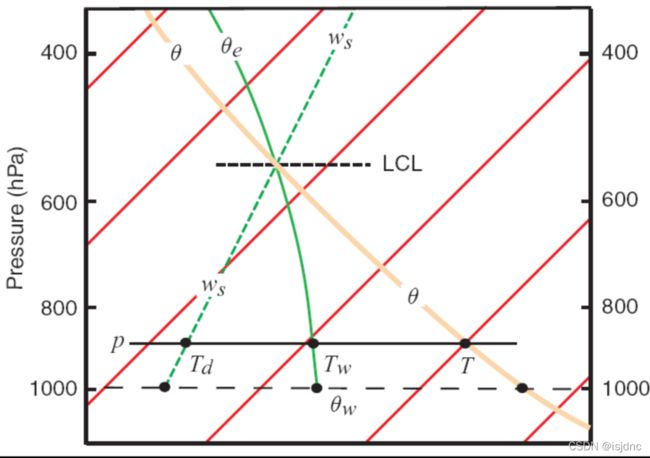
根据Normand’s Rule，只要知道气块温度、露点温度、湿球温度中的任意两个，便可得到气块的位温、湿球位温和假相当位温。
通过热力学图，我们还可确定对流有效位能（convective available potential energy, CAPE ）
对流抑制能（convective inhibition, CIN）
下沉对流有效位能（downdraft convective available potential energy, DCAPE ）雷暴最大上升速度（Maximum updraft speed in a thunderstorm）
冰雹大小（Hail size）对流上冲高度（Height of overshooting tops）等对流参数，关于这些对流参数的定义以及热力学图的具体应用，这里不多加介绍，
请有兴趣者自行参考T-lnp’s documentation

3、核化&云降水物理

在讲述本章前，思考一个问题：在上一章中我们提到，大气中水往往以气态形式存在，而我们所观测到的云、大气降水过程，水都是以液态、固态或者固液混合形态存在的。显而易见，其间必然涉及到了水的相变过程。
相变的过程必然涉及到了能量的转化与传递，那么，什么影响了相变过程？相变需要多少能量？相变后形成的水以什么方式存在？它的大小、数量、形状特征是什么？
转化成实际问题中，我们可以问：为什么云有不同的形态？为什么不同的云预示着不同的天气？为什么有时下雪、有时下雨？为什么雪有不同的形状？
从大尺度上，一般与大气环流、水汽条件、垂直上运动与来解释降水的过程。然而，这无法从根本上回答云与降水的形成，也无法具体解释人为活动对小尺度天气的影响。我们首先记住：云由一个个小云滴组成（可将其简单想象为极小的水滴），而一个云滴的形成与多个云滴共同作用涉及的微物理过程，云滴如何形成？如何增长？形成与增长过程中有什么规律？受什么条件影响？将是我们下文所需要讨论的内容。
本章主要内容如下图：

3.1 Köhler理论
我们知道，云由大量的云滴构成，云滴是指指半径小于100μm的水滴，而云滴生成增长会依赖于大气中水汽相变——即水汽冷凝形成液体云滴，从上一章可知，水汽想发生凝结，其气压e必须超过当前大气的饱和水汽压es。定义实际水汽压饱和比 ：
S = e/es
Köhler理论就给出了不同大小液滴与水汽的平衡时对应的理论饱和比Sk=er/es，当实际饱和比与理论饱和比不同时，液滴必然会增长或蒸发。
一般来讲饱和比与大气温度湿度相关，对云滴而言，其气压主要受两种因素影响，即：由于曲面引起的饱和蒸气压变化的Kelvin方程，以及结合了描述溶液蒸气压与其浓度关系的Raoult定律（溶质效应）。下面我们简单介绍这两种效应：
曲率效应（Kelvin方程）
在球形的云滴在其弯曲的液-气界面存在着一个非对称力：表面张力，其促使液体表面收缩，在液体表面相邻两部分之间互相牵引。
由下图，表面张力的存在会引起水滴内部气压的改变，由受力平衡，表面张力增加了水滴内部气压Δpdrop，其大小可根据水滴受力平衡来计算。
当水滴处于平衡时，内部压力（向外）抵消表面张力（向内）（此处忽略重力）
把一个水滴看做两个相同的半球，内部气压作用于水滴整个横切面Ac，而表面张力σLV作用于水滴的周长Lc，这两个力必须平衡，则有

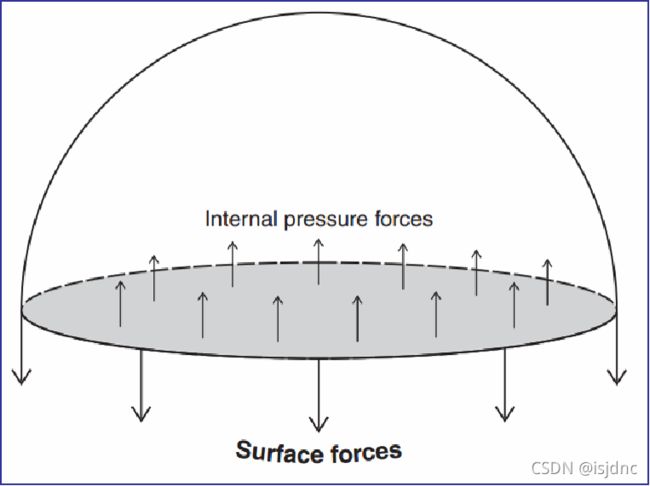
因此对于球形水滴，有：

称为Laplace方程，可以看出水滴内压随水滴增大而减小。
我们知道了由于表面张力会引起水滴内压的变化，那么，水滴内压的变化又是如何引起饱和比的变化呢？
彼此处于平衡的任意两个相态，它们的化学势相等。故，一个相态化学势的任意变化必然等于另一相态化学势的变化。
则有：

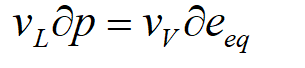
可得Poynting方程:

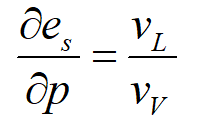
Poynting公式描述了总压力对平衡水汽压的影响。由于液相水分子所占体积 VL远小于相同数量气相水分子所占体积 Vv，因此平衡水汽压对总压力的依赖性相对较弱，仅为十万分子之一。但是该效应对云滴形成有重要影响。
在前文中，得到了表面张力引起的压力改变Δpdrop，在液相一侧，由于液态水不可压，可使用差分代替积分。则：

VL取为由1摩尔体积对应的液态水体积，则有：


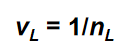
此公式描述了由于表面张力作用引起的化学势变化，它决定了水汽压e超过了饱和水汽压es多少。
在气相这一侧，可以根据理想气体状态方程Vv=RT/e，并对δμ积分，则有：

es为液面饱和水汽压，er为半径为r的水滴的平衡水汽压。
由Poynting公式：

变换便可得到得Kelvin-Thomson公式：

描述了表面张力σLV如何定量影响半径为rd水滴的平衡水汽压，这种由于液滴表面张力（曲率）引起的液滴平衡水汽压的效应，称为曲率效应，下图描述了曲率效应对于饱和比的影响：

值得指出的是，当曲率内凹时（r < 0），饱和比Sr会<1，称之为逆Kelvin效应。
溶质效应（Raoult定律）
在自然界中，水并不纯净，而是溶解了许多溶质，在大气中，水滴往往也会溶入许多杂质（可溶气体、气溶胶等）。
初中物理就告诉我们，在雪上撒盐有利于雪融化，这就是溶质的影响。溶质对于液态水平衡特性的影响称为溶质效应，其效应主要依赖于溶质量，也轻微依赖于溶质本身性质，其水中溶质可以降低水的平衡水汽压，使得熔点降低。
考虑溶液由水（溶剂，w）和普通非挥发性溶质（s）组成，其中溶质摩尔分数为χs。如果es表示纯水的平衡水汽压，Δe表示溶质效应引起的水汽压减少量，根据Raoult定律有：

即水汽压减少量与液体中溶质量成正比。
Δe为水汽压抑制量，Δe=es-esol,则esol为液面平衡水汽压，则平衡饱和比为：

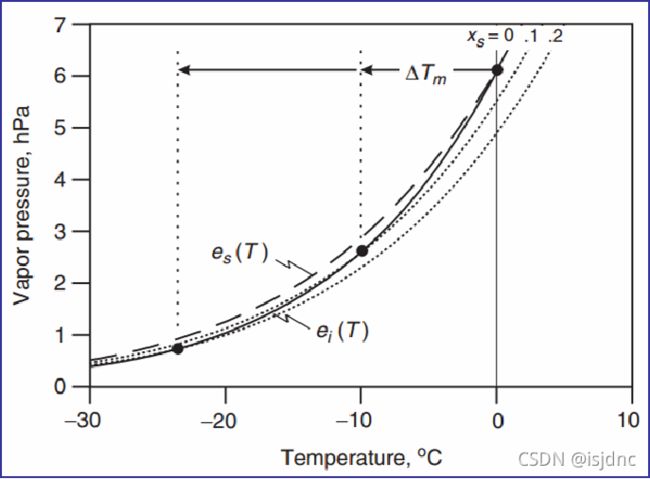
由于溶质效应对于平衡水汽压的影响，也可以降低冰点熔点。在大气热力学中我们讨论了液面饱和气压与冰面饱和水汽压温度曲线的差异。如下图，给出了不同溶质摩尔分数条件下，平衡水汽压随温度的变化。虚线为纯水标准曲线es(T)，实线为纯冰面曲线ei(T); 点线为两种溶液曲线（摩尔分数为0.1,0.2)。
可以看出溶液曲线与冰面曲线交点处存在新的固液平衡，即溶质的存在使得溶液的熔点相对于纯水有一个一个偏移，称为ΔTm，溶质的存在使得溶液有了一个新的固体-溶液平衡点。显然，溶质越高，溶液水汽压被抑制，迫使熔点降低越多。

由于自然界中，大多数大多数溶液并非是理想的，溶液中溶质分子通常与水分子有复杂的相互作用。为了避免这些复杂性，在Raoult定律中，不采用实际的摩尔分数χ（溶质或水），而采用活度α，可写成：

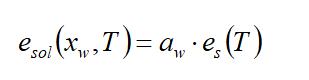
αw为水的活度，是实际水摩尔分数 χw的函数，也与其他特性有关，通常，活度有3种表现形式：
1、定义为摩尔分数与活度系数的乘积，活度系数γj考虑了所有非线性效应。

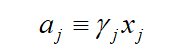
2、采用van’t Hoff因子(i)进行修正：如果单位体积溶液包含ns摩尔溶质、nw摩尔水，则水活度为

3、通过溶质的渗透压效应（osmotic pressure）进行计算。
Köhler理论
云滴的形成需要三个主要条件：湿度、气溶胶、冷却（Moisture, Aerosol, Cooling: MAC），气溶胶作为溶质降低水汽的平衡水汽压，促进大气中的水汽凝结。
前面介绍的两个效应刻画了大气液滴的基本属性：曲率、溶质含量，曲率增加平衡水汽压，而溶质降低平衡水汽压，两个属性在对粒子中水的影响相互竞争。
对于纯水滴（半径为rd），曲率与水汽压关系为Kelvin-Thomson方程：

溶质效应为Raoult公式，最常用形式为：

将两个公式相乘，可得Köhler理论方程：

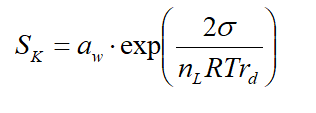
Sk即为Köhler理论饱和比，可绘制Köhler曲线。

Henry定律
实际上，大气中存在许多挥发性溶质，我们需要考虑它们在大气液滴中的可溶性，我们需要计算它们在云滴溶解量，再估计它们对平衡水汽压的影响。
考虑有痕量气体A溶解于云水，处于平衡状态时，有：

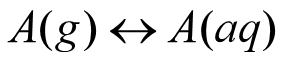
即：A气相分子进入水相速率 = 逃离水相进入气相的分子速率。此时，水相中A的分子浓度是稳定不变的，与气相中A的分压（ pA,sol ）成正比。根据Henry定律：

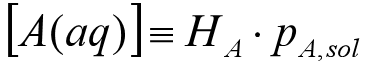
比例常数HA（常用单位：mol L^-1 atm ^-1）称作A的Henry定律系数，用来表示气体A在水溶液中的可溶性，即每单位分压（一般1atm）单位体积（一般为1L）溶液中A的溶解摩尔数。
需要指出的是，传统Henry系数直考虑了物理溶解过程，气相和水相都以分子形式存在，却没有考虑溶质在水中的电离、反应过程，为了考虑为了考虑离解效应，需要引进总体Henry定律系数（HA*）。
总体Henry律系数考虑了痕量气体的物理吸收和离解，表示一定pH值液体中气体的完整可溶性。

上图给出了部分气体总体Henry律系数随溶液pH值的变化，不同物种气体的可溶性变化范围很宽。不难看出，酸性气体（HNO3、SO2）随溶液pH值增加而更加可溶，但碱性气体（主要是NH3）则相反，尽管H2SO4为酸性气体，其在水中的可溶性极强，pH对其的影响反而可以忽略。而溶解气体（但不离解）的Henry律系数。这些非反应性成分的Henry律系数与溶液pH值无关，因为这些成分是电中性的，不改变溶液中的离子平衡。
根据Henry定律，我们可以推导出水活度与摩尔分数间的关系：

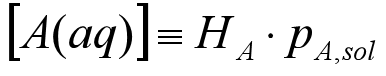
根据水活度的定义，可写为：

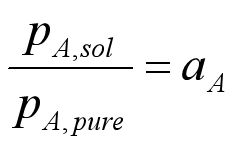
则：

当溶液浓度较低（nA<
可以算出溶质活度：

这时请注意：Henry定律影响的是溶质活度，而前文提到的Raoult律的影响为水活度，那么，它们之间有何关系呢？

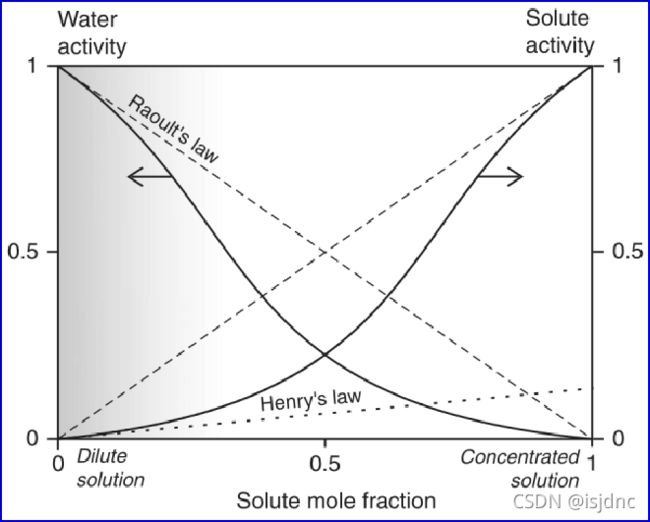
上图给出了水活度αw与溶质活度αA随摩尔分数的变化，不难看出，由于Henry定律影响，相对于Raoult律（虚线）而言，水与溶质的活度（αw、αA）都受到抑制，
在摩尔分数较低时，溶质活度αA的规律更符合Henry定律的变化，而随着摩尔分数的增加，其变化开始向Raoult律靠近，因此，对痕量气体我们采用Henry律、对于一般溶质采用Raoult律。对于云水而言，一般摩尔分数较小，其特征更符合左端变化。
当液滴开始吸收可挥发的痕量气体时，Köhler理论依然适用，不过其溶质量不在固定，需要考虑随着液滴半径变化的溶质量，
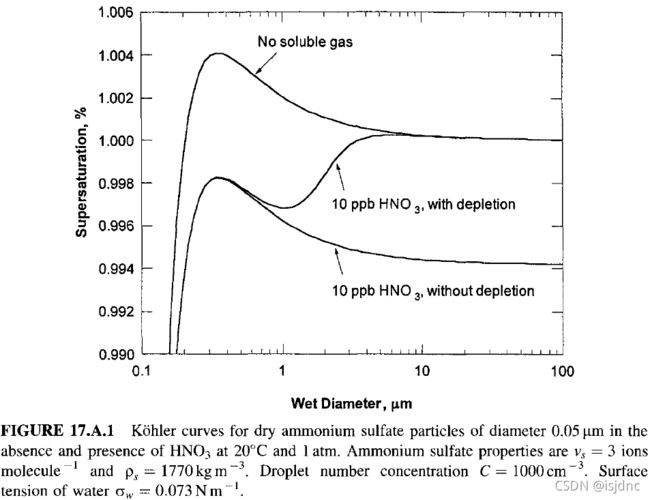
此问题非常复杂，这里，我们用图来简单描述一下挥发性气体对理想Köhler曲线的影响。

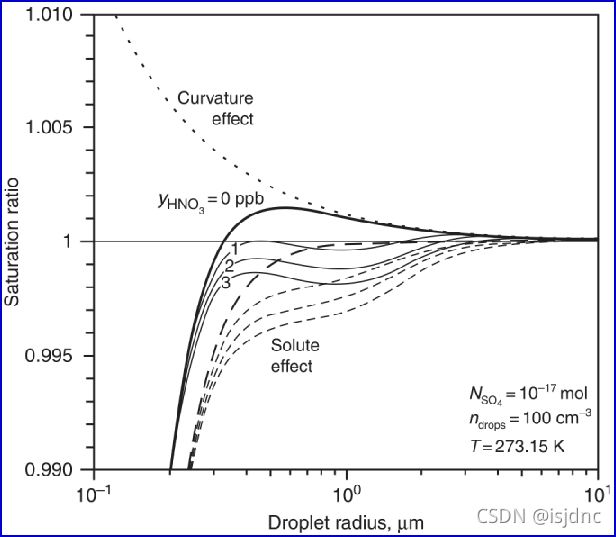
假定溶质含量固定，四条实线分别代表硝酸初始混合比为yHNO3 = 0, 1, 2, 3 ppb时的计算结果；每条实线在下方都有对应的虚线，表示溶质效应（硫酸+硝酸之和）。
最上方的虚线为液滴曲率效应（假定表面张力不变）, 最上方实线即为非挥发性溶质的常规Köhler理论。
在左侧，液滴较小时，硝酸对液滴的影响很小，主要由硫酸控制，曲线与常规Köhler曲线一致。随着液滴逐渐增大，水分，稀释硫酸，开始吸收硝酸，溶质含量增加进一步抑制水蒸发。与仅有非挥发性溶质项比，第一极大值饱和比明显减小，硝酸开始控制曲线。
当所有液滴都吸收硝酸时，硝酸气体供应逐渐减弱，后续吸收效率降低；则由于液态水的增加导致硝酸变得稀释，所以平衡饱和比又上升并超过极低值，随后，液滴继续增长，接近纯水滴，不再考虑硝酸影响。
若硝酸的提供不限，则曲线的饱和比下降，但变化特征与理想曲线一致，

3.2 核化理论
上一节，我们介绍了Köhler理论，描述了不同大小的液滴的吸湿特性。但是我们应当注意到一个问题：大气中的液滴如何而来？最初的云滴是如何在大气中形成的呢？这里，我们就需要介绍核化理论。
核化（nucleation）是凝聚态（液态、固态）触发的过程，由热力学常识可知，新相态的形成必须满足一定的热力学条件：新相态（子相）摩尔自由能（即化学势）必须小于原相态（母相），才能维持下去。
核化可以分为两类：
均相核化：均一母相，没有外部介质（O2、N2不参与）
异相核化：多相态，有外部介质参与。
潮解与风化
当纯气态物质自发生成纯液滴时，该过程称为均相核化（空气存在并不影响该过程），该过程需要极高的过饱和度才能实现，在实际大气中，均相核化几乎不可能发生，需要依赖异相核化形成云滴。
任何促进新相态形成的物质(nucleating agent)称为成核剂，它降低新相态形成所需要的自由能大气中，气溶胶颗粒可以充当成核剂起作用，称为凝结核。

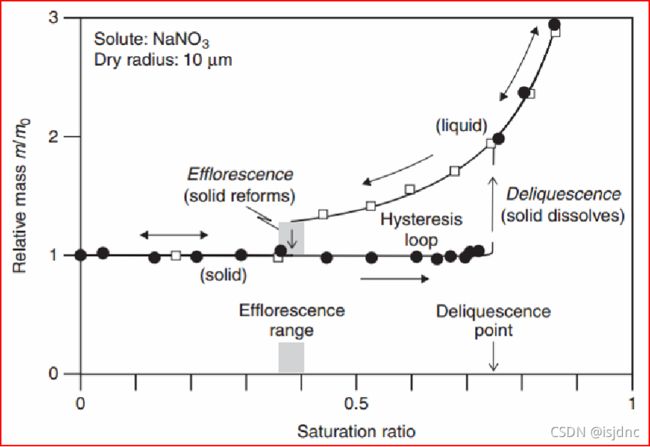
可溶性物质可以抵消小粒子的曲率效应，可以高效触发液相。上图中，我们可以看出可溶颗粒在不同饱和比条件下的相态变化过程，很明显在潮解点发生了非线性的溶解过程。
在初始干粒子表面，当水分子累积速度大于逃离速度时，液态就开始了。相对湿度低于100%时，固体溶解形成溶液的过程称作潮解。
当湿度低于潮解点时，干粒表面吸附水汽分子，但水量不足以破坏晶格；随着湿度增大，吸收水份增加，最终溶解无机盐。
由于水汽压降低（溶质效应）导致从环境中吸收更多水分子，进一步溶解固体；水汽吸收过程持续，直至固体完全消失，整个粒子变成液体溶滴的一部分。
在固体变成液体的过程中，熵是增加的，因此潮解是平衡变换，不是核化过程（熵减小过程）。
当饱和比降至溶解点之下时，随着环境湿度不断下降，液滴蒸发失去水分，溶质浓度升高，则溶液变得相对于固体溶质为过饱和，降至某一点，溶质过饱和度达到阈值，此时固体溶质成核，则原干粒子无机盐重生，该过程称为风化，为核化现象。
活化
形成云滴要求液体溶滴（即霾滴、液态气溶胶）必须活化。活化类似于水滴核化，也需要克服自由能障碍。因液相已（通过潮解）存在，故活化不是相态核化现象，而只是随着环境湿度加大从稳定增长变为不稳定增长。
根据Köhler理论，可知在某一半径r时，Sk达到极大值，该半径称为临界半径rc。
半径小于rc的液滴为霾粒子，而大于rc的液滴为云滴。
活化即为霾滴增长超过Köhler函数峰值并转变云滴的过程。
霾粒子与云滴的区别在于增长/蒸发特征对于扰动的响应。
霾滴半径小于rc，位于上升支，梯度dSK/drd > 0，稳定平衡态
云滴半径大于rc，梯度dSK/drd < 0，不稳定平衡态。
稳定平衡与不稳定平态的似乎听起来有些抽象，这里，我给出自己个人的理解与描述：
如下图，我们分别给霾滴与云滴一个扰动，让它们脱离原本的平衡态。
即：假设一个小液滴，分别与一个霾滴和一个云滴合并。显然，霾滴与云滴的大小会有所增长。
然而，此时霾滴的半径并未超过临界半径rc，霾滴半径增长。它所对应的平衡饱和比也会增长，此时，环境饱和比无法与增长后的霾滴维持平衡，此时，霾滴便会蒸发，直到其平衡饱和比与周围环境饱和比再次相等。结果是：霾滴又恢复到了原来的大小。
对于云滴，由于其半径早已超过临界半径rc，其对应的平衡饱和比随着其半径增加反而下降，此时，云滴将无法返回原来大小，而是继续从外界环境吸收水汽不断增长。（因为外界环境饱和比>平衡饱和比，且平衡饱和比随云滴增长不断下降）
简而言之，就是：未活化的霾粒子在扰动下可以恢复原来的大小，而活化后的云滴将会不断增长。

3.3 暖云过程
在上面我们讲了大气中的云滴是如何产生，受哪些因素影响，而这一讲中，我们需要讨论生成的云滴如何增长的过程。
我们提到了，活化后的云滴会不断从外界吸收水汽增长，那么在一定的条件下（温度、气压、过饱和度），云滴将会如何增长？其机制如何？
在暖云（云体温度在0℃以上，只由水滴组成）中，云滴的增长主要涉及两种机制：
1、凝结增长，云滴捕获外界水汽，使得水汽在云滴上凝结，这种增长机制按分子增加，速率较慢，适合生成比较小的云滴。
2、碰并增长：云滴捕获其他粒子增长，即，较大的云滴可以捕获较小的云滴，二者合并形成更大的云滴，这种方式增长较快，但需要云滴达到一定大小。
当然，实际过程二种机制可以同时发生，但为了方面，我们会分别介绍。
当云滴增长到一定程度时，云滴下落，变为雨滴。这就是比较经典的暖云过程，下面，我们将逐一展开介绍这些过程。
凝结增长，
从定义不难看出，凝结增长需要涉及到相变过程，水汽需要凝结液化，根据前面的介绍的核化理论，我们不难知道，水汽凝结的驱动力为过饱和度之差，环境的过饱和度需要＞云滴自身的过饱和度，云滴会凝结增长否则，云滴不变或蒸发。

考虑单个云滴的凝结增长，这里介绍最经典的Maxwell增长理论。其假定条件为：

Maxwell增长需要三个步骤：
1、质量输送，水汽分子扩散至液滴表面。
2、表面过程：水汽相变，释放出潜热。
3、能量传输：凝结释放出的热量输送至外界。
假定水滴表面水汽分子通量是均匀的且垂直于表面，则水滴质量md增长速率为：

其中Mw为水的摩尔质量，Φv,sfc为水滴表面水汽通量Φv,sfc = -Dv(dn/dr)rd，则

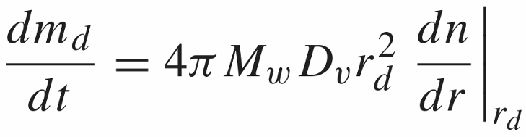
或者，我们也可以将其写作：

为了简化方程，我们假设了水滴周围存在平稳扩散状态，对于平稳扩散而言，水汽质量输送与x无关，那么，我们积分得到：

将M=4/3Πr³ρl代入，我们得到：

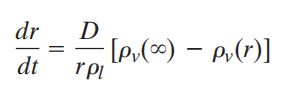
使用理想气体状态方程：

在根据我们过饱和度的定义，最终，我们得到单滴凝结增长方程：


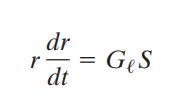
对于一个确定的环境，G可以看作一个常数，根据上述公式，我们不难发现液滴凝结增长的规律：液滴凝结增长速率与液滴半径呈反比。
然而，在实际情况中，有许多个小液滴同时凝结增长，它们会一起争夺环境中的水分，使得环境饱和比下降更快。
群滴凝结增长方程需要考虑饱和比变化，这里，我不给出推导过程，只给出最终结果：

饱和度的变化主要由生成项（干绝热上升）-损失项（潜热释放）。
在实际大气中，不饱和的气块包裹着大量液滴向上干绝热增长，膨胀冷却，最终达到饱和。
随后，气块进一步抬升，气块中的CCN率先被活化为云滴，当由绝热冷却得到的水蒸气超过饱和的速率等于水蒸气凝结到CCN和水滴上的速率时，云中的过饱和达到最大值，云内的云滴数量达到稳定。
此后，云滴增长消耗的水汽快于空气冷却造成的过饱和水汽，因此过饱和度开始下降。
因为凝结液滴的生长速率与它的半径成反比，较小的云滴比较大的云滴生长得更快。因此，在这个简化模型中，云中的液滴的大小随着时间的推移变得越来越均匀(即液滴趋于单粒径分布)。所有过程见下图：

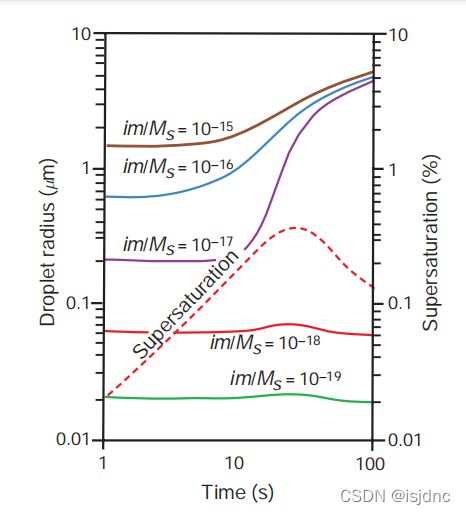
碰并增长
在暖云中，云滴凝结增长可以获得较小半径的云滴，但是，如下图想要获得较大的雨滴，仅依靠凝结增长无法实现，这时，雨滴的形成需要依赖碰并增长过程。

下图给出液滴生长的时间曲线，蓝线表示凝结增长，红线为碰撞增长，不难看出，当液滴半径到达一定大小时，碰并增长开始变得重要。

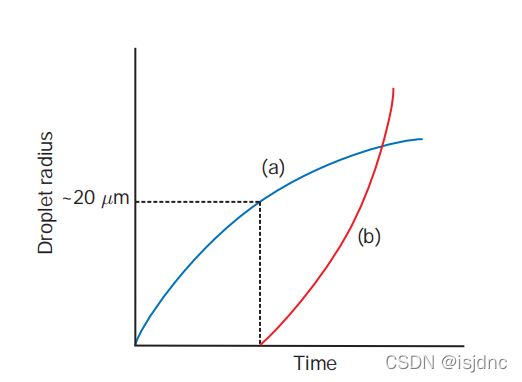
我们知道，想要两个粒子间发生碰撞，需要两个粒子间产生相对运动，能够使得捕获滴与被捕获滴在空中某一时刻能够相遇发生碰撞。
由初中物理中，物体从高空下落通常做自由落体运动，拥有相同的加速度，使得它们无法完成相遇。
然而，对于小液滴而言空气的摩擦阻力不能忽略，对于液滴，除了重力外，还受浮力与空气拖曳力影响，使得不同大小的液滴具有不同的末速度（最大下落速度），使得液滴间的碰撞成为可能。
下面对液滴的下落末速度进行讨论：

静止时，液滴仅受重力作用，一旦液滴开始运动，挤开空气，产生空气拖曳力：FD= FD(vp’) （vp’ 相对于空气的速度）。
粒子从初始静止（ FD= 0）状态加速， vp’随时间增加，直至FD(vp’) =FG
一旦达到受力平衡，不再加速，则此最大下落速度称为下落末速度vp。从静止到最大速度的时间称为弛豫时间，依赖于粒子质量、大小；在气象中我们通常忽略弛豫时间，将云粒子视为一下落便到达末速度。

拖曳力FD正比于动压和粒子横截面大小，可以写作：

CD为拖曳系数，是所有非几何因素经验因子，本身也依赖于vp，
根据末速度定义，我们有：


尽管我们并不清楚CD的函数表达式，但仍然可以看出末速度的以下特点：
1、末速度依赖于粒子重量（ρpVpg）与有效横截面（ ρairAC，即粒子运动挤开的空气量）之比，故紧致大粒子末速度大，小粒子末速度小；
2、末速度随空气密度增大而减小。
为了进一步探寻不同大小粒子末速度，我们引入雷诺数来简化该式。
雷诺数为描述流体状态的一个重要无量纲数，为惯性力与粘性力之比：

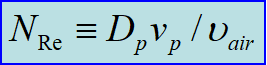
于是我们将下落末速度表示为：

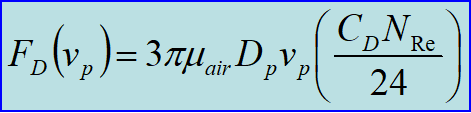
末速度的大小与粒子大小相关，将粒子大小空气分子平均自由程λair ~ 0.1 μm）比较，可以将其分为几个体系，不同的体系，末速度与粒子大小具有不同的关系。

对于自由分子体系λair>>Dp：
末速度与微粒直径成正比。
对于过度体系λair~Dp：物理机制复杂，通常采用Cunningham滑流订正因子订正。

对于连续介质体系：λair< Nre<<1：此时，粘性力很大，连续介质体系I也称作Stokes体系，其特征是粒子周围的缓慢蠕动流或爬流。末速度正比于粒子直径的二次方：

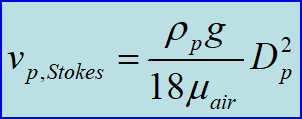
连续介质体系II与连续介质体系III均无拖曳力解析解，此处不再赘述。
下图给出了不同体系中的末速度，总体而言，虽然末速度的体系转化存在不确定性，也很难计算出准确末速度，但总体来说，末速度还是随粒子大小单调递增。

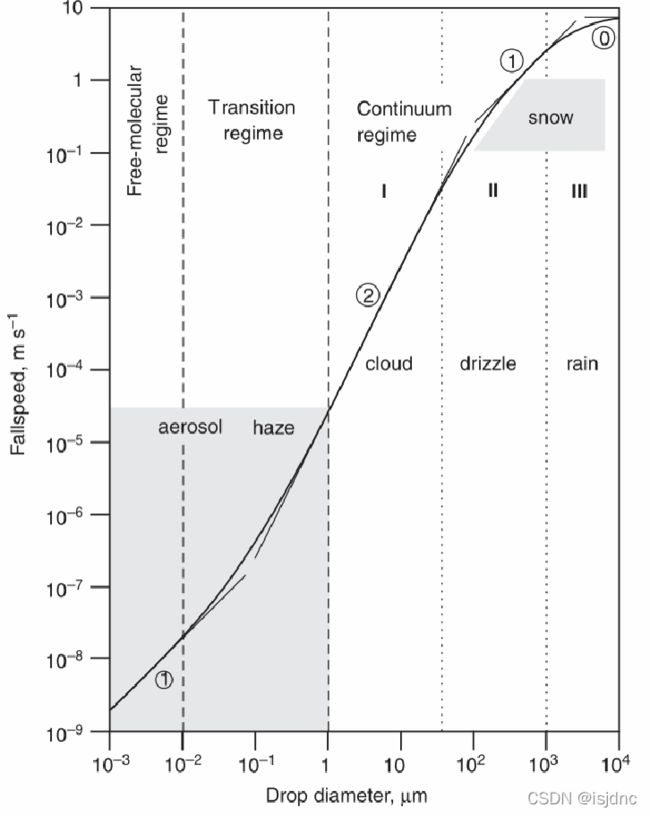
碰撞效率
如下图，我们考虑一个半径为r1的液滴(称为捕获滴)，它正在超越半径为r2的小滴(图6.19)。由于空气的扰流作用，液滴会绕开捕获滴使得二者间无法发生碰撞，此时，就存在碰撞效率的问题。

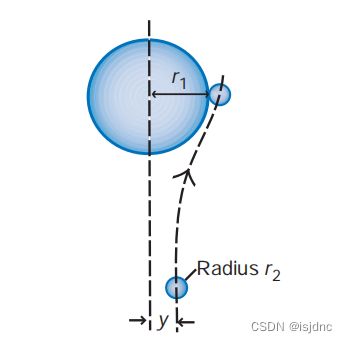
为了表示成功碰撞的几率，引进碰撞效率 E，定义为成功碰撞事件（实际碰撞）与所有可能碰撞（即捕获滴扫过几何体积内的小滴）数量之比。

Aeff为有效碰撞面积，有效碰撞截面半径为 yc。

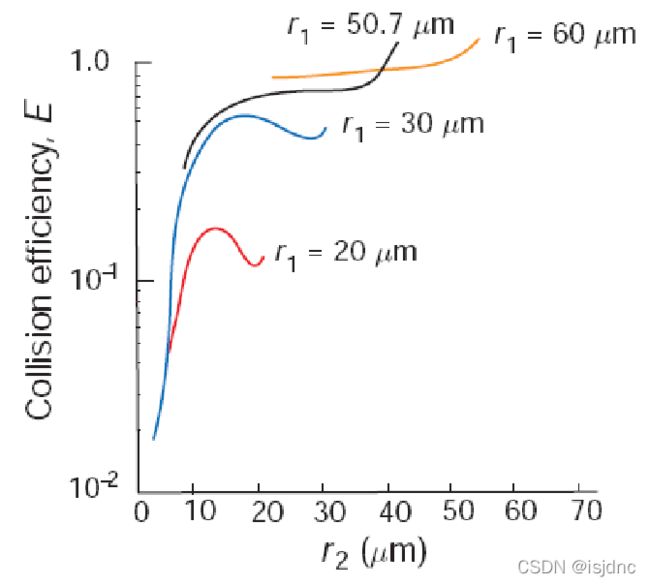
上图给出碰撞效率与捕获滴半径和被捕获液滴半径的关系，当小滴半径低于5μm时，不管捕获滴有多大，E都很小，小水滴因惯性小，跟随空气运动，被空气拽着绕过捕获滴。
一旦小滴半径超过5μm，碰撞效率增加很快。因为水滴质量随半径三次方增加，即惯性增加很快，对空气的突然侧向加速不能及时响应，因此与捕获滴相碰撞几率增大。
对于很小的捕获滴，E的最大值也很低，真正有效的捕获滴其半径需要超过20 μm 。
E达到最大值后减小，这是因为捕获滴与被捕滴的下落末速度相似。
但是当捕获滴与被捕滴大小几乎相同时，E值又增大，这是因为尾流效应（wake effect）：位置较低水滴使其尾流处流场变形，使尾随水滴以比自由流中末速度较快的速度下落，从而赶上较低的水滴。
当捕获滴的半径超过当捕获滴的半径超过~ 50μm且被捕滴半径大于 ~10 μm时，碰撞效率接近于1。
合并效率
发生碰撞后，会发生以下情况：

• 合并（coalesce，合并成一个水滴）
• 回弹（rebound，彼此弹开）
• 破碎（disrupt，分裂成若干个小水滴）

若想要通过碰撞使得液滴增长，液滴发生碰撞后，必须合并，这是直接导致捕获滴增长的唯一方式。引起合并的碰撞称为碰并，是形成捕获增长的基础。没有碰撞就不可能有合并，所以捕获效率Ec是碰撞效率E与合并效率ε之乘积。

合并效率的确定与解释都是基于实验室实验的结果。实验发现：小的被捕滴容易合并，而较大的被捕滴容易弹开。
基于此，提出了假说：液滴弹开是由于水滴变形，以及碰撞时两者之间夹了一层空气，为此，定义Weber数，来描述流体的形变。
Weber数为动压力（作用于液滴使其变形的外力）与表面张力（阻止变形的粘合力）之比。

合并效率就是Weber数的函数，随Weber数增大而减小。
将二者结合，便得到捕获效率：

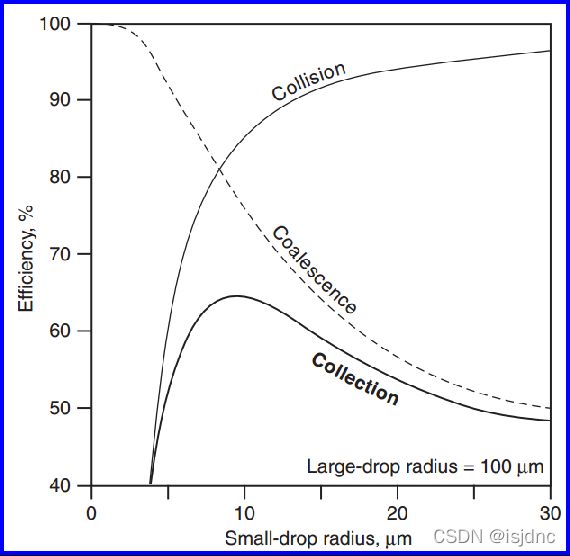
上图给出了捕获滴半径为r~100μm时的三个效率曲线，当被捕滴半径超过5μm时，碰撞效率增长很快。
合并效率则在被捕滴很小时很大，并随着半径的增大而快速下降。
两者之乘积给出碰并效率的净效果：开始时Ec很小，在中等大小时出现极大值，但又因为合并效率而逐渐下降。
捕获模型
连续捕获机制假定在一群小云滴中至少已经存在几个大水滴。
如图所示，不需要考虑单个碰并事件，而是把小云滴群当作连续体，捕获滴以连续而均一的方式与均匀分布的小滴碰撞。

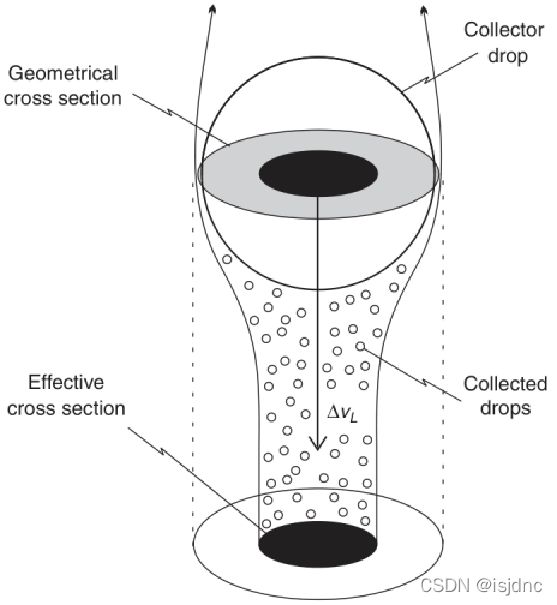
在这种模型下。同样大小的捕获滴穿过同样的云时将以相同的速度增长，云滴尺度分布比较均匀。
连续捕获模式揭示了云滴增长规律，但没有解释自然中少部分云滴便可快速形成云的现象，仅靠连续增长，云的增长效率并不高，这是，又有另一个模型——随机捕获模式。
随即捕获模式
随机捕获模式认为碰撞是一个一个的单独随机事件，这些事件在空间与时间上是统计分布的。
假设有100个液滴，初始时刻大小同样(L1)。
一段时间后，部分液滴(比如10个)与小滴碰撞，则分布发生变化(L2); 由于半径较大，这10个大滴就处于进一步碰撞的有利条件。
第二次碰撞同样是统计分布的，进一步加宽液滴尺度谱（L3） 。

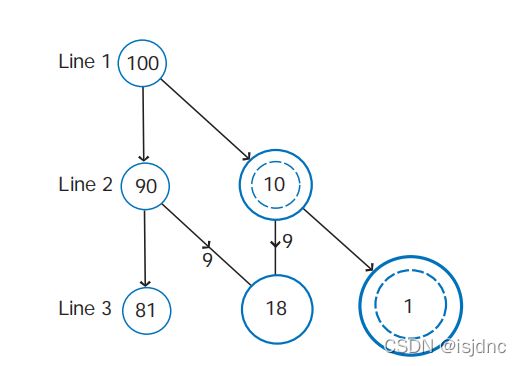
在这样的模式下，云滴迅速加宽。原本均匀的云滴谱开始加宽。少部分云滴通过统计分布碰撞而比一般云滴增长快得多，这也可以解释典型海洋的暖积云的形成，
小结
现在，我们已经知道了基本的暖云过程：
空气中的颗粒（气溶胶）通过异相核化，生成了小液滴，这些液滴有的被活化变成云粒子，未被活化的称为霾粒子，而云团就是可增长云滴 + 不可增长霾粒子的混合的胶体，霾粒子分布在云滴间隙之间。
我们看到的云，就是大量的云滴对太阳光的散射。
初期形成的暖云是个稳定的胶体系统，只是大量小水滴的混合物，可以存在较长时间。
但是，由于碰并增长，水滴的不断增大，大水滴消耗了小水滴，平衡态打破，最终形成降雨（云消散）。
不过，碰撞的启动通常需要水滴之间存在较大的相对速度，需要较大捕获滴的存在，凝结增长通常很难形成满足要求的大小云滴，那么在碰撞发生之前的较大捕获滴是从何而来呢？这是目前暖云过程的空白部分。
3.4冷云过程*
在天气学中，“降水”与“降雨”的概念并不相同，降雨可以称为液态降水过程，但是降水过程是包括固态的，通常见到的降雪、冰雹等，定义为固态降水现象。
那么，大气中的固态降水是从何而来呢？很显然，仅有液态水滴构成的暖云无法满足固态降水的需求，于是，另一种过程，冷云过程需要开始被关注。
什么是冷云？我们知道云有一定高度，而到达一定高度时，周围环境气温会小于0℃，达到水的凝固点。当云伸展到0℃高度以上，则称之为冷云。
云中温度低于0℃的部分，仍可能存在液态水滴，则这些水滴称作过冷水滴。
如果冷云中既包含冰粒子又包含过冷水滴，则称为混合云；如果它全部由冰粒子组成，则称之为冰云。
冷云的微物理过程与暖云过程比较相似，不同之处在于，冷云涉及到的一个新的相态——冰相。而冷云微物理学，主要讲述冰相的形成、增长过程。
冰相均质核化
大气中冰相的形成主要有两个路径：1、水汽直接凝华（直接路径），2、先凝结形成液相再冻结（间接路径）。
在均相核化过程中，除非有着极罕见的低温（-100℃，否则直接路径很难发生，通常，水汽应通过间接路径变成冰。
水汽的凝结过程，在核化理论中已经介绍，下面介绍过冷水的冻结过程。
液态水自发冻结的条件。与气态到液滴均相核化一样，需计算母相（过冷水滴）中子相（冰）胚胎形成过程中系统自由能的变化。
如下图，在冻结过程中，过冷水滴形成晶格，集聚形成冰胚，核化速率与冰胚浓度相关。

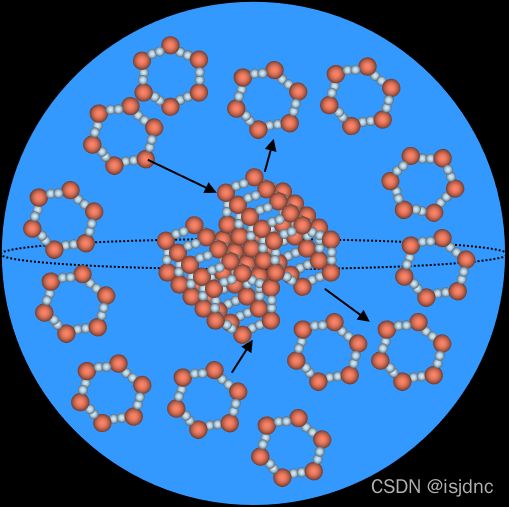
冰胚（germ）浓度可根据热力学Boltzman分布得到：

NL为液相分子数浓度。
核化速率为：

J1为临界冰胚从母相获得分子的速率，其形式比水汽核化生成液滴复杂。这里不介绍J1的推导，只给最终结果：


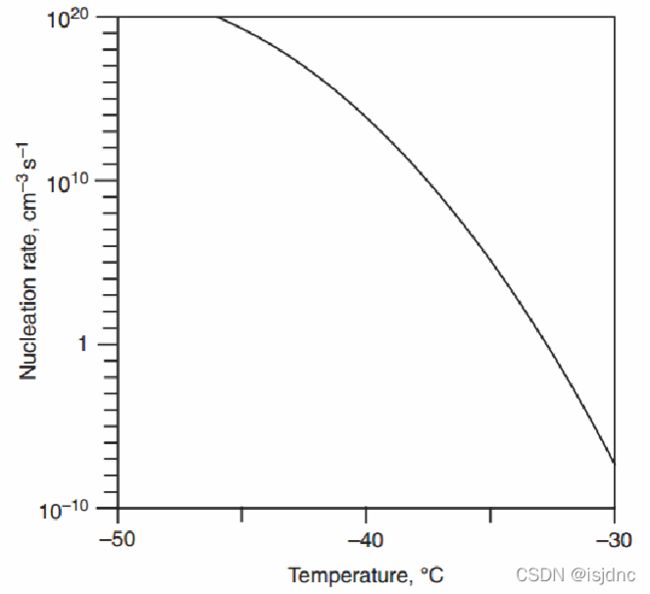
上图给出了冻结核化速率与温度关系图，可以看出，它们主要呈现出指数函数关系。
Ji(T)为单位容积冻结速率，它是温度的函数，但是它并不能用来判断冻结的发生。仅有一个核化事件就足以引发整个水滴发生冻结，而不管其大小。所以，重要的变量是核化频率ωi = VdJi(T)，即水滴体积与核化速率之积，而非Ji(T) 。
水滴体积越大，则意味着只需要较小Ji(T)就可得到相同的冻结效果；同理，体积越大，获得临界冰胚的机会越大。因此，阈值条件的选择（即选择某一显著核化速率）依赖于过冷水滴体积以及温度。通常选择核化频率 ωi = 1s^-1作为均相冻结的标准。
对于纯净云滴，其直径一般为20μm，其均相冻结温度为≈235K。
对于不纯净的水滴，其冻结受溶质效应影响，冻结温度与水活度相关。

上图体现了水活度影响冰熔点温度和水溶液的冻结。高浓度液滴必须克服溶质的熔点效应，即通过增加水分子，使之偏离固-液平衡而进入过冷（亚稳定）区域，溶质效应可以抑制水滴的冻结，冻结温度可以看作水活度的函数，冻结曲线只是熔化曲线向高活度（左）平移了Δaw 。
冰的异相核化
和水的均质核化类似，冰的均质核化通常需要极低的温度才能发生冻结，需要外来非水相颗粒促进核化过程，这些粒子是气溶胶的一部分，称作冰核（IN）。
下图给出了冰粒子直径与温度的关系，红线为异相核化，蓝线为均质核化。异相核化提高了冰粒子的生成效率，使得成冰温度大幅度上升，异相核化冻结温度随着水滴直径增加而升高；即在给定温度下，水滴体积越大越容易核化 。


IN为液态水提供形成冰结构的表面，使得冰胚粒径增大，使得冻结发生在高于均相冻结的温度条件下。
IN性质，在定性与定量上，都与凝结核CN不同。

• 最有效CN（例如CCN临界过饱和度只有百分之几）由可溶物组成；而IN一般不可溶，且具有与冰Ih六棱晶格相关的晶体结构。
• 大气中IN与CCN代表大气气溶胶中相互排他的子集，但是混合粒子（即既含有不可溶又含有可溶成分）很普遍。
• 大气中IN浓度远小于CCN浓度。
• 异相核化发生在IN表面，而均相核化在水滴内部随机引发。

IN可分为：侵润核、接触核、凝华核、冻结核，它们均可引起异相核化，但核化方式不同，目前主要有四种核化机制。

• 接触冻结（液面过饱和、过冷水滴）Contact 过冷水滴一接触冰核就迅速冻结。
  

• 凝结后立刻冻结（液面过饱和、水汽）Condensation followed by freezing
  先充当CCN，然后不可溶部分冻结水滴
  

• 浸入（浸润）冻结（液面过饱和、过冷水滴）Immersion 冰核进入过冷水滴后再冻结
  

• 凝华（冰面过饱和、水汽）Heterogeneous deposition 直接由水汽凝华生成冰晶
  
  冰核（IN）浓度没有系统变化，观测出的IN浓度十分离散，原因主要有：
  1、IN数与气溶胶类型有关，因此与气团离开气溶胶源的中间历史有关。例如IN-暴：一天内IN浓度陡增，比典型值大几个数量级；几天后，同样急速下降。成因：外星源（急流附近富含冰核平流层空气下沉）、火山喷发或沙尘暴、云核降水粒子的蒸发。
  2、IN浓度测量技术。有人认为广泛使用的经典过滤技术测量IN浓度比连续气流箱技术低估一个量级。在相同温度下，接触模态IN要比浸没或凝华模态大一个量级。
  3、IN浓度对相对湿度的依赖性。研究发现，在任一给定温度下，IN数浓度随着冰面过饱和度的增加而增加
  冰晶浓度
  在实际观测中，冰晶的数量要远大于冰核数目，冰晶粒子浓度比冰核浓度观测值高几个量级。原因为由一次冰晶生成的二次冰晶增大了冰晶浓度。
  一次冰晶：水汽凝华、过冷水滴凝结形成的冰晶。
  二次冰晶：由于一次冰晶破碎，或冰晶繁生形成的冰晶。
  高浓度的冰晶可能由于目前冰核观测技术在某种条件下，尚不能可靠地估计自然云中活化冰核浓度；也由于有些冰晶易碎，与其它冰晶粒子碰撞时，会破裂成许多碎片；也可能是由于所谓的冰晶繁生（或冰晶增生）过程。
  冰晶繁生过程如下：
  当一个过冷水滴与一个冰晶粒子碰撞冻结时（云滴在冰晶粒子上的冻结过程称作凇附），冻结过程分为两个阶段。
  第一阶段的出现几乎是瞬时的，一个细密的冰网迅速穿透云滴，使其中部分液水冻结，潜热释放恰好使该云滴温度增至0C。
  第二阶段很缓慢并把热量从部分冻结云滴传到较冷的环境空气中。首先在云滴表面形成一个冰壳，然后冰壳不断向内加厚；液水被困在内部；当液水冻结时，体积膨胀，对冰壳产生很大的压力。这些压力可导致冰壳破裂甚至爆炸，抛出许多碎冰屑。
  冰晶增长
  考虑单个冰晶粒子的凝华增长，与液滴凝结增长类似，但由于冰相与液相的差距，依然存在着区别。
  由于冰不易变形，且晶体形状复杂，溶质效应与曲率效应对其影响较小。
  由于冰晶形态复杂，套用静电学中电容(capacitance)概念对其描述。
  
  
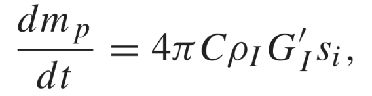
  其中GI为冰粒子增长参数，是温度T的函数。C为冰晶粒子电容，与粒径大小有关，量纲为距离，也受形状的影响。
  
  上图给出了液面饱和条件下，GiSi随温度而变化 ，在–14℃左右达到极大值，主要因为这时液面与冰面饱和水汽差异最大。因此在混合云中，冰晶通过水汽凝华增长在–14℃左右质量增长最快。
  冰晶凝华增长主要通过Bergeron过程，由于液面饱和和冰面饱和间的差异，当环境达到冰面过饱和和液面未饱和时冰晶粒子增长速率要远快于云滴凝结增长。如果冰晶粒子增长导致其附近水汽压低于液面饱和度，则附近的云滴将蒸发掉。
  
  除去凝华增长外，冰晶增长还存在淞附过程和丛集增长两个增长机制。
  淞附增长：在混合云中，冰晶粒子质量增长可以通过与过冷水滴的碰撞，然后过冷水滴在上面冻结起来；
  该过程称作凇附增长（碰冻增长），造成各种形状的结凇体。
  丛集增长：冰晶增长是通过冰晶相互碰撞与粘连。如果冰晶粒子下降末速度不同，它们彼此就会碰撞、粘连使得冰晶增长。
  冷云中的降水与暖云类似:最初依靠混合云中水汽凝华增长，然后通过凇结和/或丛集增长，便可在合理时间内（例如40分钟）产生降水粒子。
  降雨的机理可以用下图来综合描述：
  

4、气溶胶&云化学

在上一章云微物理学中，我们提到了云滴的重要来源便是异相核化。不论是CN还是IN，对于暖云和冷云的形成都起着重要的作用。
那么，CN与IN从何而来？在大气中，除了洁净的空气外还有什么？这些空空气中“杂质”会对地球大气造成什么影响？
这就是我们这章要介绍的——气溶胶。
气溶胶（ aerosol），指悬浮在气体中的固体和（或）液体微粒与气体载体共同组成的多相体系。相应的，大气气溶胶一词是指大气与悬浮在其中的固体和液体微粒共同组成的多相体系。
大气气溶胶是一种复杂的，多相体系，而构成这个体系的，独立于干净空气之外的液态或固态颗粒，我们称之为气溶胶粒子。
简单来讲，我们生活的大气中并不是只有干净的空气，在空气中，存在着大量的“杂质”（气溶胶粒子），这些”杂质“分散在大气中，与大气一起构成了一个混合多相体系——大气气溶胶。
我们常说的PM2.5 PM10 就属于大气气溶胶粒子。
严格来讲，我们原本就生活在大气气溶胶这个多相体系中，我们所看见的通常并不是干净的大气，而是”气溶胶“。
从这方面来讲，气溶胶对于大气的影响毫无疑问是极大的，它几乎影响了气象所能研究的各个方面：影响大气的光学特性，降低能见度；充当CN、IN影响云的生成与发展；改变大气的辐射收支平衡，影响全球变暖；捕获大气中的离子，影响大气放电；发生化学反应，直接影响人体健康……气溶胶影响的范围是如此之大，以至于对它的研究注定只能成为一个边缘性的交叉学科，因为它几乎涉及了地球大气的所有过程，涉及了经典物理学中的所有分支。
在本章中，我们只介绍气溶胶一些最基本概念：描述、源与化学组成、汇（云化学过程）以及一些简单的气溶胶的气候效应介绍。主要内容如下图：

粒度谱分布
由于自然原因与人为排放，无论是在城市还是偏远地区，大气中都含有大量浓度的气溶胶粒子，有时高达10⁷ ~10⁸cm^-3。这些粒子的直径跨度超过四个数量级，从几纳米到大约100米。燃烧产生的颗粒，如汽车、发电和木材燃烧产生的颗粒，小到几纳米，大到一米。风尘、花粉、植物碎片和海盐一般大于1米。大气中光化学过程产生的物质主要存在于小于1 m的颗粒中。这些微粒的大小不仅影响它们在大气中的寿命，还影响它们的物理和化学性质。因此，为了研究气溶胶颗粒的特性，我们首先应当发展一种数学方法，来描述气溶胶粒子的尺度分布。
气溶胶粒子的成分复杂，形状各异，我们难以直接描述一个复杂形状的物体的尺度，更难以将不同形状的的物体之间进行比较，为此，我们引入等效直径的方法来衡量粒子的尺度大小，通过等效直径我们可以忽略气溶胶的形状，将其视作球体。
实际工作中，最常用的是光学等效直径和空气动力学等效直径。在接下来的讨论中，所提到的所有对气溶胶粒子大小的分类，都是根据其空气动力学等效直径划分的。
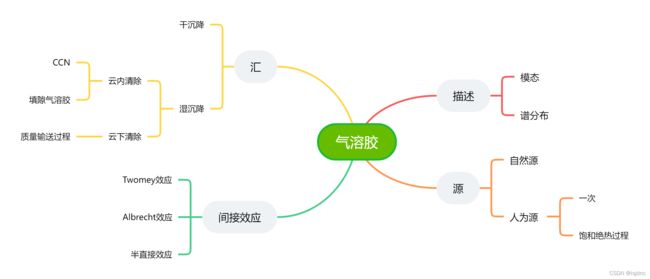
如下图，根据气溶胶尺度，将其划分为四个模态。

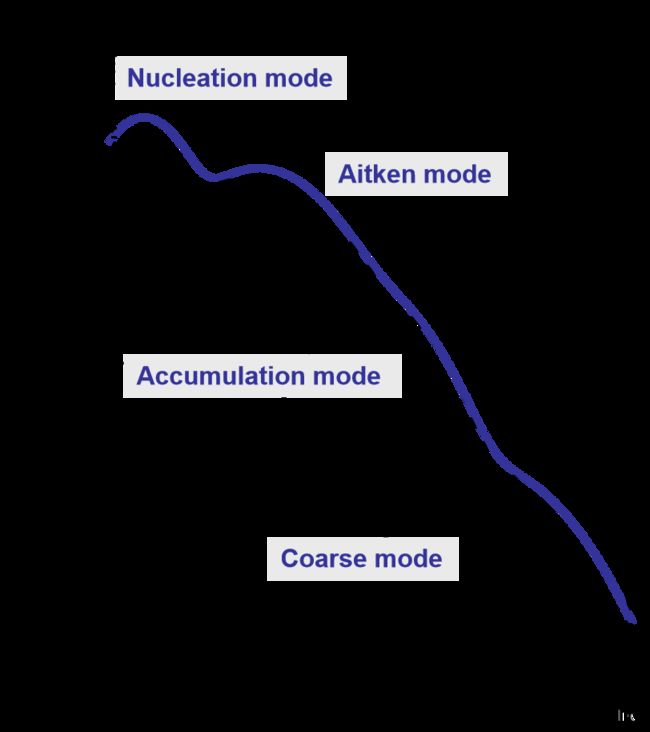
核化模态(0至20nm):气粒转换生成、人为排放排放小颗粒 (如柴油机产生的超细烟炱)
Aitken模态 (20-100nm): 气溶胶的凝结、凝聚增长.
积聚模态 (100nm-2µm):由Aitken核成长或老化颗粒. 有时双模态，由于云中发生的选择性增长.
粗模态或巨气溶胶 (D > 2 µm): 由机械产生颗粒.
通常，我们用数浓度、质量浓度、化学成分质量浓度等来描述大气中气溶胶粒子的浓度大小。
数浓度定义为单位体积空气中悬浮粒子的数目，在实际大气中，其变化范围很大。一般是将气体抽进观测仪器的计数腔内计数。
质量浓度定义为单位体积空气中气溶胶物质的质量，常用单位为毫克/米3或微克/米3。有时也用毫克/千克。
如果大气气溶胶都是由相同尺度气溶胶粒子组成，则称为单谱气溶胶或均质气溶胶，对气溶胶的一般描述使用浓度即可。然而实际中，大气中的气溶胶由多个尺度的气溶胶颗粒构成，称为多谱气溶胶。此时，仅仅知道气溶胶浓度并不能描述此时大气的气溶胶一般特征，我们需要其浓度随粒子尺度的分布，即不同尺度气溶胶在大气中的浓度，简称为粒度（尺度）谱分布。谱分布是它在大气中的输运特性、寿命及其光学特性的决定因素之一。 用一个数学公式来描述大气气溶胶的粒度谱分布，这个数学公式被称为粒度谱分布函数。
谱分布函数应当如何表示？首先，定义单位体积（1cm³)空气中，在某一时刻、体积处在v~v+dv范围中的气溶胶粒子数（数浓度）为:
dN =nN(v)dv
这里nN(v)就是以体积为特征尺度参数的气溶胶粒子数浓度谱分布函数，那么粒子总数（1cm³空气）：

对于球形粒子，直径是一个最好的特征参数，因此可定义单位体积（1cm³)空气中，在某一时刻、直径为Dp~Dp+dDp范围中的气溶胶粒子数（数浓度）为
dN =nN(Dp)dDp
这里nN(Dp)（个 μm^-1 cm^-3)就是以粒子直径为特征尺度参数的气溶胶粒子数浓度谱分布函数，那么粒子总数（1cm³空气）：

那么累积粒子数浓度谱分布函数，也就是直径小于等于Dp的粒子总数（数浓度）：

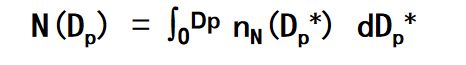
一些气溶胶的性质依赖于其表面积和体积浓度谱。定义单位体积（1cm³)空气中，在某一时刻、粒径在Dp~Dp+dDp内的气溶胶的表面积（表面积浓度）为
dS =ns(Dp)dDp
这里ns(Dp)就是气溶胶粒子表面积浓度谱分布函数（也称表面积谱分布函数），那么总表面积：

同理，也可得体积谱分布、质量谱分布定义。
由于气溶胶粒径范围跨越好几个量级，且粒径区间划分不等，在实际中，用自然对数或以10为底的对数作为独立的自变量较方便。 如nNe(lnDp), nN0(lgDp)
它们的定义前面类似，只是将自变量换位lnDp或logDp
写到这里，相信大家会觉得这些定义有些熟悉，与统计学中的PDF与CDF定义有些相像。
实际上，在描述大气气溶胶特征时，我们并不关心气溶胶粒子的特点，而是研究它的统计分布特征，用统计量来描述其一般特征，谱分布函数与统计学中的概率密度函数有着相似之处，我们可以通过谱函数的矩量来描述气溶胶谱分布的特性，这里不加赘述。
气溶胶的谱函数形式十分复杂，没有精确的函数，通常，会将整个尺度范围分成几段，利用一些经验公式来分别描述谱分布。

1. 积聚态粒子的负指数谱分布：Junge谱分布， nN0(lgDp)=CDp^-α ；式中C和α为常数（经验参数），α一般取值在2-5之间，C直接反映气溶胶的浓度。它只适用于半径大约为0.1-2微米范围的干净大气气溶胶。对城市污染大气不适用。
2. 对数正态分布
3. 粗粒子的Woodcock谱分布：一般只适用于直径大于约1微米的粗粒子范围的大气气溶胶，大于某一个特定半径的粒子总数的对数与对数半径之间有一个线性关系。
   4.┏ 分布

下图就给出了典型大气气溶胶的数浓度与体积谱分布：

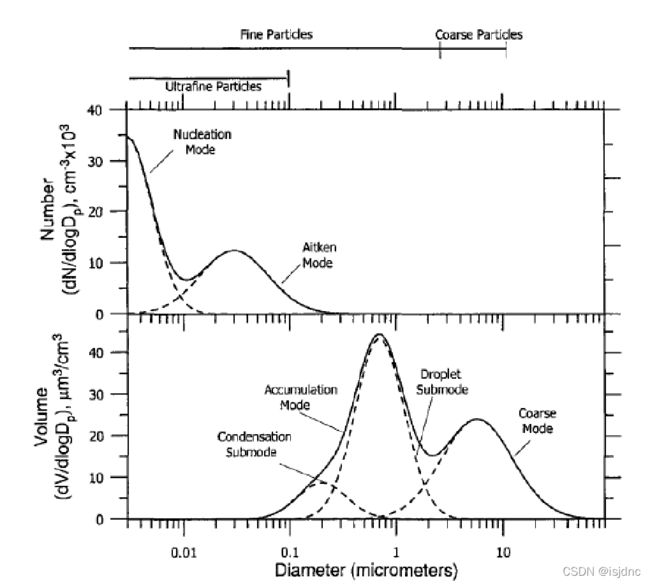
气溶胶源与化学组成
气溶胶源分为自然源与人为源。其产生主要包括二个过程：破碎和气-粒转化。自然源有火山爆发、扬尘、宇宙尘埃、海洋飞沫、孢子等；人为源主要是工业燃烧与交通运输；这些过程把粒子直接送到大气中，是大气气溶胶原生粒子的来源，
比较特殊的源是气-粒转化过程，它也是大气气溶胶粒子的重要来源，可以形成Aitken模态的气溶胶粒子，对许多大气微量成分构成了清除机制。它也就是我们在上一章中介绍的核化过程，不仅包括均相核化也包括异相核化，此处，我们不再赘述。

不同尺度的气溶胶具有不同的形成机制，在介绍气溶胶模态时我们已经给出了介绍，下图就描述了不同模态气溶胶的形成过程。

大气气溶胶的化学组成:与区域及天气条件有关。原生粒子几乎包含了自然界存在的所有元素。一般说来，海洋上空气溶胶的化学元素组成与海水的元素组成相似，干净大陆气溶胶的元素组成与地壳物质的元素组成相似。城市大气气溶胶则不但包含了地壳中丰度很高的元素，还包括了各种各样的工业污染元素。
在实际中，我们比较关心大气气溶胶中的水溶性化学元素，以及有机化合物。
大气气溶胶的水溶性离子是气溶胶的重要化学组分，其浓度与大气降水的酸度有着很密切的关系。大气气溶胶的水溶性成分主要是硫酸盐、硝酸盐和氯化物以及少量的有机酸。
气溶胶粒子中的颗粒有机物（POM)是其主要成分，约占颗粒物总质量的10%-50%。在干净大陆大气气溶胶中有机化合物的含量很低，但在城市污染大气中，颗粒态有机物种类非常繁多。颗粒有机物主要存在在粒径小的颗粒中，多数分布在0.1-5 μm内，其中55%-70%在粒径小于2μm,即属于细粒子。
大气中的有机气溶胶成分，主要通过有机碳（OC）来测量，部分由源直接排放（一次OC），部分由烃光化氧化生成的低挥发性物原位凝结而成（二次OC）。
二次有机气溶胶（SOA）的形成也是大气气溶胶的来源之一，只不过过程比较复杂，它主要通过可挥发性有机物（VOC）在大气中氧化生成，大气中SOA形成可分为三步过程：
（1）母体VOC的气相化学反应生成SOA化合物；（2）SOA化合物气相与粒相的分配；
（3）粒相反应把SOA物种转变成其他化合物。
气溶胶的汇/云化学
气溶胶的汇主要包括干沉降与湿沉降过程。
干沉降：在没有降水的条件下，通过重力沉降作用和湍流输送作用将大气微量成分（气溶胶粒子和微量气体）直接送到地球表面使之从大气中消失的过程。主要机制为：重力沉降与湍流扩散。
干沉降速率不仅取决于气溶胶本身的属性（粒子大小，形状，密度），还取决于大气的属性（如大气的温度结构，气压场，湿度场和大气稳定度）和地表特征（植被状况，地表分布等），地表特征通常用摩擦速度和空气动力学粗糙度长度来表示。
干沉降与大气边界层物理学密切相关，边界层物理是目前大气物理学的难点之一，在大气物理学这门课中对边界层物理学内容介绍较少，这里我们不多加赘述。
湿沉降，物质被大气水凝物（云滴、雾滴、雨、雪）清除并最终被送到地面的自然过程。包括降水清除、湿去除、雨冲刷（rainout)和水冲刷（washout)。
我们可以将湿沉降分为两部分：云内清除（核化）与云下清除（冲刷），它的概念图如下：

显然，湿沉降与云和降水密切相关，涉及到大量的云化学过程。下面，我们分别介绍云内与云下清除过程。
云下清除
所谓云下清除，就是大气降水将气溶胶粒子带进水中，一起下落至地表，达到清除效果。
在这个过程中，最重要的就是大气物种溶于液相中发生的质量输送过程：
1 反应物从气相扩散到气-水界面
2 物种穿过界面
3 在液相中物种可能发生水解/电离过程
4 液滴中离子或非离子物种的液相扩散
5 液相中的化学反应

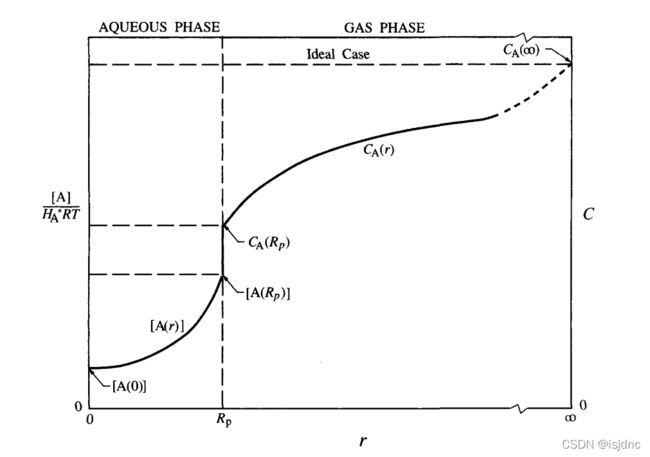
液相大气反应的反应物从气相经过一系列质量输送过程转移到云滴内部，制约质量输送的有气相中、气-水界面和液相中质量输送速率等。如果没有质量输送限制，气-液相一直保持Henry定律平衡。
这个过程速度很快，可将其视为稳态。
可溶气体或粒子进入云下雨滴,物种i的清除速率近似地可用以下的一级关系表达:

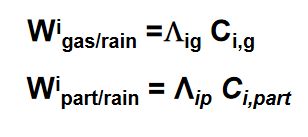
Λig and Λip 是物种i在气相和颗粒相的清除系数。
如果在一个水平均匀的大气中物种i的浓度为Cg(z,t),那么其云下清除速率（通量单位）为：

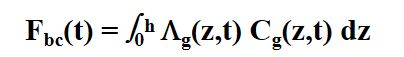
h为云底高度。
云内清除
云中吸收的气溶胶物质（或气体）随雨滴降落到地面而完成清除过程。
气溶胶云中清除是2个过程的结果。首先，成核清除（云凝结核（CCN)生长到云滴），然后剩下一部分气溶胶被云滴或雨滴收集。
所谓云内清除，就是指气溶胶作为云凝结核被活化，异相核化产生新粒子，再经过增长、凝聚等微物理过程清除。
云内清除的效率并不高，然而，却对云的物理化学特性有极大的影响。
云凝结核
在某一过饱和度条件下能够活化的颗粒定义为该过饱和度的云凝结核（CCN）。
在云物理文献中，凝结核（CN）通常定义为过饱和度>400%条件下形成云滴的颗粒，因此CN包括所有颗粒。因此，可认为CN浓度等于总气溶胶数浓度。
CCN浓度通常对应特定的过饱和度，例如CCN(1%)或CCN(0.5%)指不同过饱和度条件下测得的CCN浓度。 我们用CCN(s)表示s%过饱和度条件下的CCN。
某一给定的气溶胶群，CCN(s)既依赖于粒子尺度，又依赖于成分。对于一个简单的例子，即假定气溶胶成分不依赖于粒径，根据定义则有：

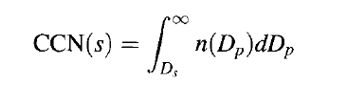
其中n(Dp)是气溶胶群的数浓度分布，Ds是这些粒子在s%过饱和度条件下的活化直径。
核化清除
云内气溶胶核化清除是指部分气溶胶活化、继而增长变成云滴的过程。
如果在云形成之前（例如在云底）气溶胶成分的密度为Ci,0， Ci,cloud 和Ci,int 分别是其水相和填隙气溶胶的密度，则可定义成分 i 的云清除质量比为Fi，

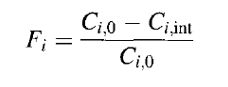
如果云内没有成分 i 生成或去除，则Ci,0 = Ci,int + Ci,cloud。质量清除比范围为0~1
数量清除比可定义为FN：

其中N0是云形成前气溶胶的数浓度，Nint是填隙气溶胶的数浓度。
理论上，因为粒径大于0.5μm的粒子成为云滴，而且这些粒子占到了气溶胶质量的大部分，因此质量活化效率近似于1。大量理论研究表明，对于所有气溶胶成分，质量核化清除效率都很高，0.5~1。
相反，云中气溶胶数量清除效率很低，主要受到人为源的影响（气溶胶细颗粒）。在大多数情况下，数量清除效率仅有百分之几或更小；只有在偏远的海洋大气中，总数量清除效率超过0.1。
云内部分气溶胶粒子核化成云滴被清除，而剩余部分作为填隙气溶胶存在。填隙气溶胶可以通过与云滴碰撞后从云填隙空气中去除，这些颗粒通过布朗扩散被云滴捕获。
核化清除效率对化学成分依赖性比较复杂，主要影响因素包括：化合物的多样性、粒径大小不一。

冷云降水化学
气溶胶的湿沉降过程可以将大气物种迁移至较大粒径的降水的粒子中，我们上面已经简单介绍了气溶胶粒子在云中与云下的清除过程。在暖云中，挥发性物质在碰并过程可能被排出，出现化学平衡的偏移，对于非挥发性物质简单相加合并即可。
但对于冷云过程而言，由于冰相的特殊性质与相变过程，化学物质的升尺度迁移更加复杂。
上一章我们介绍了冷云过程，冰晶通过三种方式增长：凝华增长、淞附增长、丛集增长。
对于冰晶的丛集增长由于纯净的冰晶所含化学物质量极少，故该过程在微化学计算中通常忽略。
对于淞附过程，过程复杂一些：
对于非挥发性溶质，在冰粒子与过冷水的凇结过程中，捕获过程与碰并增长并无不同；但是，当被捕获水滴冻结时，像硫酸盐这样的溶质将被排斥于冰晶格之外，而被挤进小容积液滴，但是仍被凇结粒子携带。所以，凇结过程对于非挥发性溶质由小向大粒子迁移是有效的。
然而，对于挥发性溶质，凇结过程有很大不同。当挥发性气体浓度超过水相中Henry定律平衡值时，则被吸收成为溶质；但如果小于平衡值浓度，则该溶质解吸出来，恢复成气态。凇结就是一个可以导致后者的过程。
对于凝华增长过程：随着过冷水滴的蒸发，其中的溶质浓度增加。挥发性溶质被解吸出来，释放溶解气体返回空气。非挥发性溶质不会解吸，仍保留在逐渐缩减的液滴中，直至完全蒸发成为填隙气溶胶。所以，过冷水滴中溶质不会直接转移到较大粒子中去。
因此，水汽凝华增长充当低温蒸馏过程，阻止化学物质的升尺度迁移。
这也是雪比霰粒子干净的原因，因为雪是由凝华增长生成，而霰粒子则由淞附过程产生。
气溶胶的间接效应
直接效应：
气溶胶可以通过散射和吸收地面长波和太阳辐射短波对地气系统产生影响。
间接效应：气溶胶参与并影响云降水形成过程。气溶胶可以作为云凝结核（CCN）参与到云的生成、演化和消散过程，改变云滴大小、云的微物理结构及其光学特性，从而影响云的生命期及降水效率。
间接效应分为两种：
第一间接效应(i.e.,Twomey效应、云反射效应)：
由于人为气溶胶的增加导致云滴数浓度增加，云滴半径减小，导致云的反射率增加。
第二间接效应(i.e.,Albrecht效应、云生命期效应)：
气溶胶增加导致云滴粒径减小，从而调整了液态含水量和云的厚度，降低了降水效率从而增加了云的生命期。
半直接效应：部分气溶胶（烟炱等）会吸收太阳辐射导致空气增暖，会导致云滴蒸发。
当云之上存在吸收性气溶胶层时，有可能出现另一个半直接效应：
云上加热增强稳定度，减少云顶湍流混合（即云顶夹卷），延长云的生命期。
此外，气溶胶对降水也有影响。
增益 (Invigoration) 效应：气溶胶增多造成CCN变多，对流云早期更多数量、更小云滴，无法形成有效降水。小云滴爬得更高、更多到达更冷的高度。如果它们到达冻结高度，云滴冷冻变成冰粒子，释放潜热，增加浮力，云长得更高并最终发展成雷暴。
注意：若云底已在0℃以上高度，则云中大多数水已经冻结，降水不会增强。

5、大气辐射学基础

近年来，“全球变暖”成为了重要议题，我们都知道全球温度在过去几十年间异常升高，可是，升高的原理是什么？
我们不妨在把问题拉远、拉宽一些：为什么地球会有相对其他星球更加适宜的温度？为什么会演化出生命？为什么大气会运动？为什么生命能够生长？
上述的所有问题，都需要能量来维持，那么地球能量的最终来源是什么？
每个人都能给出回答：“太阳”。
没错，太阳提供了最基础的能量，太阳的能量是通过什么传输到地球呢？
通过“光”，也就是我们这章所讲的“辐射”，我们可以将它简单理解为一种传输能量的方式。
太阳辐射是大气运动的能源，辐射过程是地-气系统中能量交换的主要过程，大气辐射学，就是研究地球大气与太阳辐射之间的辐射传输与转换过程的学科。在一章，主要介绍基本辐射原理、辐射过程，给出地球大气的一些基本辐射模型、一些辐射强迫效应等。

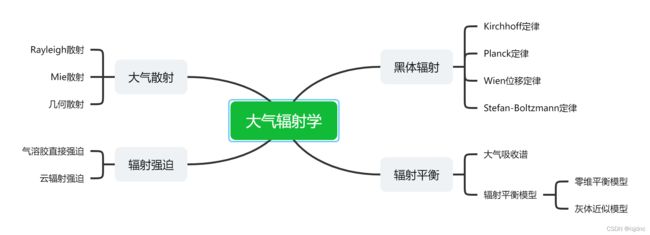
基础知识
电磁辐射可以看作以光速传播的波的集合。它的特征可以通过波长λ、频率ṽ、波数v描述。
在研究辐射传输时，根据波长大小，一般将其划分为以下几类：

辐射传输具有方向，也具有大小。为了定量描述辐射传输的强度和方向，我们一般定义以下物理量：
首先，地球是一个三维球体，想要定义辐射在球体中的传播方向，我们通常采用立体角的概念。
在研究地球大气时，为了研究不同的问题，通常会采用不同的坐标系。在研究地球辐射传输，采用球坐标系。
球坐标中，每一个方向可以用两个角来表示，方位角、仰角。这两个角定义了球中惟一的方向Θ(φ,θ)。

立体角是以圆锥体的顶点为心，半径为r的球面被锥面所截得的面积来度量的，度量单位为“球面度”（steradian，符号∶sr）。球面度表示为三维弧度。
半球上的立体角定义为覆盖半球表面区域的面积除以半径的平方：


为此，我们有了下列定义：
辐亮度：单位面积、单位时间、单位波长与单位立体角上通过的辐射量，它也称为单色辐射率，因为只考虑了单位波长范围内的辐射大小。
辐射通量：单位时间通过某一平面的辐射能。
辐射通量密度（辐照度）：辐射场内任一点通过单位面积的辐射通量。可由辐亮度计算：

当辐射强度为各向同性，则

称为朗伯定律，满足这个条件的辐射体称为朗伯体，在一般情况下，太阳可以看作朗伯体。
黑体辐射
当一个辐射入射至某个物体时，辐射有三种去向：被物体吸收、透射、散射。
根据能量守恒，有Q0 = Qa + Qr + Qt，可定义吸收率A = Qa/Q0、反射率R = Qr/Q0、透射率τ = Qt/Q0 ；显然，A + R + τ = 1。
吸收率、反射率、透射率的概念可应用于各种波长称为单色吸收率Aλ、单色反射率Rλ、单色透射率τλ。
如果某一物体对任何波长的辐射都全部吸收，即吸收率A = 1，则称该物体为绝对黑体，即R = τ = 0
如果物体仅对某一波长λ全部吸收，即Aλ=1，则该物体对这一波长为黑体。
若物体的吸收率A不随波长而变，且A<1，则该物体称为灰体。例如：地面对长波辐射的吸收率近于常数，可认为地面为灰体，且吸收率接近于1。
下面介绍有关黑体辐射的四大定律；
Kirchhoff定律
在热力学平衡的条件下，各种不同物体对相同波长的单色辐射出射度与单色吸收比之比值都相等，并等于该温度下黑体对同一波长的单色辐射出射度。
即物体发射率＝吸收率
发射率一个给定表面所发射的功率与同一特征的黑体所发射的功率之比，是波长的函数。对于地球大气60km以下，该定律都成立。
Planck定律
普朗克通过实验，确定了温度为T的黑体发出的辐亮度为：

c1 ＝ 3.74 ×10^-16 W/m2 and c2 ＝ 1.45 ×10^ -2^ m/K.

上图是不同温度黑体发射的不同波长的辐照度图，我们可以看到，将每一个曲线的极大值连接起来，似乎满足着某种线性关系。这就是接下来要介绍的Wien位移定律。
Wien位移定律
B(λ,T)在某一波长存在峰值； 对Planck方程求偏微分，可得到温度为T时黑体最大辐射波长:

温度增大时，λm减小；峰值辐亮度与温度的五次方成正比。
通过此定律，我们可以计算出物体的色温。
Stefan-Boltzmann 定律
在整个波段对Planck方程积分，得到黑体总辐射通量密度（辐射度）：

其中σ是Stefan-Boltzmann常数，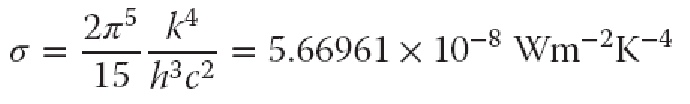
根据总辐射度，得到等效黑体温度（或有效发射温度）T_E。
大气吸收谱
大气中各种气体成分对于辐射具有选择性吸收的特性，这是由组成大气的分子和原子结构及其运动状态决定的。
气体分子或原子内的电子能级跃迁，原子和分子的振动、转动能级跃迁等，所发射和吸收的辐射谱是非连续性的，由分离的谱线和谱带组成，构成原子的线光谱和分子的带光谱。
电子能级跃迁形式主要有三种：

然而，由于一些作用，吸收谱存在加宽，主要有两种机制：多普勒加宽和压致加宽。
压致加宽：分子间不断碰撞引起的谱线加宽。一个理想振子仅有一个频率，且以此频率一直保持振动。但是，如果该振子时而受到干扰，则谱宽增加。Lorentz 认为分子间的碰撞干扰吸收与发射，吸收谱宽受到碰撞间隔的控制。
压致加宽的线性因子为Lorentz线性因子：

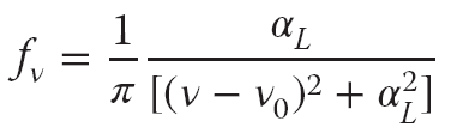
其中，a_L为Lorentz半宽度，通常根据分子碰撞平均间隔时间估计：

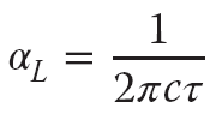
Doppler加宽当气压很低时，分子速度对线形有重要影响。根据分子的速度，吸收或发射光的波数产生Doppler偏移，偏移值为：

V为分子速度，与光传播方向相反取正，相同则取负。
此外，对于波长较小的紫外辐射，它们的吸收主要受光致电离与光解作用。
光致电离：波长小于0.1μm的极紫外辐射，其能量足以剥夺原子的电子。该波段太阳辐射在大气层90km高度以上的电离层被吸收，产生大量的自由电子。
光解作用：波长小于0.24 μm的紫外辐射把O2分子分解成氧原子；波长小于0.31 μm的紫外辐射把O3分子分解。
在光致电离、光解反应中，这些光子被吸收，多余能量转变成分子动能，加热大气。
大气的主要吸收谱如下：

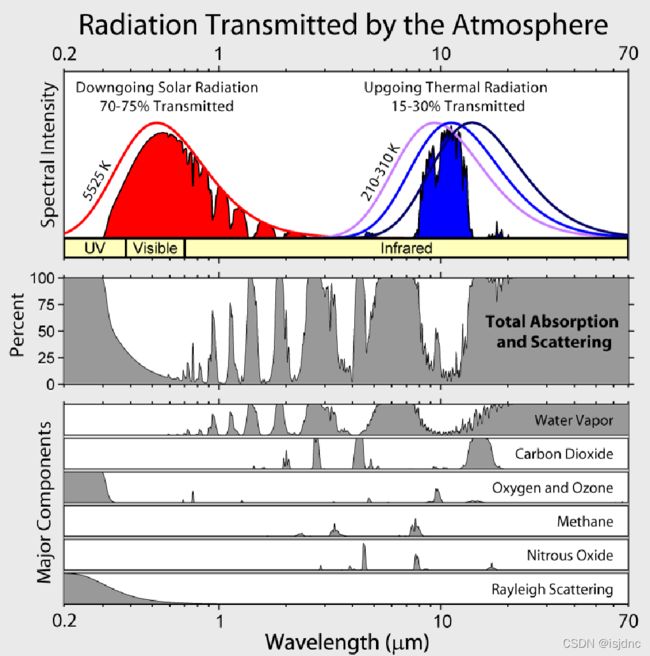
根据大气对于太阳辐射的吸收特点，我们可以发现大气对8-12μm波长吸收很弱，这一部分我们称为大气窗区。
辐射平衡模型
在介绍辐射平衡时，我们应当首先弄清楚：辐射模型的主体是什么？它们有什么特点？有哪些过程？受那些影响？
最基本的过程描述是：太阳发射辐射，到达地球大气顶端，经过一系列过程（散射、吸收），最终，部分辐射到达地球表面，地表增温。
然而：地球同样具有温度，也可以同样发射辐射至大气，再经过散射、吸收等过程，透过大气窗区发射到宇宙中。
这中间自然存在着一个辐射平衡的问题，据此，我们可以建立一系列辐射平衡模型。但再开始之前，我们需要简单了解，两个主要辐射体所发射辐射的特点。
太阳辐射：太阳主要发射在0.3~3μm波长的短波辐射；它们主要被大气中的：H2O、O3、O2、CO2等吸收。

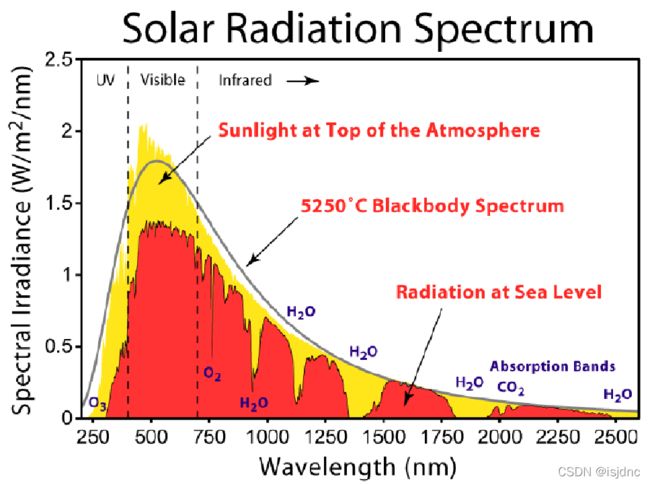
地球辐射：地球表面发射的能量主要位于3-30μm 波长的长波辐射，主要被大气中的H2O和CO吸收，近年来，由于人类活动造成的其他温室气体对于长波波段的吸收增加也不可忽视。

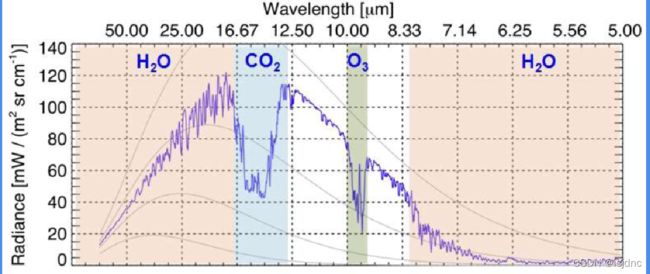
下图给出了地表与大气之间的能量平衡过程（全球尺度，未考虑下垫面）：

下面开始介绍辐射平衡模型，先考虑最简单的零维辐射平衡模式。
设想一个最简单的情况：假如，地球没有大气作用，太阳辐射入射到地球表面，部分被地表反射，部分透射出去，而剩余被吸收，用来加热地球。那么，此时的地球平衡温度会是多少？

我们可以很简单的写出能量平衡公式：

Q0为太阳常数，定义为在平均太阳距离大气外垂直于太阳光线的单位面积上单位时间内接受来自太阳的能量，一般取S = 1368 w/m2,α则为地球行星反照率，一般等于0.3。
为此，我们可以计算出在没有大气的情况下，地球辐射平衡温度为255K（-18℃），这显然与实际不符。
而之所以会这样，便是我们忽略了大气的增温作用，即，温室强迫引起的地球增温。
如果将大气考虑进来，情况会如何？为此，继续提出了灰体窗近似模型。
我们有如下的假定：大气为黑体，对于太阳光透明，均匀吸收红外辐射，不随波长变化；大气为等温大气；吸收率=发射率ε。
灰体窗近似模型基本过程表示如下：

可以看出：

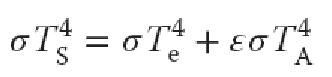
地表温度＞零维模型计算的地球辐射平衡温度。
该模型并不适用于对流层，需要考虑对流过程对其调整。
通过上述解释，我们也能明白温室气体的增加为何能够促使全球变暖：
首先，温室气体的增加使得大气吸收了更多的长波辐射，这样，就使得在长波波段，地球向外发射的长波辐射能量降低。
然而，能量永远是平衡的，此消彼长，为了达到新的能量平衡，地球在其他波段的能量发射必然要增加。
此时，尽管地球发射的总能量依然平衡，但原本应该被发射出去的能量减少，最终地球被加热。
大气散射
散射：由于辐射与分子、粒子的相互作用，从而导致辐射传播方向的重新分布。散射形式：反射、折射、衍射（绕射）等。
在大气中，除去气体对于太阳辐射的吸收与散射作用外，气溶胶粒子对于辐射的散射与吸收作用也十分重要（气溶胶的直接效应）。
大气散射与我们的生活息息相关，在日常生活中的不少问题，都可以用大气散射的知识来解释。
散射类型
粒子对光的散射机制可分为以下三类：
弹性散射 — 散射光波长（频率）与入射光波长相同为λ0 （Rayleigh与Mie散射）（不是分子内在的振动频率）。
准弹性散射 — 由于Doppler效应（注：不同于吸收线加宽）和扩散增宽引起波长（频率）漂移。
非弹性散射 — 发射辐射与入射辐射波长不同（Raman散射（包括Stokes散射与反Stokes散射）、荧光性，比较复杂 ） 。
通常情况下，我们只考虑弹性散射，根据粒子与空气分子的相对尺度χ：分为三类：

χ<< 1: Rayleigh散射（与波长相比粒子很小）
χ~ 1 : Mie散射（粒子大小与波长相当）
χ>>1 : 几何散射（与波长相比粒子很大）

Rayleigh散射
当散射粒子远小于光的波长时，该过程称作Rayleigh散射。
远小于光波长的颗粒在所有方向都散射光。它们的散射于波长的四次方成反比。
可见光的空气分子散射为Rayleigh散射，它可用来解释：晴天天空为什么是蓝色？为什么日出太阳是红色？为何水平线上天空发白。
Mie散射
相比于空气分子和小粒子散射，大的沙尘颗粒与悬浮水滴的散射方式有很大的不同，它们叫做米散射；它们不产生红色太阳，而只是使太阳变得暗淡。
与Rayleigh散射相比较，米散射对光波长的依赖性很小，它可以解释云为什么是白色。
大气消光
当一束光撞击一个粒子时，粒子中的电荷被激发进入振动状态；激发态电荷在所有方向再发射能量（散射），或者把部分入射辐射转变成热能（吸收）。
为了定义粒子的吸收和散射能力，我们给出了散射截面和吸收截面。
假定入射辐射强度为F0（W/m2），一个粒子散射能量正比于入射强度，即
其中Cscat (m2)为单粒子散射截面，
同理有：

其中Cabs (m2)是单粒子吸收截面。
根据能量守恒，入射光等于粒子在所有方向散射光与粒子吸收光之和。散射和吸收的联合效应称为消光，消光截面(Cext)可定义为：

粒子的散射效率 Qscat是一个无量纲数 Cscat /A，其中A是粒子的截面积。 同样可定义吸收效率Qabs和消光效率Qext：

Qscat与Qext之比叫做单次散射反照率（SSA）

为了衡量大气消光作用，我们定义光学厚度τ，定义为：单位截面积上吸收和散射物质产生的总衰弱。
对于某一层气溶胶，光学厚度为τ，对于穿过该层气溶胶的辐射，其透射部分为e^–τ。
根据光学厚度与散射比定义，我们可以构建气溶胶散射吸收模型。
气溶胶直接强迫
气溶胶可直接通过散射和吸收太阳辐射影响气候，又可以通过影响云的特性起到间接效应。
对直接效应而言，气溶胶可以散射辐射，又可以吸收辐射，而吸收与散射作用的强度比较，决定了气溶胶起着冷却效应还是增温效应。
构建气溶胶的吸收散射模型，考虑太阳光入射气溶胶层，入射光太阳天顶角θ0 = 0°。透射气溶胶层的部分为e^–τ，τ为该层光学厚度；
则散射+吸收= 1-e^–τ， 其中吸收与散射部分为(1–ω)(1– e^–τ)、ω(1– e^–τ)
反射部分为r = (1–e^–τ)ωβ，ω为单次散射反照率，β为向上的散射部分 。
那么，总的向下透射为：

如果地表反照率为Rs，则地表反射部分为 tR。

然而，地表向上反射的RstF0进入气溶胶层，部分后向散射回地球，部分向上散射，散射回地球的部分再次经过上述过程，如此反复，有：

根据等比数列求和，我们可以将其写作：

为总的向上反射通量。括号中的量为气溶胶-地表系统的总反射率，可用符号Ras表示:

那么，气溶胶层的直接效应究竟是冷却还是加热，u决定于Ras和地表反照率的关系。

ΔRP符号决定气溶胶强迫是负（冷却效应）还是正（加热效应） 。关键控制参数是单次散射反照率 ω 。气溶胶是散射还是吸收特征可以通过SSA值的测量。
粒子吸收能否导致行星反照率的增加还是降低，依赖于粒子SSA，也依赖于地表反照率。 在暗地表上空（如海洋），粒子趋向于增加行星反照率，因为气溶胶层的向上散射超过暗地表的散射。而在高反照率地表上空（如雪或明亮的沙漠），粒子吸收可以减少地表的太阳发射通量，从而导致返回太空的净辐射减少。
云的辐射强迫
云对太阳辐射的强迫作用十分重要，也是气候变化研究最优先领域，因为云是未来气候变化预测不确定性最大的源。
不同类型的云有着不同的物理光学特性，其对辐射的强迫作用也不同。

它有两种强迫作用:
云反照率强迫：太阳短波辐射在云中散射，很多辐射返回太空。云反照率强迫将导致地球变冷。
云温室强迫：当云吸收地表长波辐射时，云再发射能量，部分向太空、部分返回地表。该过程称作“云温室强迫” ，导致地球气候变暖。
云是全球反照率的主要控制因子，所有云的总体起着冷却效应；但在不同的时空尺度上会有所不同。
云对地球辐射平衡的效应决定于晴空(clear-sky)与全天空辐射之间的差异：

负FNet(云) →云对气候冷却效应
正FNet(云) →云对气候有增温效应
对于云对辐射作用，至今仍有许多不确定性，对于真实大气的观测十分重要。

结语

相比起大气动力学、天气学课程，大气物理学这门课程涉及了太多的研究内容与挑战，几乎每一个分支都可以开专门的课程来讲授，严格来讲，它可以看作几个大气研究方向的综合。
这就会导致一个问题：每一章的内容似乎都相对独立，学生只要选择一个相应的分支与学习就好了，为什么要将所有的学科基础知识都过一遍呢？
我的答案是：虽然每一章的内容相对独立，但其实在细节处都有着相互连接的地方，比如说云滴的形成涉及到大气热力学中所讲述的绝热过程、大气辐射中的云的辐射强迫十分重要等等，清记住，我们的大气是一个整体，任何物理现象都不可能完全独立存在。
写这篇笔记的起因，是我在复习过程中发现了自己一直以来最大的缺陷：浮于表面，不成系统。
自然科学的研究都要有极为坚实的理论作为基础，没有这些，连基本的问题都无法理解和发现，模式也是如此，将精力与能力放在代码编写、跑动模式、数据处理与绘图中，就算再好也只是个花架子。当我阅读文献综述，进行复习时，这样的感觉愈发深刻。
我知道大气热力学的干湿绝热过程，却不明白考虑”绝热过程“本身的意义在哪里；我可以机械地背出暖云中云滴的两种增长机制，却不明白它们的关系与对云的影响；我能不假思索地背出气溶胶的源汇项和模态，可从未想过它们对研究气溶胶究竟有什么作用；就连似乎最熟悉的大气辐射基础，我之前都没有真正将云的辐射强迫考虑进去（之前仅仅只有一个印象）。
这让我感到惶恐和羞愧。
于是我起了：”将比较重要知识点自己梳理一遍，说不定能有懂得多一点。“的想法，开始动手写这篇博客笔记，
写的过程并不让人舒适，事实上，当它写完时，大气物理考试已经结束三周了，为此还占用了我其他考试的复习与文献阅读时间，这似乎得不偿失。而我被一种奇怪的执念督促，还是勉强将其完成。
写完以后并没有太多的满足，而是更大的羞愧，我应该比之前了解得更深了，可我显得更加无知。
那么，收获是什么呢？
我想，是对于我所研究，这个复杂、混沌、神秘的系统的敬畏吧。
仰止弥高，钻之弥坚。
在研一这个还未正式开展科研工作的时期，能够潜心梳理理论知识，或许这也是种幸运，是我所喜爱的“无用却有趣”的事情，大概这就够了。