python中dot函数总结

本文结合其他博主的一些介绍总结了dot函数运算过程

基本简介

dot函数为numpy库下的一个函数，主要用于矩阵的乘法运算，其中包括：向量内积、多维矩阵乘法和矩阵与向量的乘法。

1. 向量内积

向量其实是一维的矩阵，两个向量进行内积运算时，需要保证两个向量包含的元素个数是相同的。

例1：

import numpy as np

x = np.array([1, 2, 3, 4, 5, 6, 7])

y = np.array([2, 3, 4, 5, 6, 7, 8])

result = np.dot(x, y)

print(result)

输出结果：

168

计算过程就是将向量中对应元素相乘，再相加所得。即普通的向量乘法运算。

2. 矩阵乘法运算

注意：

1.数组的运算是元素级的，数组相乘的结果是各对应元素的积组成的数组，而对于矩阵而言，需要求的是点积

2.两个矩阵(x, y)如果可以进行乘法运算，需要满足以下条件：

   x为 m×n 阶矩阵，y为 n×p 阶矩阵，

   则相乘的结果 result 为 m×p 阶矩阵。例子如下

例2：

import numpy as np

x = np.array([[1, 2, 3],

[3, 4, 4]])

y = np.array([[0, 1, 1, 1],

[1, 2, 0, 1],

[0, 0, 2, 1]])

result = np.dot(x, y)

print(result)

print("x阶数：" + str(x.shape))

print("y阶数：" + str(y.shape))

print("result阶数：" + str(result.shape))

结果为：

[[ 2 5 7 6]

[ 4 11 11 11]]

x阶数：(2, 3)

y阶数：(3, 4)

result阶数：(2, 4)

下面我们来分析一下一维数组到多维数组之间的运算过程

2.1如下单个数的dot函数运算所示：

np.dot(5,8)
40

2.2如下一维数组的dot函数运算所示：

#如果arr1和arr2都是一维数组，那么它返回的就是向量的内积

arr1=np.array([2,3])

arr2=np.array([4,5])

np.dot(arr1,arr2)

#23

如图所示： 

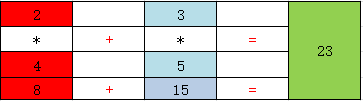
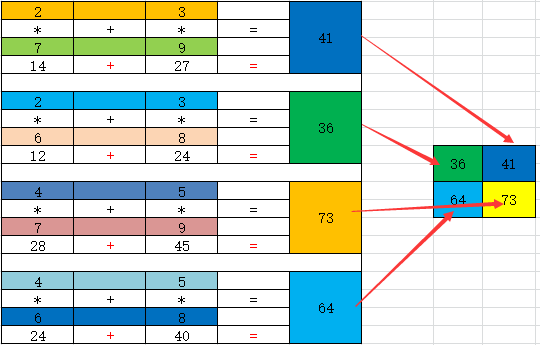
2.3如下二维数组的dot函数运算所示：

#如果arr5 和arr6都是二维数组，那么它返回的是矩阵乘法

arr5=np.array([[2,3],[4,5]])

arr6=np.array([[6,7],[8,9]])

np.dot(arr5,arr6)

"""

array([36,4],

          [64,73])

"""

运算过程如下所示： 

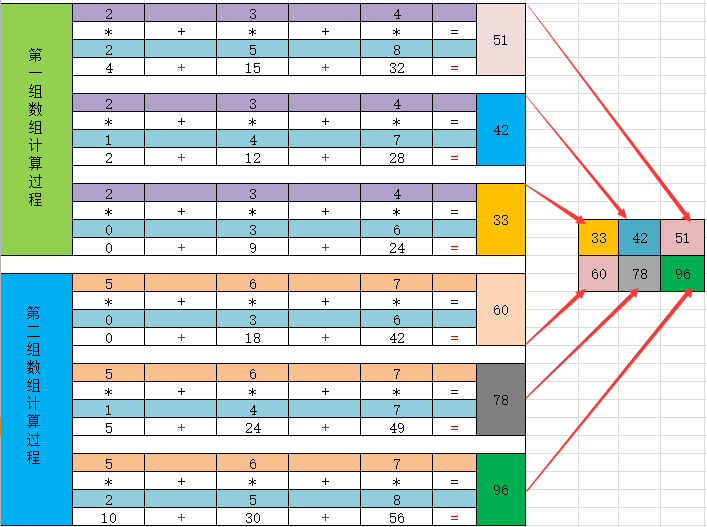
2.4如下二维数组与三维数组的dot函数运算：

#arr7二维数组与arr8三维数组的dot函数矩阵运算

arr7=np.array([[2,3,4],[5,6,7]])

arr8=np.array([[0,1,2],[3,4,5],[6,7,8]])

np.dot(arr7,arr8)

"""

array([33,42,51],[60,78,96])

"""

 

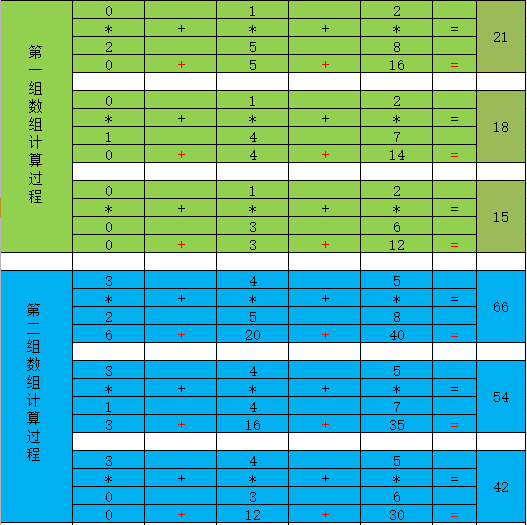
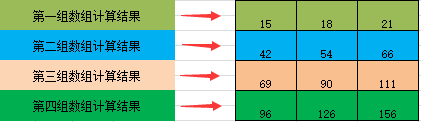
2.5如下多维数组的dot函数运算所示：

#多维数组的dot函数矩阵运算

arr12=np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])

arr13=np.array([[0,1,2],[3,4,5],[6,7,8]])

np.dot(arr12,arr13)

"""

array([15,18,21],

        [42,54,66],

        [69,90,111],

        [96,126,156])

"""

注意：

dot()函数可以通过NumPy库调用，也可以由数组实例对象进行调用。例如：a.dot(b) 与 np.dot(a,b)效果相同。但矩阵积计算不遵循交换律,np.dot(a,b) 和 np.dot(b,a) 得到的结果是不一样的。