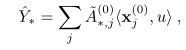FEW-SHOT LEARNING WITH GRAPH NEURAL NETWORKS翻译

基于GNN的小样本学习

简介：

我们提出利用基于推理的图模型来研究小样本学习问题，输入图像有标签或者隐藏标签。通过使用消息传播算法，我们定义了一种图神经网络来概述最近提出的几种小样本学习的模型。除了提高数值性能之外，我们的框架还可以轻松扩展到少数学习的变体，例如半监督学习或主动学习，这证明了基于图的模型能够很好地处理“关系”任务。

介绍:

监督端到端学习是在CV,speech,机器翻译任务中是非常成功的，得益于优化技术的改进，更大的数据集以及深度卷积或递归架构的简化设计。 尽管取得了这些成功，但是这种学习设置并未涵盖许多仍然可以实现和期望学习的方面。
例如能通过少量样本学习的方式，few shot 学习任务。 研究人员没有依靠正则化来弥补数据的不足，而是在人类学习的启发下，探索了利用相似任务分布的方法。 （2015）。 这定义了一种新的监督学习设置（也称为“元学习”），其中输入/输出对不再由图像的iid样本及其相关标签给出，而由图像集合的iid样本及其相关标签相似性给出。
最近一项非常成功的研究程序已将这种元学习范式用于few-shot 图像分类任务。从本质上讲，这些工作学习了一种上下文相关的，针对特定任务的相似性度量，该度量首先使用CNN嵌入输入图像，然后再学习如何组合集合中的嵌入图像以将标签信息传播到目标图像。
特别是，将few-shot学习问题作为监督分类任务，将一组图像支持集(support set)映射到所需标签中，并开发了一种端到端体系结构，接受这些支持集作为通过注意机制的输入。 在这项工作中，我们以此工作为基础，并认为该任务自然地表示为图上的监督插值问题，其中节点与集合中的图像相关联，并且边缘由可训练的相似性内核给出。 利用图结构化数据表示学习的最新进展.因此，我们提出了一个基于图的简单实现学习模型，该模型实现了任务驱动的消息传递算法。 最终的架构经过端到端的培训，捕获了任务的不变性，例如输入集合中的排列，并在简单性，通用性，性能和样本复杂性之间提供了良好的折衷。
除了few-shot学习之外，一项相关的任务是能够从带标签和未带标签的示例中进行学习-半监督学习和主动学习，其中学习器会要求这些没有标签的数据能帮助预测任务更好。 我们基于图的体系结构自然可以扩展到这些设置，而训练设计的更改却很少。 我们在少量图像分类上实验性地验证了该模型，以更少的参数匹配了最新技术的性能，并演示了在半监督和主动学习设置中的应用。
贡献如下：
.我们将短时学习作为一种有监督的消息传递任务，该任务使用图神经网络进行了端到端的培训。
•我们用更少的参数匹配了Omniglot和Mini Imagenet任务的最新性能。
•我们在半监督和主动学习机制中扩展了模型.
本文的其余部分的结构如下。 第2节介绍相关工作，第3、4和5节介绍问题的设置，我们的图神经网络模型和培训，以及第6节的报告数值实验。

2.相关工作

Fei-Fei等人首先介绍了one-shot。 （2006年），他们假设当只有一个或几个标签可用时，当前学习的课程可以帮助对新课程进行预测。最近，Lake等人。 （2015年）提出了一种分层贝叶斯模型，该模型在几次镜头学习字母识别任务中达到了人类水平的错误。
从那时起，one-shot学习取得了长足的进步。 Koch等。 （2015年）提出了一种基于深度学习模型，该模型基于使用暹罗网络计算样本之间的成对距离，然后，该学习距离可用于通过k近邻分类来解决one-shot问题。 Vinyals等。 （2016）提出了使用余弦距离的端到端可训练k最近邻，他们还引入了一种使用注意力LSTM模型的上下文机制，该机制在计算两两距离be时考虑了子集T的所有样本补间样本。 Snell等。 （2017）扩展了Vinyals等人的工作。 （2016年），通过使用欧氏距离代替余弦值，余弦值得到了显着改善，他们还为少数学习场景建立了每个班级的原型表示。 Mehrotra＆Dukkipati（2017）训练了一个深层残差网络以及一个生成模型，以近似估计样本之间的成对距离。
一种用于近期新型的one-shot学习升起：Ravi＆Larochelle（2016）引入了一种元学习方法，其中LSTM为给定情节更新分类器的权重。 Munkhdalai＆Yu（2017）还提出了一种元学习架构，可跨任务学习元级知识，并通过快速参数化改变其归纳偏见。 Finn等。 （2017）正在使用基于梯度下降的不可知模型元学习器，目标是训练一个分类模型，以便在给定新任务的情况下，少量的梯度步骤和很少的数据就足以泛化。 最近，Mishra等。 （2017）使用的时间卷积是基于扩张卷积的深度递归网络，该方法还利用了来自子集T的上下文信息，从而提供了很好的结果。
研究的另一个相关领域涉及基于图结构数据的深度学习架构。 GNN首先是在Gori等人中提出的。（2005）； Scarselli等。 （2009年），作为可训练的经常性消息传递，其固定点可以有区别地进行调整。随后的工作 李等。 （2015）； Sukhbaatar等。 （2016）通过解开递归层权重放宽了模型，并通过选通机制提出了一些非线性更新。图神经网际络实上是卷积网络对非欧几里德图的自然概括。布鲁纳等。 （2013）； Henaff等。 （2015年）提出学习图拉普拉斯算子的平滑谱倍增器，尽管计算成本很高，Defferrard等人（2015年）提出。 （2016）； Kipf＆Welling（2016）通过学习图拉普拉斯算子的多项式解决了计算瓶颈，从而避免了特征向量的计算并完成了与GNN的连接。特别是，Kipf＆Welling（2016）是第一个提出在半监督分类问题上使用GNN的人。我们请读者参考Bronstein等。 （2017）对该主题进行详尽的文献综述。 GNN和类似的神经消息传递模型正在许多不同领域中找到应用。 Battaglia等。

3.问题设置

我们首先描述一般的设置和符号，然后将其具体化到few-shot学习，半监督学习和主动学习的情况。
我们考虑从部分标记的图像集合的分布P中提取的输入/输出对(Ti , Yi)i.

任意的值s,r,t和K. s为有标签样本的数量。r无标签样本的数量（r>0用来监督学习和主动学习脚本）。t是要分类的样本数。K是类别数。我们将关注t=1的情况，每个任务T只分类一个样本。表示RN上特定类的图像分布。在我们的上下文中，目标 Yi与没有观察到标签的指定图像的图像类别x 1，…，x t∈T i相关联。给定训练集｛（Ti,Yi）i｝ i<=L,我们考虑无监督的目标函数：

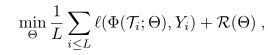
使用第4节中指定的模型Φ（T;Θ）= p（Y | T），R是标准正则化目标。

Few-shot Learning：当r = 0，t = 1且s = qK时，集合中只有一个图像带有未知标签。 此外，如果每个标签正好出现q次，则此设置称为q-shot，K-way学习。 (不太懂？？)
Semi-supervised Learning:当r> 0且t = 1时，输入集合包含辅助图像〜x 1，…，〜xr，模型可利用这些样本从共同分布中抽取出的样本作为模型，从而提高预测精度。 确定输出。

Active Learning:在主动学习设置中，学习者具有从子集合{〜x 1，…，〜x r}请求标签的能力。 我们感兴趣的是，对于s + r = s 0; s<

4 模型

本节介绍基于简单的端到端图神经网络架构的方法。 我们首先说明如何将输入上下文映射到图形表示中，然后详细说明体系结构，然后说明此模型如何概括许多以前发布的少量学习型体系结构。

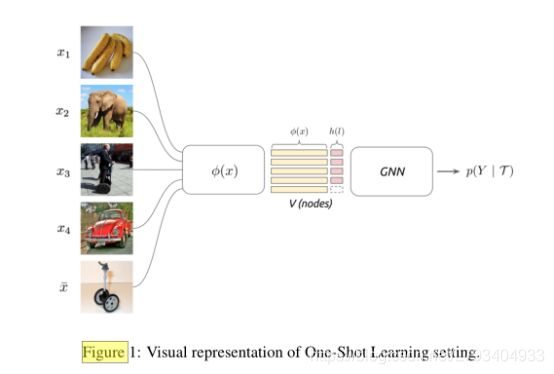
4.1 SET AND GRAPH INPUT REPRESENTATIONS

输入T包含标记和未标记图像的集合。 few-shot学习的目标是将标签信息从标记的样本传播到未标记的查询图像。 信息的传播可以形式化为对由输入图像和标签确定的图形模型的后验推断。
继最近的一些工作之后，这些工作使用消息传递和在图上定义的神经网络进行了后验推断
我们将T与完全连通的图G T =（V，E）关联，其中节点v a∈V对应于T中存在的图像（标记的和未标记的）。 在这种情况下，该设置未在图像x a和x a ‘之间指定固定的相似度e a，a ‘，这表明一种类似于吉尔默（Gilmer）等人的方法，是利用参数模型以判别方式学习这种相似度的方法。 （2017），例如暹罗神经体系结构。 这个框架与Vinyals等人的集合表示紧密相关。 （2016），但扩展了使用下面将详细介绍的图神经网络形式主义的推理机制。

4.2 GNN

GraphNeuralNetworks，在Gorietal（2005）中介绍； Scarsellietal（2009），在Li等人中进一步简化。 （2015）； Duvenaud等。 （2015）； Sukhbaatar等。 （2016年）是基于图G =（V，E）的局部算子的神经网络，在表达性和样本复杂性之间提供了强大的平衡。 参见Bronstein等。 （2017）对图上深度学习的模型和应用的最新调查。
简单地说，给定加权图G的顶点上的输入信号F∈R V×d，我们考虑图本征线性算子的A族，该族局部作用于该信号。 最简单的是邻接算子其中，且wi，j具有相关权重 。 GNN层Gc（·）接收信号x（k）∈R V×d k作为输入，并产生x（k + 1）∈R V×d k + 1作为:

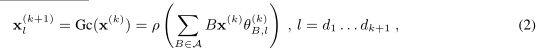
,是训练的参数并且p(.)是point-wise非线性。选择的是“Leaky”Relu.
作者已经用这种基本公式探索了几种建模变量，方法是用门操作代替逐点非线性，Duvenaud等人。 （2015），或将生成器族推广为拉普拉斯多项式Defferrardetal（2016）; Kipf＆Welling（2016）; Brunaetal。（2013），或包括A到A的2 J次幂，AJ = min（1，A 2J ）编码每个节点的2个J跳邻居Bruna＆Li（2017）。 形式为（2）的级联运算能够近似各种图推理任务。 特别是受消息传递算法启发，Kearnes等人。 （2016）； Gilmer等。 （2017）推广了GNN以便从当前节点隐藏表示中学习边缘特征〜A（k）：

ϕ是一个对称函数，参数化为 神经网络。 在这项工作中，我们考虑在两个向量节点之间的绝对差之后堆叠的多层感知器。 参见等式。 4：

那么ϕ是一个度量，可以通过对两个节点的各个特征之间的绝对差进行非线性组合来学习。 使用该架构，通过构造来满足对称距离特性ϕ〜θ（a，b）= ϕ〜θ（b，a），并且容易学习自身距离特性ϕ〜θ（a，a）= 0。
然后通过使用每一行上的softmax将可训练的邻接关系归一化。 通过将边缘特征内核〜A（k）添加到生成器族A = {〜A（k），1}中并应用（2），可以获得针对节点特征的结果更新规则。 邻接学习在输入集被认为具有某种几何结构，但度量不是先验的情况下（例如我们的情况）尤其重要。
在一般图形中，网络深度选择为图形直径的数量级，以便所有节点都可以从整个图形中获取信息。 但是，在我们的上下文中，由于图形紧密连接，因此深度被简单地解释为赋予模型更多的表达能力。

构造节点初始特征：输入集合T如下映射到节点特征中。 对于具有已知标签li的图像x i∈T，标签的one-hot编码与图像嵌入的特征在GNN输入处连接在一起。

其中φ是CNN网络，是标签的one-hot编码。 φ的体系结构详细信息在6.1.1和6.1.2节中进行了详细说明。 对于具有未知标签li的图像〜xj，¯xj 0，我们通过用K-simplex上的均匀分布替换h（l）来修改先前的构造，以解决关于标签变量的完全不确定性：(???)，类似地对于x。
4.3 与现有模型的关系
Few-shot学习的图神经网络公式概括了文献中提出的许多最新模型。
Siamese Networks暹罗网络 暹罗网络Koch等。 （2015）可以解释为模型的单层消息传递迭代，并使用相同的初始节点嵌入x(0) = ，使用不可训练的边缘特征.

和结果标签估计：

用u从x中选择标签字段(u是有标签的)。 在该模型中，学习被简化为学习欧氏度量与标签相似度一致的图像嵌入φ（x i）。

Prototypical Networks （原型网络）：原型网络Snell等。 （2017）通过将信息聚合在一起来发展暹罗网络，其中每个集群由具有相同标签的节点确定。 此操作也可以通过gnn如下完成。 我们认为：

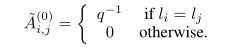
其中q是每个类样本的数量 ，并且

其中x(0)定义在 Siamese Networks。最后，我们将先前的核〜A（1）= softmax（ϕ）应用于x（1）以产生类原型：

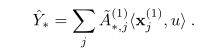
Matching Networks(匹配网络)：匹配网络Vinyals等。 （2016）使用集合表示来表示T中的图像，类似于我们提出的图神经网络模型，但有两个重要区别。首先，在这种集合表示中考虑的注意力机制类似于边缘特征学习，区别在于机制始终与相同的节点嵌入相关，而不是我们的堆叠邻接学习，后者更接近于Vaswani等人。 （2017）。换句话说，代替（3）中的注意核，匹配网络考虑了以下形式的注意机制：A（k），j = ϕ（x（k），x（T）j），其中x（T j是使用双向LSTM获得的支持集元素的编码函数。在那种情况下，因此独立于目标图像来计算支持集编码。其次，在整个模型中分别处理标签和图像字段，最后一步是使用经过训练的内核线性汇总标签。这可能会阻止模型在中间阶段利用标签和图像之间的复杂依赖性。

5 训练

接下来，我们将介绍如何在我们考虑的不同设置中训练GNN的参数：few-shot学习，半监督学习和主动学习。

5.1few-shot和半监督学习

在这种设置中，仅要求模型预测与图像相对应的标签Y，以对与图中的节点∗相关的x∈T进行分类。 因此，GNN的最后一层是softmax mappin

半监督设置的训练是相同的-唯一的区别是，节点的初始标签字段将由对应于〜x j的节点上的均匀分布填充。

5.2主动学习
略

6 实验

对于few-shot，半监督和主动学习实验，我们使用了Lake等人提供的Omniglot数据集。 （2015年）和Vinyals等人引入的Mini Imagenet数据集。 （2016）是ILSVRC-12 Krizhevsky等人的小版本。 （2012）。 所有实验均基于q-shot，K-way设置。 对于所有实验，我们在训练和测试中都使用相同的q-shot和K-way值。

6.1 数据集和实现

6.1.1 OMNIGLOT

Dataset:Omniglot是一个来自50个不同字母的1623个字符的数据集，每个字符/类都由20个不同的人绘制而成。 跟随Vinyals等。 （2016）实施，我们将数据集分为1200个类别进行训练，其余423个类别进行测试。 正如Santoro等人所提出的，我们将数据集增加了90度的倍数。 （2016）。
Architectures：受到Vinyals等人的嵌入架构的启发。 （2016），紧随Mishra等人。 （2017年），使用CNN作为嵌入φ函数，该函数由四个堆叠的{3×3卷积层和64个滤镜，批量归一化，2×2最大池化，leakage-relu}堆叠块组成，输出通过 完全连接的层，最终64维嵌入。 对于GNN，我们使用了3个块，每个块由1）计算邻接矩阵的模块和2）图卷积层组成。 每个模块的更详细描述可以在图3中找到。

6.1.2 MINI -IMAGENET

数据集：Mini-Imagenet是Vinyals等人提出的单次学习更具挑战性的数据集。 （2016）源自原始ILSVRC-12数据集Krizhevsky等。 （2012）。 它由100个不同类别的84×84 RGB图像组成，每个类别600个样本。 创建它的目的是增加一次性任务的复杂性，同时保持轻量级数据集的简单性，使其适合于快速原型制作。 我们使用Ravi＆Larochelle（2016）提出的拆分方法进行训练，分为64个班级，有16个班级用于验证，有20个班级用于测试。 使用64个类别进行训练，而使用16个验证类别仅用于提前停止和参数调整。
体系结构：用于Mini-Imagenet的嵌入体系结构由4个卷积层，然后是完全连接的层，从而形成128维的嵌入。 这个灯体系结构可用于快速原型制作：

这两个drop out有助于避免Mini Imagenet数据集中的GNN过度拟合。 GNN架构与Omniglot相似，它由3个块组成，每个块在图1中进行描述。

6.2 few shot

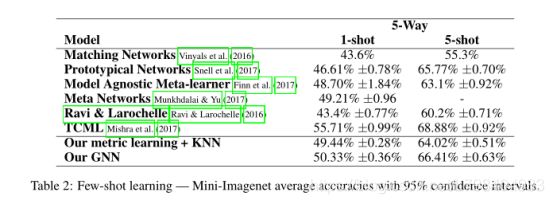
表1和表2分别展示了Omniglot和Mini-Imagenet的few-shot学习实验。
我们通过对两个数据集执行不同的q-shot，K-way实验来评估模型。对于每个few-shot任务T，我们从数据集中采样K个随机类，并从每个类采样q个随机样本。从该K个类别中选择一个额外的样本进行分类。 Omniglot：GNN方法在提供竞争性结果的同时仍比其他方法更简单。在5路和20路one-shot实验中达到了最先进的结果。在20路one-shot设置中，GNN的效果比Munkhdalai＆Yu（2017）略好，但仍然是一种更简单的方法。来自Mishra等人的TCML方法。 （2017）在4个实验中有3个处于相同的置信区间内，但对于20向5次射击，它的效果略好一些，尽管参数的数量从〜5M（TCML）减少至〜300K（3层GNN ）。
在Mini-Imagenet表中，我们还提供了一个基线“我们的度量学习+ KNN”，其中节点之间没有任何信息汇总，这是在成对可学习度量ϕθ（x（0 ）i，x（0）j）并经过端到端训练，与其他现有技术相比，该可学习的指标本身具有竞争优势。即使这样，还是有很大的改进（从
通过使用完整的GNN架构汇总节点之间的信息时，对于5张5幅微型Waynet网络设置，可以看到64.02％到66.41％）。在Mini-Imagenet实验的不同论文中使用了多种嵌入函数φ，在本例中，我们使用的是4转换的简单网络。层，然后是\完全连接的层（第6.1.2节），它使我们能够在GNN和度量学习+ KNN之间进行比较，这对于快速原型设计很有用。 Mishra等人已证明，更复杂的嵌入可以产生更好的结果。 （2017年）使用深度残差网络作为嵌入网络，大大提高了准确性。关于小米的TCML架构:

6.3监督学习

6.4 主动学习

7.总结