归并排序中的逆序对问题和前后缀和的用法
前言
我们在数据结构中接触过归并排序,其核心是分治思想,我们把原来的无序的数组分成两部分,对于每部分,再继续分解成更小的两部分......在归并排序中,我们只是简单的把数组分成两半即可,到分解到不能分解之后再对其进行排序,接着,我们把每次分开的部分合并到一起,合并也是归并排序的核心操作,其过程类似于交换排序,时间复杂度为O(nlogn),空间复杂度为O(n),需要开辟临时的数组存储交换结果。
我们可以发现,在归并排序的过程中,我们注意到存在判断过程,存在后面的元素比前面的元素小的情况,这种情况我们称其为逆序对,在求解逆序对问题时,我们可以利用这个过程,来达到计数的目的。
这种逆序对往往可以和前后缀和结合起来求解一个集合满足条件的子串问题(注意是子串,不是子集,子串是连续的子集,而子集可以是不连续的数组中的元素),下面我们还是通过题目来感受下这些用法。
1.简单的逆序对问题
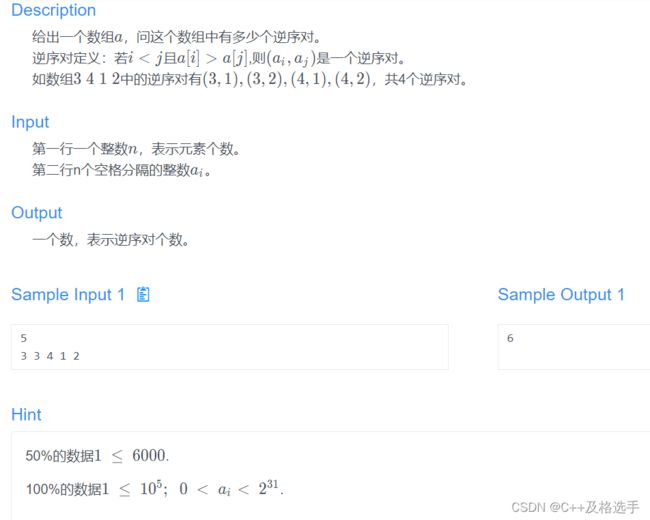
逆序对个数
读完题目,你第一个想到的是不是用两层循环暴力搜索呢?哎,浅了浅了,作为算法题出现能那么容易让你过吗?暴力搜的话,时间复杂度为O(n^2) ,如果在有十万个数据的话,一定会让你超时的,所以我们要换种方法。
逆序对问题的一种标准解法就是归并排序法,不过,归并排序有一个固定的缺点,它需要多次复制数组,所以就导致了归并排序的空间复杂度要高一些。
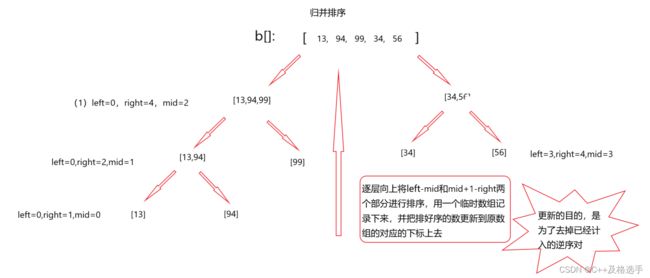
我们观察一下这个归并的过程:
(1)在子序列内部,元素都是有序的,不存在逆序对;逆序对只存在于不同的子序列之间。
(2)合并两个子序列时,如果前一个子序列的元素比后面子序列的元素小,那么不会产生逆序对;如果前一个子序列的元素比后面子序列的元素大,就会产生逆序对,不过,在一次合并中,产生的逆序对不止一个,像上面的例子,我们把34放入b中的时候,产生了(94,34)和(99,34)两个逆序对,具体的规律就是对于两个有序数组,在某次比较中,如果后面的数组的元素较大,那么前面的数组从当前位置开始,一直到结束位置的下标,每一个元素都会与之组成一个逆序对,也即mid-i+1个逆序对。
需要注意的是,我们利用辅助数组来更新已经计入逆序对的数据,将一次判断中为逆序对的数据交换并存入b中(注意此时应和当前的原数组下标保持一致,不可从0或者1开始,因为后序我们还要把交换后的数据更新到原数组中去以防止已经计数过得逆序对再次被计数)
#include
#define maxn 100005
using namespace std;
int n;
int a[maxn];
int temp[maxn];
long long ans = 0;
void f(int a[], int left, int right)
{
if (left >= right)
return ;
int mid = (left + right) >> 1;
f(a, left, mid);
f(a, mid + 1, right);
//printf("%d %d\n", left, right);
int i, j, k;
for (i = left, j = left, k = mid + 1; i <= right && j <= mid && k <= right;i++)
{
if (a[j] <= a[k])
temp[i] = a[j++];
else
{
temp[i] = a[k++];
ans += (mid - j + 1);
}
}
while (j <= mid) temp[i++] = a[j++];
while (k <= right) temp[i++] = a[k++];
for (i = left; i <=right; i++)//更新到对应的下标的位置
a[i] = temp[i];
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
f(a, 0, n - 1);
printf("%lld", ans);
return 0;
} 2.前后缀和的应用
首先,什么是前后缀和?
一个长度为n的数组,它的前缀和定义为sum[i]=a[0]~a[i]的和,如sum[0]=a[0],sum[1]=a[0]+a[1]......
利用递推,可以在O(n)时间内求得所有的前缀和:sum[i]=sum[i-1]+a[i];
如果想要计算出指定区间内的和,则有,a[i]+......+a[j]=sum[j] - sum[i-1];
而我们的后缀和也具有相类似的定义,只是后缀和是从后面开始加而已。
问题引入
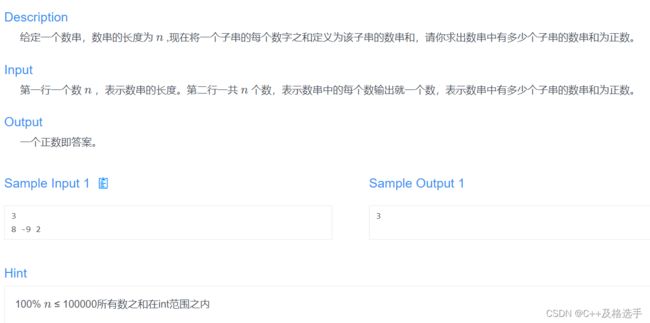
后缀和问题
数串问题
为什么不采用前缀和?
前缀和来求子串的和大于0的话,其实必经之路还是两层循环,最后还是要从头到尾的遍历一遍数据,时间复杂度还是很高,而且它每次只能求出一个子串,因此我们必须要引入更加高效的算法,一次能算出多个子串和大于0的子串。
为什么采用后缀和?
之所以采用后缀和,是因为我们在写出后缀和的结果时,发现其可以和归并排序判断逆序对产生联系,对于后缀和数组来说,如果数组前半部分中的元素比后半部分的元素大(存在逆序对),那么从前半部分的该元素向后一直到前半部分结束,其元素一定都会比后半部分的元素大,也就是在区间[左半部分下标,右半部分下标)的子串大于0,也就是bsum[i]-bsum[j]>0,i
#include
#define maxn 100005
using namespace std;
int n;
int a[maxn];
int temp[maxn];
int bsum[maxn];
long long ans = 0;
void f(int a[], int left, int right)
{
if (left >= right)
return;
int mid = (left + right) >> 1;
f(a, left, mid);
f(a, mid + 1, right);
//printf("%d %d\n", left, right);
int i, j, k;
for (k = left, i = left, j = mid + 1; k <= right && i <= mid && j <= right; k++)
{
if (bsum[i] <= bsum[j])
{
temp[k] = bsum[i++];
}
else
{
temp[k]=bsum[j++];
ans += mid - i + 1;
}
}
while (i <= mid)temp[k++] = bsum[i++];
while (j <= right)temp[k++] = bsum[j++];
for (i = left; i <= right; i++)
bsum[i] = temp[i];
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
}
for (int i = n; i>=1; i--)
bsum[i] = bsum[i+1] + a[i];//后缀和数组
/*for (int i = 1; i <= n; i++)
printf("%d ", bsum[i]);*/
//我们这里令bsum[n+1]=0,所以我们要将传bsum的n个数进去,因为我们也需要算出bsum[i]-bsum[n+1]也即i-最后一个数据的下标的值,如果不传入n+1的话,就无法计算到最后一个数据的子串和
f(bsum, 1, n+1);
printf("%lld", ans);
return 0;
}
当然,你也可以直接将a数组变为后缀和数组传入,可以节省后缀和数组的开辟空间;
对于为什么后缀和数组要传入第n+1个数,是因为我们需要用到bsum[n+1]来计算bsum[i]-bsum[n+1]的数据来计算i-n的子串和;