目录
- 例1:分糖果(easy)(排序、贪心)
- 例2:摇摆序列(medium)(贪心)
- 例3:移除K个数字(medium)(栈、贪心)
- 例4-a:跳跃游戏(medium)(贪心)
- 例4-b:跳跃游戏2(hard)(贪心)
- 例5:射击气球(medium)(排序、贪心)
- 例6:最优加油方法(hard)(堆、贪心)
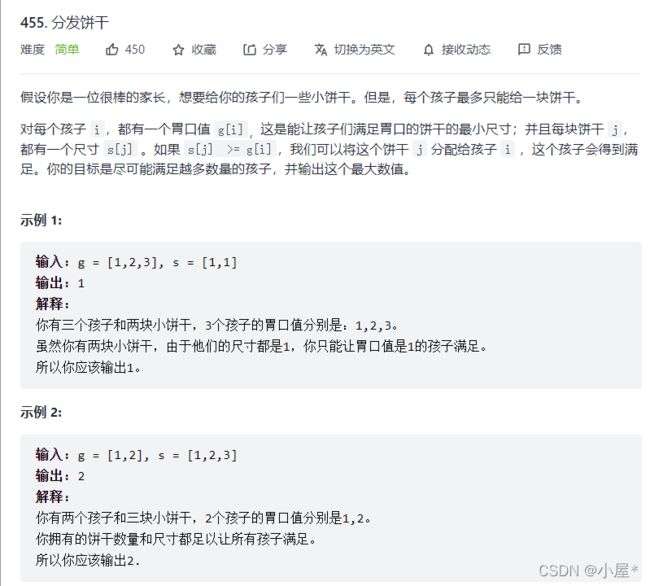
例1:分糖果(easy)(排序、贪心)

class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
std::sort(g.begin(),g.end());
std::sort(s.begin(),s.end());
int child=0;
int cookie=0;
while(child<g.size() && cookie<s.size()){
if(g[child]<=s[cookie]){
child++;
}
cookie++;
}
return child;
}
};
例2:摇摆序列(medium)(贪心)


class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if(nums.size()<2){
return nums.size();
}
static const int BEGIN=0;
static const int UP=1;
static const int DOWN=2;
int STATE=BEGIN;
int max_length=1;
for (int i=1;i<nums.size();i++){
switch(STATE){
case BEGIN:
if (nums[i]>nums[i-1]){
STATE=UP;
max_length++;
}
else if(nums[i-1]>nums[i]){
STATE=DOWN;
max_length++;
}
break;
case UP:
if(nums[i]<nums[i-1]){
STATE=DOWN;
max_length++;
}
break;
case DOWN:
if(nums[i]>nums[i-1]){
STATE=UP;
max_length++;
}
break;
}
}
return max_length;
}
};
例3:移除K个数字(medium)(栈、贪心)


class Solution {
public:
string removeKdigits(string num, int k) {
std::vector<int>S;
std::string result="";
for (int i=0;i<num.size();i++){
int number=num[i]-'0';
while(S.size() !=0 && k>0 &&S[S.size()-1]>number){
S.pop_back();
k--;
}
if (number !=0 || S.size()!=0){
S.push_back(number);
}
}
while(S.size()!=0 && k>0){
S.pop_back();
k--;
}
for (int i=0;i<S.size();i++){
result.append(1,'0'+S[i]);
}
if(result==""){
result='0';
}
return result;
}
};
例4-a:跳跃游戏(medium)(贪心)



class Solution {
public:
bool canJump(vector<int>& nums) {
std::vector<int> index;
for (int i = 0; i < nums.size(); i++) {
index.push_back(i + nums[i]);
}
int jump = 0;
int max_index = index[0];
while (jump < nums.size() && jump <= max_index) {
if (max_index < index[jump]) {
max_index = index[jump];
}
jump++;
}
if (jump == nums.size()) {
return true;
}
return false;
}
};
class Solution {
public:
bool canJump(vector<int>& nums) {
int step = 1;
for (int i = nums.size() - 2; i >= 0; i--)
{
if (nums[i] >= step)
{
step = 1;
continue;
}
else
{
step++;
}
}
if (step == 1) return true;
else return false;
}
};
class Solution :
def canJump(self, nums) :
max_i = 0
for i, jump in enumerate(nums) :
if max_i >= i and i + jump > max_i:
max_i = i + jump
return max_i >= i
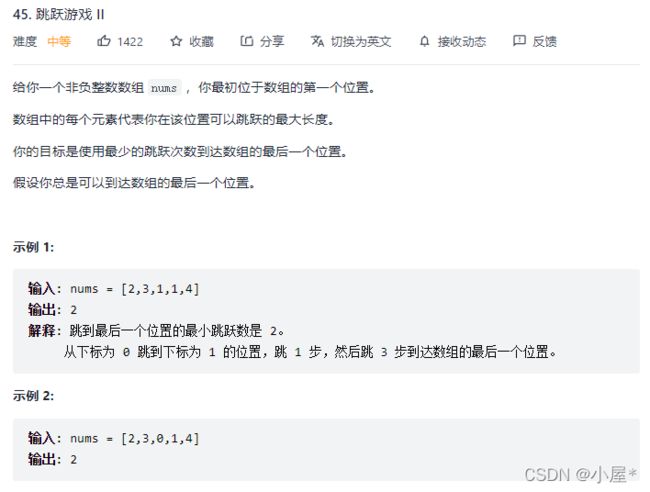
例4-b:跳跃游戏2(hard)(贪心)
class Solution {
public:
int jump(vector<int>& nums) {
if (nums.size() < 2) {
return 0;
}
int current_max_index = nums[0];
int pre_max_index = nums[0];
int jump_min = 1;
for (int i = 1; i < nums.size(); i++) {
if (i > current_max_index) {
jump_min++;
current_max_index = pre_max_index;
}
if (pre_max_index < i + nums[i]) {
pre_max_index = i + nums[i];
}
}
return jump_min;
}
};
例5:射击气球(medium)(排序、贪心)


bool cmp(const vector<int>& a, const vector<int>& b) {
return a[0] < b[0];
}
class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
if (points.size() == 0) {
return 0;
}
std::sort(points.begin(), points.end(), cmp);
int shoot_num = 1;
int shoot_begin = points[0][0];
int shoot_end = points[0][1];
for (int i = 1; i < points.size(); i++) {
if (points[i][0] <= shoot_end) {
shoot_begin = points[i][0];
if (shoot_end > points[i][1]) {
shoot_end = points[i][1];
}
}
else {
shoot_num++;
shoot_begin = points[i][0];
shoot_end = points[i][1];
}
}
return shoot_num;
}
class Solution(object):
def findMinArrowShots(self, points):
"""
:type points: List[List[int]]
:rtype: int
"""
if not points:
return 0
points.sort()
shoot_num=1
shoot_begin=points[0][0]
shoot_end = points[0][1]
for i in range(1,len(points)):
if points[i][0]<=shoot_end:
shoot_begin=points[i][1];
if shoot_end>points[i][1]:
shoot_end=points[i][1]
else:
shoot_num+=1
shoot_begin=points[i][0]
shoot_end=points[i][1]
return shoot_num
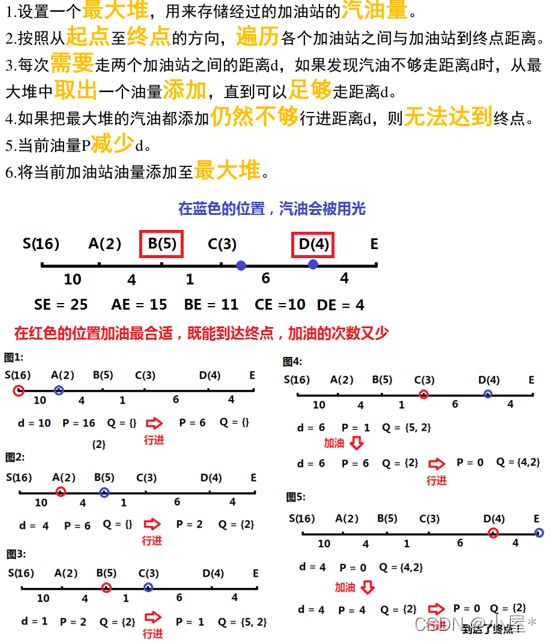
例6:最优加油方法(hard)(堆、贪心)

bool cmp(const std::pair<int,int>& a, const std::pair<int,int>& b) {
return a.first < b.first;
}
int get_min_stop(int L, int P, std::vector<std::pair<int, int>>& stop) {
std::priority_queue<int> Q;
int result = 0;
stop.push_back(std::make_pair(0, 0));
std::sort(stop.begin(), stop.end(), cmp);
for (int i = 0; i < stop.size(); i++) {
int dis = L - stop[i].first;
while (!Q.empty() && P < dis) {
P += Q.top();
Q.pop();
result++;
}
if (Q.empty() && P < dis) {
return -1;
}
P = P - dis;
L = stop[i].first;
Q.push(stop[i].second);
}
return result;
}













