数据结构与算法--图的表示与常用算法
什么是图?
图(Graph)形结构中,是一种非线性结构,在图中每一个元素都可以有0或多个前驱,也可以有多个后驱。节点之间的关系是任意的,即图中任意两个数据元素之间都有可能相关。
图的术语
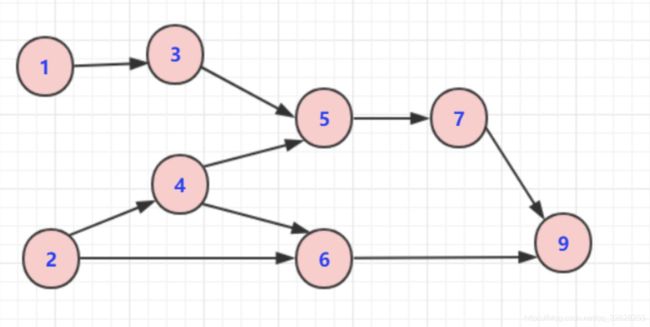
- 顶点:带有数字的圈圈都叫做顶点
- 边:连接两个顶点之间的线叫做边
- 度数:分为入度和出度,入度表示被指向的数,出度表示出发的数
- 路径:如1到5的路径
- 有向图、无向图:边是否带有箭头,图中表示有向图
为什么需要图?
假设一个项目中有多个任务,这些任务之间部分是存在现后顺序的,那么如何去正确的描述这种关系呢?
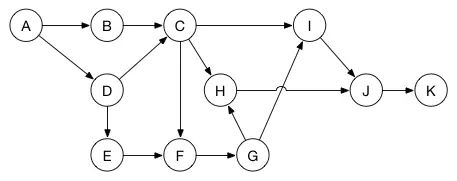
如图所示,通过图的方式,可以很方便的表示任务的现后顺序,每一个顶点表示一个任务。在B和D任务都完成之前,任务C不可以开始;在任务A开始之前,任务B和D都不能开始。
通过图的方式可以把问题描述清楚,就可以通过不同的图算法来进行求解,比如使用深度优先搜索算法来执行拓扑排序,保证等待任务完成时间的最小化。
图的表示
邻接矩阵表示法
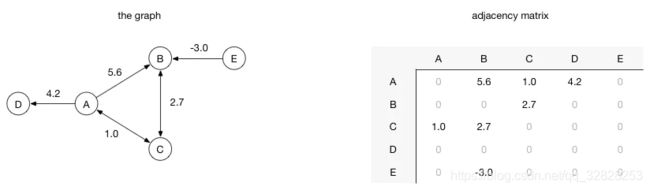
在邻接矩阵中,使用行和列来表示顶点,每个单元格中表示的是两个顶点之间的权重。例如顶点A到顶点B有一条权重为5.6的边,在矩阵中A行B列位置的元素值就应该是5.6
优点:
- 便于判断两个顶点是否有边,只需看元素是否有值即可
- 适用于密集图,空间复杂度为:
O(顶点个数+边的个数)
缺点:
- 不便于插入和删除节点,在图中插入顶点后矩阵需要重新按照新的行/列创建,然后将老的矩阵已有数据复制到新的矩阵中
- 不便于统计与某个顶点相连的边的数目,每次都需要遍历整个表
- 不适用于稀疏图,效率不如邻接表
邻接表表示法
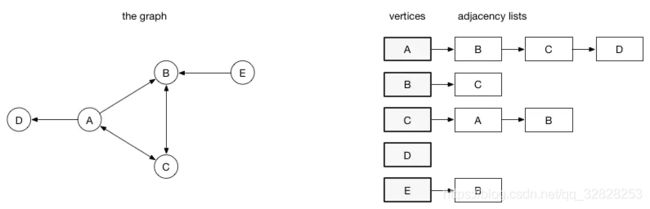
在邻接表实现中,每一个顶点会存储一个从它这里出发的列表。
比如顶点A出发可以到B、C、D,那么A的列表中会有3条边。
优点:
- 便于插入和删除节点,只需要修改一下单链表即可
- 便于统计与这个顶点相连的边的数目,只需要看单链表的大小即可
- 空间效率高,空间复杂度为
O(顶点个数+边的个数),更适用于表示稀疏图
缺点:
- 不利于判断两个顶点之间是否有边,需要花费
O(顶点个数)的时间复杂度扫描邻接表 - 不利于统计有向图顶点的入度,对于无向图来说,顶点对应的链表长度就是该顶点的度,但是在有向图中,链表的大小只能表示出度,而求入度较困难。
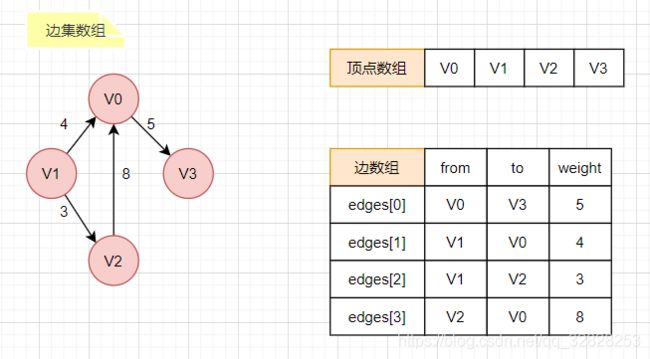
边集数组
边集数组是由两个一维数组构成。
- 一个数组存储顶点的信息
- 一个数组存储边的信息,每个元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。
优点:
- 更适合对边依次进行处理的操作场景,而不适合对顶点相关的操作
缺点:
- 在边集数组中要查找一个顶点的度需要扫描整个边数组,效率不高
- 插入删除节点需要遍历整个边数组进行删除,效率不高
几种表示方法比较(V代表顶点,E代表边):
| 操作 | 邻接列表 | 邻接矩阵 | 边集数组 |
|---|---|---|---|
| 存储空间 | O(V + E) | O(V^2) | |
| 添加顶点 | O(1) | O(V^2) | |
| 添加边 | O(1) | O(1) | |
| 检查相邻性 | O(V) | O(1) |
图有哪些算法?
广度优先搜索算法 BFS(breadth-first search)
优先广度遍历,一层遍历完成后再遍历下一层
优点
- 对于解决最短或最少问题特别有效,而且寻找深度小
- 每个结点只访问一遍,结点总是以最短路径被访问,所以第二次路径确定不会比第一次短
缺点
- 内存耗费量大(需要开大量的数组单元用来存储状态)
代码中使用队列+Set实现:
/**
* 广度优先搜索算法 BFS(breadth-first search)
*
* @param node 访问出发点
*/
private void bfs(Node node) {
Queue<Node> queue = new LinkedList<>();
Set<Node> visitedNode = new HashSet<>();
// 访问首节点
queue.add(node);
visitedNode.add(node);
// 广度优先遍历
while (!queue.isEmpty()) {
Node curNode = queue.poll();
System.out.println(node.getValue());
// 获取下一层的所有结点
List<Node> nextNodes = curNode.getNextNodes();
for (Node nextNode : nextNodes) {
// 未被访问过则加入队列
if (!visitedNode.contains(nextNode)) {
queue.add(nextNode);
visitedNode.add(nextNode);
}
}
}
}
基本过程如下:
- 访问出发点Vi
- 访问Vi所有未被访问过的邻接点Vi1、Vi2、Vi3…,并将它们标记为已访问过(添加到visitedNode集合)
- 然后再按照Vi1、Vi2、Vi3…的次序访问每一个顶点并获取此顶点未访问过的邻接点Vi11、Vi12、Vi13…,以此类推,直到遍历到最后一层
深度优先搜索算法 DFS(depth-first search)
深度优先遍历,走到最深的一层,先把深的遍历完成再一步步往上一层走进行遍历
优点
- 能找出所有解决方案
- 优先搜索一棵子树,然后是另一棵,所以和广搜对比,有着内存需要相对较少的优点
缺点
- 要多次遍历,搜索所有可能路径,标识做了之后还要取消。
- 在深度很大的情况下效率不高
代码中使用栈+Set实现:
/**
* 深度优先搜索算法 DFS(depth-first search)
*
* @param node 访问出发点
*/
private void dfs(Node node) {
Stack<Node> stack = new Stack<>();
Set<Node> visitedNode = new HashSet<>();
// 访问首顶点
stack.push(node);
visitedNode.add(node);
// 深度优先遍历
while (!stack.empty()) {
Node cur = stack.pop();
for (Node nextNode : cur.getNextNodes()) {
if (!visitedNode.contains(nextNode)) {
// 有相邻顶点,则将当前顶点压入栈
stack.push(cur);
// 相邻顶点压入栈
stack.push(nextNode);
// 标记已被访问过
visitedNode.add(nextNode);
System.out.println(nextNode.getValue());
break;
}
}
}
}
基本过程如下:
- 将访问的出发顶点Vi压入栈并标记以访问
- 遍历栈,并pop出顶点Vi,查找此Vi相邻的所有顶点,遍历所有相邻顶点
- 将当前顶点Vi压入栈
- 将当前顶点的相邻顶点Vi1压入栈
- 标记Vi1已被访问过
- 继续遍历栈,pop出顶点Vi1,继续按照以上步骤2循环,直至所有顶点都被访问过
拓扑排序算法(Topological Sorting)
拓扑排序是一个有向无环图(DAG,Directed Acyclic Graph)的所有顶点的线性序列
约束条件:每个顶点出现且只出现一次
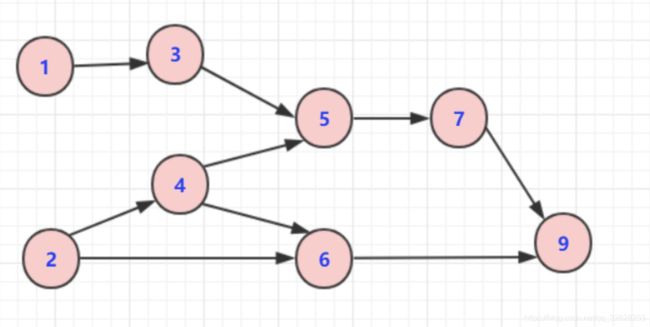
将入度为0的顶点进行遍历,将相邻结点的入度减1,并断开当前顶点,然后继续查找,找到下一个入度为0的顶点,以下一个入度为0顶点带入重复如上步骤
通过队列+Map实现:
/**
* 拓扑排序(Topological Sorting)
*
* @param graph 有向无环图(DAG,Directed Acyclic Graph)
* @return 排序后的集合
*/
private static List<Node> topologySort(Graph graph) {
Queue<Node> zeroInQueue = new LinkedList<>();
Map<Node, Integer> inMap = new HashMap<>();
// 遍历图的所有顶点,其实就是初始化集合
for (Node node : graph.getNodeMap().values()) {
// 找出入度为0的顶点并加入zeroInQueue队列
if (node.getIn() == 0) {
zeroInQueue.add(node);
}
// 加入入度数map,key为结点,value为入度数
inMap.put(node, node.getIn());
}
// 保存排序结果的集合
List<Node> result = new ArrayList<>();
// 遍历入度为0的栈
while (!zeroInQueue.isEmpty()) {
Node cur = zeroInQueue.poll();
result.add(cur);
// 获取相邻顶点并再次遍历并加入对应集合
for (Node nextNode : cur.getNextNodes()) {
// 入度减1并加入集合
inMap.put(nextNode, inMap.get(nextNode) - 1);
// 入度为0的
if (inMap.get(nextNode) == 0) {
zeroInQueue.add(nextNode);
}
}
}
return result;
}
基本过程如下:
- 根据graph参数获取所有顶点并加入对应集合和栈
- pop入度为0的结点Vi
- 将顶点Vi加入结果集合result
- 查找Vi所有相邻顶点Vix
- 将相关联的顶点Vix入度减1,如果相关联的顶点入度为0则加入zeroInQueue队列
- 继续判断栈是否为空,不为空继续重复步骤2,直到zeroInQueue队列为空,也就是没有入度为0的顶点了
- 返回最终排序后的结果集合
最小生成树算法 MST(minimum spanning tree)–Prim(普里姆)算法
图的生成树是它的一棵含有其所有顶点的无环连通子图。
其中一幅"加权图的最小生成树"是它的一颗总权值和最小(树中所有边的权值之和)的生成树
基本过程:从某个顶点出发找到该点所有的边,再从中找到最小的边,然后最小边的对应顶点再重复如上步骤循环,直到找到所有顶点
通过优先优先队列+Set实现:
/**
* 最小生成树 MST(minimum spanning tree)
* 采用的是贪心算法
*
* @param graph 有向无环图(DAG,Directed Acyclic Graph)
* @return 最小生成树
*/
private Set<Edge> prim(Graph graph) {
// 排序后的集合
Set<Edge> result = new HashSet<>();
// 优先队列
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
// 顶点集合
Set<Node> nodeSet = new HashSet<>();
// 遍历图中的所有顶点
for (Node node : graph.getNodeMap().values()) {
if (!nodeSet.contains(node)) {
// 获取此顶点的所有边并加入优先队列
List<Edge> edges = graph.getEdges(node);
edges.forEach(e -> priorityQueue.add(e));
// 遍历优先队列,权重最小的总是在栈顶
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();
Node to = edge.getTo();
// 没有被访问过的顶点
if (!nodeSet.contains(to)) {
// 再去找所有边并加入优先队列
List<Edge> edgeList = graph.getEdges(to);
edgeList.forEach(e -> priorityQueue.add(e));
nodeSet.add(to);
// 加入结果集合
result.add(edge);
}
}
}
}
return result;
}
private static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.getWeight() - o2.getWeight();
}
}
基本过程如下:
- 遍历图中所有的顶点
- 如果顶点Vi没有被访问过则获取Vi的所有边并加入优先队列
- pop优先队列元素(栈顶的是权重最小的边),获取此边对应的顶点Vi1且Vi1没有被访问过
- 获取Vi1所有的边并加入优先队列、标记已被访问、加入结果集合操作
- 当下一次遍历栈时,pop出来的又是权重最小的,再重复2~3步骤…
- 最终都是按照权重最小的边且未被访问过的顶点的路径去走,走出来的路径就是最小生成树
总结
图的表示法:邻接表示法、矩阵表示法、边集数组表示法,这也是最通用的几种表示方法
图的几种算法:深度或广度优先遍历、拓扑排序、最小生成树,不同的算法作用也不同,例如深度优先遍历更加适合找出所有可能的解决方案;广度优先遍历更加适合查找顶点最短路径;