数据结构与算法-C++实现
前沿
1.数据结构和算法的理解
答:
我们如何把现实中大量而复杂的问题,以特定的数据类型和特定的存储结构保存到主存储器(内存)中。
(注:数据结构解决了数据存储的问题,比如要存储一个班级50人的成绩,可以使用数组直接在内存开辟出整块空间用于存储;但是当要存储一个学校5000人的成绩时,由于内存没有这么大整块空间用于存储,此时不能用数组,转而可以用链表方式。诸如此类的数据存储问题,都属于数据结构问题。)
以及在此基础上(数据被存储到内存后),为实现某个功能(比如查找某个元素,删除某个元素,对元素进行排序等)而执行的相应操作,这个相应的操作也叫算法。
数据结构 = 个体的存储 + 个体与个体的关系存储
(如数组,个体间的关系是连续存储;链表,上一个个体指向下一个个体的存储地址)
算法 = 对存储数据的操作
(相同的数据,采用存储数据方式不一样,对应的某个功能算法就不一样)
2.数据结构的地位
答:
数据结构是软件中最核心的课程
程序 = 算法 + 数据结构 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言
3.数据结构的主要内容
答:
一、基础知识
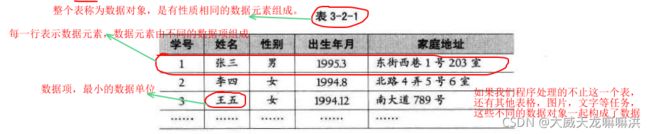
1.数据、数据对象、数据元素、数据项 的概念和关系?
2.数据结构的定义?研究数据结构的意义?逻辑结构和物理结构的概念?两者区别?
答:
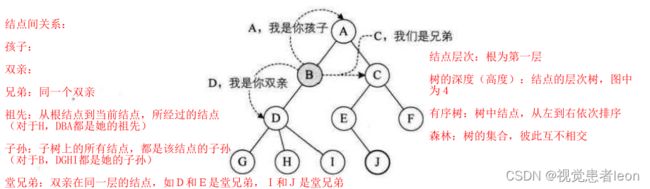
数据结构,就是数据之间的关系。计算机中,不同数据元素,彼此之间不是孤立的,而是存在某种特定关系,这种关系叫结构。
当我们编写的程序,能更好地处理具有某种特定关系的数据对象,那么这就是一个“好程序”,也是研究数据结构的意义。
逻辑结构:指数据对象中数据元素之间的关系,是逻辑意义上的关系。细分为集合结构、线性结构、树形结构、图形结构
物理结构:指数据的逻辑结构关系,在计算机上的存储形式。细分为顺序存储结构、链式存储结构。
区别:逻辑结构是面向问题的,而物理结构就是面向计算机的,其基本的目标就是将数据及其逻辑关系存储到计算机的内存中。.
3.数据类型和抽象数据类型的概念?
答:
数据类型:描述对数据的取值范围、数据的结构、以及对数据合法的操作。
可见数据类型包括了对数据结构的描述,不过由于数据结构是属于底层的知识,因此数据类型更强调对数据合法的操作。
举例:在使用整数这一数据类型时,我们不需要了解这种数据类型在计算机内存中是怎样存储的,怎样表示的,也不需要知道它在内存中执行加减乘除的运算细
节,而只需要知道这种数据类型具有逻辑上的加减乘除运算即可,所以有了数据类型,我们把注意力集中在这种数据类型所具有逻辑上的抽象特征。因此,引入数
据类型,实现了数据物理存储细节的屏蔽。这也是我们后来引入抽象数据类型的原因。
抽象数据类型:在数据结构这门课中,我们需要接触到各种不同的数据结构,我们不需要为了实现一个简单的操作,就每次关注他的底层细节。因此,我们通过定义该数据结构的抽象数据类型,屏蔽它的底层实现细节,关注对它的合法操作。因此抽象数据类型包括了数据的结构,也包括了基于这种数据结构存在的合法操作。
从我们编写的程序或者算法来说,底层算法就是抽象数据类型,它当相当于一个接口,对下封装了底层实现细节,对上提供各种操作。
(如线性表的顺序存储结构,我们通过定义一个类,类中的包括查找,插入删除等操作,就是这种数据结构的底层实现细节)
顶层算法中,在调用这种数据结构时,就只需要关注他的合法操作即可。
(我们程序在使用线性表顺序存储结构下的查找功能时,只需要调用类中查找函数即可,不需要再关心底层操作)
总结:
数据结构强调数据之间的关系,属于底层细节。
数据类型强调对数据的合法操作,也包括对数据结构的描述。
抽象数据类型,屏蔽各种数据的结构底层细节,强调对其合法的操作。其实就是C++中讲的结构体,类。
简单数据结构:整数的结构,字符的结构,数组的结构。
复杂数据结构:线性表,栈和队列,树,图
简单数据类型:整型,字符型,数组
复杂数据类型(抽象数据类型):结构体,类
可见,数据结构和数据类型从两个方面描述了数据,一个是底层,强调物理和逻辑的细节;一个是高层,强调功能操作。数据类型是对数据结构进行了接口化包装
4.算法的基本概念?定义、特性、设计要求、度量方法?
答:
算法定义:对具有某种数据结构的数据,进行功能操作(比如查找某个元素,删除某个元素,对元素进行排序等),这个操作就叫算法。
然对于不同数据结构的数据,进行相同功能的操作,算法是不同的。
算法特性:有输入,有输出,步骤的有穷性,步骤的确定性,步骤的可行性。
算法设计要求:算法正确性,算法可读性,算法健壮性,时间效率高,存储容量低。
算法的度量方法:即算法执行的时间,就是输入规模n与算法需要的基本操作数量f(n)之间的关系。如f(n)=1,f(n)=n…
5.算法时间复杂度的定义?推导时间复杂度?
答:
n是问题输入规模,f(n)是对应的算法基本操作数量,记作O(f(n))。
推导时间复杂度:给一个程序,要会推导它的时间复杂度,见书上例子。

常见时间复杂度:

二、线性表
1.线性表的定义?(逻辑结构上的定义,属于底层)
答:
由零个或者多个数据元素构成的有限序列,就是线性表。序列是有顺序的,并且有限的。

2.线性表的抽象数据类型是什么意思?(底层的接口化,供上层调用)
答:
线性表的抽象数据类型,就是针对线性表这种数据结构,定义一个类,方便程序对线性表的使用。


线性表的抽象数据类型包括两个方面:一个是数据结构本身的定义,一个是定义在该数据结构上的合法操作的具体实现,这里包括创建和初始化列表、判断线性表是否为空、清空线性表、查找元素位置、判断元素是否存在、插入元素、删除元素、线性表长度等操作。
注:对于更复杂的线性表操作,就是更灵活地组合这些基本操作。
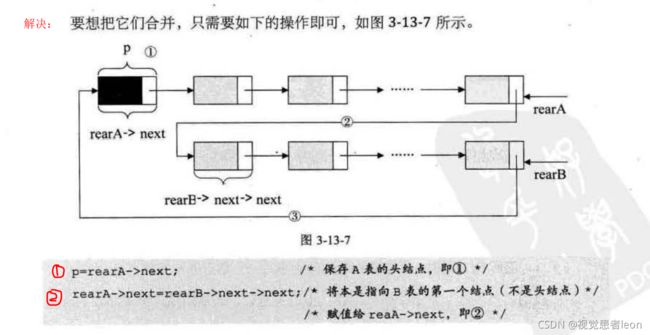
比如,我们需要将线性表A和B进行合并,就是把存在B中但不存在A中的元素,插入到A中。
操作算法为,循环B中每个元素,判断其是否属于A,若不属于,将其插入A中。

3.线性表的顺序存储结构?顺序存储结构下的常用操作:创建,查找,插入,删除等操作?
1)顺序存储结构线性表的创建
答:
线性表的顺序存储结构,其实就是用数组进行实现的。当然,线性表的顺序存储结构与数组有一点区别。
顺序存储结构的线性表包括三个属性:起始存储地址、线性表最大存储容量、线性表当前长度

区别数组长度和线性表长度:
数组长度是在创建线性表时,分配给数组的存储空间长度,就是线性表的最大存储容量,一般后面不再改变。
线性表的长度,是当前线性表中元素的个数,随着线性表的插入和删除操作,这个值一直在变化。
显然,数组长度要大于等于线性表长度。

存储位置关系(地址关系):
假设线性表每个数据元素占用C个存储单元,那么线性表第i+1和第i个数据元素之间的存储位置关系为:

LOC是获取存储地址的函数。

注:顺序线性表的存取操作,时间复杂度为O(1)
C++实现顺序线性表的创建:
bool SqList::CreatList()//创建一个线性表:线性表中的数据元素进行手动输入
{
cout << "输入顺序线性表的长度:" << endl;
cin >> length;//手动输入创建线性表的长度
if (length < 0 || length > MaxSize)
{
cout << "创建失败!线性表的长度不符合要求!" << endl;
length = 0;
return false;
}
cout << "开始创建!" << endl;
for (int i = 1; i <= length; i++)
{
cout << "输入线性表的第" << i << "个元素:";
cin >> data[i-1];
}
cout << "创建完成!" << endl;
return true;
}
2)查找顺序线性表的第i个元素
答:
算法思路:如果线性表不为空,且位置索引i在[1,length]范围,取得第i个元素;否则,获取失败
C++实现获取顺序线性表第i个元素:
bool SqList::GetElem( int i, ElemType *e)//获取线性表的第i个元素 地址传递GetElem( int i, ElemType *e) 引用传递GetElem( int i, ElemType &e)
{
if (i < 1 || i > length || length == 0) //如果线性表为空,或者索引超出范围,获取失败
{
cout << "索引超出线性表范围或者线性表为空" << endl;
return false;
}
else
{
*e = data[i-1]; //类内访问 地址传递是用*e,引用传递时用e
cout << "第" << i << "个元素为:" << *e << endl;
return true;
}
}
3)顺序线性表的插入操作
答:
C++实现顺序线性表在第i个位置插入新元素e:
bool SqList::ListInsert(int i, ElemType &e)
{
if (length == MaxSize)
{
cout << "失败!顺序线性表已满!" << endl;
return false;
}
else if (i < 1 || i > MaxSize) // i索引位置,从1开始
{
cout << "失败!插入位置超出线性表索引范围!" << endl;
return false;
}
else
{
for ( int j = length-1; j >= i-1; j--) //j索引下标,从0开始
{
data[j+1] = data[j]; //元素后移一位
}
data[i - 1] = e;//第i个位置,对应的下标为i-1,插入元素
length++; //插入成功后,线性表长度加1
return true;
}
}
4)顺序线性表的删除操作
答:
C++实现顺序线性表删除第i个位置元素:
bool SqList::ListDelete(int i, ElemType &e)//顺序线性表的删除操作
{
if (length == 0)
{
cout << "线性表为空,无法删除元素!" << endl;
return false;
}
else if (i < 1 || i > length)
{
cout << "删除位置超出线性表长度范围!" << endl;
return false;
}
else
{
e = data[i - 1];//获取删除元素的值
for ( int j = i; j < length; j++)//j索引下标,从0开始
{
data[j - 1] = data[j];
}
length--;
return true;
}
}
注:顺序线性表的插入和删除操作,时间复杂度为O(n)
5)查找顺序线性表是否有某元素,并返回位置i
答:
算法思路:遍历整个顺序线性表,如果当前索引位置的元素与查找元素相同,返回其索引位置i;如果没有,说明无此数据元素
**区分:只返回第一个查找到的元素位置。返回所有查找到的元素位置。**▲▲
C++实现查找顺序线性表是否有元素e,并返回第一个索引位置:
int SqList::LocateElem(ElemType &e)//查找元素,返回索引位置i(只返回查找的第一个位置)
{
for (int i = 1; i <= length; i++)
{
if (data[i - 1] == e)
{
return i; //i表示索引位置,从1开始
}
}
return 0;
}
6)获取线性表的长度
答:
思路:返回当前线性表的length即可。
C++实现获取线性表的长度:
int SqList::ListLength()//获取线性表的长度
{
return length;
}
7)判断线性表是否为空,为满
答:
思路:length =0 表为空;length = MaxSize表为满
C++实现判断线性表是否为空,为满:
bool SqList::ListEmpty()//判断线性表是否为空
{
if (length == 0)
return true;
return false;
}
bool SqList::ListFull()//判断线性表是否为满
{
if (length == MaxSize)
return true;
return false;
}
8)清空顺序表
答:
思路:让length = 0即可
C++实现清空顺序表:
void SqList::ClearList()//清空顺序表
{
length = 0; //让线性表长度为0,即可清空
}
9)显示顺序表
答:
思路:遍历顺序表,打印输出每个元素值
C++实现显示顺序表:
void SqList::DispList()//显示当前顺序表
{
for (int i = 1; i <= length; i++)
{
cout << data[i - 1] << " ";
}
cout << endl;
}
10)合并两个顺序表
1.合并顺序表a和顺序表b =>表c
答:
算法思路:
遍历表a的值,将其全部赋值给c;如果表c的长度超出容量,则合并错误;
否则遍历表b中所有值,如果不属于表a,将其赋值给表c,表c每增加1个元素,长度加1。
C++实现合并顺序表a和顺序表b =>表c:
bool SqList::UnionList(SqList &La, SqList &Lb)//合并表a和表b:对象Lb作为函数参数
{
int i;
for (i = 1; i <= La.length; i++) //允许使用La,Lb的私有属性,因为属于类内访问
{
data[i - 1] = La.data[i - 1];//将表a的数据元素都保存下来
length++;
}
for (int j = 1; j <= Lb.length; j++)
{
if (La.LocateElem(Lb.data[j - 1]) == 0)//如果表a中没有表b的元素
{
if (i < MaxSize)
{
data[i - 1] = Lb.data[j - 1];//只将表b中不同于表a的元素记录下来
length++;
i++;
}
else
{
cout << "表满了,不能再合并!" << endl;
return false;
}
}
}
return true;
}
2.合并顺序表a和顺序表b =>表a
答:
算法思路:
如果表a的长度超出容量,则合并错误;否则遍历表b中所有值,如果不属于表a,将其赋值给表a。
表a每增加1个元素,长度加1。
C++实现合并顺序表a和顺序表b =>表a:
bool SqList::UnionList2(SqList &Lb)//合并表a和表b => 表a:对象Lb作为函数参数
{
for (int i = 1; i <= Lb.length; i++)
{
if(LocateElem(Lb.data[i - 1]) == 0)//如果表a中没有表b的元素 定义成员函数时,可以使用已定义的其他成员函数LocateElem▲▲
{
if (length < MaxSize)
{
data[length] = Lb.data[i - 1];//只将表b中不同于表a的元素记录下来
length++;
}
else
{
cout << "表满了,不能再合并!" << endl;
return false;
}
}
}
return true;
}
3.合并顺序表a和顺序表b =>表b
答:
算法思路:
如果表b的长度超出容量,则合并错误;否则遍历表a中所有值,如果不属于表b,将其赋值给表b。
表b每增加1个元素,长度加1。
C++实现合并顺序表a和顺序表b =>表b:
bool SqList::UnionList1(SqList &Lb)//合并表a和表b => 表b:同一个类,对象Lb作为函数参数,可以使用成员属性▲▲
{
for (int i = 1; i <=length; i++)
{
if (Lb.LocateElem(data[i - 1]) == 0)//如果表b中没有表a的元素
{
if (Lb.length < MaxSize)
{
Lb.data[Lb.length] = data[i - 1];//只将表a中不同于表b的元素记录下来
Lb.length++;
}
else
{
cout << "表满了,不能再合并!" << endl;
return false;
}
}
}
return true;
}
4.线性表的链式存储结构(单链表)?单链表下的常用操作,创建,查找,插入,删除等操作?
答:
单链表定义:
线性表的链式存储结构:使用一段连续或者不连续的存储单元,来存储线性表中的数据元素。存储每个数据元素时,同时存储下一个数据元素的地址。通过地址的连续性表达线性表中数据元素的连续逻辑结构。

单链表的详细理解:头指针、头结点、头结点的数据域和指针域、第一个结点、最后一个结点、最后一个结点的指针域


结点 = 数据域 (当前数据元素值)+ 指针域 (下一个数据元素的存储地址)
这里的数据元素ai是指结点,不仅仅包含数据元素ai的数据域,还包括下一个结点的指针

前奏:
将单链表数据结构,进行抽象数据类型,即定义一个类,用于接口化单链表。包括单链表数据结构的实现、单链表常见合法操作的实现。
**单链表数据结构的实现,就是类的成员属性。单链表常见合法操作的实现,就是类的成员函数。**▲▲▲▲
1)单链表的创建
1.头插法创建单链表
答:
算法思路:
首先建立带头结点的空链表,输入要创建数据元素的个数。
其次循环:创建新结点,对新结点的数据域进行赋值。
插入新结点,首先将新结点的指针域赋值为头结点的指针域,以便将新结点的指针域指向第一个结点。再将头结点的指针域指向新结点,这样便在头结点后面插入了新结点。
最后,头结点的数据域值增加1。
C++实现头插法创建单链表:
template
void LinkList::CreatListHead(int n) //头插法创建单链表
{
for (int i = 1; i <= n; i++)
{
cout << "输入第" << i << "个元素:";
Node *p = new Node; //创建当前结点:每存储一个数据,就要创建一个节点(为什么要在堆区创建数据???)
cin >> p->data; //手动输入
p->next = head->next; //先将插入结点和第一个结点进行连接(如果先连接头结点和插入结点,会丢失第一个节点的地址)
head->next = p; //再将头结点和插入结点进行连接
head->data++; //单链表长度加1
}
}
2.尾插法创建单链表
答:
算法思路:
首先建立带头结点的空链表,输入要创建数据元素的个数。
然后,生成一个结构体指针end,用于指向当前单链表的表尾结点,如果为空表,则指向头结点。
其次循环:创建新结点,对新结点的数据域进行赋值。插入新结点,先将新结点的指针域指向NULL(end->next);再将当前表尾结点的指针域指向新结点(end->next = p);最后,表尾结点就是新结点。
最后,头结点的数据域值增加1。
C++实现尾插法创建单链表:
template
void LinkList::CreatListEnd(int n)
{
Node *end = head; //结构体指针end,控制插入结点与当前尾结点之间的物理结构关系
for (int i = 1; i <= n; i++)
{
cout << "输入第" << i << "个元素:" << endl;
Node *p = new Node; //如果使用Node *p;导致并没有向内存创建结构体变量,报错p是未初始化得到局部变量
cin >> p->data;
p->next = end->next; //end->next其实是NULL:先将end(链表最后一个节点)的指针域保存下来
end->next = p; // 再将链表end节点的指针域,指向插入的“节点的地址”
end = p; //将插入结点变成end(最后一个节点):end是结构体指针,和p指向相同的结点
head->data++;
}
}
2)遍历单链表(显示单链表)
答:
算法思路:
首先,生成一个结构体指针ph,指向当前单链表的头结点。先访问头结点的数据域,取出链表长度,再将结构体指针ph赋值为头结点的指针域,从而指向第一个结点。
循环:只要结构体指针ph的值不为NULL,取出当前指针ph指向的数据域,并将当前指针ph指向下一个节点。
(正常说某个指针指向谁,是说,该指针指向的内容,即数据。除非说,该指针的指向,这就是说该指针本身的值,即地址。当说指针指向的内容时,就是说数据)
C++实现遍历单链表:
template
void LinkList::TraverseList() //遍历单链表
{
Node *ph = head; //头指针:先访问头结点
cout << "单链表长度为:" << ph->data << endl;
ph = ph->next; //访问完头结点,指针指向第一个节点
cout << "单链表中的数据元素为:" << endl;
for (;ph != NULL;ph=ph->next)
{
cout << ph->data << " ";
}
cout << "遍历结束" << endl;
}
3)查找单链表的第i个元素
答:
算法思路:由于不知道第i个元素的地址,只知道头结点的地址,因此需要从头开始找
首先,生成一个结构体指针ph,指向当前单链表的头结点。
然后,判断查找索引值i是否超过单链表长度,如果超过,则查找错误。否则,通过循环,将结构体指针ph指向下一个节点,直到获取第i个数据元素的地址(结构体指针ph指向第i个结点)
最后,通过指针获取数据域。
C++实现查找单链表的第i个元素:
template
bool LinkList::GetElem(int i, ElemType &e)//4.查找单链表的第i个元素
{
Node *ph = head;
//借助head->data
if(i < 1 || i > head->data)
{
cout << "索引位置超出单链表长度范围!" << endl;
return false;
}
else
{
for (int j = 1; j <= i; j++)
{
ph = ph->next;
}
cout << "第" << i << "个元素为:" << ph->data << endl;
e = ph->data;
return true;
}
//不借助head->data
//for (int j = 0; j < i; j++)
//{
// ph = ph->next;
// if (ph==NULL)
// {
// cout << "索引位置超出单链表长度范围!" << endl;
// return false;
// }
//}
//cout << "第" << i << "个元素为:" << ph->data << endl;
//e = ph->data; //当i为0时,返回的是头结点数据域,即链表长度
//return true;
}
注:单链表的查找第i个元素的时间复杂度为O(n)
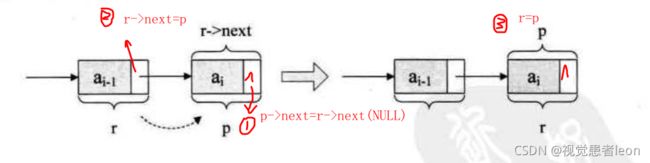
4)单链表的插入操作(在第i个节点位置插入元素e)
答:
要求:插入元素e的结点为s,插入的位置介于结点p和结点p->next之间。
图示: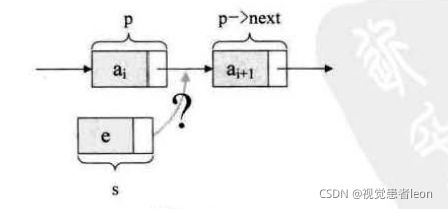
解决思路:先让结点p->next变成结点s的后继结点,再让结点s变成结点p的后继结点。(就是更改结点s和结点p的指针域)
图示:
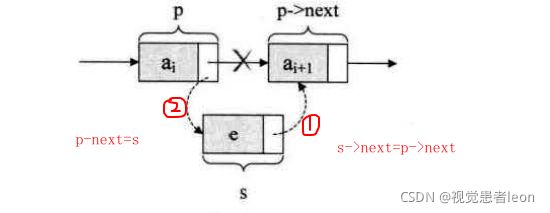
注意:本质就是采用头插法,对于表头和表尾处理相同。(此时是不需要额外的结构体指针指向表尾)
C++实现在第i个节点位置插入元素e:(插入位置i不可以是0)
template
bool LinkList::ListInsert(int i, ElemType &e) //5.单链表的插入操作:第i个节点位置插入元素e
{
Node *p = head; //创建一个结构体指针p,指向头结点,以便遍历单链表
for (int j = 1; j < i; j++) //j < i是为了使得p最终指向第i-1个结点,符合理论
{
p = p->next; //p是当前第j个结点的地址(不包括头结点)
if (p==NULL)//如果p为空,说明p是
{
cout << "插入位置i超出单链表范围!" << endl;
return false;
}
}
Node *s = new Node; //创建新结点
s->data = e;
s->next = p->next; //插入新结点
p->next = s;
head->data++;
cout << "在单链表第i个结点位置,插入成功!" << endl;
return true;
}
5)单链表的删除操作(删除第i个元素):
答:
功能:存储元素ai的结点是p,需要将其删除。
思路:类似于单链表的插入操作,但判断NULL不同,因为表尾下一个位置可以插入元素,但表尾下一个位置不能删除元素。
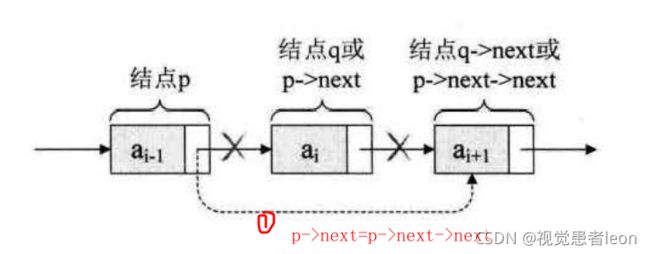


C++实现删除第i个节点位置的元素,并保存给e:(插入位置i不可以是0)
template
bool LinkList::ListDelete(int i, ElemType &e) //6.单链表的删除操作:删除第i个结点位置的元素
{
Node *p = head;
Node *cur; //由于结点都在堆区开辟,需要手动删除,因此需要中间变量结构体指针,用于暂存待删除结点的地址
for (int j = 1; j < i; j++)
{
p = p->next;
if (p->next==NULL) //如果p->next==NULL,说明p是最后一个节点了。如当链表长度为2,要删除的位置为3是,p-next=NULL在j=2时成立,删除位置超出索引范围
{
cout << "删除位置超出索引范围!" << endl;
return false;
}
}
cur = p->next; //待删除结点的地址
e = cur->data; //删除的元素值
cout << "删除的第i个位置的元素值为:" << e << endl;
p->next = p->next->next; //改变p结点指针域,使其指向下下个结点
head->data--;
delete cur;
return true;
}
6)查找单链表是否有某元素e,并返回索引位置
答:
算法思路:
首先创建一个Node结构体指针p,初始化指向头结点。
循环:先使得p = p->next,当p不为空,判断p指向结点的数据域是否等于元素e,若相等,返回当前结点的索引位置。如果不相等,更改p为下一个节点的地址。
C++实现查找单链表是否有元素e,并返回索引位置i:
template
int LinkList::LocateElem(ElemType &e) //8.查找单链表是否有元素e,并返回索引位置i
{
int i = 0;
Node *p = head;
p = p->next;
while (p!=NULL)
{
i++;
if (e == p->data)
{
return i;
}
p = p->next;
}
cout << "单链表没有元素e!" << endl;
return 0;
}
7)查找单链表中间结点,并返回索引位置以及元素值
答:
功能:给定一个带有头结点 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个中间结点。
算法思路:快慢指针法
当用慢指针 slow 遍历列表时,让另一个指针 fast 的速度是它的两倍。
当 fast 到达列表的末尾时,slow 必然位于中间。
template
int LinkList::FindMiddle(ElemType &e)//查找中间结点,将查找的元素值赋给e,并返回该节点是第几个结点,如果是空表则返回0
{
Node *slow, *fast;
slow = head;
fast = head;
int i = 0;
while (fast != NULL && fast->next !=NULL) //结点个数(不包括头结点):当判断fast != NULL,但是fast->next =NULL时,单链表的结点个数是偶数个,如0,2,4,6。
{ //当判断fast = NULL时,单链表的结点个数是奇数个,如1,3,5...。
slow = slow->next;
fast = fast->next->next;
i++;
}
if (fast != NULL && fast->next == NULL) //结点个数为偶数个时,中间结点有两个,选择第二个为中间结点
{
slow = slow->next;
i++;
cout << "单链表中间结点的索引位置为:" << i << endl;
e = slow->data;
cout << "单链表中间结点的元素值为:" << e << endl;
return i;
}
else //结点个数为奇数个时,中间结点只有1个
{
cout << "单链表中间结点的索引位置为:" << i << endl;
e = slow->data;
cout << "单链表中间结点的元素值为:" << e << endl;
return i;
}
}
注:时间复杂度为O(n)
8)逆置单链表
答:
功能:让单链表的表尾结点变成首节点,倒数第二个结点变成第二个结点…第二个结点变成倒数第二个,第一个结点变成表尾结点。
算法思路:
遍历单链表,将每个结点进行头插法,重新插入单链表中。
定义两个结构体指针,一个用于遍历所有结点,一个用于暂存待插入结点。
第一步,先用p指针记录待插入结点的地址。
第二步,断开头结点与第一个结点,就是将单链表置空。
第三步,判断p指向的结点是否为空,如果为空,表示后面没有结点要被插入;否则,暂存当前p指向的结点,就是待插入结点。
第四步,p指针后移,指向下一个节点。
第五步,将暂存结点采用头插法插入头结点后面。
C++实现单链表逆置:
template
void LinkList::ReverseList() //9.逆置单链表
{
Node *p = head, *temp;
p = p->next; //p表示第一个结点的地址,从第一个节点开始遍历
head->next = NULL; //断开头结点和剩余结点的连接,然后开始头插法,重新插入结点
while (p != NULL) //当p不为空,说明没有遍历完单链表
{
temp = p; //先将待插入的结点保存下来(从第一个结点开始)
p = p->next; //更改p的值,使p指向下一个待插入结点:先把后继结点记录下来
temp->next = head->next; //头插法: 插入结点
head->next = temp;
}
}
9)清理单链表,置为空表
答:
算法思路:
首先,创建两个Node结构体指针p、q。p初始化指向头结点。
循环:先使得p = p->next,当p不为空,先将p所指向结点的指针域赋值给q,再执行删除p所指向的结点。
最后将q的值赋值给p,如此循环。
结束循环后,将头结点的指针域置空。
C++实现清理单链表,置为空表 :
template
void LinkList::ClearList() //7.清理单链表,置为空表
{
Node *p = head, *q; //只有new Node才是创建新结点,Node *p只是创建结构体指针,用于指向某个结点
p = p->next;
while (p!= NULL) //表示当前指向的结点,地址不为空
{
q = p->next; //保存待删除结点的下一个节点的地址
delete p; //删除指针p指向的结点
head->data--;
p = q; //新的首节点的地址
}
head->next = NULL; //将头结点的指针域置为NULL
cout << "删除整表成功,已经为空表了!" << endl;
}
总结:单链表一切皆结点,通过结点的地址(指针)来操作结点。创建结点一定会有结点指针,但是创建结点指针不一定会创建新的结点,可能是为了指向已经存在的结点。
5.顺序线性表和单链表优缺点分别是什么?各自适用什么场景?
答:
总结:
顺序线性表,其实就是线性表的数组实现。单链表,其实就是线性表的指针实现。静态链表,就是线性表的游标实现。
顺序线性表优势在于查找方面;单链表的优势在于插入和删除。
另外,如果线性表中的元素变化较大或者不知道有多少元素,用单链表。



6.静态链表的存储结构?静态链表下的常用操作,创建,查找,插入,删除等操作?
答:
静态链表存在意义:对于没有指针或者引用的语言,通过游标来实现单链表功能,显然对于C、C++没什么意义。
静态链表理解:
申请内存时,是一段连续的存储空间,即数组。(数组的下标其实就是地址)
我们定义静态链表的数据结构时,数组的类型是结构体类型,因为数组中的每个元素包括两部分内容,一个是数据,一个是游标。
对于当前的数据元素,它的后继元素可以通过游标指向来找到。
静态链表本质就是把单链表的功能限制在一段连续的存储空间中。
(静态链表是在连续的存储空间内,实现了不连续存储。拥有和单链表一样在插入元素和删除元素的优势,但是不像单链表的内存分配是不受限制,它需要像顺序线性表一样,预先分配一定的内存。)
静态链表定义:
因为有些语言没有指针,所以难以实现普通链表,静态链表就是用来解决这一问题的有力工具,静态链表使用数组来实现链表。
静态链表用游标来代替普通链表的指针域,并且用下标代替普通链表的结点地址。
(1)静态链表的每个结点包含三个要素:下标、数据、游标。
下标表示当前元素所处的位置,类似于链表的结点地址;
游标存放下一个有效结点的下标,类似于链表的指针域。例如下标为2的元素,存放的数据为B,游标值为3,说明下一个结点就是C。
(2)有效结点:含有数据的结点。
(3)第一个结点和最后一个结点不存放数据。
第一个结点(下标为0)存放备用链表的第一个结点的下标;(未被使用的数组元素称为备用链表)
最后一个结点相当于链表的头结点,该结点的游标存放第一个有效结点的下标,当链表为空的时候,游标为0。其他结点的游标都存放下一个结点的下标。
(4)最后一个有效结点的游标为0,说明下一个结点为空。
静态链表下的常用操作,创建,查找,插入,删除等操作?以及对应的C++实现,参考C++实现静态链表
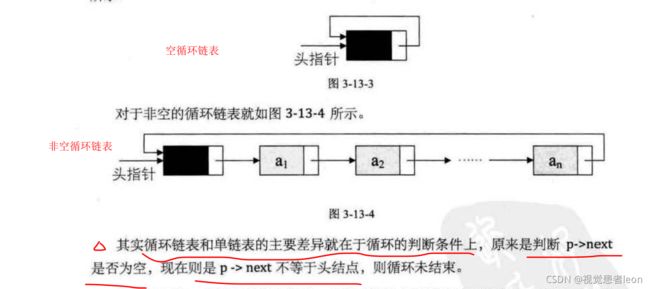
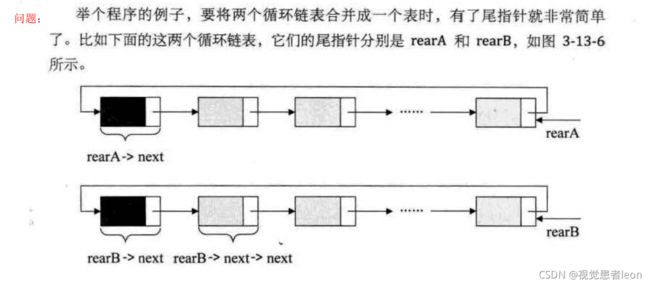
7.循环链表的存储结构?循环链表下的常用操作,创建,查找,插入,删除等操作?
8.双向链表的存储结构?双向链表下的常用操作,创建,查找,插入,删除等操作?
答:
双向链表的存在意义:可以反向遍历查找
双向链表的定义:每个结点有两个指针域,一个指向直接前驱,一个指向直接后继。
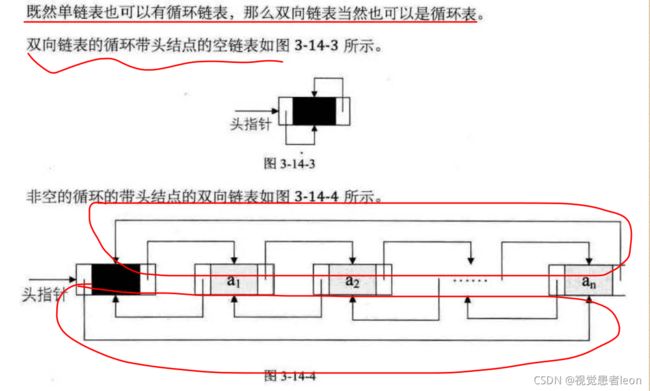
9.线性表的总结
答:
线性表的分类有:顺序表、单链表、静态链表、单向循环链表(循环链表)、双向链表、双向循环链表。
要求:需要明白各自对应的数据结构特点、优缺点(应用场景)。对于顺序表和单链表,要熟练通过C++实现。
三、栈和队列
第一部分:栈
1.栈的定义?(逻辑结构上的定义,属于底层)
答:
栈是一种先进后出(后进先出)的线性表。
栈(stack):是仅在表尾进行插入和删除操作的线性表,因此栈中的数据元素满足前驱后继关系,last in first out线性表,LIFO结构。
栈的应用场景:网页后退功能、编辑文档的撤销功能,满足后来先执行操作。
栈顶(top):允许插入和删除的一端,指线性表的表尾。
栈底(bottom):不允许插入和删除的一端。
空栈:不包含任何数据元素的栈。
栈的插入操作(push):进栈、入栈、压栈。
栈的删除操作(pop):出栈、弹栈。

2.栈的抽象数据类型?(底层的接口化,供上层调用)
答:
由于栈是一种线性表,所以线性表的操作它都具备,但具体操作上不相同,常用包括创建空栈、进栈操作、出栈操作。

3.栈的顺序存储结构?常用操作:创建,插入,删除等操作?
1)创建空栈(包括栈的顺序表数据结构的实现)
答:
思路:
顺序栈使用数组进行实现,数组头为栈底,数组尾为栈顶。包含属性有,栈的存储容量,栈顶指针。
创建空栈时,使得实例化栈对象时,让栈顶指针为-1(在构造函数中实现即可)

//定义顺序栈:抽象数据类型(顺序栈这种数据结构的接口化)
class SqStack
{
public:
SqStack ();
~SqStack ();
private:
ElemType data[MaxSize]; //定义顺序栈的存储结构
int top; //用于栈顶指针(游标作为指针)空栈top=-1,满栈top=MaxSize-1
};
2)进栈操作(插入元素e到栈顶)
答:
思路:
判断是否为满栈,满栈则入栈报错;否则,栈顶指针加1,并将元素插入栈中

C++实现顺序栈的入栈操作:
bool SqStack::push(ElemType &e) //入栈
{
if (top == MaxSize-1) //若满栈,报错
{
return false;
}
else //栈顶指针先+1,再存入元素
{
top++;
data[top] = e;
return true;
}
3)出栈操作(删除栈顶位置的元素)
答:
思路:
判断栈是否为空,若为空,出栈失败;若不为空,删除栈顶元素,用变量e返回删除的元素,栈顶指针减1。
C++实现出栈操作:
bool SqStack::pop(ElemType &e) //出栈
{
if (top == -1) //若栈空,则出栈失败
{
return false;
}
else //若栈不为空,返回删除元素值,栈顶指针减1
{
e = data[top];
top--;
return true;
}
}
总结:
这里说的栈的进栈和出栈操作,其实就是栈的插入和删除操作,但仅仅对当前栈顶位置元素进行的插入和删除。
进栈和入栈的时间复杂度均为O(1)
通过对栈顶指针top的值,可以获取栈中元素个数,是否空栈,满栈等。
4. 两栈共享空间的定义?其顺序表存储结构?常用操作:创建,插入,删除等操作?两栈共享空间的使用场景?
答:
两栈共享空间,即用一个数组存储两个栈。
数组有两个端点,两个栈有两个栈底,让一个栈的栈底为数组的始端,即下标为0;另一个栈的栈底为数组的末端,即下标为n-1。两个栈增加元素时,向数组中间延伸。

使用思路:
栈1的栈顶指针top1,栈2的栈顶指针top2
栈1空:top1=-1
栈2空:top2 = n
栈1空,栈2满:top1=-1, top2=0
栈2空,栈1满:top1=n-1, top2=n
栈满: top1+1=top2,只要满足此式,表示两栈空间满了。
1)创建(包括两栈共享空间的顺序表数据结构的实现)
答:
实例化对象时,通过构造函数创建空栈
// 两栈共享空间:两栈的数据结构的接口化->抽象数据类型
class SqDoubleStack
{
public:
SqDoubleStack();
~SqDoubleStack();
private:
ElemType data[MaxSize]; //两栈共用一个数组
int top1; //栈1栈顶指针
int top2; //栈2栈顶指针
};
//构造函数:两栈为空
SqDoubleStack::SqDoubleStack()
{
top1 = -1;
top2 = MaxSize;
}
2)进栈操作(插入元素e到栈顶)
答:
算法思路:
首先,判断栈是否满,满则不允许插入。不满,判断元素e插入的栈号,再进行元素插入。
C++实现两栈插入操作:
bool SqDoubleStack::push(int StackNumber, ElemType &e)
{
if (top1+1 == top2)
{
return false; // 栈满
}
else
{
if (StackNumber==1) //将元素e插入到栈1
{
top1++;
data[top1] = e;
return true;
}
else if (StackNumber==2) //将元素插入到栈2
{
top2--;
data[top2] = e;
return true;
}
else
{
cout << "栈号输入错误!" << endl;
return false;
}
}
}
3)出栈操作(删除栈顶位置的元素)
答:
算法思路:
首先,根据出栈栈号,判断该栈是否空,空则不允许出栈。不空,则用元素e接收栈顶元素,再将栈顶指针减1
bool SqDoubleStack::pop(int StackNumber, ElemType &e) //出栈操作:元素e接收栈号StackNumber的栈顶元素
{
if (StackNumber==1) //栈1出栈
{
if (top1==-1)
{
cout << "栈1空,无法出栈" << endl;
return false;
}
else
{
e = data[top1];
top1--;
return true;
}
}
else if (StackNumber==2) //栈2出栈
{
if (top2==MaxSize)
{
cout << "栈2空,无法出栈!" << endl;
return false;
}
else
{
e = data[top2];
top2--;
return true;
}
}
else
{
cout << "栈号输入错误!!!" << endl;
return false;
}
}
4)两栈共享空间的使用场景?
答:
事实上,使用两栈共享空间这样的数据结构,通常都是当两个栈的空间需求有相反关系时,也就是一个栈增长时另一个栈在缩短的情况。就像买卖股票一样,你买入时,一定是有一个你不知道的人在做卖出操作。这样使用两栈共享空间存储方法才有比较大的意义。否则两个栈都在不停地增长,那很快就会因栈满而溢出了。
当然,这只是针对两个具有相同数据类型的栈的一个设计上的技巧,如果是不相同数据类型的栈,这种办法不但不能更好地处理问题,反而会使问题变得更复杂,必须要注意这个前提。
5.栈的链式存储结构?常用操作,创建,查找,插入,删除等操作?
答:
链栈:栈顶放在单链表的头部,不需要头结点。对于链栈而言,头指针合并到栈顶指针作用中。


C++实现链栈的数据结构(底层)以及定义一些合法操作:
typedef int ElemType;
class LinkStack //链栈不需要考虑空间
{
public:
struct StackNode //定义新的数据类型:结点作为一个整体,即存储当前数据,也要存储下一个节点的地址,所以用新的数据类型进行封装
{
ElemType data;
StackNode *next;
};
LinkStack();
~LinkStack();
void push(ElemType &e); //1.入栈操作
bool pop(ElemType &e); //2.出栈操作
private:
StackNode *top;
int count; //对于链栈,无法通过栈顶指针获取当前栈数据元素的数量,因此额外添加一个变量count,用于计数
};
1)创建空链栈
答:在实例化对象时,在构造函数中实现
LinkStack::LinkStack() //构造函数:实例化对象,调用构造函数时,创建一个空链栈
{
top = NULL; //top=NULL表示链栈为空(▲在单链表中,头指针为头结点的地址,因此top(head)不为空,因为其指向头结点。而在链栈 中,不存在头结点)
}
2)入栈
答:
算法思路:
不需要判断链栈的空间是否满这个问题。因此创建一个新结点后,将数据存放在这个结点即可,并改变栈顶指针的指向
C++实现入栈:
void LinkStack::push(ElemType &e) //1.入栈操作
{
StackNode *p = new StackNode; //向链栈中插入元素时,需要创建一个新的结点,并返回该节点的地址
p->data = e;//新的栈顶元素
p->next = top;//新栈顶的指针域,指向旧栈顶
top = p; //新的栈顶,为插入结点的地址
}
3)出栈
答:
算法思路:
先判断栈是否空top=NULL,若不空,先改变栈顶指针指向,再删除栈顶结点。
C++实现出栈操作:
bool LinkStack::pop(ElemType &e) //2.出栈操作
{
if (top==NULL)
{
return false;
}
else
{
StackNode *p = top->next; //预存当前栈顶下一个结点的地址(指针)
e = top->data; //获取待删除的数据
cout << e << endl;
delete top; // 释放栈顶空间:手动释放栈顶结点
top = p; //新栈顶
return true;
}
}
4)释放链栈空间
答:
算法思路:
由于链栈中数据元素存放在堆区,需要手动删除
LinkStack::~LinkStack() //手动释放链栈所有结点空间
{
StackNode *p; //预存栈顶下一个节点的地址
while (top!=NULL)
{
p = top->next;
delete top;
top = p;
}
}
6.栈的作用和应用
1)栈的作用
答:
对于栈这种数据结构,如果我们不进行封装,而是每次使用时,都用数组进行实现,那么每次都需要考虑数组下标增减等问题,而忽略了我们使用栈的本意。这对所有数据结构都是类似的道理。
2)栈的应用—递归
1.什么是递归?
答:
斐波那契数列:前面两项之和,等于后一项
(递归的其中一个经典例子)

实现上述功能,可以有两者方法,分别是迭代和递归。
2.递归函数
答:
定义:

注意:递归函数一定要确保不会陷入无限递归中,即当满足一定条件时,不再调用自己,而是返回值退出。
3.递归和迭代的区别
4)栈在递归中的使用
3)栈的应用—四则运算表达式
答:
计算机在对数学表达式进行四则运算时,主要使用后缀表达式。
第一步,先将我们常表示的数学运算式子(中缀表达式:数字在符号两边),转化为后缀表达式(符号在数字后面,并且消除括号)。
第二步,对后缀表达式进行运算。
以上两步,均用栈进行实现。
第二部分:队列
1.队列的定义?(逻辑结构上的定义,属于底层)
答:
队列是一种先进先出的线性表,first in first out,简称FIFO。
队尾:只允许插入
队头:只允许删除
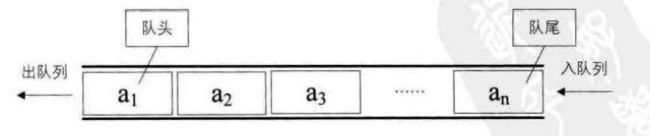
2.队列的抽象数据类型?(数据结构的接口化,供上层调用)
3.队列的顺序存储结构?常用操作:创建,插入,删除等操作?
答:
队列的顺序存储结构,其实使用数组来实现队列这种数据结构。正常情况下,会存在两个问题:
1)如果我们规定队头始终是数组下标为0的位置,那么在进行删除操作时,每删除队头元素,后面所有元素都要向前面移动一位,因此时间复杂度为O(n),所以我们规定队头不一定是数组下标为0的位置。
2)如果我们不规定队头不一定是下标为0的位置,那么当数组前面位置空闲时,我们再次插入元素,此时数组后面已经没有空闲位置了,因此产生假溢出现象。所以,我们将队列的头尾相连接,产生循环队列。
front:指向队头元素位置(游标实现的指针)
rear:若队列不空,指向队尾元素下一个位置(游标实现的指针)
当队列满时,数组中还有一个空闲单元

使用:
1)判断队列空:front == rear
2)判断队列满:(rear+1)%QueueSize = front %是取模或者取余数的意思,Queue是队列所占存储空间
3)求队列长度公式:(rear-front+QueueSize)%QueueSize
4)队尾每插入一个元素时,尾指针rear变动为:rear =(rear+1)%QueueSize,而不是简单的rear=rear+1
4)队头每删除一个元素时,头指针front变动为:front =(front+1)%QueueSize,而不是简单的front=front+1
顺序队列的抽象数据类型(顺序队列的数据结构的接口化)
class SqQueue
{
public:
SqQueue();
~SqQueue();
private:
ElemType data[MaxSize]; //队列存储空间,数组
int front; //头指针:指向队头
int rear; //尾指针:若队列不空,指向队尾下一个位置。若队列空,和front指向同一位置
};
1)创建空队列(初始化顺序队列)
答:
可以在构造函数中,实现创建空队列
SqQueue::SqQueue()
{
front = 0;
rear = 0;
}
2)求队列当前长度
答:
求队列的长度,使用公式(rear-front+QueueSize)%QueueSize
C++实现求队列当前长度:
int SqQueue::QueueLength() //求队列长度
{
return (rear - front + MaxSize) % MaxSize;
}
3)入队列操作
答:
算法思路:
若队列不满,将数据元素e插入队尾;否则,不允许插入。
C++实现入队列:
bool SqQueue::EnQueue(ElemType &e)//enter Queue入队列操作
{
if ((rear+1)%MaxSize == front) //先判断队列是否满
{
return false;
}
else
{
data[rear] = e;
rear = (rear + 1) % MaxSize; //尾指针后移一位:若rear到数组最后,可以通过取余转到数组头部
return true;
}
}
4)出队列操作
答:
算法思路:
若队列不空,删除队头元素,用e返回其值;若队列空,不允许删除。
C++实现出队列操作:
bool SqQueue::DeQueue(ElemType &e) //出队列操作
{
if (front == rear)
{
return false;
}
else
{
e = data[front];
front = (front + 1) % MaxSize;//头指针后移一位:若front到数组最后,可以通过取余转到数组头部
return true;
}
}
总结:
如果不用上面的循环队列实现队列,而是使用简单的顺序表实现队列,删除操作的时间复杂度为O(n),而采用了循环队列后,插入和删除的时间复杂度均为O(1)。
当然,由于循环队列限制了存储空间,所以我们有必要研究不用担心队列长度的链式存储结构。
4.队列的链式存储结构?常用操作,创建,查找,插入,删除等操作?
答:
队列的链式存储结构,就是线性表的单链表,但只能尾进头出,称为链队列。
队头指针,指向链队列的头结点。队尾指针,指向终端结点。(这里和顺序队列是不一样的)

空队列时,front和rear都指向头结点。

注意:
链队列有头结点,而链栈没有头结点,因此在初始化空链栈和空链队列时,是不同的。
一个需要生成头结点,一个不需要生成头结点。生成新结点是需要申请内存空间的。
链队列的抽象数据类型(链队列的数据结构的接口化)
class LinkQueue
{
public:
struct QNode //定义链队列结点的数据类型
{
ElemType data; //结点的数据域
QNode *next; //结点的指针域
};
LinkQueue();
~LinkQueue();
private:
QNode *front; //队头指针
QNode *rear; //队尾指针
};
1)创建空队列(链队列的初始化)
答:
思路:创建头结点,并使得队头指针和队尾指针指向头结点。

C++实现链队列的初始化:
void LinkQueue::InitQueue() //初始化链队列
{
QNode *head = new QNode; //在堆区创建头结点,head指针指向该结点
head->data = 0; //头结点的数据域:计数,结点个数
head->next = NULL;
front = head;
rear = head;
}
2)入队列操作
答:
入队列操作,其实就是在链队列的尾部插入结点。由于是链式存储结构,不用考虑溢出问题。
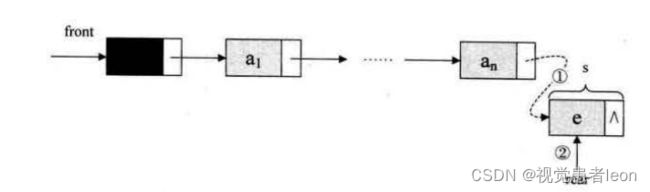
算法思路:创建新节点,更改队尾指针指向,队头指针不用变动。
C++实现入队列操作:
void LinkQueue::EnQueue(ElemType &e) //入队列操作:每次插入一个结点
{
QNode *p = new QNode; //创建新结点
p->next = NULL; //终端结点的指针域为空
p->data = e; //数据存放在结点的数据域
rear->next = p; //插入该结点
rear = p; //更改队尾指针,指向该结点
}
3)出队列操作
算法思路:
首先,判断链队列是否为空,当front=rear时,链队列为空,出队列失败,返回false。
其次当链队列不为空,且只有最后一个结点时,删除结点后,需要将队尾指针指向头结点,即rear = front。
最后,当链队列不为空,且不只有一个结点时,先创建结点指针p,暂存待删除结点的地址;然后更改队头指针,指向待删除结点的后继结点;最后,删除结点。队尾指针不用变动。
C++实现链队列的出队操作:
bool LinkQueue::DeQueue(ElemType &e) //出队列操作
{
if (front==rear) //首先,判断链队列是否为空,若为空,返回false
{
return false;
}
else if (front->next == rear) //其次,判断链队列是否只有一个结点(需要变动队尾指针rear)
{
e = rear->data; //front->next->data
delete rear; //删除最后一个结点 delete front->next
rear = front; //队头指针和队尾指针相同
front->next = NULL;
return true;
}
else//最后,若链队列不只有一个结点(不需要变动队尾指针rear)
{
QNode *p; //先创建一个结点指针p,暂存待删除结点的地址
p = front->next;
e = p->data;
front->next = p->next; //然后,更改头结点的后继结点
delete p; //最后,删除结点
return true;
}
}
4)队列的判空
答:
思路:当队头指针front和队尾指针rear相等时,链队列为空。
C++实现链队列的判空:
bool LinkQueue::IsEmpty() //链队列判空
{
if (front==rear)
{
return true;
}
else
{
return false;
}
}
5)显示队列
答:
算法思路:
首先,判断链队列是否为空,若为空,打印提示队列空语句。
若不为空,定义一个结点指针p,用于遍历所有结点。
C++实现链队列的显示:
void LinkQueue::DispQueue() //显示队列
{
if (front == rear)
{
cout << "链队列是空的!" << endl;
}
else
{
QNode *p;
p = front->next;
while (p != NULL)
{
cout << p->data << endl; //打印当前结点数据域存储的数值
p = p->next; //地址后移
}
cout << "链队列显示完成!" << endl;
}
}
6)查询队列是否有数据元素e,有便返回第一个e的位置
答:
算法思路:
首先,判断链队列是否为空,若为空,打印提示队列空语句。
若不为空,定义一个结点指针p,用于遍历所有结点,若某个结点数据域的值等于查询元素e,返回其位置。
C++实现查询队列是否有数据元素e:
int LinkQueue::LocateElem(ElemType &e) //查询队列是否有数据元素e,有便返回第一个e的位置
{
if (front == rear)
{
cout << "链队列是空的!" << endl;
return 0;
}
else
{
QNode *p;
p = front->next;
int i = 1;
while (p != NULL)
{
if (p->data == e)
{
cout << "链队列有数据元素e,位置为:" << i << endl;
return i;
}
i++;
}
cout << "链队列没有数据元素e!" << endl;
return 0;
}
}
7)计算队列长度
答:
算法思路:
若队列不为空,创建临时结点指针,遍历所有结点,统计结点个数。
C++实现链队列长度计算:
int LinkQueue::GetLength() //获取队列长度
{
if (front == rear)
{
cout << "链队列是空的!" << endl;
return 0;
}
else
{
QNode *p;
p = front->next;
int i = 1;
while (p->next != NULL)
{
i++;
p = p->next;
}
return i;
}
}
8)销毁队列
答:
析构函数:消除链队列的所有结点
思路:
首先,判断链队列是否为空;若不为空,分两次删除,先删除最后一个结点以外的结点,再删除最后一个结点。
LinkQueue::~LinkQueue()
{
if (front == rear) //首先,判断链队列是否为空,若为空,返回false
{
cout << "链队列为空,不用删除!" << endl;
}
else
{
while (front->next != rear) //当链队列不只有1个结点时
{
QNode *p; //先创建一个结点指针p,暂存待删除结点的地址
p = front->next;
front->next = p->next; //然后,更改头结点的后继结点
delete p; //最后,删除结点
}
//删除最后一个结点
delete rear; //删除最后一个结点 delete front->next
rear = front; //队头指针和队尾指针相同
front->next = NULL;
cout << "结点删除完成!" << endl;
}
}
循环队列和链队列的区别和使用场景:
四、串(string)
答:
C++中的string,本质是一个类,本章介绍串的底层封装,是如何形成我们常用的string类。
因此串是一种数据结构,地位等同于顺序表、单链表、顺序栈、链栈、循环队列、链队列等。
小知识点: C语言中的char,char*。C++中的char,char*,string;
解答:
https://www.jianshu.com/p/4db7a5eedc42
C语言中没有字符串这种数据类型,但有两种方法可以表示字符串。
一种是用字符数组,char a[] = “linux”;
一种是字符指针,char *p = “linux”.
char *p=“liunx”; p本身是一个字符指针,占4个字节;“linux”分配在代码段,占6个字节。实际上总共耗费了10个字节。这10个字节,4字节的指针p叫做字符串的指针用来指向字符串(理解为字符串的引子,本身不是字符串);5字节字符内存,才是真正的字符串;最后一个用来存‘\0’的内存是字符串结尾标示(本质也不属于字符串)。
C++实现字符串有两种方法,一种使用C语言中的字符数组,一种是使用string类。
string是一个类,类内部封装了char*,使用字符指针管理这个字符串,是一个char*型的容器。
1.串的定义?(逻辑结构上的定义,属于底层)
答:
串,又叫字符串,string,是有零个或多个字符组成的有限序列。串是一种数据结构。
2.串的抽象数据类型?(数据结构的接口化,供上层调用)
答:串这个数据结构,关注子串的插入,删除、替换、查找等功能,不太关注串中的单个字符。


3.串的顺序存储结构(用数组实现串)
答:
串的顺序存储结构,使用一组地址连续的存储单元,来存储串中的字符序列的。根据预定义的串最大长度MaxSize,每次定义一个串变量(串对象)时,为其分配一个固定的连续的存储单元区域。(这里用定长数组实现)
注:可以使用字符串指针的方式,动态分配字符串的存储空间。char *str = “linux”,str是字符串"linux"的首地址,linux也是顺序存储的,可以通过指针进行访问字符串中的每个数据元素。
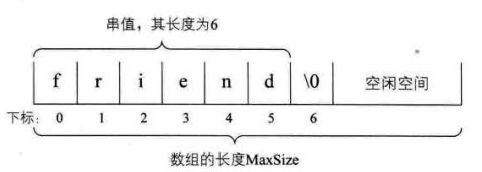
顺序串的抽象数据类型:
class SqString //顺序串:串的顺序存储结构,用数组进行实现
{
public:
SqString();
~SqString();
void Assign(char *s); //初始化,为顺序串赋值
void Show(); //显示字符串:依次输出字符数组每个元素
private:
//两个内置的变量:一个存储字符串的数组 、一个显示数组长度的变量
char str[MaxSize]; //字符数组,用于储存各种ASCII编码的各种字符,如字母、数字、标点符号等
int length; //长度:表示当前数组长度
};
1)顺序串的初始化
答:
串的初始化,就是为串赋值。
C++实现顺序串的初始化:
void SqString::Assign(char *s) //初始化,为顺序串赋值
{
for (int i = 0; s[i] != '\0'; i++) //这里注意:要找到传入的字符串数组中的最后一个元素
{
str[i] = s[i];
length++; //数组长度加1
}
}
2)显示顺序串
答:依次打印字符数组中的每个数据元素
C++实现显示顺序串:
void SqString::Show() //显示字符串:依次输出字符数组每个元素
{
for (int i = 0; i < length; i++)
{
cout << str[i] << " ";
}
cout << endl;
//cout << str << endl; //str最后一个元素不是\0
}
3)获取字符串的长度
答:
string类中的成员属性length,便记录当前字符串的长度。
C++实现获取字符串的长度:
int SqString::GetLength() //获取字符串当前的长度
{
return length;
}
4)删除子串,返回剩余串
从数组中第i个元素开始,删除长度为j的子串(i为子串的首元素),返回剩下的字符串
(其实就是删除字符串中的“第i~第i+j-1"字符,并返回剩余字符串。i的范围为[1,length],j的范围是[1,length-i+1])
第i个元素 = str[i-1]
length = 20 ,字符数组的下标范围为1~19
答:
算法思路:
首先,判断位置i以及长度j,是否满足删除要求。
其次,定义一个字符串对象,用于存储第i位置之前的元素,以及第i+j-1之后的元素。
C++实现截取字符串功能:
SqString SqString::DeleteStr(int i, int j) //删除"第i~第i+j-1"的字符串,返回剩余字符串
{
SqString temp; //用于存储剩余的字符串
if (i > 0 && i<= length && j > 0 && i+j-1 <= length) //i的范围为[1,length],j的范围是[1,length-i+1]
{
int k;
for (k=0; k < i-1; k++) //保留第i元素之前的字符
{
temp.str[k] = str[k];
}
for (k; k + j < length; k++) //保留第i+j-1之后的字符串
{
temp.str[k] = str[k+j]; //忽略k~k+j中的这j个元素
}
temp.length = length - j;
return temp;
}
else
{
cout << "输入不合法" << endl;
return temp;//返回空串
}
}
5)字符串复制
将一个字符串中的所有元素拷贝到另一个字符串数组中
答:
void SqString::StrCopy(SqString &s) //拷贝字符串s,到当前字符串对象中
{
for (int i = 0; i < s.length; i++)
{
str[i] = s.str[i];
}
length = s.length;
}
6)判断两个字符串是否相等
答:
算法思路:
首先,判断两个字符串的长度是否相等,若不相等,返回false。
其次,判断两个字符串的每个数据元素是否相等,有任何一个不相等,返回false。否则,返回true。
C++实现判断两个字符串是否相等:
bool SqString::IsSame(SqString &s) //比较当前字符串和s字符串是否相等
{
if (length != s.length) // 先判断两个字符串的长度 (为什么可以使用s的私有属性)
{
return false;
}
else
{
for (int i = 0; i < length; i++) //再依次判断字符串的每个字符
{
if (str[i] != s.str[i])
{
return false;
}
return true;
}
}
}
7)连接两个字符串
答:
算法思路:
首先,判断两个字符串的长度之和是否超过字符串预定义的最大长度,若超过,提示连接失败。
其次,实例化一个新的空字符串,将这两个字符串依次存储到这个空字符串中,返回新字符串。
C++实现连接两个字符串:
SqString SqString::Concat(SqString &s) //连接两个字符串
{
SqString temp;
if (length + s.length > MaxSize)
{
cout << "超过最大长度!" << endl;
return temp;
}
else
{
int i = 0;
for ( ; i < length; i++)
{
temp.str[i] = str[i];
}
for (int j = 0; j < s.length; j++)
{
temp.str[i + j] = s.str[j];
}
temp.length = length + s.length;
return temp;
}
}
8)获取子串
(获取数组中第i个元素开始,长度为j的子串)
答:
第i个元素,指的是第i个位置,从1开始,即对应字符数组下标[i-1]
算法思路:
首先,判断子串首末位置是否在当前串中。(i<0 || i>length; j<0 || i+j-1>length 四个条件中任何一个满足,获取子串失败,返回空串)
其次,将该子串存储到新的字符串对象中,并返回。
C++实现获取子串:
SqString SqString::GetSub(int i,int j) //获取字符串s中的子串
{
SqString temp;
if (i<0 || i>length || j<0 || i+j-1 > length)
{
cout << "子串不在要求位置!" << endl;
}
else
{
for (int k=0; k < j; k++)
{
temp.str[k] = str[k + i - 1];
temp.length++; //长度要记得累加
}
}
return temp;
}
9)插入字符串
(在字符串第i个位置,插入一个新的字符串,返回插入后的字符串)
答:
算法思路:
首先,判断待插入字符串长度和当前串长度之和,是否超过最大串长度。若超过,提示插入失败,返回空串。
否则,在新的字符串对象中,存储当前字符串和待插入串,并返回新串。
C++实现插入字符串:
SqString SqString::InsertStr(int i, SqString &s)//字符串插入:将字符串s插入到当前串中
{
SqString temp;
if (length + s.length > MaxSize)
{
cout << "超过串最大长度!" << endl;
}
else
{
for (int k = 0; k < length + s.length; k++)
{
if (k < i) //0~i-1 (在第i个元素位置之后插入,说明前面有i个元素)
{
temp.str[k] = str[k];
}
else if (k < i+s.length) //插入字符串s
{
temp.str[k] = s.str[k - i];
}
else
{
temp.str[k] = str[k - s.length]; //插入剩余字符串
}
temp.length++;
}
}
return temp;
}
10)替换子串
(将数组中的第i个元素开始,长度为j的子串,替换成指定字符串t)
答:
算法思路:
首先,判断子串首末位置是否在当前串中(i<0 || i>length; j<0 || i+j-1>length ),以及插入字符t后是否超过串最大长度(t.length + length - j > MaxSize),有一个条件满足,替换失败
其次,将当前串的指定位置替换为字符串t,并返回新串。
C++实现替换子串:
SqString SqString::ReplaceStr(int i, int j, SqString &t) //替换子串:将数组中的第i个元素开始,长度为j的子串,替换成指定字符串t
{
SqString temp;
if (i<0 || i>length || j<0 || i + j - 1 > length || length-j+t.length > MaxSize)
{
cout << "替换失败!" << endl;
}
else
{
for (int k = 0; k < length-j+t.length; k++)
{
if (k < i)
{
temp.str[k] = str[k];
}
else if(k < i+t.length)
{
temp.str[k] = t.str[k - i];
}
else
{
temp.str[k] = str[k - t.length + j];
}
temp.length++;
}
}
return temp;
}
11)索引子串位置
答:
在主串s第pos个位置之后,若主串s中存在某个子串等于串值T,返回其在pos位置之后,第一次出现的索引值,即串T首字符在主串中的索引位置。(索引从1开始)
详细见“串的模式匹配”问题。
朴素方法算法思路:
首先,判断pos位置是否符合主串T的范围,以及pos位置之后,主串的剩余长度是否大于子串T的长度。
其次,以pos位置后第一个元素开始,与子串T进行匹配,只要一个字符不相等,开始下一次匹配。
(对主串pos后面的每个字符作为大循环,以每个字符往后T长度作为小循环,直到匹配成功或遍历结束。)
C++实现顺序串的朴素方法解决子串索引问题:
int SqString::IndexSub(int pos, SqString &s) //搜索主串中pos位置之后,与串s相等的子串位置。
{
if (pos<0 || pos >length || pos+s.length > length) //pos = 1~length
{
cout << "超过索引范围!" << endl;
return 0;
}
for (int i = pos; i < length - s.length; i++) //大循环
{
for (int j = 0; j < s.length; j++) //小循环
{
if (str[i + j] != s.str[j])
{
break;//匹配过程中,只要有1个字符不相等,就开始下一次匹配(跳出小循环,大循环继续)
}
if (j == s.length - 1) //当j的值等于s.length-1,说明每个字符都相等,匹配成功
{
cout << "匹配成功!" << endl;
return i + 1; //返回索引位置
}
}
}
return 0; //大循环结束后,仍然没有搜索到
}
12)字符串比较大小
答:

算法思路:
首先,比较两个字符串长度,谁长谁大。当前串大,返回1,串s大,返回-1。
其次,依次比较每个字符的ASCII码,当前串大,返回1;串s大,返回-1;两串相等,返回0。
C++实现字符串比较:
int SqString::StrCompare(SqString &s) //比较字符串大小
{
if (length > s.length)
{
return 1;
}
else if (length < s.length)
{
return -1;
}
else
{
for (int i = 0; i < length; i++)
{
if (int(str[i]) > int(s.str[i]))
{
return 1;
}
else if(int(str[i]) < int(s.str[i]))
{
return -1;
}
}
return 0;
}
}
总结:关于子串的操作,如 4, 8,9, 10,11思路类似,其实11是重中之重。
4.串的链式存储结构(用指针实现串)
答:
串的链式存储结构,每个结点的数据域是字符,一个结点可以存放一个字符,也可以存放多个字符。

最后一个结点如果没有占满,可以用“#”补全。

串的链式存储结构,其实指的就是封装好的字符串类型string。
串的顺序存储结构,其实是我们常见的字符数组char[]
5.串的模式匹配(字符串查找):解决子串的定位问题
1)朴素方法
答:
时间复杂度高,算法低效。
2)KMP方法
答:推导过程见大话数据结构。
算法原理:
主串S,子串T两者在匹配时,主串的索引位置i不会回溯,即不会减小。
而子串的索引位置j,当发生不匹配时,根据当前子串的索引位置,由next数组确定下一次开始的地方。
问题的关键是确定子串中,是否有与首字符重复的字符,并确定其位置。
实现过程:
1.先求出模式串(子串)的next数组
2.在主串和模式串进行匹配时,根据next数组进行回溯。
五、树
1.树的定义
总结:
根据树的定义,可见对于树这种结构,使用顺序存储和链式存储这种一对一线性存储方式,很难实现树的一对多结构。
为此,提出三种新的存储结构:双亲表示法、孩子表示法、孩子兄弟表示法
2.树的抽象数据类型
答:主要介绍树这种数据结构,其底层的存储结构是什么,以及常用的操作有哪些。

3.树的存储结构(底层的存储结构)
答:主要介绍思路(结合顺序存储结构和链式存储结构方法)
1)双亲表示法
答:
思路:每个结点都有唯一的双亲,因此在记录结点时,可以同时记录该结点双亲的位置。
(定义新的数据类型,结点数据类型,由数据域和指针域组成,指针域是当前结点的双亲位置,用数组下标表示。
这里用一组连续地址空间存储结点,因此记录双亲位置的指针域,用数组下标记录。本质上是顺序存储方式)
结构图、底层结构代码表示、改进方法、优缺点(见书本)。
2)孩子表示法
答:
思路:记录结点中数据域的同时,记录该结点的每个孩子的位置,即有多个指针域。
(顺序存储+链式存储)
结构图、底层结构代码表示、改进方法、优缺点(见书本)。
3)孩子兄弟表示法
答:
思路:记录结点中数据域的同时,记录结点的第一个孩子和右兄弟这两个位置,即包含两个指针域。
(将复杂树变成二叉树,充分利用二叉树的特性和算法)
(链式存储)
结构图、底层结构代码表示、改进方法、优缺点(见书本)。
4.二叉树的定义
答:


特殊二叉树:
1)斜树:每一层都只有1个结点
2)满二叉树:所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上。
3)完全二叉树:对于某个二叉树,其结点编号和满二叉树结点编号相同,它就是完全二叉树
5.二叉树的性质
答:理解并记忆
![]()
![]()
![]()
n0 = n2 + 1 (利用分支连接线总数和结点数的关系进行推到)

(利用完全二叉树的结点数目,少于同样深度数k的满二叉树,但大于同样深度数k-1的满二叉树)
6.二叉树的存储结构
1)顺序存储
答:
由于完全二叉树的结点编号是连续的,因此可以用数组进行存储。
对于非完全二叉树,不连续结点占领存储空间,但不存储实际数据。
2)链式存储(重点)
答:
对于二叉树每个结点,最多只有两个孩子,因此每个结点设计一个数据域和两个指针域,两个指针域分别指向左孩子和右孩子地址,此种存储方式叫二叉链表。如果在指针域,再增加一个指向双亲位置的指针,就叫三叉链表了。
7.二叉树的遍历
主要讲解原理
1)什么是二叉树的遍历
答:

访问就是对所有结点的一种操作,比如打印所有结点存储的数据信息。
次序就是,树结构不同于线性结构,其不止一种前驱后继的关系,因此不同的次序,使得访问结点的顺序不一样。
还有一个重要信息,就是无论采用什么遍历方式,都是从根节点开始找各个节点。即便对于后序,也是通过根节点找到其他结点,先处理其他结点,最后再处理根节点。对于二叉树的建立,同样如此,无论采用前中后哪种次序建立二叉树,都要从根节点出发,来找到其他结点。
之所以可以使用这种方式,是因为采用递归的方式进行了解决。
以前序为例:一开始传入的是根节点,我们先处理根节点,然后处理左孩子结点,最后处理右孩子结点。在处理左孩子结点时,遵从和处理根节点相同的道理,先处理当前结点,再处理其左孩子结点,最后处理右孩子结点。当处理的某个结点的地址为NULL时,表示不需要再处理他的左孩子右孩子了。
对于根节点来说,其实就是一个函数,先处理自己,再处理他的左孩子结点,再处理右孩子结点。只不过在处理两个孩子结点时,使用了同样的函数,即递归。
以中序为例:一开始传入的是根节点,我们先处理左孩子结点,然后处理根节点,最后处理右孩子结点。只不过在处理左孩子结点时,再次使用当前定义的函数,先处理左,再中,最后右,如此嵌套。
2)二叉树的遍历方法
1.前序遍历
答:
首先,访问根节点开始;
其次,遍历根节点的左子树(从上到下,所有结点的左优先,再访问右结点,然后回溯)。
最后,遍历根节点的右子树
2.中序遍历
答:
首先,从根节点的左子树开始(从最左边叶子结点开始,从下往上,然后访问右结点)
其次,访问根节点
最后,遍历根节点的右子树

3.后序遍历
答:
首先,从根节点的左子树开始(从最左边叶子结点开始,然后访问右结点,从下往上)
其次,遍历根节点的右子树
最后,访问根节点
4.层序遍历
答:
首先,从根节点开始。
其次,从上往下,逐层访问(每一层按从左到右顺序)
总结:不同遍历方法的意义?
答:
二叉树的遍历,将树结构中的结点变成线性序列,方便程序处理
3)遍历算法实现
答:
由于二叉树的定义,使用递归的方式,因此要完成对二叉树的遍历,使用递归函数实现。过程见书本
前序
中序
总结:根据两种遍历顺序,确定二叉树结构,从而得到另外一种遍历顺序(推导见书本)
前序+中序 => 后序
后序+中序 => 前序
前序+后序 !=> 不能确定二叉树结构,从而得不到中序
8.二叉树的建立
答:
使用二叉链表这种数据结构实现二叉树的建立,对于使用前序,中序,后序,创建二叉树的的代码略有区别。
(二叉链表:一个数据域,两个指针域)
思路:
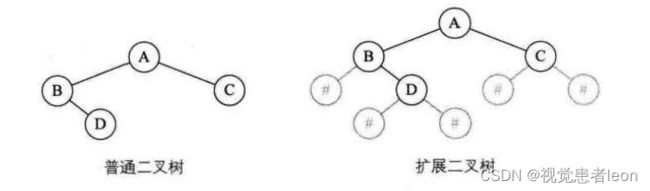
首先将二叉树扩展为均有左右孩子,对于二叉树中每个结点的空指针,引出一个虚结点,其存储的值为“#”。对于这种扩展二叉树,一个遍历顺序就可以确定一棵树的结构。
建立二叉树,也使用了递归原理,只是将原来打印结点的地方,改成创建结点并赋值的操作。
9.二叉树的链式存储结构?创建,查找,插入,删除等操作?
1)二叉链表的抽象数据类型(数据结构的接口化,供上层调用)
答:
typedef char ElemType;
class LinkBiTree
{
public:
struct BiTreeNode //定义新的数据类型:二叉链表的结点
{
ElemType data; //当前结点的数据域
BiTreeNode *lchild, *rchild; //当前结点的指针域:指向左孩子和右孩子
};
LinkBiTree();
~LinkBiTree();
void Init_PreCreateBiTree(); //前序创建二叉树接口模块:调用私有成员函数,前序建立二叉树函数(由于二叉树建立使用了类的私有成员属性,因此这里在类内定义接口,调用私有成员函数创建二叉树)
void De_PreReleaseBiTree(); //销毁前序创建的二叉树的接口模块:调用私有成员函数,销毁前序创建的二叉树,该函数为接口,功能实现见 PreReleaseBiTree(BiTreeNode *bt)
void Port_PreOrder(); //前序遍历接口模块
void Port_InOrder();//中序遍历接口模块
void Port_PostOrder();//后序遍历接口模块
private: //二叉树在私有权限,和前面提到的数据结构有很大不同,主要原因是用到了递归这种函数
BiTreeNode *root; //头指针,指向根节点
BiTreeNode * PreCreateBiTree(BiTreeNode *bt); //使用前序建立二叉树:输入二叉树的前序序列,创建结点用于存储(返回值是创建结点的地址)
void PreReleaseBiTree(BiTreeNode *bt); //销毁前序创建的二叉树
void PreOrder(BiTreeNode *bt);//前序遍历二叉树
void InOrder(BiTreeNode *bt);//中序遍历二叉树
void PostOrder(BiTreeNode *bt);//后序遍历二叉树
};
2)二叉树的建立
答:在创建二叉链表时,根据采用前序、中序、后序创建二叉树的不同,二叉树结构对应的序列也需要按照相同方式输入。
如采用前序创建二叉树时,键盘输入的序列是二叉树的前序遍历才行。
1.前序创建二叉树
答:
前提:按照二叉树的前序遍历形成的字符序列输入
算法思路:
1,判断当前输入的字符是否为#,是则表示当前结点为虚结点,结点地址(指针)为NULL,不用创建结点空间;
2,若不是,则创建结点空间,存下数据。
3,使用1和2创建其左孩子,再创建右孩子。如此嵌套。
4,最后返回该结点的指针。
C++实现前序创建二叉树:功能实现放在类的私有权限,接口实现放在公共权限,以便调用。
LinkBiTree::BiTreeNode * LinkBiTree::PreCreateBiTree(BiTreeNode *bt) //使用前序建立二叉树:输入二叉树的前序序列,创建结点用于存储
{
ElemType elem; //输入的字符
cin >> elem;
if (elem == '#') //如果当前结点存储的数据域为#,那么此结点为虚结点,指向该结点的指针为空指针
{
cout << "当前结点为虚结点!" << endl;
bt = NULL; //如使用函数PreCreateBiTree(root),如果输入的第一个字符为#,那么根节点为虚结点,即头指针为空指针
}
else
{
bt = new BiTreeNode;//如果当前结点存储的数据域地址不为#,是字符,创建结点空间
bt->data = elem; //存下数据
cout << "打印当前结点的数据域:" << bt->data << endl;
bt->lchild = PreCreateBiTree(bt->lchild); //当前结点的左孩子地址:如果左孩子是虚结点,即输入#,那么bt->lchild = NULL;如果左孩子不是虚结点,假设输入b,递归函数会创建一个新的结点,存储b,并返回该结点指针(地址),如此循环递归
bt->rchild = PreCreateBiTree(bt->rchild);
//对于前序,先根节点,在左子树,后右子树
}
return bt;
}
void LinkBiTree::Init_PreCreateBiTree()//调用私有成员函数:前序建立二叉树函数
{
PreCreateBiTree(root); //头指针始终存在,不管有没有根结点。当根节点存在时,创建根节点存储空间,并用头指针指向它
cout << "前序创建二叉树完成!" << endl;
}
2.中序创建二叉树
3.后序创建二叉树
3)二叉树的销毁
答:根据创建二叉树采用的遍历顺序不同,采用相应的销毁顺序。
1.销毁前序遍历创建的二叉树
答:
思路:当前结点不是虚结点时(即该结点的指针不是NULL),销毁其左孩子,再销毁其右孩子。最后,销毁该结点。
C++实现销毁前序遍历创建的二叉树:
void LinkBiTree::PreReleaseBiTree(BiTreeNode *bt) //销毁前序创建的二叉树
{
if (bt != NULL)
{
PreReleaseBiTree(bt->lchild);
PreReleaseBiTree(bt->rchild);
delete bt;
}
}
void LinkBiTree::De_PreReleaseBiTree() //调用私有成员函数://销毁前序创建的二叉树,该函数为接口
{
PreReleaseBiTree(root);
cout << "销毁前序创建的二叉树!" << endl;
}
2.销毁中序遍历创建的二叉树
3.销毁后序遍历创建的二叉树
4)二叉树的前序遍历
答:
思路:
先根结点,再左子树,后右子树。(先结点,再左孩子,后右孩子)
void LinkBiTree::PreOrder(BiTreeNode *bt)//前序遍历二叉树
{
if (bt == NULL)
{
cout << "#" << endl;
}
else
{
cout << bt->data << endl;
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
void LinkBiTree::Port_PreOrder()
{
PreOrder(root);
cout << "前序遍历结束!" << endl;
}
5)二叉树的中序遍历
答:
思路:
先左子树,再根结点,后右子树。(先左孩子,再结点,后右孩子)
void LinkBiTree::InOrder(BiTreeNode *bt)//中序遍历二叉树
{
if (bt == NULL)
{
cout << "#" << endl;
}
else
{
InOrder(bt->lchild);
cout << bt->data << endl;
InOrder(bt->rchild);
}
}
void LinkBiTree::Port_InOrder()
{
InOrder(root);
cout << "中序遍历结束!" << endl;
}
6)二叉树的后序遍历
答:
思路:
先左子树,再右子树,后根结点。(先左孩子,再右孩子,后结点)
void LinkBiTree::PostOrder(BiTreeNode *bt)//后序遍历二叉树
{
if (bt == NULL)
{
cout << "#" << endl;
}
else
{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout << bt->data << endl;
}
}
void LinkBiTree::Port_PostOrder()
{
PostOrder(root);
cout << "后序遍历结束!" << endl;
}
7)二叉树的高度
10.线索二叉树的链式存储结构?创建,查找,插入,删除等操作?
1)什么是线索二叉树?
答:
针对二叉链表实现二叉树时,存在许多空指针域浪费内存空间的问题,提出让结点的lchild指针域指向当前结点的前驱结点位置,让rchild指针指向当前结点的后继结点位置。这种二叉树叫线索二叉树。
(由于将二叉树按照某种遍历方法,形成的序列,此时结点的前驱和后继就唯一了,因此这里结点的前驱和后继不是指树结构中的,而是指树结构以前序或中序或后序遍历形成的序列)
问题:某一个结点的lchild是指向它的左孩子还是前驱?rchild是指向它的右孩子还是后继?
解决:增加两个标志域,ltag和rtag,布尔型变量,0或1.

总结:
线索化的实质,是将二叉链表中的空指针改为指向前驱和后继的线索。
由于前驱和后继是针对二叉树的某个遍历方法而言的,因此线索化的过程,就是在遍历二叉树的过程中,不断修改空指针。
线索二叉树使用场景:使用二叉树这种结构时,当经常遍历或者查找结点的前驱和后继时,采用这种结构。
2)线索二叉树的抽象数据类型(数据结构的接口化,供上层调用)
11.二叉树、树、森林之间的相互转化
答:
具体参考书本,内容包括树=>二叉树,森林=>二叉树,二叉树=>树,二叉树=>森林,以及树和森林的遍历。
12.哈夫曼树
六、图
1.图的定义
2.图的抽象数据类型(定义常用的合法操作)
3.图的存储结构
答:介绍图这种数据结构,它的底层存储结构是如何实现的。
1)邻接矩阵
(两个数组:一个一维数组存储顶点,一个二维数组存储顶点之间的边)
2)邻接表
为了解决邻接矩阵在存储边表存在空间浪费的问题
(一个链表或数组,用于存储顶点和顶点的第一个邻接点地址;另一个链表用于存储当前顶点的所有边)
3)十字链表
对于有向图,为了解决邻接表只关心出度,逆邻接表只关心入度的问题
(将邻接表和逆邻接表,功能整合在一起)
4)邻接多重表
对于无向图,解决关注对边的操作问题,改进邻接表存储结构
5)边集数组
关心对边的操作
(两个数组:一个一维数组存储顶点,一个一维数组存储一条边的起点下标,终点下标,权值)
4.图的遍历
1)深度优先遍历
2)广度优先遍历
图的应用
5.最小生成树
答:包含图中所有顶点,形成一个连通图对于包含权值的网图,我们构造连通图的最小代价生成树,就是最小生成树存在两种算法,分别为普里姆算法和克鲁斯卡尔算法。
1)普里姆算法
2)克鲁斯卡尔算法
6.最短路径
答:求两个顶点之间最短的路径。两种方法
1)迪杰斯特拉算法
2)弗洛伊德算法
7.拓扑排序
答:顶点之间必有优先顺序,对有向图进行顺序构造,就是拓扑排序。
8.关键路径
答:完成项目工程的最短时间
七、查找算法
答:
查找(Search)定义:输入某个值,在查找表中确定一个数据元素(记录),其某个数据项(关键字)等于要查询的值。
(注:数据元素包含多个数据项,对于数据元素只包含一个数据项时,如查找数组中是否有某个数字,我们可以返回其下标位置)
关于查找的几个概念:(参考书)
1.查找表:由同一类型的数据元素(记录)构成的集合。
2.关键字:数据元素中某个数据项的值。=> 关键码,主关键字,主关键码,次关键字,次关键码

3.静态查找表:只允许查找操作的查找表
4.动态查找表:在查找时,插入查找表中原本不存在的数据元素,或者删除查找表中已经存在的数据元素。
5.查找结构:

1.顺序表查找
答:
定义:对于用数组实现的顺序表,从表中第一个数据元素开始查找,直至遍历整个查找表。算法复杂度为O(n)
查找表要求:顺序(数组形式的连续内存),但可以不有序(升序或降序),可以有重复元素
1)基本算法(重点)
int SqList::SqSearch1(ElemType &e)//查找元素,返回索引位置i(只返回查找的第一个位置)
{
for (int i = 1; i <= length; i++)
{
if (data[i - 1] == e)
{
return i; //i表示索引位置,从1开始
}
}
return 0;
}
2)优化算法
思路:设置哨兵:如果a[1]~a[length-1]中有查找值e,返回索引位置。否则,返回0,因为a[0]肯定等于e,表示查找失败。
优点是避免每次判断i是否越界,减少语句i2.有序表查找
1)二分查找
1.查找条件
答:查找表采用顺序存储(数组存储),并且有序(如从小到大),没有重复的数据元素。
2.查找思路
答:
首先,定义初始查找表范围,每次查找时,判断区间是否存在。
然后,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功。
若给定值小于中间记录的关键字,更新右边界,并在中间记录的左半区继续查找。
若给定值大于中间记录的关键字,更新左边界,并在中间记录的右半区继续查找。
最后,不断重复上述过程,直到查找成功,若所有查找区域无记录,查找失败为止。
关键:
1.定义好目标值所在的区间,一般为双闭区间
2.更新左边界或右边界
3.算法实现
答:
(重点):定义查找值target在一个左闭右闭的封闭区间,也就是[left, right]。

class Solution
{
public:
int search(vector& nums, int target)
{
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) // 当left==right,区间[left, right]依然有效,所以用 <=
{
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target)
{
right = middle - 1; // target 在左区间,所以[left, middle - 1]
}
else if (nums[middle] < target)
{
left = middle + 1; // target 在右区间,所以[middle + 1, right]
}
else // nums[middle] == target
{
return middle; // 数组中找到目标值,直接返回下标
}
}
return -1; // 未找到目标值
}
};
定义查找值target在一个左闭右开的区间,也就是[left, right)。即target只能取到right-1
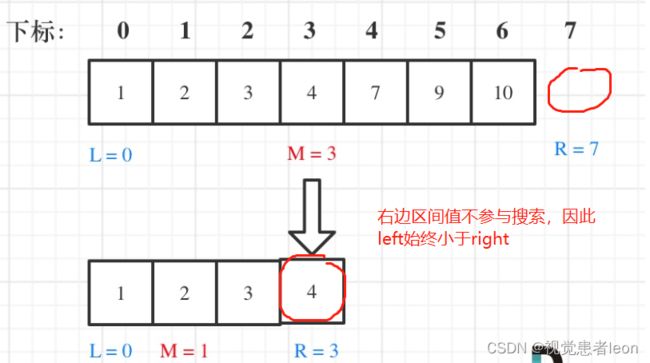
class Solution
{
public:
int search(vector& nums, int target)
{
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,其实仍然在搜索0~nums.size()-1空间,即:[left, right)
while (left < right) // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
{
int middle = left + ((right - left) >> 1); //mid=(left+right)>>1相当于mid=(left+right)/2,但是比除2运算要快
if (nums[middle] > target)
{
right = middle; // target 在左区间,在[left, middle)中,下一个查询区间不会去比较nums[middle]
}
else if (nums[middle] < target)
{
left = middle + 1; // target 在右区间,在[middle + 1, right)中
}
else // nums[middle] == target
{
return middle; // 数组中找到目标值,直接返回下标
}
}
return -1; // 未找到目标值
}
};
4.优缺点
答:
二分查找的次数最多为树的深度,最少为1次,因此时间复杂度为O(logn)。
优点是显然查找速度相比于顺序查找提高很多。
缺点是查找表需要满足有序且数据元素无重复的要求。
5.使用场景
答:适用静态查找表,不适合动态查找表。
![]()
2)插值查找
答:
思路:在二分查找基础上进行改进,将二分查找中的1/2进行更改,使用插值公式(根据最大值、最小值、查找值进行计算得到)
实现:
![]()
要求:对于有序且无重复的查找表,数据分布均匀可以使用,效率比二分查找更高,但不均匀分布的数据集合不能使用。
3)斐波那契查找
3.哈希表查找(散列表查找)
1)基本概念
1.哈希表的定义
答:
顺序表和有序表查找:通过比较查找值和查找表中数据元素是否相等,得到索引位置或存储位置
哈希表:根据查找值,通过一个函数,直接映射得到索引位置。存储位置 = f(查找值)
f是哈希函数或者散列函数,哈希表或者散列表的存储地址是连续的,数据元素存储的位置叫散列地址。
2.哈希表的查找步骤
答:其实就两步。
存储时,根据散列函数,计算出数据元素的存储地址进行存储。
查找时,根据散列函数,计算出数据元素的存储地址进行查找。
注:
散列技术既是一种存储技术,也是一种查找技术。
散列表中的数据元素之间,不像线性表、树、图那样存在前驱后继的逻辑关系,数据元素彼此之间没有逻辑关系。
散列表中数据元素(关键字)只与它的存储位置有关系,这个关系就是散列函数。
散列表是一种面向查找的数据结构,O(1)的查找时间复杂度。
3.哈希表查找的优缺点
答:
优点:善于查找与给定值相等的问题。
缺点:若查找值对应多个结果,不适合。范围查找也不适合。

给一个查找表,一个要查找的关键字,哈希表为什么查找会很快?
因为能进行哈希查找的前提是,我们构建了哈希表。也就是我们对原来的查找表进行了重新设计,使得查找表中的元素与索引位置有固定的映射关系。因此,我们牺牲了空间,换来了时间效率。
4.哈希表设计中的关键问题
答:
第一个是散列函数如何设计?
第二个是当不同的关键字,对应相同的存储位置,该如何解决?(冲突问题)
2)散列函数的设计
答:
确定映射关系,根据关键字,可以得到对应的散列地址。(这种映射关系得到的散列地址一定是连续的吗?)
设计散列函数的原则:计算简单、得到的散列地址分布均匀。
几种常用散列函数:
1.直接地址法(重点)
取关键字的某个线性函数值,作为散列地址。f(key) = a*key+b
特点是散列函数简单,得到的散列地址分布均匀,不会产生冲突。但需要事先知道关键字的分布情况,适合查找表较小且连续的情况。
2.数字分析法
抽取关键字的一部分来计算散列地址。
特点是适合处理关键字位数比较大,事先知道关键字的分布且关键字的若干部分分布均匀。
3.平方取中法
对关键字进行平方,然后使用中间部分作为散列地址。
特点是适合不知道关键字的分布,而位数不是很大的情况。
4.折叠法
将关键字从左到右分割成位数相等的几部分(注意最后一部分位数不够时可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。
特点是事先不需要知道关键字的分布,适合关键字位数较多的情况。
5.保留余数法(重点)
用关键字除以某个值,得到的余数作为散列地址。对于散列表长为m,f(key) = key mod p ,p<= m,mod是求余数、取模的意思。
若散列表表长为m,通常p为小于或等于表长(最好接近m)的最小质数或不包含小于20质因子的合数。
关键在于p值的确定。
6.随机数法
取关键字的随机函数值作为它的散列地址。f(key) = random(key).
特点是适合关键字长度不等时。
3)散列冲突的解决办法
答:散列冲突是对于不同的关键字,他们计算得到的散列地址是相同的。如何解决呢?
1.开放定址法(重点)
开放定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。
2.再散列函数法
3.链地址法(重点)
4.公共溢出区法
4)散列表查找实现
答:基于数组实现哈希表
主要包括定义哈希表底层数据结构(数组:静态或者动态),初始化哈希表,哈希函数的设计,插入操作的实现(需要解决冲突),查找操作的实现(需要解决冲突),重建哈希表等。
1.构建散列表数据结构
答:
class HashTable //此哈希表中的关键字是字符串,不是单个字符(字符串本身需要数组来存储)
{
public:
private:
int size; //定义散列表长度:
char ** elem; //动态数组的首地址,即散列表的首地址 (可以用静态数组实现:定义一个指针数组)
//定义**elem,表示elem是一个“指向指针”的指针,而定义*elem,表示elem是一个“指向char型”的指针(如果我们的关键字是单个字符,这里用*elem)
//elem是动态分配数组的首地址,该数组中每个元素都是一个指针,指向一个char型数组
};
2.定义哈希函数
答:
int HashTable::hash(char value[]) //构造哈希函数:返回值是关键字value[]对应的散列地址
{
int f_key = 0; //散列地址
//根据关键字的长度、每位数值来生成散列地址
for (int i = 0; i < strlen(value); i++) //strlen()是求出char数组value的长度,即字符串长度
{
f_key = (f_key * 256 + 128 + value[i]) % size; //求出每个字符串在数组中的索引位置(散列表地址)
}
return f_key;
}
2.散列表的初始化
答:
HashTable::HashTable() //初始化哈希表:申请连续存储空间作为散列表
{
size = Maxsize;
elem = new char* [size]; //程序运行时,开始分配内存空间
//在堆区开辟一个大小为size的数组,数组里面的数据类型为char*,即每个数据元素是一个指向char型的指针。返回这个存放“指向char型的指针”数组的首地址
//如果每个数据元素是数字或者单个字符,即 elem = new int [size]; 或elem = new char [size];
for (int i = 0; i < size; i++)
{
elem[i] = NULL; //“指向char型的指针”的数组,每个数据元素都为NULL。
//将来每个elem[i]存储的是某个字符数组的首地址,不过此时由于不知道每个插入字符数组的大小,还没有为其分配内存空间。
}
}
3.散列表的插入操作
答:
思路:
先判断散列表中是否已经有待插入的值,否则,根据哈希函数计算散列地址。
然后判断是否发生冲突,当解决冲突时,插入该值。
(增加功能:若直到散列表最后一个位置都无法解决冲突,就重建哈希表)
bool HashTable::insert(char value[]) //插入函数
{
int pos = 0;
int times = 0;
if (search(value,pos,times))
{
return false; //散列表中已存在待插入的值
}
else //散列表中无该元素,重置pos和times,准备插入元素
{
pos = 0;
times = 0;
}
pos = hash(value); //计算哈希地址
while (elem[pos] != NULL && times < size - pos) //当待存储位置不为空,说明发生了冲突,需要根据线性探测法找下一个位置
{
times++;
pos = (pos + 1) % size;
}
if (elem[pos] == NULL) //找到空闲位置
{
elem[pos] = new char[strlen(value) + 1]; // 由于插入的值是字符串,因此需要根据字符串的长度,创建字符串存储空间,返回字符串的首地址。
elem[pos] = value; //由于value是字符串,这里使用value不是获取地址,而是表示整个字符串(不同于整型数组),因此这里相等于两个字符数组之间的赋值。
return true;
}
else //散列表空间不够,无法解决冲突,需要重建
{
return false;//重建哈希表,并插入成功
}
}
4.散列表的查找实现
答:
思路:
首先,根据哈希函数,得到初步索引位置(散列地址)
其次判断是否发生冲突,如果发生并解决,直到找到最终索引位置
bool HashTable::search(char value[], int &pos, int ×)//查找函数:value[]是被查找的值,pos是最终对应的散列表地址(索引位置),times是冲突次数
{
pos = hash(value); //1.根据哈希函数,得到初步索引位置(散列地址)
//2.判断是否发生冲突,如果发生并解决
times = 0;
while(elem[pos] != NULL && strcmp(elem[pos], value) != 0) //elem[pos]表示某个字符串:当初始散列地址存储的数据不为空,且该数据不与关键字相等,说明发生了冲突。如果elem[pos] != NULL,说明不存在要查找的值,因为其没有初始索引位置
{
times++; //冲突次数加1(times最多为散列表长度)
if (times < size)
{
pos = (pos + 1) % size; //开放定址法中的线性探测法解决冲突,每执行一次,索引位置pos加1
}
else //遍历了散列表数组中的所有索引位置
{
return 0;
}
}
if (elem[pos] != NULL && strcmp(elem[pos], value) == 0) //查找到value
{
return 1; //pos是value在散列表中的索引位置(散列表地址)
}
else //如果elem[pos] != NULL,说明不存在要查找的值,因为其没有初始索引位置
{
return 0;
}
}
5.释放哈希表
答:
思路:手动删除向内存申请的空间
HashTable::~HashTable()
{
for (int i = 0; i < size; i++)
{
if (elem[i] != NULL)
{
delete[] elem[i]; //先删除每个字符数组
}
}
delete[] elem; //最后删除“指向字符数组的指针”的数组
}
5)散列表性能分析
答:
理想查找时间复杂度为O(1)。当发生冲突时,查找性能降低。
散列查找的平均查找长度取决于哪些因素呢?
散列函数是否均匀、处理冲突的方法 、装填因子
6)哈希表的进阶
答:
数组作为哈希表,set容器作为哈希表,map容器作为哈希表
数组作为哈希表:能够确定数组大小,当数组空间够大,但哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。
set容器作为哈希表:unordered_set是一个集合,里面放的元素只能是一个key。但是没有下标。
map容器作为哈希表:map是一种
注:map确实可以解决数组和set的问题,但使用map的空间消耗要比数组、set大一些。所以原则问题是,简单用数组,复杂用set和map.