C++ 字典树详解(含例题)

C++ 字典树详解(含例题)

字典树(trie)的定义

顾名思义，就是一个像字典一样的树，谢谢观看
我们想要熟练的运用字典树，首先肯定要知道什么样的结构才会被称之为字典树吧。

字典树是一种树形结构，典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较———百度百科

从上面的百度百科的一段定义中，我们知道了字典树是：利用字符串的公共前缀来减少复杂度；用于统计，排序和保存大量字符串的数据结构
--------------------------一道并不华丽的分割线-----------------------------
那么我们来康一康字典树究竟长什么样子：

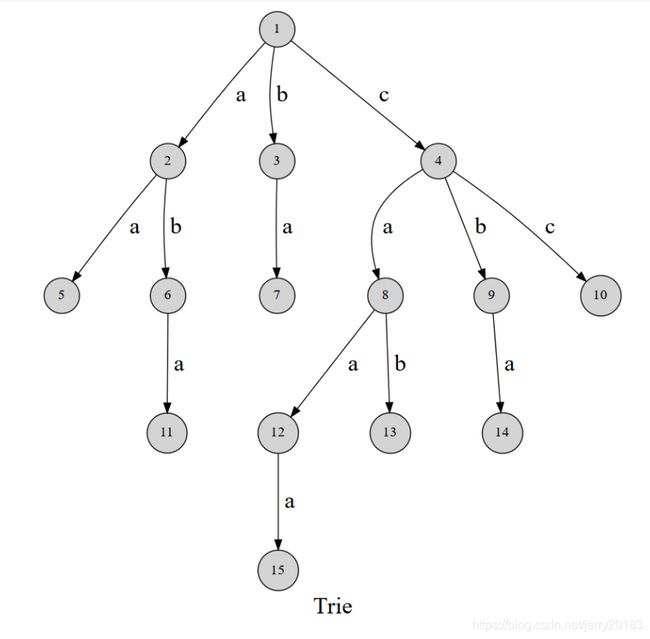
可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子：1->2->6->11就是aba
如果我们只看上面的图，我们其实是可以看到一个问题的：
如果我们还有一个字符串名为caa(1->4->8->12)，图上却又有一个字符串名为caaa(1->4->8->12->15)，那么我们该如何判断字符串caa存在呢？ 听起来有点绕，是吧？
简而言之其实就是： 字典树中如何判断一个字符串的前缀是否存在？
答案就是：多加一个bool数组，如果是一个字符串的结尾就将其标为true(多简单啊)

字典树的构造

知道了字典树是个什么东西之后我们就可以尝试一下亲手构造一棵字典树，构造字典树当然有两种方法来构造，请看下文
下面的代码是一个字典树的模板

int nex[100005][26],cnt;
bool exist[100005];//该结点结尾的字符串是否存在
void insert(char *s, int l) {  // 插入字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) nex[p][c] = ++cnt;  // 如果没有，就添加结点
      p = nex[p][c];
    }
    exist[p] = 1;
  }
bool find(char *s, int l) {  //查找字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      	int c = s[i] - 'a';
      	if (!nex[p][c]) return 0;
      	p = nex[p][c];
    }
    return exist[p];
}

我相信有人会跟我一样第一次看不懂nex[]和exist[]是怎么共同构造出一个字典树的。

代码解析

我们用 nxt[u][v] 表示结点 u 的 c 字符指向的下一个结点，或着说是结点 代表的字符串后面添加一个字符 c 形成的字符串的结点。( c 的取值范围和字符集大小有关，不一定是 0~26 。)

有时需要标记插入进 trie 的是哪些字符串，每次插入完成时在这个字符串所代表的节点处打上标记即可。

线段树的应用

检索字符串

字典树的最基础的运用当然就是检索字符串啦~来道题目康康
于是他错误的点名开始了

朴素算法

看完这道题目就会很容易的想出一种朴素的算法，就是每次点一个名就去名单里面暴力查找，如果有而且只点了一次名就输出"OK", 重复就输出"REPEAT"，如果找都没找到就输出"WRONG"，然后就会，就会。。。

气不气？气不气？T了两个点就是不让过，那么哪里不行呢？我们可以分析一下数据范围，n≤10⁴，m≤10⁵，朴素算法至少是O(nm)，即10⁹，绝对超标。

字典树

这一道题目，其实可以算是一道字典树的裸题，大量的查找以及很短的字符串长度，是可以很轻易的想出字典树的解法的。
方法其实就是对每一个名单上的名字建立字典树，然后对于每一个报出的名字去查找，然后加一个int数组对每一个名字计数判断是不是第一次点到这个名字就OK啦~
上代码上代码：

#include 
const int N = 500010;
char s[60];
int n, m, ch[N][26], tag[N], tot = 1;
int main() {
  scanf("%d", &n);
  for (int i = 1; i <= n; ++i) {
    scanf("%s", s + 1);
    int u = 1;
    for (int j = 1; s[j]; ++j) {
      int c = s[j] - 'a';
      if (!ch[u][c]) ch[u][c] = ++tot;
      u = ch[u][c];
    }
    tag[u] = 1;
  }
  scanf("%d", &m);
  while (m--) {
    scanf("%s", s + 1);
    int u = 1;
    for (int j = 1; s[j]; ++j) {
      int c = s[j] - 'a';
      u = ch[u][c];
      if (!u) break;  // 不存在对应字符的出边说明名字不存在
    }
    if (tag[u] == 1) {
      tag[u] = 2;
      puts("OK");
    } else if (tag[u] == 2)
      puts("REPEAT");
    else
      puts("WRONG");
  }
  return 0;
}

维护异或和

其实字典树可绝对不止检索字符串这点能力，字典树的另外一个能力就是维护异或和

字典树支持修改（删除 + 重新插入），和全局加一（即：让其所维护所有数值递增 1 ，本质上是一种特殊的修改操作）。

如果要维护异或和，需要按值从低位到高位建立 trie。

一个约定 ：文中说当前节点 往上 指当前节点到根这条路径，当前节点 往下 指当前结点的子树。

插入 & 删除

如果要维护异或和，我们 只需要 知道某一位上 0 和 1 个数的奇偶性即可，也就是对于数字 1 来说，当且仅当这一位上数字 1 的个数为奇数时，这一位上的数字才是 1 ，请时刻记住这段文字：如果只是维护异或和，我们只需要知道某一位上 1 的数量即可，而不需要知道 trie 到底维护了哪些数字。

说了这么多，我们来看一道例题吧~
P6018 题目传送门

思路

每个结点建立一棵 trie 维护其儿子的权值，trie 应该支持全局加一。 可以使用在每一个结点上设置懒标记来标记儿子的权值的增加量。

代码

#include
using namespace std;
const int _ = 5e5 + 10;
namespace trie {
const int _n = _ * 25;
int rt[_];
int ch[_n][2];
int w[_n];  //`w[o]` 指节点 `o` 到其父亲节点这条边上数值的数量（权值）。
int xorv[_n];
int tot = 0;
void maintain(int o) {
  w[o] = xorv[o] = 0;
  if (ch[o][0]) {
    w[o] += w[ch[o][0]];
    xorv[o] ^= xorv[ch[o][0]] << 1;
  }
  if (ch[o][1]) {
    w[o] += w[ch[o][1]];
    xorv[o] ^= (xorv[ch[o][1]] << 1) | (w[ch[o][1]] & 1);
  }
}
inline int mknode() {
  ++tot;
  ch[tot][0] = ch[tot][1] = 0;
  w[tot] = 0;
  return tot;
}
void insert(int &o, int x, int dp) {
  if (!o) o = mknode();
  if (dp > 20) return (void)(w[o]++);
  insert(ch[o][x & 1], x >> 1, dp + 1);
  maintain(o);
}
void erase(int o, int x, int dp) {
  if (dp > 20) return (void)(w[o]--);
  erase(ch[o][x & 1], x >> 1, dp + 1);
  maintain(o);
}
void addall(int o) {
  swap(ch[o][1], ch[o][0]);
  if (ch[o][0]) addall(ch[o][0]);
  maintain(o);
}
}  // namespace trie

int head[_];
struct edges {
  int node;
  int nxt;
} edge[_ << 1];
int tot = 0;
void add(int u, int v) {
  edge[++tot].nxt = head[u];
  head[u] = tot;
  edge[tot].node = v;
}

int n, m;
int rt;
int lztar[_];
int fa[_];
void dfs0(int o, int f) {
  fa[o] = f;
  for (int i = head[o]; i; i = edge[i].nxt) {
    int node = edge[i].node;
    if (node == f) continue;
    dfs0(node, o);
  }
}
int V[_];
inline int get(int x) { return (fa[x] == -1 ? 0 : lztar[fa[x]]) + V[x]; }
int main() {
  cin>>n>>m;
  for (int i = 1; i < n; i++) {
    int u, v;
    cin>>u>>v;
    add(u, v);
    add(rt = v, u);
  }
  dfs0(rt, -1);
  for (int i = 1; i <= n; i++) {
    cin>>V[i];
    if (fa[i] != -1) trie::insert(trie::rt[fa[i]], V[i], 0);
  }
  while (m--) {
    int opt, x;
    cin>>opt>>x;
    if (opt == 1) {
      lztar[x]++;
      if (x != rt) {
        if (fa[fa[x]] != -1) trie::erase(trie::rt[fa[fa[x]]], get(fa[x]), 0);
        V[fa[x]]++;
        if (fa[fa[x]] != -1) trie::insert(trie::rt[fa[fa[x]]], get(fa[x]), 0);
      }
      trie::addall(trie::rt[x]);
    } else if (opt == 2) {
      int v;
      cin>>v;
      if (x != rt) trie::erase(trie::rt[fa[x]], get(x), 0);
      V[x] -= v;
      if (x != rt) trie::insert(trie::rt[fa[x]], get(x), 0);
    } else {
      int res = 0;
      res = trie::xorv[trie::rt[x]];
      res ^= get(fa[x]);
      printf("%d\n", res);
    }
  }
  return 0;
}

本篇有关于字典树的博客到这里就结束了，感谢观看:-)