树状数组与线段树
文章目录
- 一.树状数组
-
-
- 核心函数
-
- 二.线段树
-
-
-
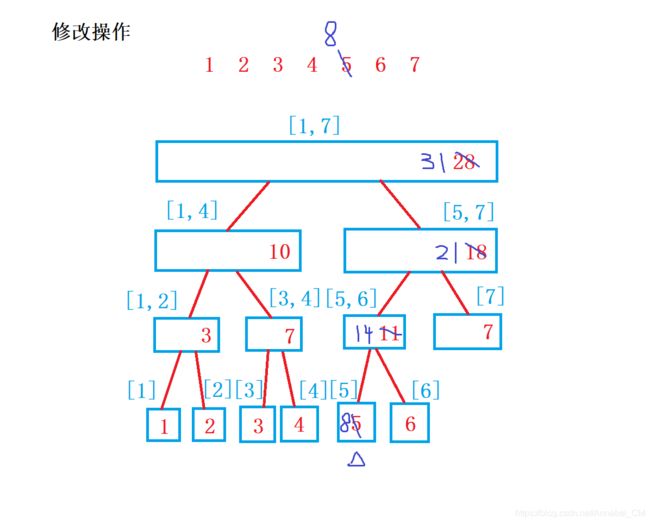
- 修改操作
- 查询操作
-
- 1.动态求连续区间和
-
-
- 树状数组
- 线段树
-
- 2.数星星
- 3.数列区间最大值
- 4.小朋友排队
- 5.油漆面积
- 6.三体攻击
- 7.螺旋折线
-
一.树状数组
- 给区间的某个位置上的数加上一个数(单点修改)
- 快速动态地求某一个前缀和(区间查询)
原数组A 数组底数从1开始
树状数组C:i为奇数 C[i] = A[i]
i为偶数 C[i] = A[1] +…+A[i]

lowbit(x) = x& -x;
c[x] = (x - lowbit(x), x);
-
1、lowbit(x):返回x的最后一位1
-
2、add(x,v):在x位置加上v,并将后面相关联的位置也加上v
-
3、query(x):询问x的前缀和
核心函数
int lowbit(int x)
{
return x & -x;
}
void add(int x, int y)//更新
{
for(int i = x; i <= n; i += lowbit(i)) tr[i] += y;
}
int query(int x)//求和
{
int res = 0;
for(int i = x; i; i -= lowbit(i)) res +=tr[i];
return res;
}
二.线段树
线段树,英文名称是Segment Tree,其本质也是一个二叉搜索树,区别在于线段树的每一个节点记录的都是一个区间,每个区间都被平均分为2个子区间,作为它的左右儿子。比如说区间[1,10],被分为区间[1,5]作为左儿子,区间[6,10]作为右儿子:
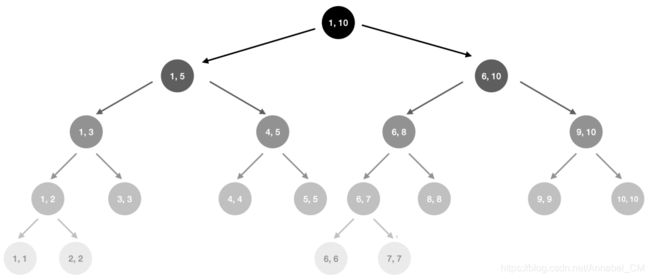
操作1:单点修改(递归+回溯)
操作2:区间查询(某个区间的总和)
pushup:用子节点信息更新当前信息
build:在一段区间上初始化
modify:修改
query:查询
- 1、pushup(u):用子节点信息来更新当前节点信息(把信息往上传递)
- 2、build(u,l,r):在一段区间上初始化线段树,其中u表示根结点,l表示左边界,r表示右边界
- 3、query(u,l,r):查询某段区间的和,其中u表示根结点,l表示左边界,r表示右边界
- 4、modify(u,x,v):修改操作,在u结点中,x位置加上v
修改操作
查询操作
1.动态求连续区间和
ACWing1264. 动态求连续区间和
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。
数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。
数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35
树状数组
#include线段树
#include 2.数星星
ACWing1265. 数星星
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。
如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。
例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。
例图中有 1 个 0 级,2 个 1 级,1 个 2 级,1 个 3 级的星星。
给定星星的位置,输出各级星星的数目。
换句话说,给定 N 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
输入格式
第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y 表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
输出格式
N 行,每行一个整数,分别是 0 级,1 级,2 级,……,N−1 级的星星的数目。
数据范围
1≤N≤15000,
0≤x,y≤32000
输入样例:
5
1 1
5 1
7 1
3 3
5 5
输出样例:
1
2
1
1
0
#include3.数列区间最大值
ACWing1270. 数列区间最大值
输入一串数字,给你 M 个询问,每次询问就给你两个数字 X,Y,要求你说出 X 到 Y 这段区间内的最大数。
输入格式
第一行两个整数 N,M 表示数字的个数和要询问的次数;
接下来一行为 N 个数;
接下来 M 行,每行都有两个整数 X,Y。
输出格式
输出共 M 行,每行输出一个数。
数据范围
1≤N≤105,
1≤M≤106,
1≤X≤Y≤N,
数列中的数字均不超过231−1
输入样例:
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8
输出样例:
5
8
#include 4.小朋友排队
AcWing1215. 小朋友排队
n 个小朋友站成一排。
现在要把他们按身高从低到高的顺序排列,但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。
开始的时候,所有小朋友的不高兴程度都是 0。
如果某个小朋友第一次被要求交换,则他的不高兴程度增加 1,如果第二次要求他交换,则他的不高兴程度增加 2(即不高兴程度为 3),依次类推。当要求某个小朋友第 k 次交换时,他的不高兴程度增加 k。
请问,要让所有小朋友按从低到高排队,他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样,则他们谁站在谁前面是没有关系的。
输入格式
输入的第一行包含一个整数 n,表示小朋友的个数。
第二行包含 n 个整数 H1,H2,…,Hn,分别表示每个小朋友的身高。
输出格式
输出一行,包含一个整数,表示小朋友的不高兴程度和的最小值。
数据范围
1≤n≤100000,
0≤Hi≤1000000
输入样例:
3
3 2 1
输出样例:
9
样例解释
首先交换身高为3和2的小朋友,再交换身高为3和1的小朋友,再交换身高为2和1的小朋友,每个小朋友的不高兴程度都是3,总和为9。
冒泡排序 时间太久,可以考虑归并排序和线段树的方法,记录每个数前面比它大的数的个数,以及后面比它小是数的个数,就是他们应该要交换的最小数,需要考虑分配问题,平均分配,不高兴程度比较小。
贪心的想法:每个数的交换次数是固定的;记录每个数前面比它大的数的个数,以及后面比它小是数的个数,就是他们应该要交换的最小数。
#include5.油漆面积
AcWing1228. 油漆面积
X星球的一批考古机器人正在一片废墟上考古。
该区域的地面坚硬如石、平整如镜。
管理人员为方便,建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。
它们感兴趣的内容也不相同。
经过各种测量,每个机器人都会报告一个或多个矩形区域,作为优先考古的区域。
矩形的表示格式为 (x1,y1,x2,y2),代表矩形的两个对角点坐标。
为了醒目,总部要求对所有机器人选中的矩形区域涂黄色油漆。
小明并不需要当油漆工,只是他需要计算一下,一共要耗费多少油漆。
其实这也不难,只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意,各个矩形间可能重叠。
输入格式
第一行,一个整数 n,表示有多少个矩形。
接下来的 n 行,每行有 4 个整数 x1,y1,x2,y2,空格分开,表示矩形的两个对角顶点坐标。
输出格式
一行一个整数,表示矩形覆盖的总面积。
数据范围 输入样例1: 输出样例1: 输入样例2: 输出样例2: 输入样例: 输出样例: 样例解释 ACWing1237. 螺旋折线
1≤n≤10000,
0≤x1,x2,y2,y2≤10000
数据保证 x13
1 5 10 10
3 1 20 20
2 7 15 17
340
3
5 2 10 6
2 7 12 10
8 1 15 15
128
#include 6.三体攻击
2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2
2
在第 2 轮攻击后,战舰 (1,1,1) 总共受到了 2 点伤害,超出其防御力导致爆炸。#include 7.螺旋折线
如下图所示的螺旋折线经过平面上所有整点恰好一次。

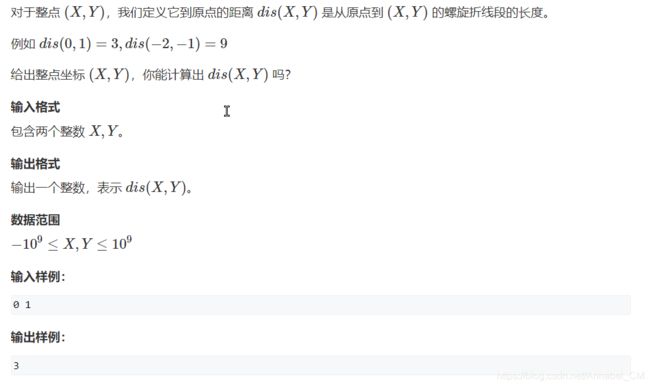

找规律,先找每个对角线上的规律,然后找每条边的规律,找到偏移量如何计算
(x, y)—> 先判断是在哪个方向上的边—> 找该方向的特殊点(起点)#include