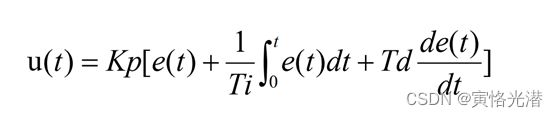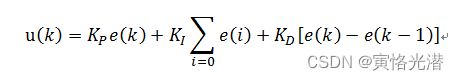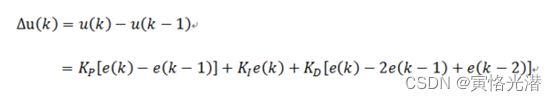Jetbotmini中的PID驱动算法控制与代码实现

PID算法在工业领域应用极为广泛，汽车、飞机、导弹、设备上的温度控制等等都有它的身影，其中的PID三个字母分别是Proportional比例、Integral积分、Derivative微分的首字母，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法。PID控制的实质就是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出，通过这三个算法的组合可有效地纠正被控制对象的偏差，从而使其达到一个稳定的状态。

更多详情可以查看百度百科的解释：PID算法

举个简单通俗的例子，比如说自动驾驶，保持30码的速度，如果说按照常见的思维，低于30码就踩油门加速，高于30码就踩刹车减速，那车子就会很不稳定了，时快时慢，坐起来不舒服之外，安全也是个问题，所以这个时候就用到PID控制了，就是说，低于30码没多少的情况，我就轻轻加点油，高于30码就轻轻带点刹车，这样车子显得很平稳。当然这个例子看起来只说明了P这个按比例的调节，显然也是不会有很好的效果，还需要用到微分和积分，意思就是让它们微调，这样可以做到一个很好的稳定输出。

1、PID公式与说明

我们先来熟悉下PID的公式，如下：

Kp：比例增益，Kp与比例度成倒数关系

Tt：积分时间常数

TD：微分时间常数

u(t)：PID控制器的输出信号

e(t)：给定值r(t)与测量值之差，或说两次误差的差值

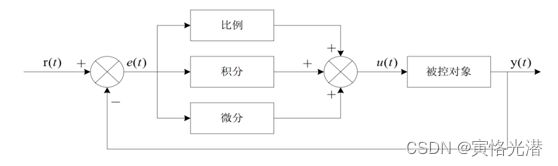
PID控制器如图：

图中可以看到经过三个算法的相加，得到一个稳定的输出，然后应用到被控制的对象。

PID三个算法(也可以看成是调三个参数)的说明如下：

比例(Proportional)：在模拟 PID 控制器中，比例环节的作用是对偏差瞬间作出反应。偏差一旦产生，控制器就立即产生控制作用，使控制量向减少偏差的方向变化。控制作用的强弱取决于比例系数 ，比例系数越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；但是越大，也越容易产生振荡，破坏系统的稳定性。故而，比例系数的选择必须恰当，才能过渡时间少，静差小而又稳定的效果

积分(Integral)：从积分部分的数学表达式可以知道，只要存在偏差，则它的控制作用就不断的增加；只有在偏差时，它的积分才能是一个常数，控制作用才是一个不会增加的常数。可见，积分部分可以消除系统的偏差。e(t)＝0积分环节的调节作用虽然会消除静态误差，但也会降低系统的响应速度，增加系统的超调量。积分常数越大，积分的积累作用越弱，这时系统在过渡时不会产生振荡；但是增大积分常数会减慢静态误差的消除过程，消除偏差所需的时间也较长，但可以减少超调量，提高系统的稳定性。当Ti 较小时，则积分的作用较强，这时系统过渡时间中有可能产生振荡，不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定Ti。

微分(Derivative)：实际的控制系统除了希望消除静态误差外，还要求加快调节过程。在偏差出现的瞬间，或在偏差变化的瞬间，不但要对偏差量做出立即响应（比例环节的作用），而且要根据偏差的变化趋势预先给出适当的纠正。为了实现这一作用，可在PI控制器的基础上加入微分环节，形成PID控制器。微分环节的作用是阻止偏差的变化。它是根据偏差的变化趋势（变化速度）进行控制。偏差变化的越快，微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入，将有助于减小超调量，克服振荡，使系统趋于稳定，特别对高阶系统非常有利，它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分，或在微分起作用之前先对输入信号进行滤波。微分部分的作用由微分时间常数Td决定。Td越大时，则它抑制偏差变化的作用越强；Td越小时，则它反抗偏差变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分常数Td，可以使微分作用达到最优。

数字式 PID 控制算法可以分为位置式PID和增量式PID控制算法。那么我们在决定选择使用哪个PID算法之前我们应该先要了解它们各自的原理：

2、位置式PID算法

e(k): 用户设定的值（目标值）- 控制对象的当前的状态值

比例Kp：e(k)

积分：∑e(i)，误差的累加

微分：e(k) - e(k-1)，这次误差-上次误差

位置式PID的含义就是当前系统的实际位置，与你想要达到的预期位置的偏差，进行PID控制。

因为有误差积分∑e(i)的一直累加，也就是当前的输出u(k)与过去的所有状态都有关系，用到了误差的累加值；输出的u(k)对应的是执行机构的实际位置，一旦控制输出出错(控制对象的当前状态值出现问题 )，u(k)的大幅变化会引起系统的大幅变化并且位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积，一旦误差开始反向变化，系统需要一定时间从饱和区退出，所以在u(k)达到最大和最小时，要停止积分作用，并且要有积分限幅和输出限幅，所以在使用位置式PID时，一般我们直接使用PD控制，而位置式 PID 适用于执行机构不带积分部件的对象，如舵机，平衡小车的直立和温控系统的控制

3、增量式PID算法

比例KP：e(k)-e(k-1)，这次误差-上次误差

积分KI：e(i)，误差

微分KD：e(k) - 2e(k-1)+e(k-2)，这次误差-2*上次误差+上上次误差

增量式PID根据公式可以很好地看出，只要使用前后三次测量值的偏差，即可由公式求出控制增量而得出的控制量▲u(k)对应的是近几次位置误差的增量，而不是对应与实际位置的偏差，没有误差累加，也就是说，增量式PID中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果，并且在系统发生问题时，增量式不会严重影响系统的工作

4、位置式PID与增量式PID的区别和优缺点

4.1、两者区别

1、增量式算法不需要做累加，控制增量的确定仅与最近几次偏差采样值有关，计算误差对控制量计算的影响较小。而位置式算法要用到过去偏差的累加值，容易产生较大的累加误差。

2.、增量式算法得出的是控制量的增量，例如在阀门控制中，只输出阀门开度的变化部分，误差动作影响小，必要时还可通过逻辑判断限制或禁止本次输出，不会严重影响系统的工作。而位置式的输出直接对应对象的输出，因此对系统影响较大。

3.、增量式PID控制输出的是控制量增量，并无积分作用，因此该方法适用于执行机构带积分部件的对象，如步进电机等。而位置式PID适用于执行机构不带积分部件的对象，如电液伺服阀。

4、在进行PID控制时，位置式PID需要有积分限幅和输出限幅，而增量式PID只需输出限幅

4.2、位置式PID优缺点

优点：

①位置式PID是一种非递推式算法，可直接控制执行机构（如平衡小车），u(k)的值和执行机构的实际位置（如小车当前角度）是一一对应的，因此在执行机构不带积分部件的对象中可以很好的应用。

缺点：

①每次输出均与过去的状态有关，计算时要对e(k)进行累加，运算工作量大。

4.3、增量式PID优缺点

优点：

①误动作时影响小，必要时可使用逻辑判断的方法去掉出错数据。

②手动/自动切换时冲击小，便于实现无扰动切换。当计算机故障时，仍能保持原值。

③算式中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关。

缺点：

①积分截断效应大，有稳态误差。

②溢出的影响大，有的被控对象用增量式则不太好。

下面我们通过代码并可视化，大家可能就更清楚这个算法的妙处了，代码是通过ChatGPT4的生成，然后增加可视化的代码，让大家直观感受下。

5、位置式PID代码

import numpy as np
import matplotlib.pyplot as plt

class PID:
  def __init__(self, Kp, Ki, Kd):
    self.Kp = Kp # 比例系数
    self.Ki = Ki # 积分系数
    self.Kd = Kd #微分系数
    self.last_error = 0 # 上一次的误差
    self.integral = 0 # 误差积分值
    
  def update(self, setpoint, position, dt):
    '''setpoint:目标值、position:当前位置、dt:时间步长'''
    self.setpoint = setpoint
    self.position = position
    self.dt = dt
    error = self.setpoint - self.position # 当前误差
    self.integral += error * dt # 积分项
    derivative = (error - self.last_error) / dt #微分项
    output = self.Kp * error + self.Ki * self.integral + self.Kd * derivative
    self.last_error = error
    self.position = output
    return self.position

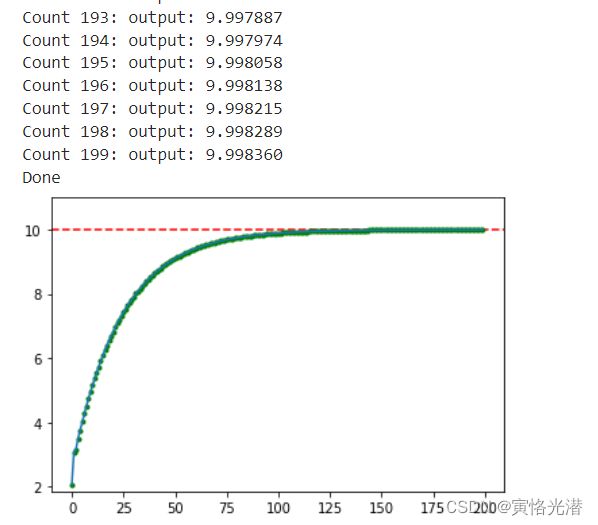
  def fit_and_plot(self, count = 100):
    counts = np.arange(count)
    outputs = []
    for i in counts:
      outputs.append(self.update(self.setpoint,self.position,self.dt))
      print('Count %3d: output: %f' % (i, outputs[-1]))
    print('Done')
        
    plt.figure()
    plt.axhline(self.setpoint, c='red',ls='--')
    plt.plot(counts, np.array(outputs), 'g.')
    plt.ylim(min(outputs) - 0.1 * min(outputs), max(outputs) + 0.1 * max(outputs))
    plt.plot(outputs)
    plt.show()


pid = PID(0.2, 0.1, 0.01)
setpoint = 10.0
position = -5.0
dt = 0.5
pid.update(setpoint, position, dt)
pid.fit_and_plot(200)

6、增量式PID代码

import numpy as np
import matplotlib.pyplot as plt

class PID(object):
    def __init__(self, setpoint, position, dt, Kp, Ki, Kd) -> None:
        self.dt = dt  # 时间步长
        self.Kp = Kp  # 比例系数
        self.Ki = Ki  # 积分系数
        self.Kd = Kd  # 微分系数

        self.setpoint = setpoint
        self.position = position
        self._pre_error = 0  # t-1 时刻误差值
        self._pre_pre_error = 0  # t-2 时刻误差值

    def update(self):
        error = self.setpoint - self.position
        p_change = self.Kp * (error - self._pre_error)
        i_change = self.Ki * error
        d_change = self.Kd * (error - 2 * self._pre_error + self._pre_pre_error)
        delta_output = p_change + i_change + d_change  # 本次增量
        self.position += delta_output  # 计算当前位置

        self._pre_pre_error = self._pre_error
        self._pre_error = error

        return self.position

    def fit_and_plot(self, count=100):
        counts = np.arange(count)
        outputs=[]
        for i in counts:
            outputs.append(self.update())
            print('Count %3d: output: %f' % (i, outputs[-1]))
        print('Done')

        plt.figure()
        plt.axhline(self.setpoint, c='red',ls='-.',lw=2)  # 水平线，其中垂直线就是axvline
        plt.plot(counts, np.array(outputs), 'g.')
        plt.ylim(min(outputs) - 0.1 * min(outputs),max(outputs) + 0.1 * max(outputs))
        plt.plot(outputs)
        plt.show()

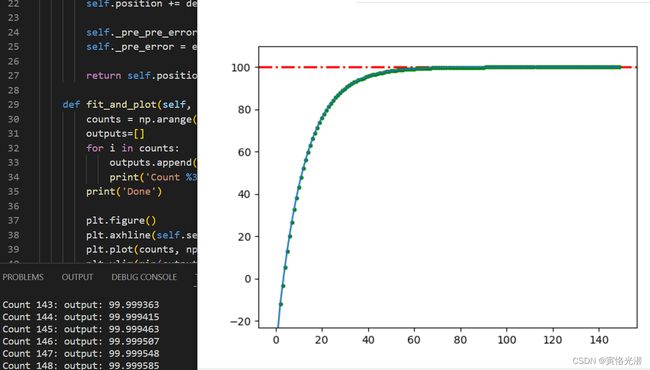
pid = PID(100, -80, 0.5, 0.2, 0.1, 0.001)
pid.fit_and_plot(150)

7、无人车中使用PID驱动

我们来看下无人车里面的驱动文件是怎么写的，PID.py源码如下：

'''
@Copyright (C): 2010-2019, Shenzhen Yahboom Tech
@Author: Malloy.Yuan
@Date: 2019-07-30 20:34:09
@LastEditors: Malloy.Yuan
@LastEditTime: 2019-08-08 16:10:46
'''
#  PID控制一阶惯性系统测试程序
#  PPID control first-order inertial system test program
#*****************************************************************#
#                      增量式PID系统                              #
#                 Incremental PID system                          #
#*****************************************************************#
class IncrementalPID:
    def __init__(self, P, I, D):
        self.Kp = P
        self.Ki = I
        self.Kd = D
 
        self.PIDOutput = 0.0             #PID控制器输出
                                         #PID controller output
        self.SystemOutput = 0.0          #系统输出值
                                         #System output value
        self.LastSystemOutput = 0.0      #上次系统输出值
                                         #Last system output value
        self.Error = 0.0                 #输出值与输入值的偏差
                                         #Deviation between output value and input value
        self.LastError = 0.0
        self.LastLastError = 0.0
 
    #设置PID控制器参数
    #Set PID controller parameters
    def SetStepSignal(self,StepSignal):
        self.Error = StepSignal - self.SystemOutput
        IncrementValue = self.Kp * (self.Error - self.LastError) +\
        self.Ki * self.Error +\
        self.Kd * (self.Error - 2 * self.LastError + self.LastLastError)

        self.PIDOutput += IncrementValue
        self.LastLastError = self.LastError
        self.LastError = self.Error

    #设置一阶惯性环节系统  其中InertiaTime为惯性时间常数
    #Set the first-order inertial link system, where inertiatime is the inertial time constant
    def SetInertiaTime(self,InertiaTime,SampleTime):
        self.SystemOutput = (InertiaTime * self.LastSystemOutput + \
            SampleTime * self.PIDOutput) / (SampleTime + InertiaTime)

        self.LastSystemOutput = self.SystemOutput
 
 
# *****************************************************************#
#                      位置式PID系统                               #
#                   Position PID system                            #
# *****************************************************************#
class PositionalPID:
    def __init__(self, P, I, D):
        self.Kp = P
        self.Ki = I
        self.Kd = D
 
        self.SystemOutput = 0.0
        self.ResultValueBack = 0.0
        self.PidOutput = 0.0
        self.PIDErrADD = 0.0
        self.ErrBack = 0.0
    
    #设置PID控制器参数
    #Set PID controller parameters
    def SetStepSignal(self,StepSignal):
        Err = StepSignal - self.SystemOutput
        KpWork = self.Kp * Err
        KiWork = self.Ki * self.PIDErrADD
        KdWork = self.Kd * (Err - self.ErrBack)
        self.PidOutput = KpWork + KiWork + KdWork
        self.PIDErrADD += Err
        self.ErrBack = Err

    #设置一阶惯性环节系统  其中InertiaTime为惯性时间常数
    #Set the first-order inertial link system, where inertiatime is the inertial time constant
    def SetInertiaTime(self, InertiaTime,SampleTime):
       self.SystemOutput = (InertiaTime * self.ResultValueBack + \
           SampleTime * self.PidOutput) / (SampleTime + InertiaTime)
       self.ResultValueBack = self.SystemOutput

#导入模块PID.py
import PID
#创建控制实例
follow_speed_pid = PID.PositionalPID(1.5, 0, 0.05)
turn_gain_pid = PID.PositionalPID(0.15, 0, 0.05)

然后对PID控制器配置出口(original value + xservo_pid.SystemOutput)、入口值(Now_value)，设置惯性常数(InertiaTime)，采样时间常数(SampleTime)，初始值(original_value)。

惯性时间常数(InertiaTime)：简单来说就是克服惯性所需要花费的时间。

采样时间常数(SampleTime)：表示PID控制器上一次输入数据与邻近一次输入数据的间隔时间，大致等于进入PID控制器的主函数的循环一次所花费的时间。

follow_speed_pid.SystemOutput = Now_value
follow_speed_pid.SetStepSignal(Target_value)
follow_speed_pid.SetInertiaTime(InertiaTime, SampleTime)
target_valuex = int(original_value + follow_speed_pid.SystemOutput)

通过上面的步骤，基本的PID控制器就完成了

8、PID控制器调参

这个跟前面深度学习中的超参数等类似，要想得到一组合适的参数也需要进行调试，在PID中调参非常烦杂，下面是一些经验调参步骤：

1、确定比例系数Kp

确定比例系数Kp时，首先去掉PID的积分项和微分项，可以令Ti=0、Td=0，使之成为纯比例调节。输入设定为系统允许输出最大值的60％～70％，比例系数Kp由0开始逐渐增大，直至系统出现振荡；再反过来，从此时的比例系数Kp逐渐减小，直至系统振荡消失。记录此时的比例系数Kp，设定PID的比例系数Kp为当前值的60％～70％。

2、确定积分时间常数Ti

比例系数Kp确定之后，设定一个较大的积分时间常数Ti，然后逐渐减小Ti，直至系统出现振荡，然后再反过来，逐渐增大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150％～180％。

3、确定微分时间常数Td

微分时间常数Td一般不用设定，为0即可，此时PID调节转换为PI调节。如果需要设定，则与确定Kp的方法相同，取不振荡时其值的30％。

4、系统空载、带载联调

对PID参数进行微调，直到满足性能要求。

网上流传着调试PID的口诀，如下：

参数整定找最佳， 从小到大顺序查。
先是比例后积分， 最后再把微分加。
曲线振荡很频繁， 比例度盘要放大。
曲线漂浮绕大弯， 比例度盘往小扳。
曲线偏离回复慢， 积分时间往下降。
曲线波动周期长， 积分时间再加长。
曲线振荡频率快， 先把微分降下来。
动差大来波动慢， 微分时间应加长。
理想曲线两个波， 前高后低四比一。
一看二调多分析， 调节质量不会低。

PID是比例(P)、积分(I)、微分(D)控制算法，并不是必须同时具备这三种算法，也可以是PD,PI,甚至只有P算法控制。