【Python位运算】——左移操作（＜＜）右移操作＞＞

目录

左移操作

右移操作

其他博主的理解

应用——力扣题目78. 子集

解法

深度优先搜索

位运算

参考文献

---

左移操作

# 左移操作，左移一位相当于乘以b，a<

print(2<<3) # 2*2^3 = 16，2的二进制10，向左移动3位后10000
print(2<<1) # 2*2^1 = 4
print(3<<4) # 3*2^4 = 48,3的二进制为11，向左移动四位后110000

16
4
48

右移操作

# 右移操作，右移一位相当于除以b,a<
 

print(2>>3) # 2//2^3 = 0，2的二进制10，向右最多移动2位后，所以多移动无疑为0
print(2>>1) # 2*2^1 = 4，向右移动一位为01,
print(3>>4) # 3*2^4 = 48,3的二进制为11，向右移动四位后00
print(3>>1) # 3*2^4 = 48,3的二进制为11，向右移动一位后为01

0
1
0
1

其他博主的理解

 >> 和 <<都是位运算，对二进制数进行移位操作。
<< 是左移，末位补0，类比十进制数在末尾添0相当于原数乘以10，x<<1是将x的二进制表示左移一位，相当于原数x乘2。比如整数4在二进制下是100，4<<1左移1位变成1000(二进制)，结果是8。
>>是右移，右移1位相当于除以2。
而>>=和<<=，就是对变量进行位运算移位之后的结果再赋值给原来的变量，可以类比赋值运算符+=和-=可以理解。
比如x>>=2， 就是把变量x右移2位，再保留x操作后的值。

应用——力扣题目78. 子集

78. 子集——力扣题目

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

    1 <= nums.length <= 10
    -10 <= nums[i] <= 10
    nums 中的所有元素 互不相同

解法

https://leetcode-cn.com/problems/subsets/solution/hui-su-python-dai-ma-by-liweiwei1419/

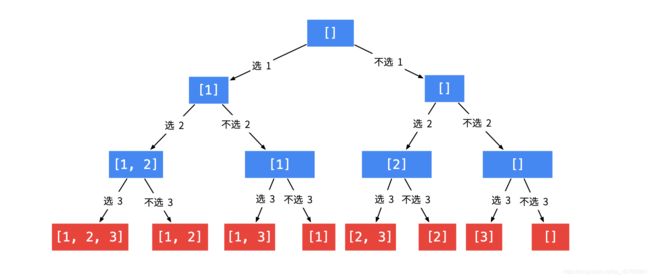
深度优先搜索

class Solution:
	# 深度优先搜索
	# 执行用时：36 ms, 在所有 Python3 提交中击败了85.39% 的用户
	def subsets(self, nums):
		res = []
		sub = []
		n = len(nums)
		def dfs(index,sub):
			if index == n:
				res.append(sub[:])
				return
			# 不选择index
			dfs(index+1,sub)
			# 选择
			sub.append(nums[index])
			dfs(index+1,sub)
			sub.remove(nums[index])
		dfs(0,sub)
		return res

位运算

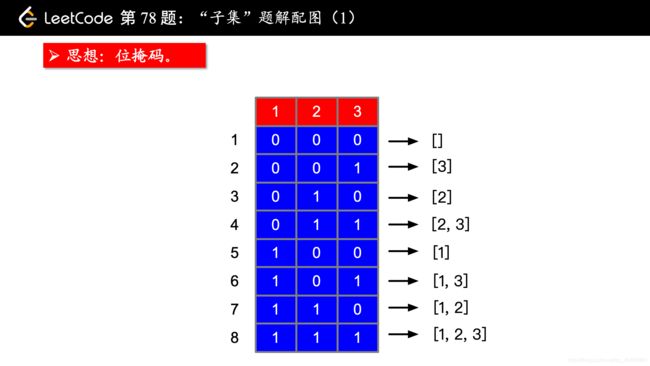
记原序列中元素的总数为 nnn。原序列中的每个数字 aia_iai​ 的状态可能有两种，即「在子集中」和「不在子集中」。我们用 111 表示「在子集中」，000 表示不在子集中，那么每一个子集可以对应一个长度为 nnn 的 0/10/10/1 序列，第 iii 位表示 aia_iai​ 是否在子集中。

例如，n=3，a={1,2,3}：

可以发现 0/1 序列对应的二进制数正好从 0 到2^（n - 1）。我们可以枚举 mask∈[0,2^(n−1)]，mask的二进制表示是一个 0/1 序列，我们可以按照这个 0/1 序列在原集合当中取数。当我们枚举完所有 2n2^n2n 个 mask\textit{mask}mask，我们也就能构造出所有的子集。

 这里其实有规律，首先是如果一个集合是由n个无重复数字组成的，那么他的子集个数为2^n，因此我们可以通过两次遍历，一个用于遍历子集数，一个用于遍历每个子集代表的二进制

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        size = len(nums)
        n = 1 << size
        res = []
        for i in range(n):
            cur = []
            for j in range(size):
                if i >> j & 1:
                    cur.append(nums[j])
            res.append(cur)
        return res

参考文献

https://zhidao.baidu.com/question/310628609.html

https://www.zhihu.com/question/397471252