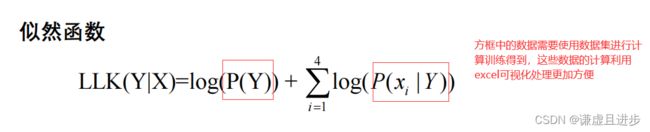朴素贝叶斯(Naive Bayes)
朴素贝叶斯是一个基于概率统计的机器学习算法,作用是用于多分类。
训练集包含已知分类类别的大量样本,每个样本具有n维特征,例如:已知一个人分类为胖或者瘦,有5个特征用于分类,这5个特征分别是体重、身高、年龄、鞋码、每天吃几碗饭。每个特征可能还有分等级,如鞋码分为L、XL等。
主要用到的数学知识有:条件概率、全概率公式、贝叶斯定理等。朴素贝叶斯对于具体的问题需要具体分析。
目录
一,基本的数学知识
1.1条件概率
1.2 全概率公式
1.3贝叶斯公式
二,具体例子实现二分类算法
2.1 独立分布、联合分布与条件分布的关系
2.2 应用贝叶斯公式
2.3 对概率计算公式取对数,从而连乘变为连加
三,python代码实现
3.1代码解析
3.1.1读取数据集
3.1.2 计算P(X|Y)
3.1.3模型数据计算结果解读
3.1.4模型的使用
3.2python代码
四,总结
一,基本的数学知识
1.1条件概率
概率:某类样本的数量与样本总量的比值称为频率,对频率求极限得到概率。
条件概率:首先对总的样本按照给定条件将合适的选出来,某类样本的数量与选出来的样本数量的比值极限就是条件概率。
1.2 全概率公式
由条件概率,可以得到:P(AB)=P(B)P(A|B)=P(A)P(B|A)。事件A由b1,b2,b3,……,bn等影响,全概率就是P(AB),其中B可以独立地分为B1,B2,……,Bn,将Bj作为条件累加得到。
1.3贝叶斯公式
贝叶斯公式就是对全概率公式的反驳,已知A发生的概率,求A发生是因为b1,b2,……,bn中b6引起的概率。
二,具体例子实现二分类算法
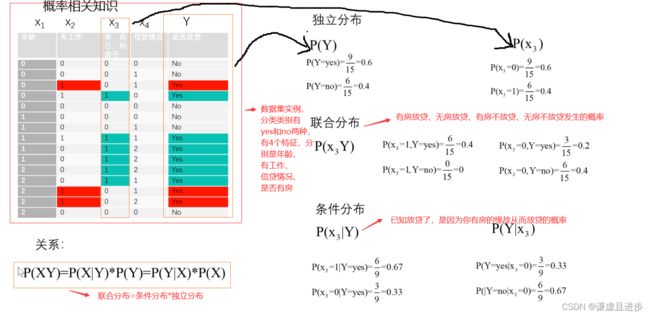
2.1 独立分布、联合分布与条件分布的关系
一共具有15个样本。朴素贝叶斯的情况用到了全概率公式,只是全概率公式的完备事件组只有一个。
2.2 应用贝叶斯公式
下图中的各种概率可以根据样本计算得到。
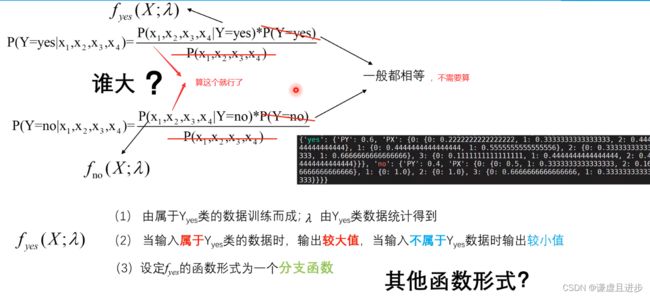
2.3 对概率计算公式取对数,从而连乘变为连加
作为机器学习的算法,必然少不了模型的训练,概率模型函数的训练就是依据已有的样本,把一些计算过程的固定参数进行计算保存。
对于数学来讲,上述模型还可以进一步进行简化。简化的理论如下:GMM分类模型就是进一步简化得到的结果。
三,python代码实现
3.1代码解析
3.1.1读取数据集
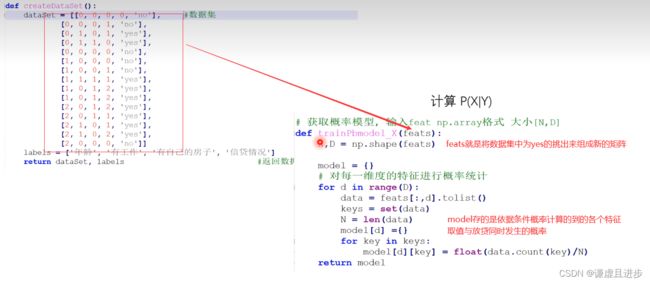
依据算法流程,首先将需要的数据利用一定的数据结构放入内存。或者利用excel可视化进行操作计算得到各种所需的数据结构也可行。
3.1.2 计算P(X|Y)
3.1.3模型数据计算结果解读
朴素贝叶斯最终需要计算一些概率,模型训练就是将要用到的各种参数进行计算并保存,当得到新样本时,将样本的特征矩阵代入就可以计算。
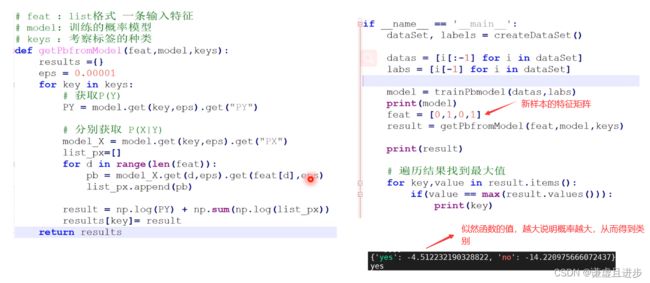
3.1.4模型的使用
3.2python代码
import numpy as np
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], #数据集,平面二维N×D
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['年龄', '有工作', '有自己的房子', '信贷情况'] #特征标签
return dataSet, labels #返回数据集和分类属性
# 获得 P(X|Y)
def trainPbmodel_X(feats):
N,D = np.shape(feats) #N个满足条件的样本,每个样本D个特征
model = {}
# 对每一维度的特征进行概率统计
for d in range(D):
data = feats[:,d].tolist() #获取所有样本每个特征所组成的列表
keys = set(data) # 列表变集合,实现去重,获取特征的取值个数,如年龄类别分为老中幼,那么keys里面存三个数据
N = len(data) #样本个数
model[d] ={}
for key in keys:
model[d][key] = float(data.count(key)/N)
return model
# datas: list格式 每个元素表示1个特征序列
# labs: list格式 每个元素表示一个标签
def trainPbmodel(datas,labs):
# 定义模型
model = {}
# 获取分类的类别
keys = set(labs)
for key in keys:
# 获得P(Y)
Pbmodel_Y = labs.count(key)/len(labs) #每个类别的概率
# 收集标签为Y的数据
index = np.where(np.array(labs)==key)[0].tolist() #[2, 3, 7, 8, 9, 10, 11, 12, 13],类别为Y的样本序号
feats = np.array(datas)[index] #[2, 3, 7, 8, 9, 10, 11, 12, 13],类别为Y的样本的特征矩阵
# print(index)
# print(feats)
# 获得 P(X|Y)
Pbmodel_X = trainPbmodel_X(feats)
# 模型保存
model[key]={}
model[key]["PY"] = Pbmodel_Y
model[key]["PX"] = Pbmodel_X
return model
# feat : list格式 一条输入特征
# model: 训练的概率模型
# keys :考察标签的种类
def getPbfromModel(feat,model,keys):
results ={}
eps = 0.00001
for key in keys:
# 获取P(Y)
PY = model.get(key,eps).get("PY")
# 分别获取 P(X|Y)
model_X = model.get(key,eps).get("PX")
list_px=[]
for d in range(len(feat)):
pb = model_X.get(d,eps).get(feat[d],eps)
list_px.append(pb)
result = np.log(PY) + np.sum(np.log(list_px))
results[key]= result
return results
if __name__ == '__main__':
'''实验一 自制贷款数据集'''
# 获取数据集
dataSet, labels = createDataSet()
# 截取数据和标签
datas = [i[:-1] for i in dataSet] # 特征矩阵
labs = [i[-1] for i in dataSet] #每个样本的类别1×N
# 获取标签种类
keys = set(labs) # keys是{'yes', 'no'},集合去掉相同的标签
# 进行模型训练
model = trainPbmodel(datas,labs)
print(model)
# 根据输入数据获得预测结果
feat = [0,0,0,1]
result = getPbfromModel(feat,model,keys)
print(result)
# 遍历结果找到概率最大值进行数据
for key,value in result.items():
if(value == max(result.values())):
print("预测结果是",key)
四,总结
朴素贝叶斯算法最终算的是一系列概率,这些概率与样本的特征有关,如果有N个类别就需要计算N个概率,其中概率最大的就是样本所属类别。
在计算这些概率的时候使用到了贝叶斯定理,贝叶斯公式中的个别数据需要使用数据集计算的到,也就是模型参数的训练。这些参数如下: