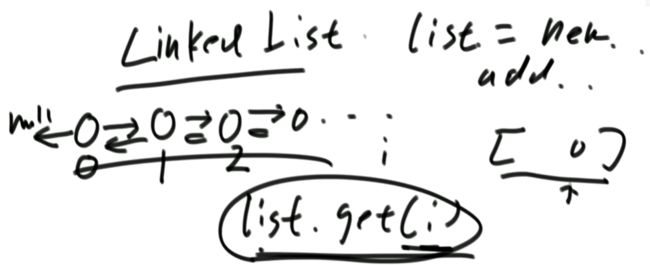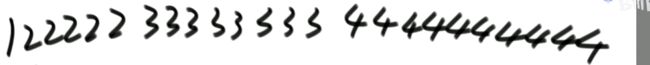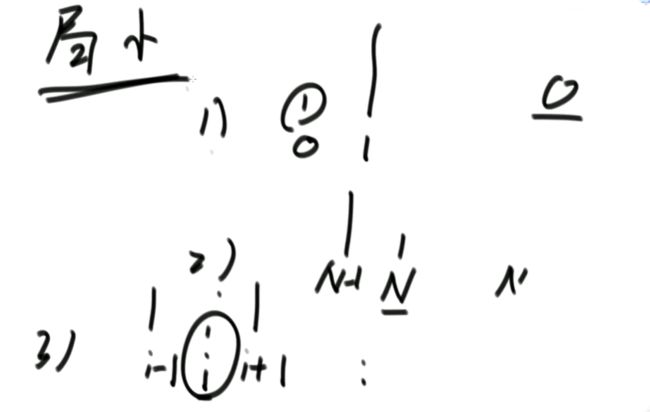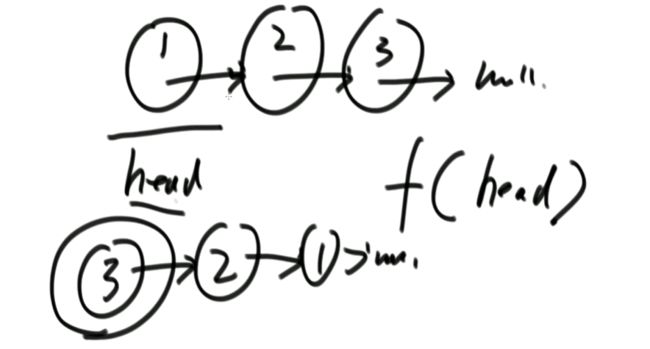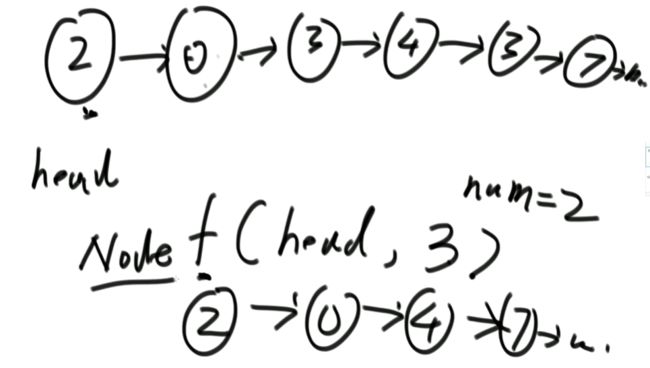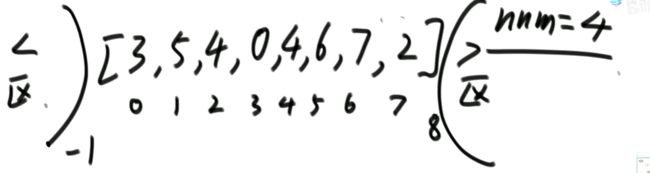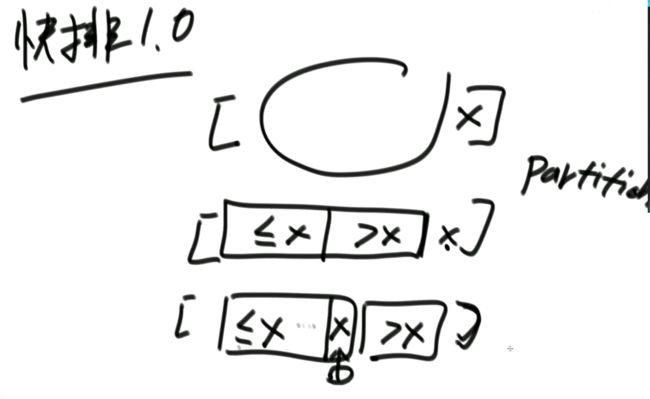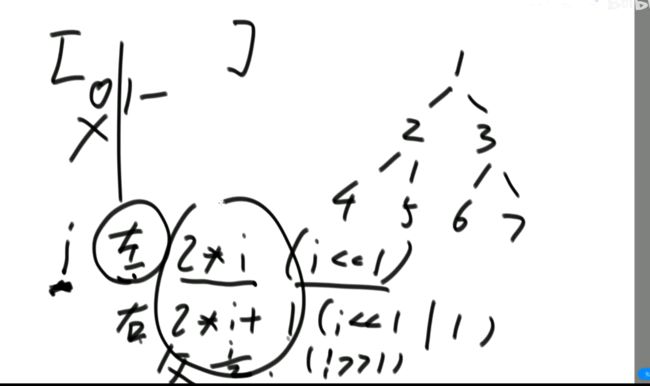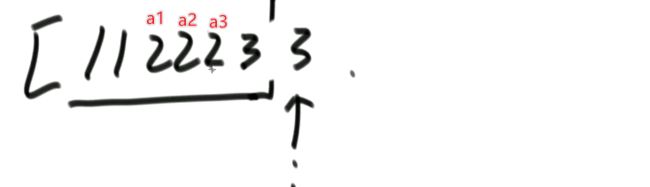左神算法（一）上修改版

​

序言：

左神（左程云）所讲课程有两套，一套为马士兵，一套为牛客。两套体系不好区分。
有基础班和训练营。基础班是基础，训练营前两节属于提升班（进阶版），提升班还是基础，不过难度比基础班高一些，建议掌握基础班和提升版的基础上学习训练营。
以下为 硬核！一周刷爆LeetCode，算法大神（左程云）耗时112天打造出算法与数据结构基础到高级全家桶教程+大厂面试真题详解_哔哩哔哩_bilibili
的 P2到P17

左神算法（一）上修改版

左神算法（一）下修改版

左神算法（二）

一、认识复杂度、对数器、二分法与异或运算

1.评估算法优劣的核心指标是什么？

时间复杂度（流程决定）

额外空间复杂度（流程决定）

常数项时间（实现细节决定）

2.何为常数时间的操作？

​

（1）解释：

如果一个操作的执行时间不以具体样本量为转移,每次执行时间都是固定时间。称这样的操作为常数时间的操作。
​​

（2）常见的常数时间的操作：

• 常见的算术运算(+、-、*、/、%等)
• 常见的位运算(>>、>>>、<<、&、^等)
• 赋值、比较、自增、自减操作等
• 数组寻址操作

总之,执行时间固定的操作都是常数时间的操作。
反之,执行时间不固定的操作,都不是常数时间的操作。

拓展

位运算：
>>：带符号右移
>>>：不带符号右移

可见他人的博客：
Java中位运算的解析
java的位运算解析（&/|/~/^/>>/<>>）

解释：
原来的数字最高位就是符号位，带符号右移就是把原来的数字都右移1位后，最高位补一个原来数字的符号位。不带符号右移就是把原来的数字都右移1位后，最高位补一个0。

对于“带符号右移和不带符号右移”举例：
若一个整型数字32位：000000…11000
带符号右移就变为XX：000000…01100
不带符号右移XXXXX：000000…01100

举例：LinkedList就不是常数时间的操作：

​​​​

数组底层是一个连续区间，可以算出偏移量取出来。而LinkedList底层是指针移动找下一个节点，不是连续期间，此时list.get(i)就不是一个常数时间的操作，它需要遍历才行。

时间复杂度就是衡量这个流程中发生了多少次常数操作。

对于“时间复杂度就是衡量这个流程中发生了多少次常数操作”的举例：选择排序

一个无序数组arr，0到N-1位置找最小值与0位置交换
1到N-1位置找最小值与1位置交换
…
每行都要看+比，再来一次交换。



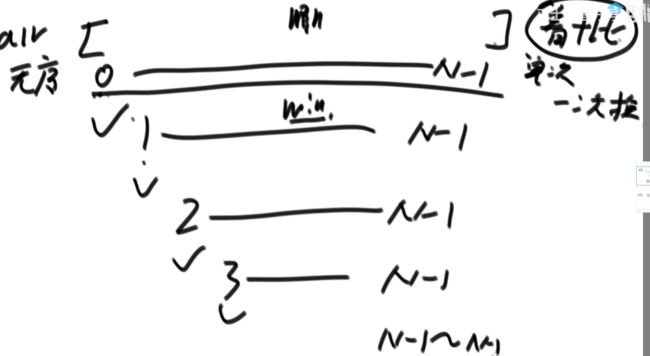
常数操作 num
num = N * (看+比)+交换 + (N-1) * (看+比)+交换+…
看=1，比=1，交换=1.其中有时交换会发生，有时交换不会发生，有时交换为0有时为1.时间复杂度是不计算常数项的，所以交换可以不精确。
所以 num = N * (1+1)+1 + (N-1) * (1+1)+1 + …
num = 2 * (N+N-1+…+1)+N

N+N-1+…+1为等差数列。
等差数列可以写为：

所以num=下图

又时间复杂度不考虑常数项、低次项和高次项系数。计算时间复杂度时不要太在意时间复杂度常数项的多少，粗略计算就可以，因为反正最后也不会考虑常数项。所以 选择排序的时间复杂度为N的平方。

选择排序的最好、最坏时间复杂度都是N的平方。

3.如何确定算法流程的总操作数量与样本数量之间的表达式关系？

1. 想象该算法流程所处理的数据状况,要按照最差情况来。
2. 把整个流程彻底拆分为一个个基本动作,保证每个动作都是常
   数时间的操作。
3. 如果数据量为N,看看基本动作的数量和N是什么关系。

对于第二点拆分到位的解释：
就如上方选择排序的举例，其中的看+比+换都是最基本的动作单位。

4.如何确定算法流程的时间复杂度？

当完成了表达式的建立,只要把最高阶项留下即可。低阶项都去掉,
高阶项的系数也去掉。
记为:O(忽略掉系数的高阶项)

当样本量足够大的时候，即N趋向于很大很大的时候，除了高次项其他都不重要了。

举例：
两个表达式，然而当N足够大的时候，很明显N的平方的表达式时间复杂度是小于N的三次方的表达式的时间复杂度。

5.时间复杂度的意义

抹掉了好多东西,只剩下了一个最高阶项啊…
那这个东西有什么意义呢?
时间复杂度的意义在于：
当我们要处理的样本量很大很大时,我们会发现低阶项是什么不是最重要的;每一项的系数是什么不是最重要的。真正重要的就是最高阶项是什么。
这就是时间复杂度的意义,它是衡量算法流程的复杂程度的一种指标,该指标只与数据量有关.与过程之外的优化无关。

6.通过三个具体的例子，来实践一把时间复杂度的估算

选择排序、冒泡排序、插入排序的时间复杂度都是O(N ^ 2)。选择排序，冒泡排序的时间复杂度不会因样本数据的状态而影响时间复杂度，而插入排序的时间复杂度会受到样本数据状态的影响。

（1）选择排序

过程：
arr[0 ~ N-1]范围上,找到最小值所在的位置，然后把最小值交换到0位置。
arr[1 ~ N-1]范围上,找到最小值所在的位置，然后把最小值交换到1位置。
arr[2 ~ N-1]范围上,找到最小值所在的位置，然后把最小值交换到2位置。
…
arr[N-1 ~ N-1])范围上,找到最小值位置，然后把最小值交换到N-1位置。

估算：
很明显,如果arr长度为N，每一步常数操作的数量如等差数列一般。所以，
总的常数操作数量 = a * (n ^ 2) + bn + c（a、b、c都是常数）
所以选择排序的时间复杂度为O(N ^ 2)。

相关概念、解释上面已经解释，代码如下：

package class01;

import java.util.Arrays;

public class Code01_SelectionSort {

	// 选择排序主方法
	public static void selectionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		// 0 ~ N-1  找到最小值，在哪，放到0位置上
		// 1 ~ n-1  找到最小值，在哪，放到1 位置上
		// 2 ~ n-1  找到最小值，在哪，放到2 位置上
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标 
				minIndex = arr[j] < arr[minIndex] ? j : minIndex;
			}
			swap(arr, i, minIndex);
		}
	}

	// 选择排序的交换数字方法
	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

	// 其他方法都是对数器的方法
	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		// Math.random()   [0,1)  
		// Math.random() * N  [0,N)
		// (int)(Math.random() * N)  [0, N-1]
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			// [-? , +?]
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			selectionSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		selectionSort(arr);
		printArray(arr);
	}

}

（2）冒泡排序

过程:
在arr[0 ~ N-1]范围上，arr[0]和arr[1]谁大谁来到1位置；arr[1]和arr[2]谁大谁来到2位置…arr[N - 2]和arr[N - 1]谁大谁来到N-1位置。
在arr[0 ~ N-2]范围上，重复上面的过程，但最后一步是arr[N - 3]和arr[N - 2]谁大谁来到N-2位置。
在arr[0 ~ N-3]范围上，重复上面的过程，但最后一步是arr[N - 4]和arr[N - 3]谁大谁来到N-3位置。
…
最后在arr[0 ~ 1]范围上，重复上面的过程，但最后一步是arr[0]和arr[1]谁大谁来到1位置。

估算：
很明显,如果arr长度为N.每一步常数操作的数量,依然如等差数列一般，所以,总的常数操作数量=a(N ^ 2) + b * N + c（a、b、c都是常数）
所以冒泡排序的时间复杂度为O(N^2)。

具体案例：

第一轮0位置到5位置比较，选出最大值到5位置，见下面的步骤（第二行为下标，第一行为值。）：

0位置与1位置比较大小，0位置大于1位置则交换两个值，由上图得下图。

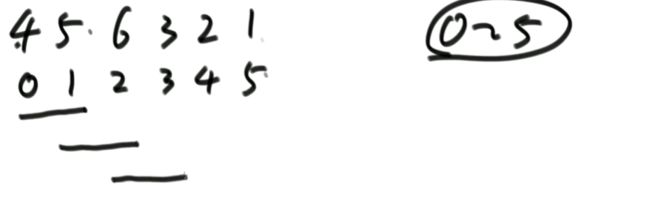
1位置和2位置比较，5<6所以不交换。
2位置和3位置比较，3<6所以交换，见下图。

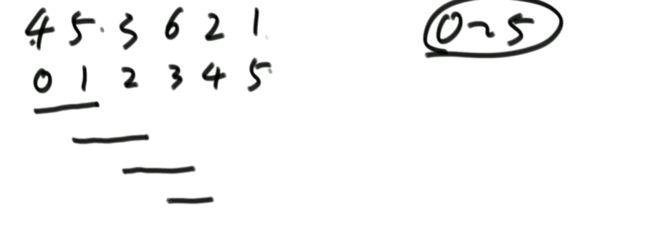
3位置和4位置比较，由上图知，2<6，所以交换。4位置和5位置比较，由上图知，1<6，所以交换。两次交换结果如下。

第一轮结束后最后成了上面这样，最大值选出来了。

第二轮0到4位置比较，选出第二大值到4位置。
…

假设有N个数字，冒泡排序是第一次进行N-1次比较，选取最大值放到N-1位置；第二次进行N-2次比较，选取第二大值放到N-2位置…所以冒泡排序的时间复杂度是O(N ^ 2)。

冒泡排序的代码如下：

package class01;

import java.util.Arrays;

public class Code02_BubbleSort {

	// 冒泡排序主方法
	public static void bubbleSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		// 0 ~ N-1
		// 0 ~ N-2
		// 0 ~ N-3
		for (int e = arr.length - 1; e > 0; e--) { // 0 ~ e
			for (int i = 0; i < e; i++) {
				// 两数相同则不交换。若为>=，则两数相同交换，两数相同交换多此一举。
				if (arr[i] > arr[i + 1]) {
					swap(arr, i, i + 1);
				}
			}
		}
	}

	// 交换arr的i和j位置上的值
	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {		
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			bubbleSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		bubbleSort(arr);
		printArray(arr);
	}

}

（3）插入排序

过程:
想让arr[0 ~ 0]上有序，这个范围只有一个数，当然是有序的。
想让arr[0 ~ 1]上有序，所以从arr[1]开始往前看，如果arr[1] < arr[0]就交换。否则什么也不做。
想让arr[0 ~ i]上有序，所以从arr[i]开始往前看，arr[i]这个数不停向左移动，一直移动到左边的数字不再比自己大，停止移动。
最后一步,想让arr[0 ~ N-1]上有序，arr[N - 1]这个数不停向左移动，一直移动到左边的数字不再比自己大,停止移动。
估算时发现这个算法流程的复杂程度,会因为数据状况的不同而不同，你发现了吗?

具体案例：
0到0位置上有序，如下图：

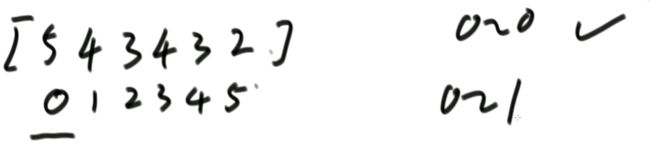
0到1位置上有序，如下图：

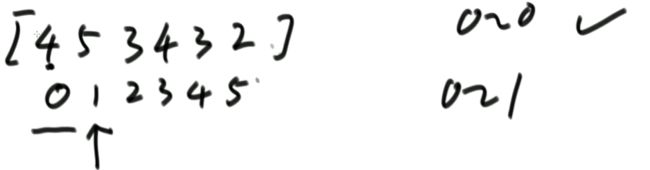
0到2位置上有序，2位置的3和1位置比较并交换，然后和0位置的4比较并交换，如下图：


…

上面是倒数第二步…

插入一个笑话：这类似于打牌，新拿一张牌，按顺序排大小，一个学生并不理解这个例子，说：我打牌是把质数放在左边，非质数放在右边。

注意：这个算法的时间复杂度会受到样本数据的初始状况影响

举例—算法的时间复杂度会受到样本数据的初始状况影响：

好的情况：初始数据有序，见下图

如上图，0到1位置比较，2比较1，有序；
0到2位置比较，3比较2，有序，此时3就不比较1了，且没有发生交换；
…
这就和上面的举例有了差距，此时时间复杂度是O(N)。

差的情况：见下图

此时时间复杂度是O(N ^ 2）。

总结：然而我们考虑时间复杂度要拿最差情况作为时间复杂度的计算。

代码如下：

package class01;

import java.util.Arrays;

public class Code03_InsertionSort {

	public static void insertionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		// 不只1个数
		for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
			// j + 1就是i
			// arr[j] > arr[j + 1]	就是两数相等也不交换。若为 >=，则两数相等也交换，这是多此一举！
			for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
				swap(arr, j, j + 1);
			}
		}
	}

	// i和j是一个位置的话，会出错
	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		// Math.random() -> [0,1) 所有的小数，等概率返回一个
		// Math.random() * N -> [0,N) 所有小数，等概率返回一个
		// (int)(Math.random() * N) -> [0,N-1] 所有的整数，等概率返回一个
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; // 长度随机
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100; // 随机数组的长度0～100
		int maxValue = 100;// 值：-100～100
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(maxSize, maxValue);
			int[] arr1 = copyArray(arr);
			int[] arr2 = copyArray(arr);
			insertionSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
				// 打印arr1
				// 打印arr2
				succeed = false;
				for (int j = 0; j < arr.length; j++) {
					System.out.print(arr[j] + " ");
				}
				System.out.println();
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		insertionSort(arr);
		printArray(arr);
	}

}

7.如何确定算法流程的总操作数量与样本数量之间的表达式关系

1. 想象该算法流程所处理的数据状况,要按照最差情况来。
2. 把整个流程彻底拆分为一个个基本动作,保证每个动作都是常
   数时间的操作。
3. 如果数据量为N,看看基本动作的数量和N是什么关系。

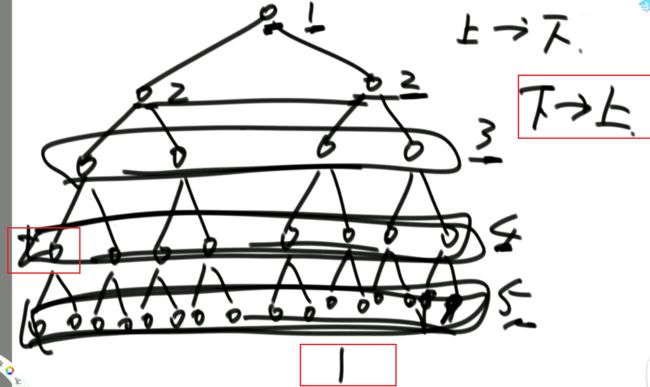
O为最差时间复杂度写法。上面第一个是最好时间复杂度写法；第二个是平均时间复杂度写法；第三个是最差时间复杂度写法。

8.注意

1. 算法的过程和具体的语言是无关的。
2. 想分析一个算法流程的时间复杂度的前提，是对该流程非常熟悉。
3. 一定要确保在折分算法流程时，拆分出来的所有行为都是常数时间的操作。这意味着你写算法时对自己的用过的每一个系统api，都非常的熟悉。否则会影响你对时间复杂度的估算。

9.额外空间复杂度

​​​​​​​​​​​​​​​你要实现一个算法流程，在实现算法流程的过程中，你需要开辟一些空间来支持你的算法流程。
作为输入参数的空间，不算额外空间。
作为输出结果的空间，也不算额外空间。
因为这些都是必要的、和现实目标有关的。所以都不算。
但除此之外，你的流程如果还需要开辟空间才能让你的流程继续下去。这部分空间就是额外空间。
如果你的流程只需要开辟有限几个变量,额外空间复杂度就是O(1)

O(1)：常数操作
流程中不需要开辟新的空间，有限几个变量就可以完成事情，额外空间复杂度就是O(1)
需要开辟额外数组，额外空间复杂度是O(N)。

额外空间的解释：和功能无关的必须申请的空间。

举例：给你一个数组arr，然后要求复制这个数组返回给用户，我们在流程中必须new一个新数组，然而这个数组是必须的，是被要求返回的，所以这个数组不属于额外空间。即作为输入参数的和输出结果的空间不算额外空间。
选择，冒泡，插入都是申请了有限几个变量，所以他们的额外空间复杂度都是O(1)

10.算法流程的常数项

我们会发现，时间复杂度这个指标，是忽略低阶项和所有常数系数的。
难道同样时间复杂度的流程，在实际运行时候就一样的好吗?

当然不是。

时间复杂度只是一个很重要的指标而已如果两个时间复杂度一样的算法,
你还要去在时间上拼优劣，就进入到拼常数时间的阶段,简称拼常数项。

算法流程的常数项的比拼方式：
放弃理论分析，生成随机数据直接测。
为什么不去理论分析?
不是不能纯分析，而是没必要。因为不同常数时间的操作，虽然都是固定时间，但还是有快慢之分的。
比如，位运算的常数时间原小于算术运算的常数时间，这两个运算的常数时间又远小于数组寻址的时间。
所以如果纯理论分析，往往会需要非常多的分析过程。都已经到了具体细节的程度，莫不如交给实验数据好了。

当时间复杂度相同时，就需要考虑常数项了，然而我们没必要进行理论分析，而是直接进行样本测试。因为当过程拆分到位时，每个基本的常数动作也是有时间快慢的。

±运算时间是比*/快的。±运算时间没有位运算快。

位运算符号：
| ：或

11.面试、比赛、刷题中，一个问题的最优解是什么意思？

一般情况下，认为解决一个问题的算法流程，在时间复杂度的指标上，一定要尽可能的低，先满足了时间复杂度最低这个指标之后，使用最少的空间的算法流程，叫这个问题的最优解。
一般说起最优解都是忽略掉常数项这个因素的，因为这个因素只决定了实现层次的优化和考虑，而和怎么解决整个问题的思想无关。

一般正规的比赛、面试是不考虑常数项时间的。

12.常见的时间复杂度

13.算法和数据结构学习的大脉络

（1）知道怎么算的算法
如：3+3=6

（2）知道怎么试的算法
如：暴力递归，之后寻求更优解

14.对数器

你在网上找到了某个公司的面试题，你想了好久，感觉自己会做，但是你找不到在线测试，你好心烦…
你和朋友交流面试题,你想了好久,感觉自己会做,但是你找不到在线测试，
你好心烦…
你在网上做笔试，但是前几个测试用例都过了，突然一个巨大无比数据量来了，结果你的代码报错了，如此大的数据量根本看不出哪错了，你好心烦…

对数器怎么用：
1.你想要测的方法a
2.实现复杂度不好但是容易实现的方法b
3.实现一个随机样本产生器
4.把方法a和方法b跑相同的随机样本看看得到的结果是否一样
5.如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对
方法a和方法b
6.当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

**举例：**选择排序的代码拿过来

package class01;

import java.util.Arrays;

public class Code01_SelectionSort {

	// 选择排序主方法
	public static void selectionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		// 0 ~ N-1  找到最小值，在哪，放到0位置上
		// 1 ~ n-1  找到最小值，在哪，放到1 位置上
		// 2 ~ n-1  找到最小值，在哪，放到2 位置上
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标 
				minIndex = arr[j] < arr[minIndex] ? j : minIndex;
			}
			swap(arr, i, minIndex);
		}
	}

	// 选择排序的交换数字方法
	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

	// 其他方法都是对数器的方法
	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// 产生随机数
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		// Math.random()   [0,1)  
		// Math.random() * N  [0,N)
		// (int)(Math.random() * N)  [0, N-1]
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			// [-? , +?]
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			// 自己写的排序算法去排序一个数组
			selectionSort(arr1);
			// 系统的排序算法去排序一个数组
			comparator(arr2);
			// 如果两个数组相等，证明自己写的排序算法正确
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		// 如果结果不正确，我们可以考虑把maxSize调小一点观察
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		selectionSort(arr);
		printArray(arr);
	}

}

15.认识二分法

经常见到的类型是在一个有序数组上，开展二分搜索。
但有序真的是所有问题求解时使用二分的必要条件吗?
不
只要能正确构建左右两侧的淘汰逻辑,你就可以二分。

使用场景：

（1）在一个有序数组中，找某个数是否存在
（2）在一个有序数组中，找>=某个数最左侧的位置
（3）在一个有序数组中，找<=某个数最右侧的位置
（4）局部最小值问题

举例：

（1）给定一个有序数组，寻找数组中的7是否存在。

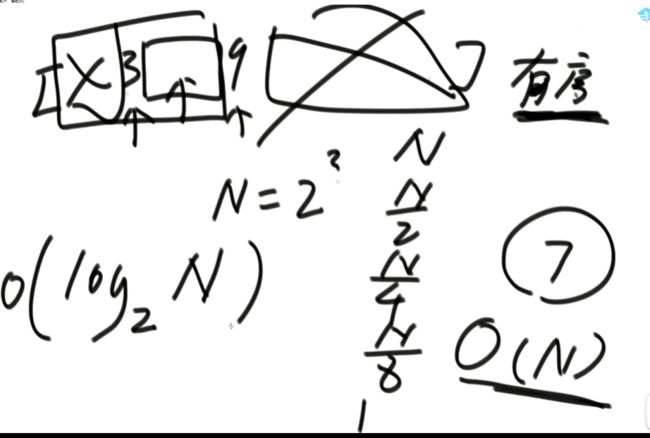
不断二分下，时间复杂度变化：N => 二分之N => 四分之N => 八分之N

因此，最后的时间复杂度是O(logN)

代码如下：

package class01;

import java.util.Arrays;

public class Code04_BSExist {

	public static boolean exist(int[] sortedArr, int num) {
		if (sortedArr == null || sortedArr.length == 0) {
			return false;
		}
		int L = 0;
		int R = sortedArr.length - 1;
		int mid = 0;
		// L..R
		while (L < R) { // L..R 至少两个数的时候
			// 若下方写成 mid = (L + R) / 2
			// L为10亿	R为18亿	L和R为下标
			// mid就溢出了，不安全！	安全可写成 mid = L + (R - L) / 2
			// 一个数N / 2 等价于	N >> 1 （N的二进制带符号右移1位）
			// 一个数N * 2 等价于	N << 1 （N的二进制带符号左移1位）
			// 一个数N * 2 + 1 等价于	((N << 1) | 1) （N的二进制带符号左移1位再或一下1， | 为或的意思）
			// 思考：N * 2 - 1 呢
			// 下方这么写是因为位运算比除运算快
			mid = L + ((R - L) >> 1);	// mid = (L + R) / 2
			if (sortedArr[mid] == num) {
				return true;
			} else if (sortedArr[mid] > num) {
				R = mid - 1;
			} else {
				L = mid + 1;
			}
		}
		return sortedArr[L] == num;
	}
	
	// for test
	public static boolean test(int[] sortedArr, int num) {
		for(int cur : sortedArr) {
			if(cur == num) {
				return true;
			}
		}
		return false;
	}
	
	
	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}
	
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 10;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(maxSize, maxValue);
			Arrays.sort(arr);
			int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
			if (test(arr, value) != exist(arr, value)) {
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

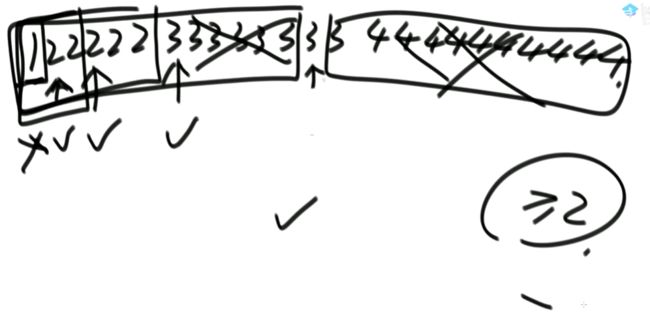
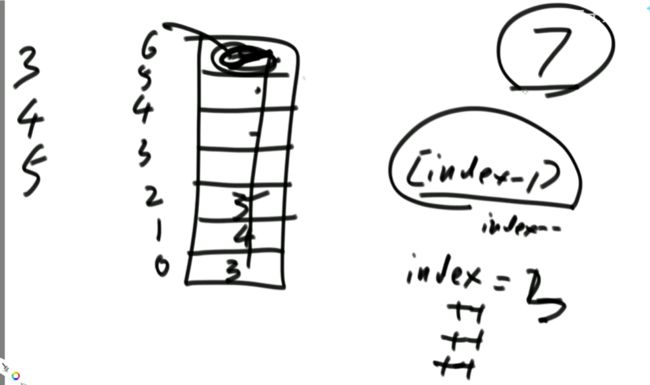
（2）给定一个有序数组，寻找>=2最左侧的位置

有序数组如下图：


代码如下：

package class01;

import java.util.Arrays;

public class Code05_BSNearLeft {

	// 在arr上，找满足>=value的最左位置
	public static int nearestIndex(int[] arr, int value) {
		int L = 0;
		int R = arr.length - 1;
		int index = -1; // 记录最左的对号
		while (L <= R) { // 至少一个数的时候
			int mid = L + ((R - L) >> 1);
			if (arr[mid] >= value) {
				index = mid;
				R = mid - 1;
			} else {
				L = mid + 1;
			}
		}
		return index;
	}

	// for test
	public static int test(int[] arr, int value) {
		for (int i = 0; i < arr.length; i++) {
			if (arr[i] >= value) {
				return i;
			}
		}
		return -1;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}
	
	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 10;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(maxSize, maxValue);
			Arrays.sort(arr);
			int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
			if (test(arr, value) != nearestIndex(arr, value)) {
				printArray(arr);
				System.out.println(value);
				System.out.println(test(arr, value));
				System.out.println(nearestIndex(arr, value));
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

（3）有序数组中，找<=某个数最右侧的位置

package class01;

import java.util.Arrays;

public class Code05_BSNearRight {

	// 在arr上，找满足<=value的最右位置
	public static int nearestIndex(int[] arr, int value) {
		int L = 0;
		int R = arr.length - 1;
		int index = -1; // 记录最右的对号
		while (L <= R) {
			int mid = L + ((R - L) >> 1);
			if (arr[mid] <= value) {
				index = mid;
				L = mid + 1;
			} else {
				R = mid - 1;
			}
		}
		return index;
	}

	// for test
	public static int test(int[] arr, int value) {
		for (int i = arr.length - 1; i >= 0; i--) {
			if (arr[i] <= value) {
				return i;
			}
		}
		return -1;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 10;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(maxSize, maxValue);
			Arrays.sort(arr);
			int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
			if (test(arr, value) != nearestIndex(arr, value)) {
				printArray(arr);
				System.out.println(value);
				System.out.println(test(arr, value));
				System.out.println(nearestIndex(arr, value));
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

（4）局部最小值问题

上图的解释：

对于0 1

0就是局部最小的位置，因为0的右边都比0大，且0的左边没数

对于2 1

1就是局部最小的位置，因为1的左边都比1大，且1的右边没数

对于i -1 i i+1

i

举例：一个无序数组arr，数组为arr[0…N-1]，相邻不相等，寻求局部最小值。

解法：可以考虑使用二分法。
解析：

0位置和1位置比大小，N-2和N-1位置比大小。

若0位置<1位置，N-2位置小于N-1位置，则最小值一定在1位置到N-2位置中。我们再找0和N-1的中间位置，也就是进行二分，之后再二分。

二分法不一定要有序才能二分。

代码如下：

package class01;

public class Code06_BSAwesome {

	public static int getLessIndex(int[] arr) {
		if (arr == null || arr.length == 0) {
			return -1; // no exist
		}
		if (arr.length == 1 || arr[0] < arr[1]) {
			return 0;
		}
		if (arr[arr.length - 1] < arr[arr.length - 2]) {
			return arr.length - 1;
		}
		int left = 1;
		int right = arr.length - 2;
		int mid = 0;
		while (left < right) {
			mid = (left + right) / 2;
			if (arr[mid] > arr[mid - 1]) {
				right = mid - 1;
			} else if (arr[mid] > arr[mid + 1]) {
				left = mid + 1;
			} else {	// 这种情况即：arr[mid - 1] < arr[mid] < arr[mid + 1]。即局部最小值
				return mid;
			}
		}
		return left;
	}

}

16.认识异或运算

异或运算：相同为0，不同为1。
同或运算：相同为1，不同为0。
能长时间记住的概率接近0。
所以，异或运算就记成无进位相加。

举例： 6 ^ 7 = ? （^是异或的意思）

6的二进制：110

7的二进制：111

6 ^ 7 =

110

^

111

=001

=1

异或运算就记成无进位相加

思考：做一个数学计算器，包括各种数学符号

异或运算的性质

（1）0 ^ N == N；N ^ N == 0
（2）异或运算满足交换律和结合率

上面的两个性质用无进位相加来理解就非常的容易

交换律和结合律举例：a ^ b ^ c == a ^ c ^ b

（1）题目一：如何不用额外变量交换两个数

举例：int a = 甲，int b = 乙 令 int a =乙，int b = 甲

解法：

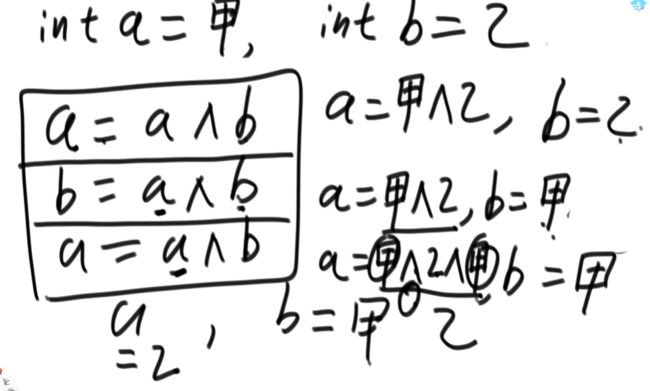
提示： a = a ^ b 此行结束b的值不变
b = a ^ b 此行结束a的值不变
a = a^ b 此行结束完成要求

代码如下：

  		int a = 6;
		int b = -1000;
		
		System.out.println(a);
		System.out.println(b);
		
		
		a = a ^ b;
		b = a ^ b;
		a = a ^ b;

		System.out.println(a);
		System.out.println(b);

  // 交换arr的i和j位置上的值
	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

（2）注意

如果a,b相等也对，因为int型的a=b=6，但是它们的内存是两个东西，如下：

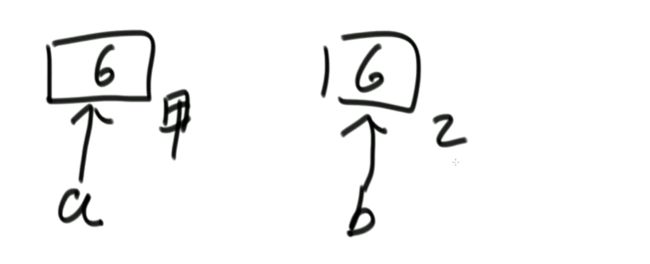
  		int a = 6;
		int b = 6;
		
		System.out.println(a);
		System.out.println(b);

		a = a ^ b;
		b = a ^ b;
		a = a ^ b;

		System.out.println(a);
		System.out.println(b);

下面的情况使用异或就错了：

	int[] arr = {3,1,100};

    System.out.println(arr[0]);
    System.out.println(arr[2]);
		
	swap(arr, 0, 0);    // 内存区域相同，这就错了
		
	System.out.println(arr[0]);
	System.out.println(arr[2]);
		
	
	public static void swap (int[] arr, int i, int j) {
		// arr[0] = arr[0] ^ arr[0];
		arr[i]  = arr[i] ^ arr[j];
		arr[j]  = arr[i] ^ arr[j];
		arr[i]  = arr[i] ^ arr[j];
	}
	
	

结论：值相同没关系，但内存必须不同。

（3）题目二：一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这个数。

解法：
int eor = 0; 然后把其中的所有数异或起来，eor结果就是出现奇数次的数。

代码如下：

  	// arr中，只有一种数，出现奇数次
	public static void printOddTimesNum1(int[] arr) {
		int eor = 0;
		for (int i = 0; i < arr.length; i++) {
			eor ^= arr[i];
		}
		System.out.println(eor);
	}

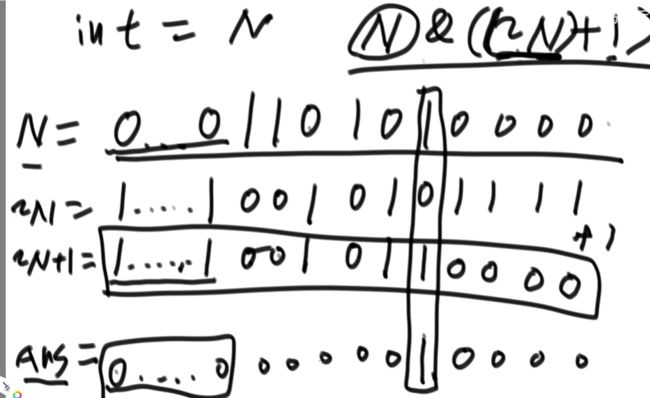
（4）题目三：怎么把一个int类型的数，提取出最右侧的1来

解法：N与上(N取反+1)

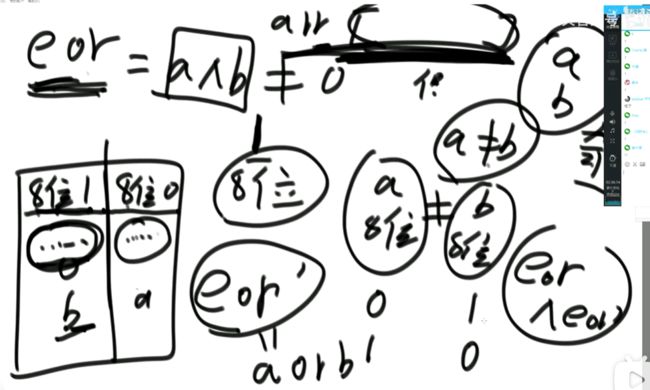
（5）题目四：一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这两种数。

解法：创建变量 int eor = 0; 设a,b为出现奇数次的数，arr数组。eor异或arr数组中所有的数。

eor = a ^ b;且eor != 0。因为 N ^ N == 0，所以eor != 0 eor != 0 说明eor的二进制的某个位置上有1，假设第8位是1。则a的第8位和b的第8位是不一样的。此时我们从这个角度再次分类数组，一类数是第8位为0的，一类数是第8位为1的。

int eor’ = 0; eor ’ = eor’ ^ 所有第8位是0或1的数 此时的eor ’ = a 或 b

eor = eor ^ eor’ 此时的eor就是另外一个 即eor = b 或 a

这里的第8位为1是假设的，我们找只需要找eor的最右侧的1。eor的二进制最右侧的1找法见上述的第（4）点。

这里也不一定非要选最右侧的1，只需要某一位上a和b不同即可。下图即为选中第三位的1：

代码如下：

	// arr中，有两种数，出现奇数次
	public static void printOddTimesNum2(int[] arr) {
		int eor = 0;
		for (int i = 0; i < arr.length; i++) {
			eor ^= arr[i];
		}
		// 上述代码结束后eor == a ^ b
		// a 和 b是两种数
		// eor != 0
		// eor最右侧的1，提取出来
		// eor :     00110010110111000
		// rightOne :00000000000001000
		int rightOne = eor & (~eor + 1); // 提取出最右的1 	int rightOne = eor & (-eor);这种写法好像也可以，好像！
		
		// int eor’ = 0; eor ’ = eor’ ^ 所有第8位是0或1的数 此时的eor ’ = a 或 b
		// eor = eor ^ eor’ 此时的eor就是另外一个 即eor = b 或 a
		int onlyOne = 0; // onlyOne就是eor'
		for (int i = 0 ; i < arr.length;i++) {
			//  arr[i] =  111100011110000
			// rightOne=  000000000010000
			if ((arr[i] & rightOne) != 0) {	// eor’ ^ 所有第8位是0或1的数
				onlyOne ^= arr[i];
			}
		}
		// 此时的eor ’ = a 或 b，即此时的onlyOne = a或b。	eor = eor ^ eor’ 
		// 此时的eor就是另外一个 即eor = b 或 a
		System.out.println(onlyOne + " " + (eor ^ onlyOne));
	}

（6）题目五：输出二进制中1的个数

代码如下：

    // 数出二进制中1的个数
	public static int bit1counts(int N) {
		int count = 0;

		while(N != 0) {	//	初始数字N：011011010000
			int rightOne = N & ((~N) + 1);	//   rightOne = 000000010000     1  第一个1就提取出来了
			count++;
			N ^= rightOne;		//   N = 011011000000	这就把最右边的1也就是提取出来的第一个1抹掉了（异或是无进位相加）
			// N -= rightOne(N是负数这样写就错了，所以写成N ^= rightOne;)	// 之后不断抹去1，又有count ++ .抹掉一个1，count+1.这就数出来1的个数
		}

		return count;
		
	}

二、链表结构、栈、队列、递归行为、哈希表和有序表

提示：程序员代码面试指南一书默认懂了所有的基础再看

1.单向链表

2.双向链表

3.单向链表和双向链表的最简单的练习

链表相关的问题几乎都是coding的问题。这里就是熟悉结构，链表还有哪些常见面试题，后续有专门一节来系统学习。

（1） 单向链表和双向链表如何反转

单向链表反转：

  public static class Node {
		public int value;
		public Node next;

		public Node(int data) {
			value = data;
		}
	}

    //  head
	//   a    ->   b    ->  c  ->  null
	//   c    ->   b    ->  a  ->  null
	public static Node reverseLinkedList(Node head) {
		Node pre = null;
		Node next = null;
		while (head != null) {
			next = head.next;    // next指针就是记录一下位置

			head.next = pre;
			pre = head;

			head = next;
		}
		return pre;
	}

    public static Node testReverseLinkedList(Node head) {
		if (head == null) {
			return null;
		}
		ArrayList<Node> list = new ArrayList<>();
		while (head != null) {
			list.add(head);
			head = head.next;
		}
		list.get(0).next = null;
		int N = list.size();
		for (int i = 1; i < N; i++) {
			list.get(i).next = list.get(i - 1);
		}
		return list.get(N - 1);
	}

双向链表反转：

  public static class DoubleNode {
		public int value;
		public DoubleNode last;
		public DoubleNode next;

		public DoubleNode(int data) {
			value = data;
		}
	}

    public static DoubleNode reverseDoubleList(DoubleNode head) {
		DoubleNode pre = null;
		DoubleNode next = null;
		while (head != null) {
			next = head.next;// next指针就是记录一下位置

			head.next = pre;
			head.last = next;
			pre = head;

			head = next;
		}
		return pre;
	}


    public static DoubleNode testReverseDoubleList(DoubleNode head) {
		if (head == null) {
			return null;
		}
		ArrayList<DoubleNode> list = new ArrayList<>();
		while (head != null) {
			list.add(head);
			head = head.next;
		}
		list.get(0).next = null;
		DoubleNode pre = list.get(0);
		int N = list.size();
		for (int i = 1; i < N; i++) {
			DoubleNode cur = list.get(i);
			cur.last = null;
			cur.next = pre;
			pre.last = cur;
			pre = cur;
		}
		return list.get(N - 1);
	}

全部代码见：Code01_ReverseList

package class03;

import java.util.ArrayList;
import java.util.List;

public class Code01_ReverseList {

	 public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            value = data;
        }
    }

    public static class DoubleNode {
        public int value;
        public DoubleNode last;
        public DoubleNode next;

        public DoubleNode(int data) {
            value = data;
        }
    }

    //  head
    //   a    ->   b    ->  c  ->  null
    //   c    ->   b    ->  a  ->  null
    public static Node reverseLinkedList(Node head) {
        Node pre = null;
        Node next = null;
        while (head != null) {
            next = head.next;	// next指针就是记录一下位置

            head.next = pre;
            pre = head;

            head = next;
        }
        return pre;
    }

    public static DoubleNode reverseDoubleList(DoubleNode head) {
        DoubleNode pre = null;
        DoubleNode next = null;
        while (head != null) {
            next = head.next;// next指针就是记录一下位置

            head.next = pre;
            head.last = next;
            pre = head;

            head = next;
        }
        return pre;
    }

    public static Node tesAreverseLinkedList(Node head) {
        if (head == null) {
            return null;
        }
        ArrayList<Node> list = new ArrayList<>();
        while (head != null) {
            list.add(head);
            head = head.next;
        }
        list.get(0).next = null;
        int N = list.size();
        for (int i = 1; i < N; i++) {
            list.get(i).next = list.get(i - 1);
        }
        return list.get(N - 1);
    }

    public static DoubleNode tesAreverseDoubleList(DoubleNode head) {
        if (head == null) {
            return null;
        }
        ArrayList<DoubleNode> list = new ArrayList<>();
        while (head != null) {
            list.add(head);
            head = head.next;
        }
        list.get(0).next = null;
        DoubleNode pre = list.get(0);
        int N = list.size();
        for (int i = 1; i < N; i++) {
            DoubleNode cur = list.get(i);
            cur.last = null;
            cur.next = pre;
            pre.last = cur;
            pre = cur;
        }
        return list.get(N - 1);
    }

    // for test
    public static Node generateRandomLinkedList(int len, int value) {
        int size = (int) (Math.random() * (len + 1));
        if (size == 0) {
            return null;
        }
        size--;
        Node head = new Node((int) (Math.random() * (value + 1)));
        Node pre = head;
        while (size != 0) {
            Node cur = new Node((int) (Math.random() * (value + 1)));
            pre.next = cur;
            pre = cur;
            size--;
        }
        return head;
    }

    // for test
    public static DoubleNode generateRandomDoubleList(int len, int value) {
        int size = (int) (Math.random() * (len + 1));
        if (size == 0) {
            return null;
        }
        size--;
        DoubleNode head = new DoubleNode((int) (Math.random() * (value + 1)));
        DoubleNode pre = head;
        while (size != 0) {
            DoubleNode cur = new DoubleNode((int) (Math.random() * (value + 1)));
            pre.next = cur;
            cur.last = pre;
            pre = cur;
            size--;
        }
        return head;
    }

    // for test
    public static List<Integer> getLinkedListOriginOrder(Node head) {
        List<Integer> ans = new ArrayList<>();
        while (head != null) {
            ans.add(head.value);
            head = head.next;
        }
        return ans;
    }

    // for test
    public static boolean checkLinkedLisAreverse(List<Integer> origin, Node head) {
        for (int i = origin.size() - 1; i >= 0; i--) {
            if (!origin.get(i).equals(head.value)) {
                return false;
            }
            head = head.next;
        }
        return true;
    }

    // for test
    public static List<Integer> getDoubleListOriginOrder(DoubleNode head) {
        List<Integer> ans = new ArrayList<>();
        while (head != null) {
            ans.add(head.value);
            head = head.next;
        }
        return ans;
    }

    // for test
    public static boolean checkDoubleLisAreverse(List<Integer> origin, DoubleNode head) {
        DoubleNode end = null;
        for (int i = origin.size() - 1; i >= 0; i--) {
            if (!origin.get(i).equals(head.value)) {
                return false;
            }
            end = head;
            head = head.next;
        }
        for (int i = 0; i < origin.size(); i++) {
            if (!origin.get(i).equals(end.value)) {
                return false;
            }
            end = end.last;
        }
        return true;
    }

    // for test
    public static void main(String[] args) {
        int len = 50;
        int value = 100;
        int testTime = 100000;
        System.out.println("test begin!");
        for (int i = 0; i < testTime; i++) {
            Node node1 = generateRandomLinkedList(len, value);
            List<Integer> list1 = getLinkedListOriginOrder(node1);
            node1 = reverseLinkedList(node1);
            if (!checkLinkedLisAreverse(list1, node1)) {
                System.out.println("Oops1!");
            }

            Node node2 = generateRandomLinkedList(len, value);
            List<Integer> list2 = getLinkedListOriginOrder(node2);
            node2 = tesAreverseLinkedList(node2);
            if (!checkLinkedLisAreverse(list2, node2)) {
                System.out.println("Oops2!");
            }

            DoubleNode node3 = generateRandomDoubleList(len, value);
            List<Integer> list3 = getDoubleListOriginOrder(node3);
            node3 = reverseDoubleList(node3);
            if (!checkDoubleLisAreverse(list3, node3)) {
                System.out.println("Oops3!");
            }

            DoubleNode node4 = generateRandomDoubleList(len, value);
            List<Integer> list4 = getDoubleListOriginOrder(node4);
            node4 = reverseDoubleList(node4);
            if (!checkDoubleLisAreverse(list4, node4)) {
                System.out.println("Oops4!");
            }

        }
        System.out.println("test finish!");

    }

}

（2）把给定值删除

举例：删除给定值3

注意：被删除的值可能会在头节点，所以方法返回要返回一个头节点。

代码如下：

package class03;

public class Code02_DeleteGivenValue {

	public static class Node {
		public int value;
		public Node next;

		public Node(int data) {
			this.value = data;
		}
	}

	// head = removeValue(head, 2);
	public static Node removeValue(Node head, int num) {
		// head来到第一个不需要删的位置
		while (head != null) {
			if (head.value != num) {
				break;
			}
			head = head.next;
		}
		// 1 ) head == null
		// 2 ) head != null
		Node pre = head;    // pre相当于上一个不等于3的位置
		Node cur = head;
		while (cur != null) {
			if (cur.value == num) {
				pre.next = cur.next;
			} else {
				pre = cur;
			}
			cur = cur.next;
		}
		return head;
	}

}

Java和C++在内存释放上的问题：
问：Java代码会不会产生内存泄露。
答：会。

4.栈和队列

（1）逻辑概念

栈：数据先进后出，犹如弹夹。
队列：数据先进先出，好似排队。

（2）栈和队列的实际实现

双向链表实现栈和队列：

代码如下：

package class03;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class Code03_DoubleEndsQueueToStackAndQueue {

	public static class Node<T> {
		public T value;
		public Node<T> last;
		public Node<T> next;

		public Node(T data) {
			value = data;
		}
	}

	public static class DoubleEndsQueue<T> {
		public Node<T> head;
		public Node<T> tail;

		public void addFromHead(T value) {
			Node<T> cur = new Node<T>(value);
			if (head == null) {
				head = cur;
				tail = cur;
			} else {
				cur.next = head;
				head.last = cur;
				head = cur;
			}
		}

		public void addFromBottom(T value) {
			Node<T> cur = new Node<T>(value);
			if (head == null) {
				head = cur;
				tail = cur;
			} else {
				cur.last = tail;
				tail.next = cur;
				tail = cur;
			}
		}

		public T popFromHead() {
			if (head == null) {
				return null;
			}
			Node<T> cur = head;
			if (head == tail) {
				head = null;
				tail = null;
			} else {
				head = head.next;
				cur.next = null;
				head.last = null;
			}
			return cur.value;
		}

		public T popFromBottom() {
			if (head == null) {
				return null;
			}
			Node<T> cur = tail;
			if (head == tail) {
				head = null;
				tail = null;
			} else {
				tail = tail.last;
				tail.next = null;
				cur.last = null;
			}
			return cur.value;
		}

		public boolean isEmpty() {
			return head == null;
		}

	}

	// 栈
	public static class MyStack<T> {
		private DoubleEndsQueue<T> queue;

		public MyStack() {
			queue = new DoubleEndsQueue<T>();
		}

		public void push(T value) {
			queue.addFromHead(value);
		}

		public T pop() {
			return queue.popFromHead();
		}

		public boolean isEmpty() {
			return queue.isEmpty();
		}

	}

	// 队列
	public static class MyQueue<T> {
		private DoubleEndsQueue<T> queue;

		public MyQueue() {
			queue = new DoubleEndsQueue<T>();
		}

		public void push(T value) {
			queue.addFromHead(value);
		}

		public T poll() {
			return queue.popFromBottom();
		}

		public boolean isEmpty() {
			return queue.isEmpty();
		}

	}

	public static boolean isEqual(Integer o1, Integer o2) {
		if (o1 == null && o2 != null) {
			return false;
		}
		if (o1 != null && o2 == null) {
			return false;
		}
		if (o1 == null && o2 == null) {
			return true;
		}
		return o1.equals(o2);
	}

	public static void main(String[] args) {
		int oneTestDataNum = 100;
		int value = 10000;
		int testTimes = 100000;
		for (int i = 0; i < testTimes; i++) {
			MyStack<Integer> myStack = new MyStack<>();
			MyQueue<Integer> myQueue = new MyQueue<>();
			Stack<Integer> stack = new Stack<>();
			Queue<Integer> queue = new LinkedList<>();
			for (int j = 0; j < oneTestDataNum; j++) {
				int nums = (int) (Math.random() * value);
				if (stack.isEmpty()) {
					myStack.push(nums);
					stack.push(nums);
				} else {
					if (Math.random() < 0.5) {
						myStack.push(nums);
						stack.push(nums);
					} else {
						if (!isEqual(myStack.pop(), stack.pop())) {
							System.out.println("oops!");
						}
					}
				}
				int numq = (int) (Math.random() * value);
				if (stack.isEmpty()) {
					myQueue.push(numq);
					queue.offer(numq);
				} else {
					if (Math.random() < 0.5) {
						myQueue.push(numq);
						queue.offer(numq);
					} else {
						if (!isEqual(myQueue.poll(), queue.poll())) {
							System.out.println("oops!");
						}
					}
				}
			}
		}
		System.out.println("finish!");
	}

}

数组实现栈和队列：

数组实现栈：数组大小为7。

正常使用，代码省略。

 public static class MyStack {

        private int[] arr;
        private int top;  // 栈底，初始化为-1
        private final int limit;

        public MyStack(int limit) {
            arr = new int[limit];
            top = 0;
            this.limit = limit;
        }

        // 放元素
        private void push(int value) {
            if (top == limit - 1) {
                throw new RuntimeException("队列满了，不能再加了");
            }
            top++;
            arr[top] = value;
        }

        // 取元素
        public int pop() {
            if (top == -1) {
                throw new RuntimeException("队列空了，不能再拿了");
            }
            int ans = arr[top];
            top--;
            return ans;
        }

        public boolean isEmpty() {
            return top == -1;
        }

    }

数组实现队列：数组大小为7，考虑一个机制使能循环使用数组空间–RingBuffer，putIndex放入元素，pollIndex拿元素。环形数组。

代码如下：

package class03;

public class Code04_RingArray {

	public static class MyQueue {
		private int[] arr;
		private int pushi;// end
		private int polli;// begin
		private int size;
		private final int limit;

		public MyQueue(int limit) {
			arr = new int[limit];
			pushi = 0;
			polli = 0;
			size = 0;
			this.limit = limit;
		}

		public void push(int value) {
			if (size == limit) {
				throw new RuntimeException("队列满了，不能再加了");
			}
			size++;
			arr[pushi] = value;
			pushi = nextIndex(pushi);
		}

		public int pop() {
			if (size == 0) {
				throw new RuntimeException("队列空了，不能再拿了");
			}
			size--;
			int ans = arr[polli];
			polli = nextIndex(polli);
			return ans;
		}

		public boolean isEmpty() {
			return size == 0;
		}

		// 如果现在的下标是i，返回下一个位置
		private int nextIndex(int i) {
			return i < limit - 1 ? i + 1 : 0;
		}

	}

}

5.既然语言都有这些结构和api，为什么还需要手撸练习

（1）算法问题无关语言
（2）语言提供的api是有限的，当有新的功能是api不提供的，就需要改写
（3）任何软件工具的底层都是最基本的算法和数据结构，这是绕不过去的。

举例：LRU算法（需要用到哈希表），此处暂省。

6.栈和队列的常见面试题

（1）题目一：怎么用数组实现不超过固定大小的队列和栈？

栈：正常使用
队列：环形数组

解法：见第4点的第（2）点。

（2）题目二：实现一个特殊的栈，在基本功能的基础上，再实现返回栈中最小元素的功能。

（1）pop、push、 getmin操作的时间复杂度都是O(1)。
（2）设计的栈类型可以使用现成的栈结构。

解法1：

第一种设计，准备两个栈，Data栈存放栈的数据，每加一个新数据到Data中，min栈中新加一个数据为Data栈目前所有被添加数据中的最小值。


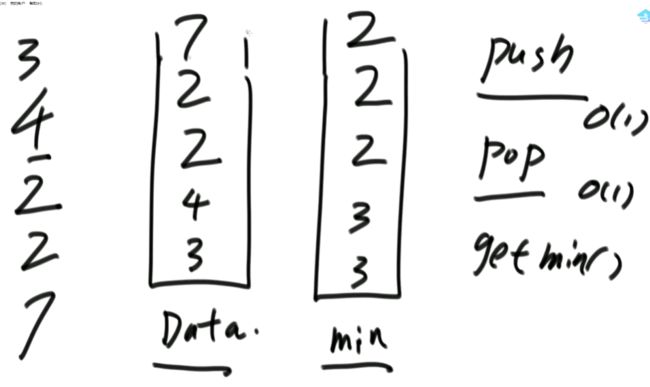
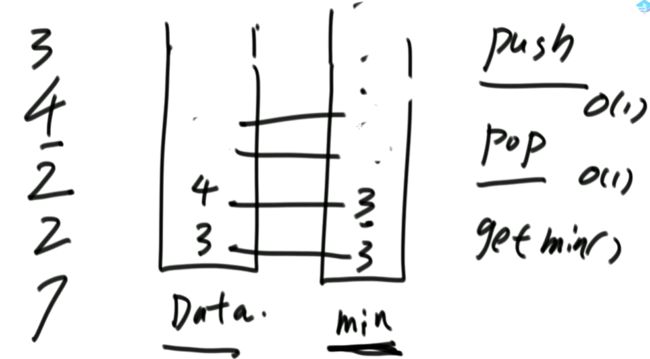
min栈存的数据是Data栈每一个level情况下的最小值。

代码如下：

public static class MyStack2 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack2() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum < this.getmin()) {
				this.stackMin.push(newNum);
			} else {
				int newMin = this.stackMin.peek();
				this.stackMin.push(newMin);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			this.stackMin.pop();
			return this.stackData.pop();
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

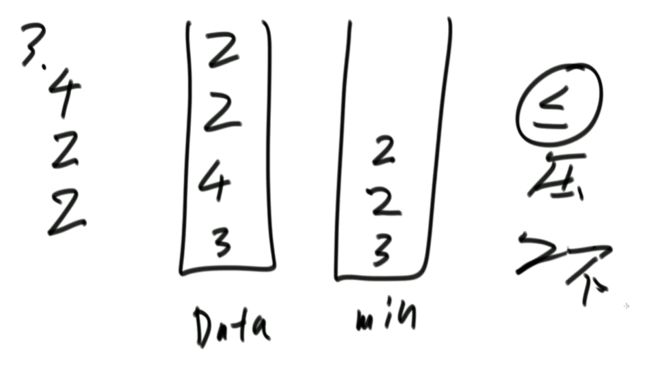
解法2：

第二种设计，准备两个栈，Data栈存放栈的数据，每加一个新数据到Data中，比较Data栈刚加入的数据a和前一个添加的数据b的大小。如果刚加入的数据a小于等于前一个添加的数据b，那么把刚加入的数据a也添加到min栈中；如果刚加入的数据a大于前一个添加的数据b，则不添加。取数据的时候，若Data栈的栈顶数据与min栈栈顶数据相等，弹出Data栈的栈顶数据和min栈栈顶数据。若Data栈的栈顶数据与min栈栈顶数据不相等，弹出Data栈的栈顶数据。

实现方法简单，代码如下：

public static class MyStack1 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack1() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum <= this.getmin()) {
				this.stackMin.push(newNum);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			int value = this.stackData.pop();
			if (value == this.getmin()) {
				this.stackMin.pop();
			}
			return value;
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

全部代码如下：

 package class03;

import java.util.Stack;

public class Code05_GetMinStack {

	public static class MyStack1 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack1() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum <= this.getmin()) {
				this.stackMin.push(newNum);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			int value = this.stackData.pop();
			if (value == this.getmin()) {
				this.stackMin.pop();
			}
			return value;
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

	public static class MyStack2 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack2() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum < this.getmin()) {
				this.stackMin.push(newNum);
			} else {
				int newMin = this.stackMin.peek();
				this.stackMin.push(newMin);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			this.stackMin.pop();
			return this.stackData.pop();
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

	public static void main(SAring[] args) {
		MyStack1 stack1 = new MyStack1();
		stack1.push(3);
		System.out.println(stack1.getmin());
		stack1.push(4);
		System.out.println(stack1.getmin());
		stack1.push(1);
		System.out.println(stack1.getmin());
		System.out.println(stack1.pop());
		System.out.println(stack1.getmin());

		System.out.println("=============");

		MyStack1 stack2 = new MyStack1();
		stack2.push(3);
		System.out.println(stack2.getmin());
		stack2.push(4);
		System.out.println(stack2.getmin());
		stack2.push(1);
		System.out.println(stack2.getmin());
		System.out.println(stack2.pop());
		System.out.println(stack2.getmin());
	}

}

比较：

第一种方法稍微费一点空间，弹数据的时候不用判断，省一点时间。第二种方法省一点空间，但是压入和弹出数据都要判断，时间要多一点。

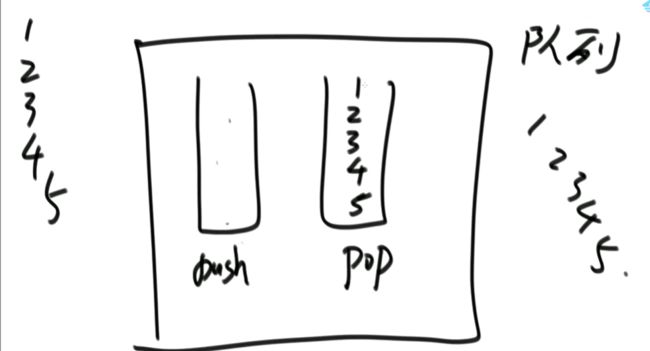
（3）如何用栈结构实现队列结构

解法：创建两个栈，push栈和pop栈。加入数据1，2，3，4，5到push栈。pop栈为空的情况下把push栈数据添加到pop栈中，此时我们取数据从pop中取，第一个被取的就是1了。如果取了数字1后又添加数据6到队列了，那么push栈中添加数据6。取数据依然从pop栈中取。pop栈中取完了，push栈数据导入pop栈，继续取。

注意：push栈数据导入pop栈，坚持两个原则。其一，一旦导入数据要依次导完；其二，必须是在pop栈为空的情况下。

代码如下：

package class03;

import java.util.Stack;

public class Code06_TwoStacksImplementQueue {

	public static class TwoStacksQueue {
		public Stack<Integer> stackPush;
		public Stack<Integer> stackPop;

		public TwoStacksQueue() {
			stackPush = new Stack<Integer>();
			stackPop = new Stack<Integer>();
		}

		// push栈向pop栈倒入数据
		private void pushToPop() {
			if (stackPop.empty()) {
				while (!stackPush.empty()) {
					stackPop.push(stackPush.pop());
				}
			}
		}

		public void add(int pushInt) {
			stackPush.push(pushInt);
			pushToPop();
		}

		public int poll() {
			if (stackPop.empty() && stackPush.empty()) {
				throw new RuntimeException("Queue is empty!");
			}
			pushToPop();
			return stackPop.pop();
		}

		public int peek() {
			if (stackPop.empty() && stackPush.empty()) {
				throw new RuntimeException("Queue is empty!");
			}
			pushToPop();
			return stackPop.peek();
		}
	}

	public static void main(String[] args) {
		TwoStacksQueue test = new TwoStacksQueue();
		test.add(1);
		test.add(2);
		test.add(3);
		System.out.println(test.peek());
		System.out.println(test.poll());
		System.out.println(test.peek());
		System.out.println(test.poll());
		System.out.println(test.peek());
		System.out.println(test.poll());
	}

}

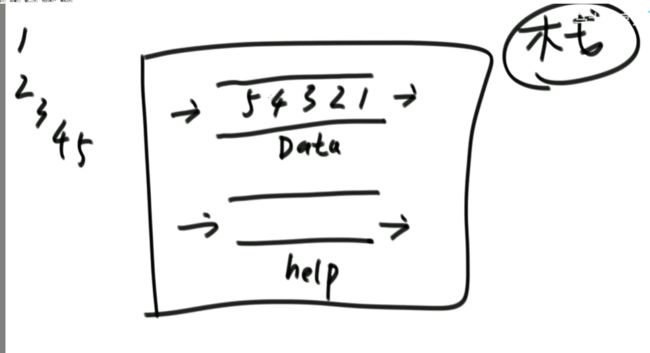
（4）如何用队列结构实现栈结构

解法：创建两个队列。原始队列Data，辅助队列help。假设Data加入数据1,2,3,4,5。弹出数据要弹为：5，4，3，2，1。第一个弹出的要是5。我们可以把1，2，3，4加入到help栈中，5留在Data栈中。之后help变为Data，Data变为help。那么此时我们弹出的第一个数据就是5了。

代码如下：

package class03;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class Code07_TwoQueueImplementStack {

	public static class TwoQueueStack<T> {
		public Queue<T> queue;
		public Queue<T> help;

		public TwoQueueStack() {
			queue = new LinkedList<>();
			help = new LinkedList<>();
		}

		public void push(T value) {
			queue.offer(value);
		}

		public T poll() {
			while (queue.size() > 1) {
				help.offer(queue.poll());
			}
			T ans = queue.poll();
			Queue<T> tmp = queue;
			queue = help;
			help = tmp;
			return ans;
		}

		public T peek() {
			while (queue.size() > 1) {
				help.offer(queue.poll());
			}
			T ans = queue.poll();
			help.offer(ans);
			Queue<T> tmp = queue;
			queue = help;
			help = tmp;
			return ans;
		}

		public boolean isEmpty() {
			return queue.isEmpty();
		}

	}

	public static void main(String[] args) {
		System.out.println("test begin");
		TwoQueueStack<Integer> myStack = new TwoQueueStack<>();
		Stack<Integer> test = new Stack<>();
		int testTime = 1000000;
		int max = 1000000;
		for (int i = 0; i < testTime; i++) {
			if (myStack.isEmpty()) {
				if (!test.isEmpty()) {
					System.out.println("Oops");
				}
				int num = (int) (Math.random() * max);
				myStack.push(num);
				test.push(num);
			} else {
				if (Math.random() < 0.25) {
					int num = (int) (Math.random() * max);
					myStack.push(num);
					test.push(num);
				} else if (Math.random() < 0.5) {
					if (!myStack.peek().equals(test.peek())) {
						System.out.println("Oops");
					}
				} else if (Math.random() < 0.75) {
					if (!myStack.poll().equals(test.pop())) {
						System.out.println("Oops");
					}
				} else {
					if (myStack.isEmpty() != test.isEmpty()) {
						System.out.println("Oops");
					}
				}
			}
		}

		System.out.println("test finish!");

	}

}

图的宽度优先遍历，是用队列实现的。

图的深度优先遍历，是用栈实现的。

面试问题：
问：我可以用栈实现图的宽度优先遍历。队列实现图的深度优先遍历。是怎么实现的？
答：套壳就行了，方法见（3）（4）

7.递归？这东西是什么？

怎么试代码

怎么从思想上理解递归；
怎么从实际实现的角度出发理解递归。

举例：

求数组arr[L…R]中的最大值，怎么用递归方法实现。
（1）将[L…R]范围分成左右两半。左：[L…Mid] 右：[Mid+1…R]
（2）左部分求最大值，右部分求最大值。
（3）[L…R]范围上的最大值，是max{左部分最大值,右部分最大值}

注意：（2）是个递归过程,当范围上只有一个数，就可以不用再递归了。

解法：

代码如下：

package class03;

public class Code08_GetMax {

	// 求arr中的最大值
	public static int getMax(int[] arr) {
		return process(arr, 0, arr.length - 1);
	}

	// arr[L..R]范围上求最大值  L ... R   N
	public static int process(int[] arr, int L, int R) {
		// arr[L..R]范围上只有一个数，直接返回，base case
		if (L == R) { 
			return arr[L];
		}
		// L...R 不只一个数
		// mid = (L + R) / 2
		int mid = L + ((R - L) >> 1); // 中点   	1
		int leftMax = process(arr, L, mid);
		int rightMax = process(arr, mid + 1, R);
		return Math.max(leftMax, rightMax);
	}

}

时间复杂度：O(N)

递归利用的是系统栈，若递归过大会出现栈溢出错误。

任何递归行为都能改成非递归行为，我们不使用系统栈即可，就可以把递归改为迭代。

有些语言的尾递归是发现了这个递归行为后自己优化了一下，使递归在实际运行时已经成为了迭代。迭代就是用for循环，while，do…while。

问：对于某一类递归行为的时间复杂度是确定的，哪一类？

答：子问题的规模是一致的，且变为更小的规模，即b>1。a为子递归调用了a次。除去子问题对于之外的时间复杂度为O(N ^ d)

对于上面的怎么试代码的举例，有leftMax和rightMax，所以调用了两次，a=2，子问题的规模是1/2，b=2. O(N ^ d)为除了递归部分之外的时间复杂度，上方的举例为O(N ^ 0)

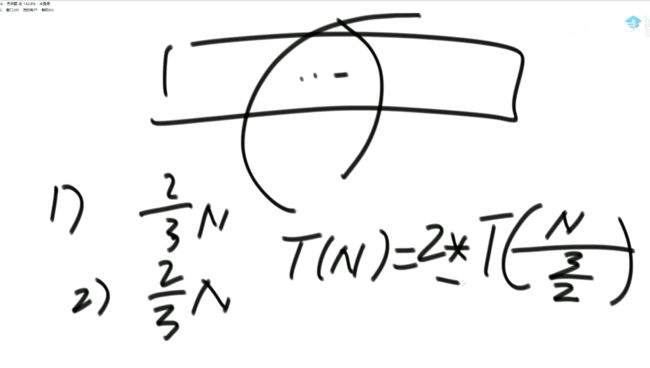
再举一个例子解释这个公式：

一个数组分成两份递归，前2/3，后2/3分别递归。

则b=3/2。左侧2/3，右侧2/3，调用了2次，所以a=2。除了递归的部分，其他的时间复杂度为O(N ^ 0)。

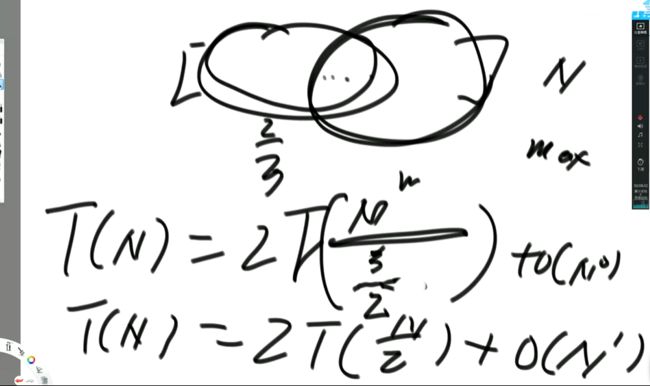
进一步总结：

如果一个递归行为公式满足：

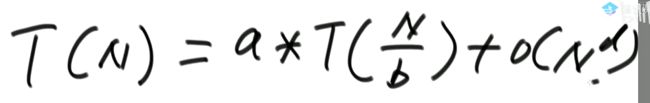
时间复杂度有下列情形：

即：形如
T(N) = a * T(N / b) + O(N ^ d)（其中的a、b、d都是常数）
的递归函数，可以直接通过 Master公式来确定时间复杂度
如果log(b,a) 如果log(b,a)>d，复杂度为O(N ^ log(b,a) )
如果log(b,a)==d，复杂度为O( (N ^ d)*logN)

举例1：

还是上方的怎么试代码的举例，有leftMax和rightMax，所以调用了两次，a=2，子问题的规模是1/2，b=2. O(N ^ d)为除了递归的时间复杂度，上方的举例为O(N的0次方)。所以d=0

log以b为底的a的对数=1>d 所以O(1)。这也验证了时间复杂度的第一个情形。

举例2：

下方为a!=b的时候：前2/3，后2/3调用了2次。a=2,b=3/2 。

8.哈希表

（1）哈希表在使用层面上可以理解为一种集合结构
（2）如果只有key，没有伴随数据 value，可以使用 Hashset结构
（3）如果既有key，又有伴随数据 value，可以使用 Hashmap结构
（4）有无伴随数据，是 Hashmap和hashset唯一的区别，实际结构是一回事
（5）使用哈希表增(put)、删(remove)、改(put)和查(get)的操作，可以认为时间复杂度为O(1)，但是常数时间比较大。
（6）放入哈希表的东西，如果是基础类型，内部按值传递，内存占用是这个东西的大小。
（7）放入哈希表的东西，如果不是基础类型，内部按引用传递，内存占用是8字节。

Java的哈希表包括：Hashmap,Hashset,Hashtable。

哈希表的一些基础使用如下：

  // c++中HashMap叫做UnSortedMap
        // HashMap为键值对
		HashMap<Integer, String> map = new HashMap<>();
		map.put(1000000, "我是1000000");
		// put()为新增和修改
		map.put(2, "我是2");
		map.put(3, "我是3");
		map.put(4, "我是4");
		map.put(5, "我是5");
		map.put(6, "我是6");
		map.put(1000000, "我是1000001");

		// 查询是否包含
		System.out.println(map.containsKey(1));
		System.out.println(map.containsKey(10));

		// 获取值。有则返回，无返回null。
		System.out.println(map.get(4));
		System.out.println(map.get(10));

		map.put(4, "他是4");
		System.out.println(map.get(4));

		// 删除某个值
		map.remove(4);
		System.out.println(map.get(4));

		// HashSet只有键
		HashSet<String> set = new HashSet<>();

		// 新增
		set.add("abc");
		// 查询是否包含
		set.contains("abc");
		// 删除
		set.remove("abc");

		// 哈希表，增、删、改、查，在使用时所有的api时间复杂度都是O（1）

哈希表里无论是基本数据类型还是包装数据类型，对于key一律按值传递。但是如果是自己定义的数据类型，就是按引用传递！

举例：下方输出结果为1

HashMap<Node, String> map2 = new HashMap<>();
		Node node1 = new Node(1);
		Node node2 = node1;
		map2.put(node1, "我是node1");
		map2.put(node2, "我是node1");
		System.out.println(map2.size());

举例：下方输出结果为2

 		HashMap<Node, String> map2 = new HashMap<>();
		Node node1 = new Node(1);
		Node node2 = new Node(2);
		map2.put(node1, "我是node1");
		map2.put(node2, "我是node1");
		System.out.println(map2.size());

关于equals和==还是别参看这里了，有些问题。

int,double,float等基本数据类型是按值传递的。基本数据类型使用只可以使用==。

Integer,Double,Float等包装数据类型在它们的范围外是按引用传递的，范围内是按值传递的。包装数据类型使用==且超过范围是比较它们的内存地址，没超过范围也比较值，。equals()是比较它们的值。

这一段有空需要润色一下，比较内存地址，equals()方法比较值。两个变量按值传递且用比较那么返回true。两个变量按引用传递且用==比较那么返回false。两个变量无论按值传递好事按引用传递使用equals()方法都返回true。

1、“==”比较两个变量本身的值，即两个对象在内存中的首地址。

2、“equals()”比较字符串中所包含的内容是否相同。

举例1：下方返回true,==且为基本数据类型，比较值。虽然c,d的内存区域不同，而值相同。

    	int c = 100000;
		int d = 100000;
		System.out.println(c == d);

举例2： 下方返回true，equals()方法就是比较值

  		Integer c = 100000;
		Integer d = 100000;
		System.out.println(c.equals(d));

举例3： 下方返回false，==且为包装数据类型比较内存地址

   		Integer c = 100000;
		Integer d = 100000;
		System.out.println(c == d);

举例4：下方都返回true。包装数据类型使用==但没超过它们的范围还是按值传递，比较值。

    	Integer e = 7; // - 128 ~ 127
		Integer f = 7;
		System.out.println(e == f);
        Integer e = 127; // - 128 ~ 127
		Integer f = 127;
		System.out.println(e == f);

对于一个Hash，使用map的put()方法加了四次相同的记录到map中。那么map的容量为4倍的记录。按值传递是还要复制3份相同的。String也是按引用的，但是在hash里，基本数据类型和包装数据类型都是按值传递的，只有自己定义的数据类型是按引用传递的

对于一个Hash，Node为自己定义的数据类型。使用map的put()方法加了四次相同的记录到map中。那么map的容量为1份记录和3份引用。其容量是比上方小的。

9.有序表

Java中哈希表是HashMap，而c++中叫做UnSortedMap。Java中有序表是TreeMap

		// TreeMap 有序表：接口名
		// 红黑树、avl、sb树、跳表
		// O(logN)
		System.out.println("有序表测试开始");
		TreeMap<Integer, String> treeMap = new TreeMap<>();

		treeMap.put(3, "我是3");
		treeMap.put(4, "我是4");
		treeMap.put(8, "我是8");
		treeMap.put(5, "我是5");
		treeMap.put(7, "我是7");
		treeMap.put(1, "我是1");
		treeMap.put(2, "我是2");

		System.out.println(treeMap.containsKey(1));
		System.out.println(treeMap.containsKey(10));

		System.out.println(treeMap.get(4));
		System.out.println(treeMap.get(10));

		treeMap.put(4, "他是4");
		System.out.println(treeMap.get(4));

//		treeMap.remove(4);
		System.out.println(treeMap.get(4));

		System.out.println("新鲜：");

		System.out.println(treeMap.firstKey());
		System.out.println(treeMap.lastKey());

		// <= 4
		System.out.println(treeMap.floorKey(4));
		// >= 4
		System.out.println(treeMap.ceilingKey(4));
		// 上述所有接口的时间按复杂度都是O(logN)

有序表对基本数据类型它自带了比较方法。而自定义数据类型怎么办我们会在堆中再谈有序表。

有序表底层有多种实现：AVL,SB,红黑树，跳表。前三者是具有不同平衡性的搜索二叉树。

大量产品功能的实现都不用红黑树实现了。

三、归并排序与随机快排

归并排序既用了递归方法也用了非递归方法

1.归并排序

（1）整体是递归,左边排好序+右边排好序+merge让整体有序
（2）让其整体有序的过程里用了排外序方法
（3）利用master公式来求解时间复杂度
（4）当然可以用非递归实现

举例：假设一个无序数组arr[5，3，2，5，6，0]

根据归并排序，把arr[]分成两部分，[5,3,2]和[5,6,0]
把左边的排好序[2,3,5]，右边的也排好序[0,5,6]。之后把整体再排序，

整体排序方法：
准备一个与arr[]大小相等的数组。左数组与右数组比较第一个，小的先放入新数组的第一个位置，大的再参与比较，之后再比较左右数组的中第i-1个中的大的元素和第i个中的小的元素，依此类推。新数组整体有序后再复制回到arr[]数组中。

代码如下（其中包含了递归和非递归）：

package class04;

public class Code01_MergeSort {

	// 递归方法实现
	public static void mergeSort1(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		process(arr, 0, arr.length - 1);
	}

	// 请把arr[L..R]排有序
	// l...r N
	// T(N) = 2 * T(N / 2) + O(N)
	// O(N * logN)
	public static void process(int[] arr, int L, int R) {
		if (L == R) { // base case
			return;
		}
		int mid = L + ((R - L) >> 1);
		process(arr, L, mid);
		process(arr, mid + 1, R);
		merge(arr, L, mid, R);
	}

	public static void merge(int[] arr, int L, int M, int R) {
		int[] help = new int[R - L + 1];	// 或许也可以写成arr.size()
		int i = 0;
		// 左数组的第一个位置
		int p1 = L;
		// 右数组的第一个位置
		int p2 = M + 1;
		// 限定p1和p2不越界
		while (p1 <= M && p2 <= R) {
			// 比较左数组和右数组的第i个元素，判断大小，小的先放进新数组，大的再比较。相等则下放进左数组的。
			help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
		}
		// 要么p1越界了，要么p2越界了
		while (p1 <= M) {
			help[i++] = arr[p1++];
		}
		while (p2 <= R) {
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {
			arr[L + i] = help[i];
		}
	}

	// 非递归方法实现
	public static void mergeSort2(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int N = arr.length;
		// 步长
		int mergeSize = 1;
		while (mergeSize < N) { // log N
			// 当前左组的，第一个位置
			int L = 0;
			while (L < N) {
				if (mergeSize >= N - L) {
					break;
				}
				int M = L + mergeSize - 1;
				int R = M + Math.min(mergeSize, N - M - 1);
				merge(arr, L, M, R);
				L = R + 1;
			}
			// 防止溢出
			if (mergeSize > N / 2) {
				break;
			}
			mergeSize <<= 1;
		}
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		System.out.println("测试开始");
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			mergeSort1(arr1);
			mergeSort2(arr2);
			if (!isEqual(arr1, arr2)) {
				System.out.println("出错了！");
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println("测试结束");
	}

}

对于非递归的解析：
int mergeSize = 1;为第1个数为左部分，下1个数为右部分。第3个数为左部分，第4个数为右部分，依此类推。
mergeSize <<= 1;为规模乘以2.把前2个数作为左部分，下两个数为右部分。
如果左部分或右部分的数量不够规模，那有多少就多少。
直到所有数都为左部分。

关于时间复杂度：

	归并排序的递归与非递归方法的时间复杂度都是O(N*log(N))。
	选择、冒泡、插入排序的时间复杂度是O(N ^ 2)，这三者排序浪费了大量的比较行为，因此其时间复杂度高。

2.用常见面试题再深入理解一下归并排序的精髓

题目：在一个数组中，一个数左边比它小的数的总和，叫数的小和，所有数的小和累加起来，叫数组小和。求数组小和。
例子：[1.3,4,2.5]
1左边比1小的数：没有
3左边比3小的数：1
4左边比4小的数：1、3
2左边比2小的数：1
5左边比5小的数：1、3、4、2
所以数组的小和为1+1+3+1+1+3+4+2=16

解析：即求右边有多少个数比他大，左组指针不断向右调。

可以用暴力递归，每个人都遍历找一下左边比他小的数（不推荐）
利用归并排序来解决这个问题（推荐）。

解法：利用归并排序来解决这个问题。

左组比右组小的时候产生小和；左组的数与右组的数相等的时候，先拷贝右组的数，不产生小和；右组的数小于左组的数的时候先拷贝右组的数，不产生小和。

arr[1,3,4,2,5]。1，3划为左侧数组。4，2，5划为右侧数组。

看左组的1，3.再划分。1为左组，3为右组，左组比右组小产生小和，此时右组上只有一个数比1大，产生一个1.把1，3拷贝一下到help数组中再粘贴回去到左组。左组只产生了1这个小和。

看右组的4，2，5.再划分。4为左组，2，5为右组。再划分，4没的划，暂放。然后2划为左组，5划为右组。左组比右组小产生小和。此时右组上只有一个数比1大，产生一个2.把2，5拷贝一下到help数组中再粘贴回去到2，5的右组。

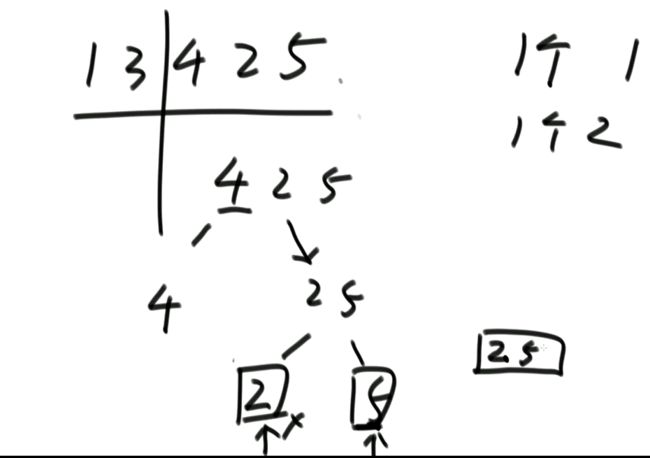
上面已经把第四层，2为左组，5为右组的给解决了。我们接下来看第三层。 4为左组，2，5为右组的。2<4，2先拷贝到help数组中，且不产生小和；4<5，左组数小于右组数，右组上只有1个数5比4大，产生1个4.接下来再把4，5拷贝到help数组中。同时再把help数组的[2,4,5]粘贴到上面的4,2,5中。

之后我们又回到了第一层，[1,3]为左组，[2,4,5]为右组。接下来合并第一层。左组第一个数与右组每个数比较，1<2，又这是排好序的，所以右组有3个数比左组的1大，小和产生3个1.同时再把1拷贝到help数组中。左组指针再到第二个数3，3和右组第一个数2比较，3>2，左组大于右组，不产生小和，先把右组的数拷贝进help数组中。3再和右组的4比较。3<4，左组小于右组，产生小和，右组有两个数比3大，小和中产生2个3.再把3拷贝进help数组，4，5拷贝进help数组。此时help数组：[1,2,3,4,5]。再把help数组赋值给arr数组。

[1,3,4,2,5]这个数组求小和的另一种理解：1右边有4个数比1大，3右边有2个数比3大，4右边有1个数比4大，2右边有1个数比2大，5右边有0个数比5大。即有4个1，2个3，1个4，1个2，0个5.

小和产生的时候就是merge的时候。每一次merge的时候会产生小和。再举例：一个数组。第一层左组：[1,2,2,3,3]，右组：[2,2,3,34]。左组第一个数1和右组第一个数2比较.1<2。左组小于右组，产生小和，右组有5个数比左组的当前数1大，所以产生5个1，同时1拷贝进help数组。左组第2个数2与右组第2个数2比较，相等，不产生小和，先拷贝右组数到help数组.左组第2个数2与右组第2个数2比较，相等，不产生小和，先拷贝右组数到help数组，此时help[1,2,2]。左组第2个数2与右组第3个数3比较.左组小于右组，产生小和。右组有3个数比左组当前数大，产生3个2.依此类推…

[1,3,4,2,5]求小和的代码如下：

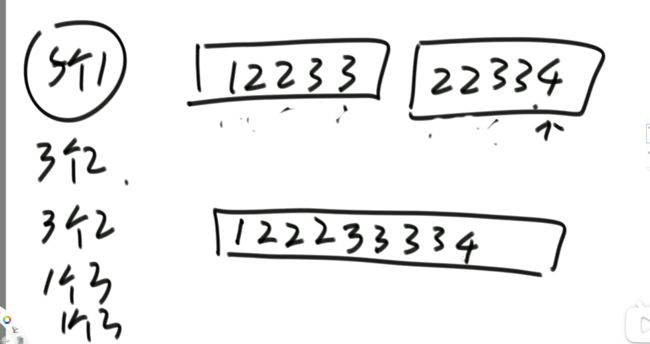
package class04;

public class Code02_SmallSum {

	public static int smallSum(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		return process(arr, 0, arr.length - 1);
	}

	// arr[L..R]既要排好序，也要求小和返回
	// 所有merge时，产生的小和，累加
	// 第一层左组 排序，下又再分左右组  有若干merge行为
	// 第一层右组 排序，下又再分左右组  有若干merge行为
	// 第一层排号序后，整个merge行为
	public static int process(int[] arr, int l, int r) {
		if (l == r) {
			return 0;
		}
		// l < r
		int mid = l + ((r - l) >> 1);
		return 
                // 左侧所有merge行为返回一个小和

				process(arr, l, mid) 
				+ 
                // 右侧所有merge行为返回一个小和

				process(arr, mid + 1, r) 
				+ 
                // 左右两组排好序后整体merge行为返回一个小和
                
				merge(arr, l, mid, r);
	}

	public static int merge(int[] arr, int L, int m, int r) {
		int[] help = new int[r - L + 1];
		int i = 0;
		int p1 = L;
		int p2 = m + 1;
		int res = 0;
		while (p1 <= m && p2 <= r) {
			res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
			help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
		}
		while (p1 <= m) {
			help[i++] = arr[p1++];
		}
		while (p2 <= r) {
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {
			arr[L + i] = help[i];
		}
		return res;
	}

	// for test
	public static int comparator(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int res = 0;
		for (int i = 1; i < arr.length; i++) {
			for (int j = 0; j < i; j++) {
				res += arr[j] < arr[i] ? arr[j] : 0;
			}
		}
		return res;
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			if (smallSum(arr1) != comparator(arr2)) {
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

总结：数组中左或右边有多少个数比当前数小或大就可以使用mergeSort。

另一相似例题1：求[3,1,7,0,2]的降序对（逆序对）。降序对（逆序对）：(3,1),(3,0),(3,2),(1,0),(7,0),(7,2) 即逆序对(x,y)要满足x>y且x出现在y前面，左组小于右组的时候会产生被要求求的。即求一个数左边有多少个数比他大。

另一相似例题2：数组的左组[1,1,2,2,3]，右组[1，1，1，4,4,4]。求一个数左边有多少个数比他大。左组右组相等，先拷贝左边的数。左组小于右组的时候会产生被要求求的。右组指针不断向右调

3.快速排序

Partition：分层，分区。

Partition过程

给定一个数组arr，和一个整数num。请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。
要求额外空间复杂度O(1),时间复杂度O(N)

补充：放在数组左边的数不要求有序，放在数组右边的数不要求有序。

解法：

创建一个区域”<=区“用于存储小于等于的数，放在数组arr的左面（<=区最初在数组的-1位置）。遍历arr数组，[i]就是遍历数组的指针。

若arr[i]<=num，arr[i]和”<=区“的下一个数(下标为0的位置)交换，”<=区“右扩一个位置（下次的<=区的下一个书就是下标为1的位置），然后i++。

若arr[i]>num，i++。

升级—荷兰国旗问题：

给定一个数组arr，数组中给你一个整数num。要求小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边，左边和右边的数可以无序。要求额外空间复杂度O(1)，时间复杂度O(N)。这也就是经典的荷兰国旗问题，三色。

对于上述升级的举例：

num的数在右边。

解法：

<区向右扩，>区向左扩。

如果arr[i] == num，i++

如果arr[i] < num ，arr[i]与<区右一个位置交换;<区右扩;i++（与上同）

如果arr[i] > num ，arr[i]与>区左一个位置交换;>区左扩;i不动

遍历arr数组，当到第一个数3的时候，3<4，3与<区的右一个位置也就是自己交换，<区右扩，i++

当i++后，i=2，arr[2]=5，6与>区的左一个位置也就是2交换，>区左扩，i不动

i不动，所以此时arr[2] = 2。继续比较 2<4，所以…如下图

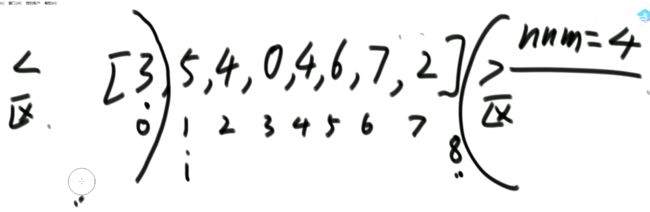
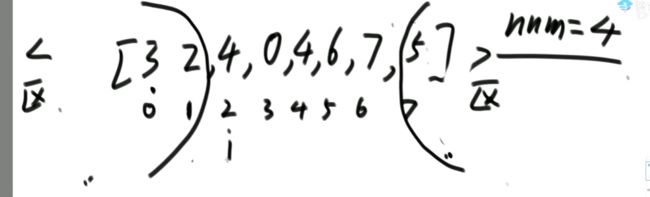
回归到快速排序：

快速排序1.0

在arr[L…R]范围上，进行快速排序的过程：我们这里是吧arr[R]当作上面所说的num，也即其他说法的pivot，pivot也可以选定为其他数。
（1）用arr[R]对该范围做partition，<=arr[R]的数在左部分并且保证arr[R]最后来到左部分的最后一个位置，记为M；>arr[R]的数在右部分 (arr[M+1…R])
（2）对arr[L…M-1]进行快速排序（递归）
（3）对arr[M+1…R]进行快速排序（递归）
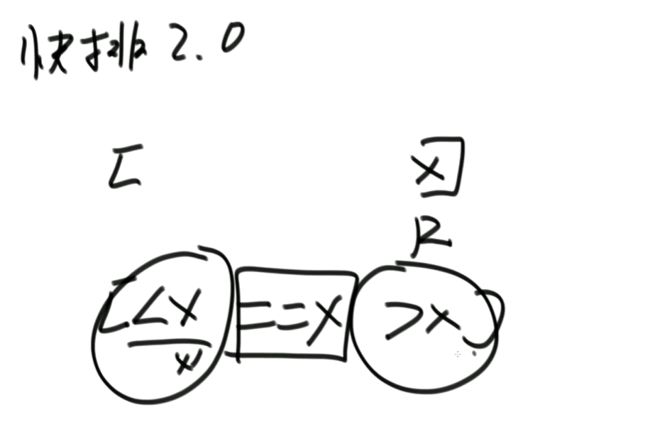
因为每一次 partition都会搞定一个数的位置且不会再变动，所以排序能完成。

算法核心是partition方法，即把元素分开两组的方法，每次把元素平均分到两边时，算法效率最高。相反，如果每次partition把元素完全分到一边，是最差情况，算法退化为O(n2)。

快速排序2.0

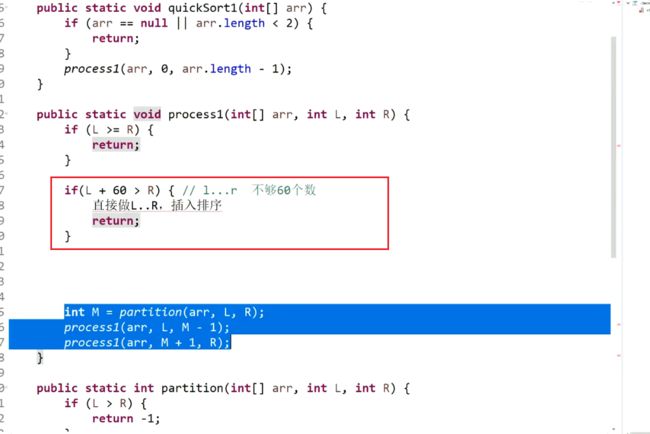
快速排序3.0

快排3.0才是我们使用的快排。时间复杂度以最坏情况来算，而快排3.0的最差情况是个概率事件，1/N的概率为最差情况，长期统一估算时间复杂度就当做O(N * logN)

上述分两个区，分三个区和快速排序的代码如下：

package class05;

public class Code02_PartitionAndQuickSort {

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

	// arr[L..R]上，以arr[R]位置的数做划分值
	// <= X > X
	// <= X X
	// 划分为两个区的代码
	public static int partition(int[] arr, int L, int R) {
		if (L > R) {
			return -1;
		}
		if (L == R) {
			return L;
		}
		int lessEqual = L - 1;
		int index = L;
		while (index < R) {
			if (arr[index] <= arr[R]) {
				swap(arr, index, ++lessEqual);
			}
			index++;
		}
		swap(arr, ++lessEqual, R);
		return lessEqual;
	}

	// arr[L...R] 玩荷兰国旗问题的划分，以arr[R]做划分值
	//  arr[R]
	// 划分为三个区的代码
	public static int[] netherlandsFlag(int[] arr, int L, int R) {
		if (L > R) { // L...R L>R
			return new int[] { -1, -1 };
		}
		if (L == R) {
			return new int[] { L, R };
		}
		int less = L - 1; // < 区 右边界
		int more = R; // > 区 左边界
		int index = L;
		while (index < more) { // 当前位置，不能和 >区的左边界撞上
			if (arr[index] == arr[R]) {
				index++;
			} else if (arr[index] < arr[R]) {
//				swap(arr, less + 1, index);
//				less++;
//				index++;
				// 三个步骤一行解决：arr[i]与<区右一个位置交换;<区右扩;i++
				swap(arr, index++, ++less);
			} else { // >
				// 三个步骤一行解决：arr[i]与>区左一个位置交换;>区左扩;i不动
				swap(arr, index, --more);
			}
		}
		// 这行我们把数组的最后一个数与 >区 的左边界交换，此行结束后，more不再是>区 的左边界而是=区的右边位置
		swap(arr, more, R); // <[R]   =[R]   >[R]
		// 返回数组的长度为2，数组的第一个数是=区的左边位置，数组的第二个数是=区的右边位置
		return new int[] { less + 1, more };
	}

	public static void quickSort1(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		process1(arr, 0, arr.length - 1);
	}

	public static void process1(int[] arr, int L, int R) {
		if (L >= R) {
			return;
		}
		// L..R partition arr[R] [ <=arr[R] arr[R] >arr[R] ]
		int M = partition(arr, L, R);
		process1(arr, L, M - 1);
		process1(arr, M + 1, R);
	}
	
	public static void quickSort2(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		process2(arr, 0, arr.length - 1);
	}

	// arr[L...R] 排有序，快排2.0方式
	public static void process2(int[] arr, int L, int R) {
		if (L >= R) {
			return;
		}
		// [ equalArea[0]  ,  equalArea[0]]
		int[] equalArea = netherlandsFlag(arr, L, R);
		process2(arr, L, equalArea[0] - 1);
		process2(arr, equalArea[1] + 1, R);
	}
	
	public static void quickSort3(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		process3(arr, 0, arr.length - 1);
	}

	public static void process3(int[] arr, int L, int R) {
		if (L >= R) {
			return;
		}
		swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
		int[] equalArea = netherlandsFlag(arr, L, R);
		process3(arr, L, equalArea[0] - 1);
		process3(arr, equalArea[1] + 1, R);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			int[] arr3 = copyArray(arr1);
			quickSort1(arr1);
			quickSort2(arr2);
			quickSort3(arr3);
			if (!isEqual(arr1, arr2) || !isEqual(arr2, arr3)) {
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Oops!");

	}

}

随机快排的时间复杂度分析

（1）通过分析知道，划分值越靠近中间，性能越好；越靠近两边，性能越差。
（2）随机选一个数进行划分的目的就是让好情况和差情况都变成概率事件。
（3）把每一种情况都列出来，会有每种情况下的时间复杂度，但概率都是1/N
（4）那么所有情况都考虑，时间复杂度就是这种概率模型下的长期期望！
时间复杂度O(N * logN)，额外空间复杂度O(logN)都是这么来的。

额外空间复杂度：

四.比较器与堆

1.比较器

（1）比较器的实质就是重载比较运算符
（2）比较器可以很好的应用在特殊标准的排序上
（3）比较器可以很好的应用在根据特殊标准排序的结构上
（4）写代码变得异常容易，还用于范型编程

2.堆结构

（1）堆结构就是用数组实现的完全二叉树结构
（2）完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
（3）完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
（4）堆结构的heaplnsert与heapify操作
（5）堆结构的增大和减少
（6）优先级队列结构，就是堆结构

关于树的介绍，见其他博客：
满二叉树、完全二叉树、平衡二叉树、最优二叉树

什么是二叉树（包含满二叉树和完全二叉树）

（1）完全二叉树

二叉树的某一层是满的；或者在不满的那一层（只能是最后一层）从左到右是变满的状态中，中间没有空。

完全二叉树案例：

非完全二叉树案例：

没满的那一层并不是从左到右依次变满的

（2）数组形式表示二叉树。

完全二叉树可以用二叉树表示，在堆中我们用堆表示。数组形式也可以做一个对应的二叉树。

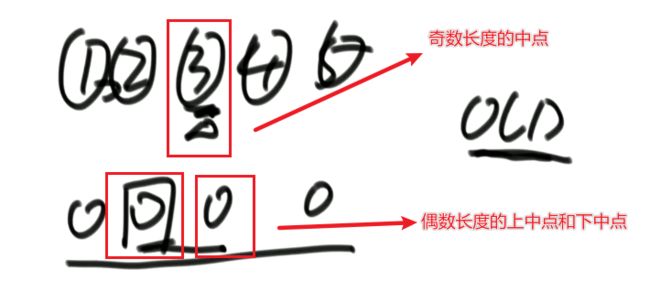
对于数组从0开始使用的节点：

所有节点， 找左子节点为2 * i + 1；i为当前节点的位置
找右子节点为2 * i + 2；

除了根节点以外的节点，找父节点为 (i - 1) / 2； => 去尾法，即向下兼容取整数。

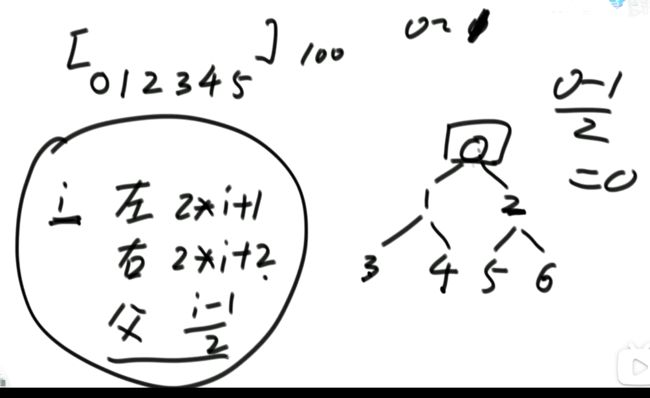
注意：有的实现，数组的0位置弃而不用。

对于数组从1位置开始使用的节点：

（3）我们这里使用数组从0开始的实现。

对于几个数组想要实现为完全二叉树，假设数组arr长度为100，我们可以考虑设置一个变量size，用size来限制数组的第0到多少位置为一颗完全二叉树。

注意：
堆在结构上是一棵完全二叉树，完全二叉树上又有别的要求，分为大根堆和小根堆。
完全二叉树未必是堆。不是大根堆也不是小根堆那就不是堆。

大根堆：每一棵子树最大值都是自己头节点的值，如下图：

小根堆：每一棵子树最小值都是自己头节点的值，图省略。

（4）题目：依次给数字，每给一个数字让你组成大根堆。

注意：

找父节点和子节点的流程上面有描述。
每个添加的数字都放在数组arr中，由0位置逐渐增加。我们是用数组形成组建二叉树，并不断调整组成大根堆的。

流程：

给第1个数字3，heapSize = 1，只有一个数4，此时组成大根堆。
给第2个数字2，heapSize = 2，2作为子节点是小于父节点4的，此时组成大根堆。
给第3个数字4，heapSize = 3，3作为子节点是大于父节点4的，此时不组成大根堆，我们把4和3交换，此时组成大根堆。
给第4个数字3，heapSize = 4，3作为子节点是小于父节点2的，此时不组成大根堆，我们把3和2交换，此时组成大根堆。

调整为大根堆交换时的代价：

如果添加了N个数字，那么N个数字构成的数字所组成的二叉树的高度是logN。因此，新添加一个数后，会和其父节点比较，最差情况下会一直比较交换到根节点，即比较了二叉树的高度的次数。

新增要求：

返回到目前为止所有数字的最大值并且把最大值删除后这依然是个大根堆。

解法：
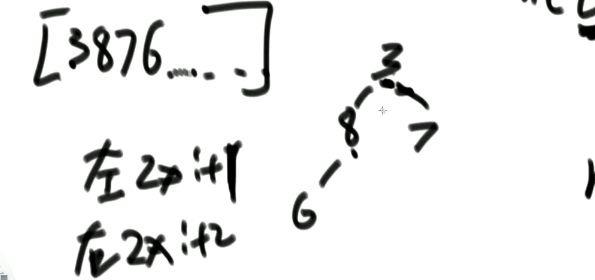
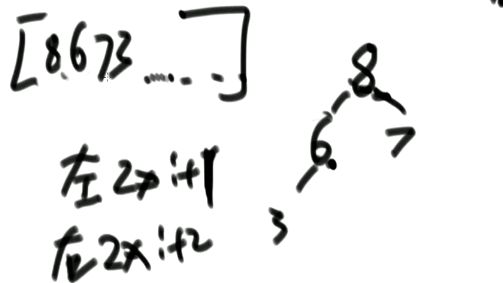
若实现完全二叉树的方式是一个数组，且有一个变量为数组的大小heapSize，则在实现大根堆后，最大值就是arr[0]，int t = arr[0]…return t; 我们交换arr[0]和arr[9]或者arr[0]=arr[9]，并把heapSize = 9;
然而此时我们不能保证原先的arr[9]即新的arr[0]为最大值，即不能保证为大根堆。接下来我们可以进行heapify操作，新arr[0]与两个子节点比较，若新arr[0]比两个子结点中较大的子节点小，则交换新arr[0]和两个子结点中较大的子节点，不断进行heapify操作。

最后就调整成了大根堆。

代码如下：

package class06;

import java.util.Comparator;
import java.util.PriorityQueue;

public class Code02_Heap {

	public static class MyMaxHeap {
		private int[] heap;
		private final int limit;
		private int heapSize;

		public MyMaxHeap(int limit) {
			heap = new int[limit];
			this.limit = limit;
			heapSize = 0;
		}

		public boolean isEmpty() {
			return heapSize == 0;
		}

		public boolean isFull() {
			return heapSize == limit;
		}

		public void push(int value) {
			if (heapSize == limit) {
				throw new RuntimeException("heap is full");
			}
			heap[heapSize] = value;
			// value heapSize
			heapInsert(heap, heapSize++);
		}

		// 用户此时，让你返回最大值，并且在大根堆中，把最大值删掉
		// 剩下的数，依然保持大根堆组织
		public int pop() {
			int ans = heap[0];
			swap(heap, 0, --heapSize);
			heapify(heap, 0, heapSize);
			return ans;
		}

		// 新加进来的数，现在停在了index位置，请依次往上移动，
		// 移动到0位置，或者干不掉自己的父亲了，停！
		private void heapInsert(int[] arr, int index) {
			// [index] [index-1]/2
			// 停止循环的条件：index == 0即当前值已经交换到了顶部或者arr[index] 不比arr[index父]大了。
			// 如果当前的值比父亲节点的值大，则交换两个数。然后在向上比较
			while (arr[index] > arr[(index - 1) / 2]) {
				swap(arr, index, (index - 1) / 2);
				index = (index - 1) / 2;
			}
		}

		// 从index位置，往下看，不断的下沉
		// 停：较大的孩子都不再比index位置的数大；已经没孩子了
		private void heapify(int[] arr, int index, int heapSize) {
			int left = index * 2 + 1;
			while (left < heapSize) { // 如果有左孩子，有没有右孩子，可能有可能没有！
				// 把较大孩子的下标，给largest
				int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
				largest = arr[largest] > arr[index] ? largest : index;
				if (largest == index) {
					break;
				}
				// index和较大孩子，要互换
				swap(arr, largest, index);
				index = largest;
				left = index * 2 + 1;
			}
		}

		private void swap(int[] arr, int i, int j) {
			int tmp = arr[i];
			arr[i] = arr[j];
			arr[j] = tmp;
		}

	}

	public static class RightMaxHeap {
		private int[] arr;
		private final int limit;
		private int size;

		public RightMaxHeap(int limit) {
			arr = new int[limit];
			this.limit = limit;
			size = 0;
		}

		public boolean isEmpty() {
			return size == 0;
		}

		public boolean isFull() {
			return size == limit;
		}

		public void push(int value) {
			if (size == limit) {
				throw new RuntimeException("heap is full");
			}
			arr[size++] = value;
		}

		public int pop() {
			int maxIndex = 0;
			for (int i = 1; i < size; i++) {
				if (arr[i] > arr[maxIndex]) {
					maxIndex = i;
				}
			}
			int ans = arr[maxIndex];
			arr[maxIndex] = arr[--size];
			return ans;
		}

	}

	public static class MyComparator implements Comparator<Integer> {

		@Override
		public int compare(Integer o1, Integer o2) {
			return o2 - o1;
		}

	}

	public static void main(String[] args) {

		// 小根堆
		PriorityQueue<Integer> heap = new PriorityQueue<>(new MyComparator());
		heap.add(5);
		heap.add(5);
		heap.add(5);
		heap.add(3);
		// 5 , 3
		System.out.println(heap.peek());
		heap.add(7);
		heap.add(0);
		heap.add(7);
		heap.add(0);
		heap.add(7);
		heap.add(0);
		System.out.println(heap.peek());
		while (!heap.isEmpty()) {
			System.out.println(heap.poll());
		}

		int value = 1000;
		int limit = 100;
		int testTimes = 1000000;
		for (int i = 0; i < testTimes; i++) {
			int curLimit = (int) (Math.random() * limit) + 1;
			MyMaxHeap my = new MyMaxHeap(curLimit);
			RightMaxHeap test = new RightMaxHeap(curLimit);
			int curOpTimes = (int) (Math.random() * limit);
			for (int j = 0; j < curOpTimes; j++) {
				if (my.isEmpty() != test.isEmpty()) {
					System.out.println("Oops!");
				}
				if (my.isFull() != test.isFull()) {
					System.out.println("Oops!");
				}
				if (my.isEmpty()) {
					int curValue = (int) (Math.random() * value);
					my.push(curValue);
					test.push(curValue);
				} else if (my.isFull()) {
					if (my.pop() != test.pop()) {
						System.out.println("Oops!");
					}
				} else {
					if (Math.random() < 0.5) {
						int curValue = (int) (Math.random() * value);
						my.push(curValue);
						test.push(curValue);
					} else {
						if (my.pop() != test.pop()) {
							System.out.println("Oops!");
						}
					}
				}
			}
		}
		System.out.println("finish!");

	}

}

这也是大根堆：

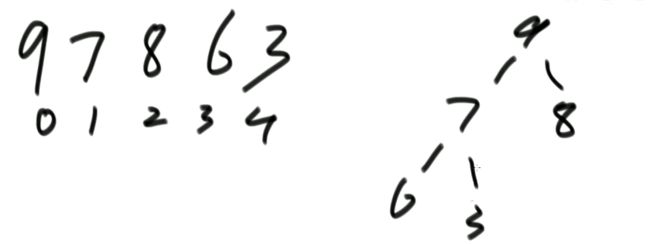
替换后：


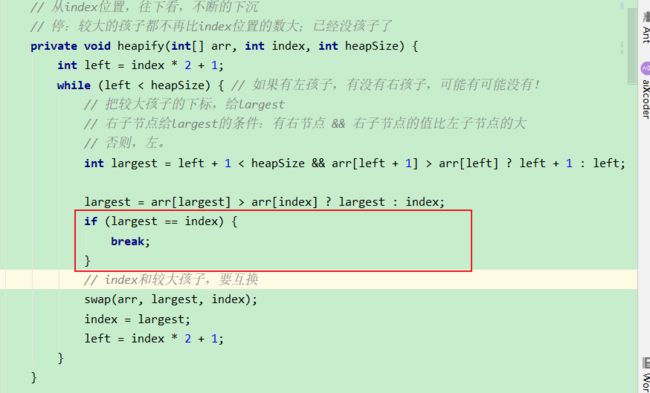
上述代码中if成立的条件：



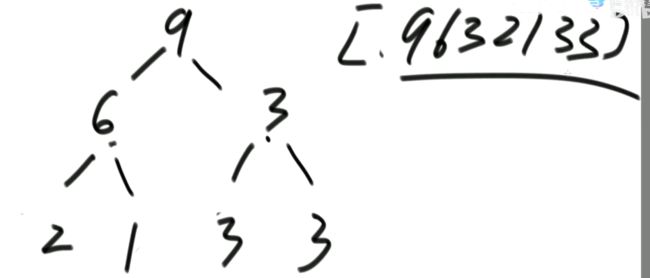
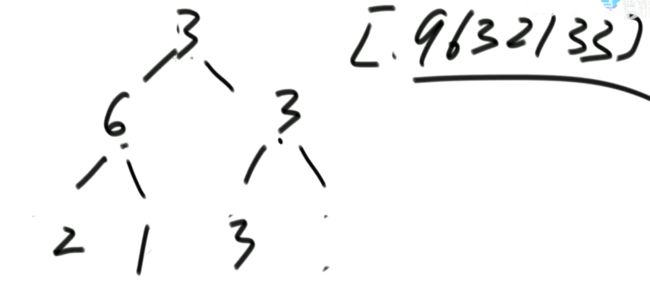
heapify操作的时间复杂度也是logN

（5）堆结构比堆排序重要得多。上面所述都为堆结构，下面我们来看堆排序：

1. 先让整个数组都变成大根堆结构，建立堆的过程：
   从上到下的方法，时间复杂度为O(NlogN)；
   从下到上的方法，时间复杂度为O(N)
2. 把堆的最大值和堆末尾的值交换,然后减少堆的大小之后，再去调整堆，一直周而复始，时间复杂度为O(NlogN)
3. 堆的大小减小成0之后，排序完成。

举例：一个无序数组arr[]，里面有N个数且处于无序状态。第一步我们把它变为大根堆.此时0位置的数是全局最大值；0位置的数与N-1位置的数交换，新0位置的数heapify，heapify后0位置的数又变了，为新新0位置，同时大根堆heapSize-1，即把第N-1位置排除掉大根堆；新新0位置的数与N-2位置的数交换，新新新0位置的数heapify，heapify后0位置的数又变了，为新新新新0位置，同时大根堆heapSize-1，即把第N-2位置排除掉大根堆.依此类推。最后整个数组就有序了。

堆排序代码如下：

package class06;

import java.util.Arrays;
import java.util.PriorityQueue;

public class Code03_HeapSort {

	// 堆排序额外空间复杂度O(1)
	public static void heapSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		// 经典：O(N*logN)
//		for (int i = 0; i < arr.length; i++) { // O(N)
//			heapInsert(arr, i); // O(logN)
//		}
		// 优化：O(N)
		for (int i = arr.length - 1; i >= 0; i--) {
			heapify(arr, i, arr.length);
		}
		int heapSize = arr.length;
		swap(arr, 0, --heapSize);
		// O(N*logN)
		while (heapSize > 0) { // O(N)
			heapify(arr, 0, heapSize); // O(logN)
			swap(arr, 0, --heapSize); // O(1)
		}
	}

	// arr[index]刚来的数，往上
	public static void heapInsert(int[] arr, int index) {
		while (arr[index] > arr[(index - 1) / 2]) {
			swap(arr, index, (index - 1) / 2);
			index = (index - 1) / 2;
		}
	}

	// arr[index]位置的数，能否往下移动
	public static void heapify(int[] arr, int index, int heapSize) {
		int left = index * 2 + 1; // 左孩子的下标
		while (left < heapSize) { // 下方还有孩子的时候
			// 两个孩子中，谁的值大，把下标给largest
			// 1）只有左孩子，left -> largest
			// 2) 同时有左孩子和右孩子，右孩子的值<= 左孩子的值，left -> largest
			// 3) 同时有左孩子和右孩子并且右孩子的值> 左孩子的值， right -> largest
			int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
			// 父和较大的孩子之间，谁的值大，把下标给largest
			largest = arr[largest] > arr[index] ? largest : index;
			if (largest == index) {
				break;
			}
			swap(arr, largest, index);
			index = largest;
			left = index * 2 + 1;
		}
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {

		// 默认小根堆
		PriorityQueue<Integer> heap = new PriorityQueue<>();
		heap.add(6);
		heap.add(8);
		heap.add(0);
		heap.add(2);
		heap.add(9);
		heap.add(1);

		while (!heap.isEmpty()) {
			System.out.println(heap.poll());
		}

		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			heapSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		heapSort(arr);
		printArray(arr);
	}

}

对于优化写法效益更好的证明：这种优化写法只在一次性给很多数的情况下才可以进行，否则只能一点一点heapInsert


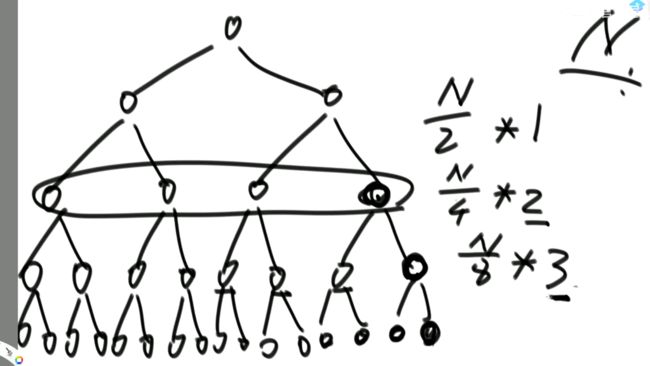
解析：共有N个数，最后一层每个数都要有一次判断操作，判断自己有无子节点。倒数第二层有一次判断操作，同时最多有一次下沉（heapify）操作。倒数第三层有一次比较操作，同时最多有2次下沉（heapify）操作。且最后一层共有N/2个数，倒数第二层有N/4个数。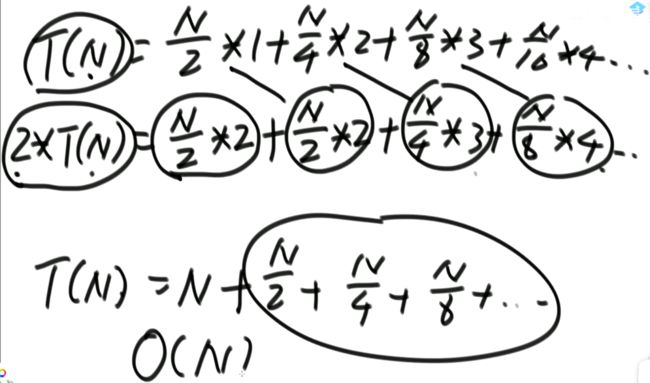

那种优化写法的时间复杂度有上述推导可知其时间复杂度是O(N)的

（6）待办：堆排序的heapInsert和heapify操作梳理一下区别

3.语言提供的堆结构VS手写的堆结构

取决于，你有没有动态改信息的需求！
语言提供的堆结构，如果你动态改数据，不保证依然有序。
手写堆结构，因为增加了对象的位置表，所以能够满足动态改信息的需求。

（1）系统实现的堆怎么用

   		// 优先级队列底层就是堆，默认小根堆
		PriorityQueue<Integer> heap = new PriorityQueue<>();
		heap.add(6);
		heap.add(8);
		heap.add(0);
		heap.add(2);
		heap.add(9);
		heap.add(1);

		while (!heap.isEmpty()) {
			System.out.println(heap.poll());
		}

（2）与堆有关的题目

已知一个几乎有序的数组。几乎有序是指如果把数组排好顺序的话，每个
元素移动的距离一定不超过k，并且k相对于数组长度来说是比较小的。
请选择一个合适的排序策略，对这个数组进行排序。

解析：给定一个数组arr[]，且k=5，意思也就是如果是的这个数组有序的话，每个元素移动的距离不会超过5.

解法：
生成一个小根堆。把arr[]数组的0位置的数到k位置的数（即前k+1个数）放到小根堆中去（0到k是因为每个元素让其有序的移动距离不超过5，k位置到0位置移动的距离正好等于5）.0位置的数到k位置的数先放到小根堆中（之后小根堆有6个数）找到最小值再把最小值放到数组的0位置（此时小根堆只有5个数），然后再把arr[]数组的6位置的数放到小根堆中（之后小根堆有6个数），找到小根堆中当前的最小值，再放到arr[]数组的1位置的数，依此类推。
小根堆的时间复杂度是logK级别的。整体时间复杂度是N*logK的。我们也可以第一次放2k+1个数到小根堆中，每次弹k个数，放k个数也可以。但是小根堆的时间复杂度会变成log2K级别，时间复杂度不变，常数变大。

代码如下：

package class06;

import java.util.Arrays;
import java.util.PriorityQueue;

public class Code04_SortArrayDistanceLessK {

	public static void sortedArrDistanceLessK(int[] arr, int k) {
		if (k == 0) {
			return;
		}
		// 优先级队列底层就是堆，默认小根堆
		PriorityQueue<Integer> heap = new PriorityQueue<>();
		int index = 0;
		// 0...K-1
		for (; index <= Math.min(arr.length - 1, k - 1); index++) {
			heap.add(arr[index]);
		}
		int i = 0;
		for (; index < arr.length; i++, index++) {
			// 先加再弹，先弹再加是一样的。
			heap.add(arr[index]);
			arr[i] = heap.poll();
		}
		// 最后五个数，在小根堆中已经是有序的了，也没有数再添加其中，依次弹出即可
		while (!heap.isEmpty()) {
			arr[i++] = heap.poll();
		}
	}

	// for test
	public static void comparator(int[] arr, int k) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] randomArrayNoMoveMoreK(int maxSize, int maxValue, int K) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
		}
		// 先排个序
		Arrays.sort(arr);
		// 然后开始随意交换，但是保证每个数距离不超过K
		// swap[i] == true, 表示i位置已经参与过交换
		// swap[i] == false, 表示i位置没有参与过交换
		boolean[] isSwap = new boolean[arr.length];
		for (int i = 0; i < arr.length; i++) {
			int j = Math.min(i + (int) (Math.random() * (K + 1)), arr.length - 1);
			if (!isSwap[i] && !isSwap[j]) {
				isSwap[i] = true;
				isSwap[j] = true;
				int tmp = arr[i];
				arr[i] = arr[j];
				arr[j] = tmp;
			}
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		System.out.println("test begin");
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int k = (int) (Math.random() * maxSize) + 1;
			int[] arr = randomArrayNoMoveMoreK(maxSize, maxValue, k);
			int[] arr1 = copyArray(arr);
			int[] arr2 = copyArray(arr);
			sortedArrDistanceLessK(arr1, k);
			comparator(arr2, k);
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				System.out.println("K : " + k);
				printArray(arr);
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
	}

}

（3）比较器

1. 比较器的实质就是重载比较运算符
2. 比较器可以很好的应用在特殊标准的排序上
3. 比较器可以很好的应用在根据特殊标准排序的结构上
4. 写代码变得异常容易，还用于范型编程

任何比较器，我们定义一个T类型的样本为O1，另一个T类型的样本为O2.比较样本O1和O2

O1排在前面，则返回-1
O2排在前面，则返回1
在你自己定义的比较标准下，O1和O2一样，则返回0。

代码如下：

package class06;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.TreeMap;

public class Code01_Comparator {

	public static class Student {
		public String name;
		public int id;
		public int age;

		public Student(String name, int id, int age) {
			this.name = name;
			this.id = id;
			this.age = age;
		}
	}

	// 任何比较器：
	// compare方法里，遵循一个统一的规范：
	// 返回负数的时候，认为第一个参数应该排在前面
	// 返回正数的时候，认为第二个参数应该排在前面
	// 返回0的时候，认为无所谓谁放前面
	public static class IdShengAgeJiangOrder implements Comparator<Student> {

		// 根据id从小到大，但是如果id一样，按照年龄从大到小
		@Override
		public int compare(Student o1, Student o2) {
			return o1.id != o2.id ? (o1.id - o2.id) : (o2.age - o1.age);
		}

	}

	// Id升序的比较器
	public static class IdAscendingComparator implements Comparator<Student> {

		// 返回负数的时候，第一个参数排在前面
		// 返回正数的时候，第二个参数排在前面
		// 返回0的时候，谁在前面无所谓
		@Override
		public int compare(Student o1, Student o2) {

//			if(o1.id < o2.id) {
//				return -1;
//			} else if (o1.id > o2.id) {
//				return 1;
//			} else {
//				return 0;
//			}
			// 下面一行为上面几行的简略写法
			return o1.id - o2.id;
		}

	}

	// Id降序的比较器
	public static class IdDescendingComparator implements Comparator<Student> {

		@Override
		public int compare(Student o1, Student o2) {
			return o2.id - o1.id;
		}

	}

	// 先按照id排序，id小的，放前面；
	// id一样，age大的，前面；
	public static class IdInAgeDe implements Comparator<Student> {

		@Override
		public int compare(Student o1, Student o2) {
			return o1.id != o2.id ? o1.id - o2.id : (o2.age - o1.age);
		}

	}

	public static void printStudents(Student[] students) {
		for (Student student : students) {
			System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
		}
	}

	public static void printArray(Integer[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static class MyComp implements Comparator<Integer> {

		@Override
		public int compare(Integer o1, Integer o2) {
			return o2 - o1;
		}

	}

	public static class AComp implements Comparator<Integer> {

		// 如果返回负数，认为第一个参数应该拍在前面
		// 如果返回正数，认为第二个参数应该拍在前面
		// 如果返回0，认为谁放前面都行
		@Override
		public int compare(Integer arg0, Integer arg1) {

			return arg1 - arg0;

//			return 0;
		}

	}

	public static void main(String[] args) {

		Integer[] arr = { 5, 4, 3, 2, 7, 9, 1, 0 };

		Arrays.sort(arr, new AComp());

		for (int i = 0; i < arr.length; i++) {
			System.out.println(arr[i]);
		}

		System.out.println("===========================");

		Student student1 = new Student("A", 4, 40);
		Student student2 = new Student("B", 4, 21);
		Student student3 = new Student("C", 3, 12);
		Student student4 = new Student("D", 3, 62);
		Student student5 = new Student("E", 3, 42);
		// D E C A B

		Student[] students = new Student[] { student1, student2, student3, student4, student5 };
		System.out.println("第一条打印");

		Arrays.sort(students, new IdShengAgeJiangOrder());
		for (int i = 0; i < students.length; i++) {
			Student s = students[i];
			System.out.println(s.name + "," + s.id + "," + s.age);
		}

		System.out.println("第二条打印");
		ArrayList<Student> studentList = new ArrayList<>();
		studentList.add(student1);
		studentList.add(student2);
		studentList.add(student3);
		studentList.add(student4);
		studentList.add(student5);
		studentList.sort(new IdShengAgeJiangOrder());
		for (int i = 0; i < studentList.size(); i++) {
			Student s = studentList.get(i);
			System.out.println(s.name + "," + s.id + "," + s.age);
		}
		// N * logN
		System.out.println("第三条打印");
		student1 = new Student("A", 4, 40);
		student2 = new Student("B", 4, 21);
		student3 = new Student("C", 4, 12);
		student4 = new Student("D", 4, 62);
		student5 = new Student("E", 4, 42);
		TreeMap<Student, String> treeMap = new TreeMap<>((a, b) -> (a.id - b.id));
		treeMap.put(student1, "我是学生1，我的名字叫A");
		treeMap.put(student2, "我是学生2，我的名字叫B");
		treeMap.put(student3, "我是学生3，我的名字叫C");
		treeMap.put(student4, "我是学生4，我的名字叫D");
		treeMap.put(student5, "我是学生5，我的名字叫E");
		for (Student s : treeMap.keySet()) {
			System.out.println(s.name + "," + s.id + "," + s.age);
		}

	}

}
 

比较器可以很好的应用在特殊标准的排序上

举例： 比较器用在大根堆排序上。

同时有序表等也可以使用比较器。写代码排序可以考虑调用系统实现的比较器比较，而不用写排序算法。

字典序待了解

（4）手写堆结构的情况（这里的代码有些不完善）

有些时候我们把数据按照堆结构实现后，还要修改数据信息，这时就不能保证之后的堆结构依然正确。

迪杰斯特拉算法就存在手动改写堆的优化。这是系统提供的堆不好的地方，有的语言也会提供让它重新有序的方法，是在每一个点上都进行heapInsert操作，而这代价就高了。

自己写的堆结构：indexMap是记录自己样本在堆中所在的位置，这样一来修改数据后想要依然保持对接二狗就不需要每一个点上都进行heapInsert操作了。

注意：刷题过程中若需要用到的堆在之后还要修改一些东西自己写一个堆最好。

对于heapInsert和heapify： 上述已证明heapify的时间复杂度，对于heapInsert还未证明。heapify的时间复杂度是优于heapInsert的。
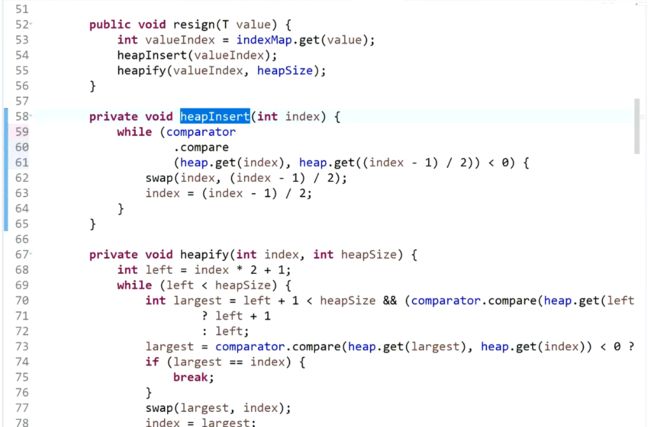
heapInsert为从上往下。
heapify为从下往上，从下往上的每一个点都会向下看。

从上往下建堆，节点少的时间复杂度低，节点多的时间复杂度高。

从下往上建堆，节点少的时间复杂度高，节点多的时间复杂度低。

相等的样本数量，为什么从下往上的交换比从上往下的小。

证明从上往下收敛不到O(n)：

举例：若有N个样本，时间复杂度是O(?)；则有2N个样本，时间复杂度也是O(?)，因为复杂度本身是不考虑常数和系数的。

解析：假设N个样本时，时间复杂度收敛到O(N)；2N个样本时，先把前N个节点做出一个堆来，做出N个节点时，这个堆的高度是logN的，后N个节点向堆中插入的时候，其复杂度不可能是logN的，每个点插入到堆中的时间复杂度是logN，所以时间复杂度应该是O(N*logN)的。由此可知，在N个样本时，其时间复杂度不可能收敛到O(N)的。

提示：证明一个复杂度能收敛到一个水平上，我们可以把样本数量再扩充一倍。若扩充一倍后的时间复杂度还能收敛到原先样本数量时的时间复杂度，则得证。

五、tire、桶排序、排序总结

1.前缀树

1. 单个字符串中，字符从前到后的加到一棵多叉树上
2. 字符放在路上，节点上有专属的数据项(常见的是pass和end值)
3. 所有样本都这样添加，如果没有路就新建，如有路就复用
4. 沿途节点的pass值增加1，每个字符串结束时来到的节点end值增加1

举例：

接下来到"abd"字符串，一个新字符串要从头开始看。

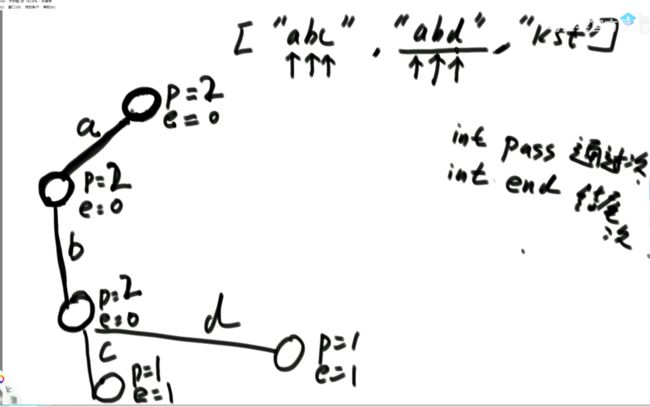
接下来到"kst"字符串：

若又新加一个字符串"ab"：

若新加一个字符串"a"：

注意：
若新建字符串"gab"，这里注意g开头是一条新路，前面创建的a,b路不会复用。无路新建，有路复用。
若所有字符串总的字符数量是N的话，把整棵树建好就是O(N)的代价，每处理一个字符的代价都是O(1)。

若此时有个需求，查询"abd"字符串被加入了几次。我们查看前缀树即可，如下图：

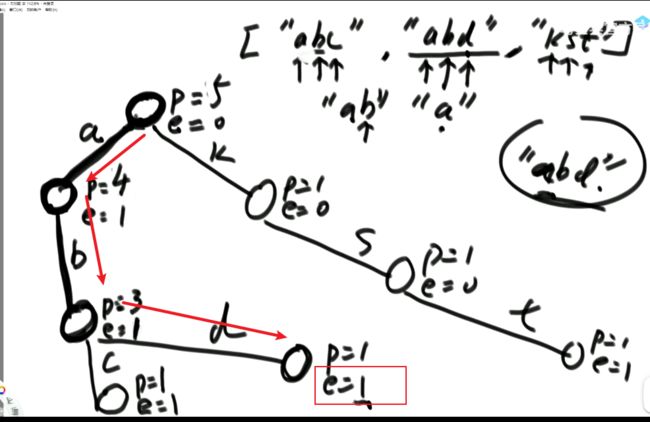
查看前缀树可知沿着a,b,d路线的e=1，由此可知 ，"abd"被加入了1次。

我们发现，上述功能哈希表也能做。但是接下来的功能哈希表就做不了了。

要求：查询有多少个字符串以"a"做前缀。

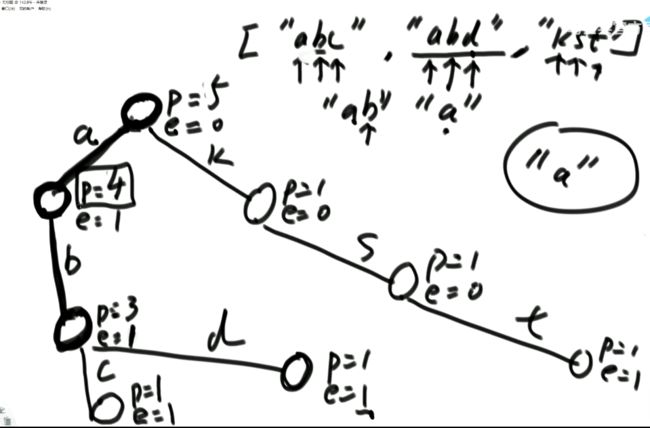
我们从图中可知，a线路的p=4，所以有4个字符串以"a"做前缀。唯有从根节点出发的才可以通过这种方法查看有多少个字符串以某字符为前缀。

代码如下（两种方式实现前缀树）：

package class08;

import java.util.HashMap;

// 该程序完全正确
public class Code02_TrieTree {

	public static class Node1 {
		public int pass;
		public int end;
		public Node1[] nexts;

		// char tmp = 'b'  (tmp - 'a')
		public Node1() {
			pass = 0;
			end = 0;
			// 0    a
			// 1    b
			// 2    c
			// ..   ..
			// 25   z
			// nexts[i] == null   i方向的路不存在
			// nexts[i] != null   i方向的路存在
			nexts = new Node1[26];
		}
	}

	public static class Trie1 {
		private Node1 root;

		public Trie1() {
			root = new Node1();
		}

		public void insert(String word) {
			if (word == null) {
				return;
			}
			char[] str = word.toCharArray();
			Node1 node = root;
			node.pass++;
			int path = 0;
			for (int i = 0; i < str.length; i++) { // 从左往右遍历字符
				path = str[i] - 'a'; // 字符-a的ascii码。由字符，对应成走向哪条路（-a是为了将字符对应到0-26的下标   a-a就是0下标）
				if (node.nexts[path] == null) {
					node.nexts[path] = new Node1();
				}
				node = node.nexts[path];
				node.pass++;
			}
			node.end++;
		}

		public void delete(String word) {
			if (search(word) != 0) {
				char[] chs = word.toCharArray();
				Node1 node = root;
				node.pass--;
				int path = 0;
				for (int i = 0; i < chs.length; i++) {
					path = chs[i] - 'a';
					if (--node.nexts[path].pass == 0) {
						node.nexts[path] = null;
						return;
					}
					node = node.nexts[path];
				}
				node.end--;
			}
		}

		// word这个单词之前加入过几次
		public int search(String word) {
			if (word == null) {
				return 0;
			}
			char[] chs = word.toCharArray();
			Node1 node = root;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = chs[i] - 'a';
				if (node.nexts[index] == null) {
					return 0;
				}
				node = node.nexts[index];
			}
			return node.end;
		}

		// 所有加入的字符串中，有几个是以pre这个字符串作为前缀的
		public int prefixNumber(String pre) {
			if (pre == null) {
				return 0;
			}
			char[] chs = pre.toCharArray();
			Node1 node = root;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = chs[i] - 'a';
				if (node.nexts[index] == null) {
					return 0;
				}
				node = node.nexts[index];
			}
			return node.pass;
		}
	}

	public static class Node2 {
		public int pass;
		public int end;
		public HashMap<Integer, Node2> nexts;

		public Node2() {
			pass = 0;
			end = 0;
			nexts = new HashMap<>();
		}
	}

	public static class Trie2 {
		private Node2 root;

		public Trie2() {
			root = new Node2();
		}

		public void insert(String word) {
			if (word == null) {
				return;
			}
			char[] chs = word.toCharArray();
			Node2 node = root;
			node.pass++;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = (int) chs[i];
				if (!node.nexts.containsKey(index)) {
					node.nexts.put(index, new Node2());
				}
				node = node.nexts.get(index);
				node.pass++;
			}
			node.end++;
		}

		public void delete(String word) {
			if (search(word) != 0) {
				char[] chs = word.toCharArray();
				Node2 node = root;
				node.pass--;
				int index = 0;
				for (int i = 0; i < chs.length; i++) {
					index = (int) chs[i];
					if (--node.nexts.get(index).pass == 0) {
						node.nexts.remove(index);
						return;
					}
					node = node.nexts.get(index);
				}
				node.end--;
			}
		}

		// word这个单词之前加入过几次
		public int search(String word) {
			if (word == null) {
				return 0;
			}
			char[] chs = word.toCharArray();
			Node2 node = root;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = (int) chs[i];
				if (!node.nexts.containsKey(index)) {
					return 0;
				}
				node = node.nexts.get(index);
			}
			return node.end;
		}

		// 所有加入的字符串中，有几个是以pre这个字符串作为前缀的
		public int prefixNumber(String pre) {
			if (pre == null) {
				return 0;
			}
			char[] chs = pre.toCharArray();
			Node2 node = root;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = (int) chs[i];
				if (!node.nexts.containsKey(index)) {
					return 0;
				}
				node = node.nexts.get(index);
			}
			return node.pass;
		}
	}

	public static class Right {

		private HashMap<String, Integer> box;

		public Right() {
			box = new HashMap<>();
		}

		public void insert(String word) {
			if (!box.containsKey(word)) {
				box.put(word, 1);
			} else {
				box.put(word, box.get(word) + 1);
			}
		}

		public void delete(String word) {
			if (box.containsKey(word)) {
				if (box.get(word) == 1) {
					box.remove(word);
				} else {
					box.put(word, box.get(word) - 1);
				}
			}
		}

		public int search(String word) {
			if (!box.containsKey(word)) {
				return 0;
			} else {
				return box.get(word);
			}
		}

		public int prefixNumber(String pre) {
			int count = 0;
			for (String cur : box.keySet()) {
				if (cur.startsWith(pre)) {
					count += box.get(cur);
				}
			}
			return count;
		}
	}

	// for test
	public static String generateRandomString(int strLen) {
		char[] ans = new char[(int) (Math.random() * strLen) + 1];
		for (int i = 0; i < ans.length; i++) {
			int value = (int) (Math.random() * 6);
			ans[i] = (char) (97 + value);
		}
		return String.valueOf(ans);
	}

	// for test
	public static String[] generateRandomStringArray(int arrLen, int strLen) {
		String[] ans = new String[(int) (Math.random() * arrLen) + 1];
		for (int i = 0; i < ans.length; i++) {
			ans[i] = generateRandomString(strLen);
		}
		return ans;
	}

	public static void main(String[] args) {
		int arrLen = 100;
		int strLen = 20;
		int testTimes = 100000;
		for (int i = 0; i < testTimes; i++) {
			String[] arr = generateRandomStringArray(arrLen, strLen);
			Trie1 trie1 = new Trie1();
			Trie2 trie2 = new Trie2();
			Right right = new Right();
			for (int j = 0; j < arr.length; j++) {
				double decide = Math.random();
				if (decide < 0.25) {
					trie1.insert(arr[j]);
					trie2.insert(arr[j]);
					right.insert(arr[j]);
				} else if (decide < 0.5) {
					trie1.delete(arr[j]);
					trie2.delete(arr[j]);
					right.delete(arr[j]);
				} else if (decide < 0.75) {
					int ans1 = trie1.search(arr[j]);
					int ans2 = trie2.search(arr[j]);
					int ans3 = right.search(arr[j]);
					if (ans1 != ans2 || ans2 != ans3) {
						System.out.println("Oops!");
					}
				} else {
					int ans1 = trie1.prefixNumber(arr[j]);
					int ans2 = trie2.prefixNumber(arr[j]);
					int ans3 = right.prefixNumber(arr[j]);
					if (ans1 != ans2 || ans2 != ans3) {
						System.out.println("Oops!");
					}
				}
			}
		}
		System.out.println("finish!");

	}

}

注意：并不会出现形成环的情况，如下图：

2.例题

设计一种结构。用户可以:
（1）void insert(String str) 添加某个字符串,可以重复添加,每次算1个
（2）int search(String str) 查询某个字符串在结构中还有几个
（3）void delete(String str) 删掉某个字符串,可以重复删除,每次算1个
（4）int prefixnumber(String str) 查询有多少个字符串,是以str做前缀的

见1的代码

3.前缀树路的实现方式

（1）固定数组实现
（2）哈希表实现

见1的代码

4.不基于比较的排序

桶排序思想下的排序。计数排序&基数排序
（1）桶排序思想下的排序都是不基于比较的排序
（2）时间复杂度为O(N)，额外空间负载度O(M)
（3）应用范围有限，需要样本的数据状况满足桶的划分

注意：
桶排序是一种思想，用容器（桶）来帮助进行排序。
所有桶排序思想下的排序都要对数据状况本身有要求，即数据状况比较狭隘的情况下桶排序是一个不错的选择。

（1）计数排序

问题：假设有一个数组arr[]，存放的是员工的年龄age，0 <= age <= 200。要求对arr[]进行排序。

解法：我们创建一个help数组，数组大小为201.即arr数组下标由0到200.下标代表的是年龄。下标上的数代表的是出现的次数。若help[0] = 2意味着年龄为0的有2人。在arr[]数组中0出现了2次。之后我们按顺序把help数组的记录写回到arr[]数组中。这种排序叫做计数排序，时间复杂度是O(N)，因为这个只对arr[]数组进行了依次遍历。我们可以把help数组的0-200位置看为201个桶

计数排序特点：没有产生比较

补充：HashMap不是排序，是无序的，底层是散列表。

代码如下：

package class08;

import java.util.Arrays;

public class Code03_CountSort {

	// only for 0~200 value
	public static void countSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int max = Integer.MIN_VALUE;
		for (int i = 0; i < arr.length; i++) {
			max = Math.max(max, arr[i]);
		}
		int[] bucket = new int[max + 1];
		for (int i = 0; i < arr.length; i++) {
			bucket[arr[i]]++;
		}
		int i = 0;
		for (int j = 0; j < bucket.length; j++) {
			while (bucket[j]-- > 0) {
				arr[i++] = j;
			}
		}
	}

	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 150;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			countSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		countSort(arr);
		printArray(arr);

	}

}

（2）基数排序

使用前提：数字为非负数且满足十进制。

举例：假设有一个数组如图：

解法：
第一步：遍历1遍，找最大值为100，它是三位数的，那么我们再给其他不足三位数的补齐为三位数，如图：

第二步，准备10个桶：10个桶都是队列，先进先出

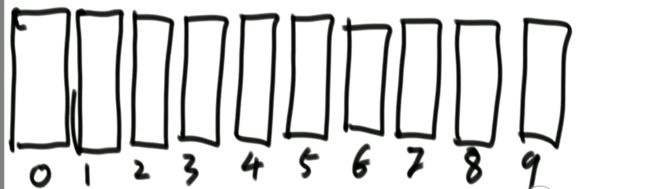
第三步，根据个位数字进桶。

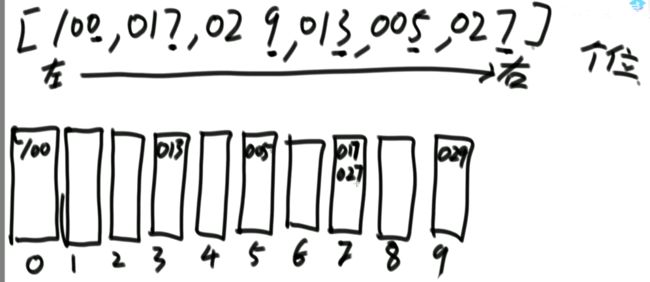
第四步，桶从左往右向数组里倒数字。

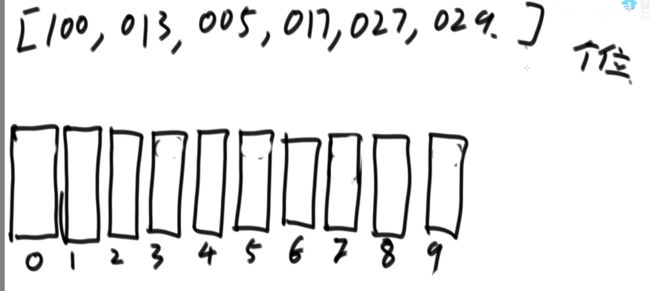
第五步，根据十位数字进桶。

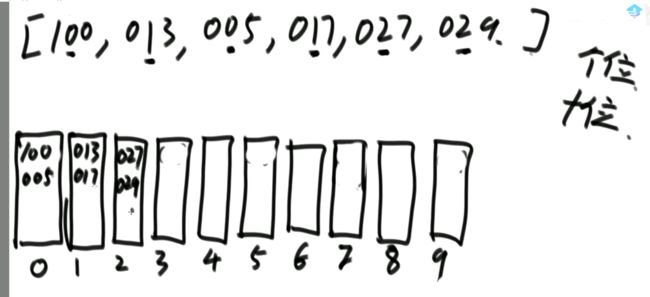
第六步，桶从左往右向数组里倒数字。

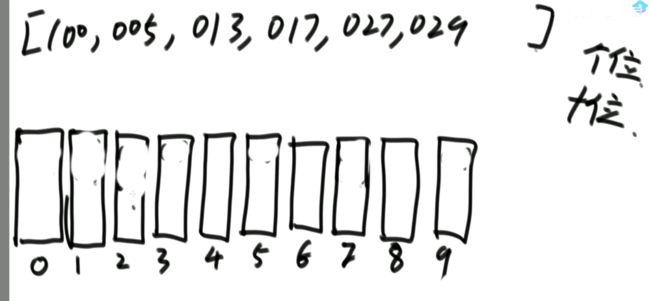
第七步，根据百位数字进桶再桶从左往右向数组里倒数字。

注意：
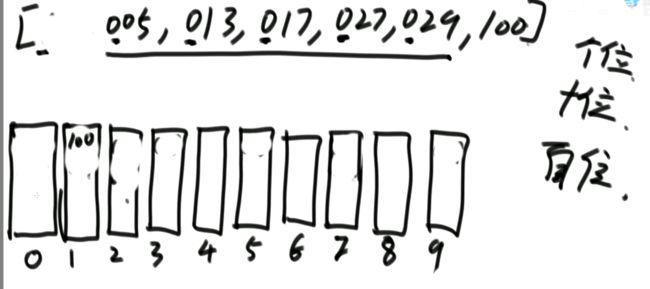
基于比较的排序，有更为广泛的用途，且时间复杂度极限是O(N*logN)；
做题过程中，除非有特殊声明，用到排序的要尽量使用基于比较的排序。

代码如下：

package class08;

import java.util.Arrays;

public class Code04_RadixSort {

	// only for no-negative value
	public static void radixSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		radixSort(arr, 0, arr.length - 1, maxbits(arr));
	}

	public static int maxbits(int[] arr) {
		int max = Integer.MIN_VALUE;
		for (int i = 0; i < arr.length; i++) {
			max = Math.max(max, arr[i]);
		}
		int res = 0;
		while (max != 0) {
			res++;
			max /= 10;
		}
		return res;
	}

	// arr[L..R]排序  ,  最大值的十进制位数digit
	public static void radixSort(int[] arr, int L, int R, int digit) {
		// 10进制
		final int radix = 10;
		int i = 0, j = 0;
		// 有多少个数准备多少个辅助空间
		int[] help = new int[R - L + 1];
		for (int d = 1; d <= digit; d++) { // 有多少位就进出几次
			// 10个空间
		    // count[0] 当前位(d位)是0的数字有多少个
			// count[1] 当前位(d位)是(0和1)的数字有多少个
			// count[2] 当前位(d位)是(0、1和2)的数字有多少个
			// count[i] 当前位(d位)是(0~i)的数字有多少个
			int[] count = new int[radix]; // count[0..9]
			for (i = L; i <= R; i++) {
				// 103  1   3
				// 209  1   9
				j = getDigit(arr[i], d);
				count[j]++;
			}
			for (i = 1; i < radix; i++) {
				count[i] = count[i] + count[i - 1];
			}
			for (i = R; i >= L; i--) {
				j = getDigit(arr[i], d);
				help[count[j] - 1] = arr[i];
				count[j]--;
			}
			for (i = L, j = 0; i <= R; i++, j++) {
				arr[i] = help[j];
			}
		}
	}

	public static int getDigit(int x, int d) {
		return ((x / ((int) Math.pow(10, d - 1))) % 10);
	}

	// for test
	public static void comparator(int[] arr) {
		Arrays.sort(arr);
	}

	// for test
	public static int[] generateRandomArray(int maxSize, int maxValue) {
		int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) ((maxValue + 1) * Math.random());
		}
		return arr;
	}

	// for test
	public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			res[i] = arr[i];
		}
		return res;
	}

	// for test
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

	// for test
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// for test
	public static void main(String[] args) {
		int testTime = 500000;
		int maxSize = 100;
		int maxValue = 100000;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue);
			int[] arr2 = copyArray(arr1);
			radixSort(arr1);
			comparator(arr2);
			if (!isEqual(arr1, arr2)) {
				succeed = false;
				printArray(arr1);
				printArray(arr2);
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");

		int[] arr = generateRandomArray(maxSize, maxValue);
		printArray(arr);
		radixSort(arr);
		printArray(arr);

	}

}

注意：代码中并没有准备10个队列，10个桶。如果实在搞不懂，下方解释----举例也搞不懂，那么搞10个队列也一样的。但是经典实现就是这样的。上述代码的时间复杂度是O(Nlog以10为底的N)，但是我们认为其时间复杂度是O(N)的，因为，使用基数排序的样本量N小。若样本量N非常大，我们应当明白其时间复杂度应是O(Nlog以10为底的N)

解释----举例1：一个数组arr[]：

按照基数排序：

并加工一下：count’中第二个数开始，假定位置为t，第t位置的数等于count数组中第t-1位置的数+第t位置的数。

对于count’ 的解释：个位数<=0的有0个。个位数<=1的有2个。个位数<=2的有4个。依此类推。
使用help[]数组：对原数组arr[]从右往左遍历。第一个数是302，原算法302应该是进2号桶且是最后被倒出的数字。
302个位数是2，又个位数<=2的有4个。所以302在3位置。

同时count’中相应的词频–

第二个数是41，应该在1号桶中最后一个倒出来，其个位是1。又个位数<=1的有两个，所以42在1位置。

同时count’中相应的词频–

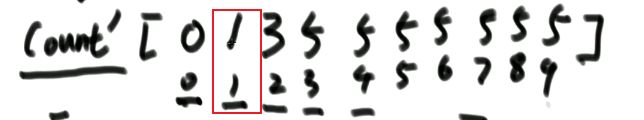
依此类推，最后情形如下：

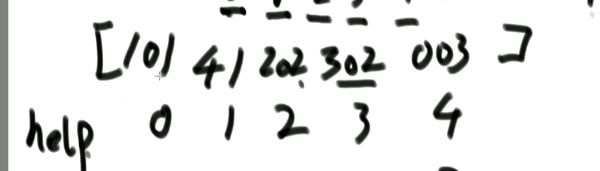
解释—举例2：假定一个原始数组arr[]：

基数排序原方法：根据个位加入桶中：

基数排序原方法：桶排序的结果arr’：

准备一个与arr[]数组等长的help[]数组

同时准备一个count[]数组：

然后我们根据arr[]数组的个位数对count计数：
下面这是arr[]数组中个位是0的出现了1次，个位是1的出现了2次，个位是2的出现了2次，个位是3的出现了1次。

我们之后把count加工成count’：count’中第二个数开始，假定位置为t，第t位置的数等于count数组中第t-1位置的数+第t位置的数。

从count’中我们可以知道：
arr[]数组中 个位数 <= 3的有6个；对应下标是0-5
arr[]数组中 个位数 <= 2的有5个；对应下标是0-4
arr[]数组中 个位数 <= 1的有3个；对应下标是0-2
arr[]数组中 个位数 <= 0的有1个；对应下标是0-0

接下来我们再看arr数组：从右往左看，第一个数为403。按照基数排序算法403是3号桶中最后出来的（如果在优先队列中，403应该最后一个出来，那么现在从count’中查看，从右往左读，那么403等于是最后一个），403个位数是3，其对应位置应在下标5中，如图的help数组。

同时count对应位置要–

同时arr[]数组中 个位数 <= 3的变为5个；对应下标变为0-4。到这里403数字已被去掉了。

接下来我们再看arr数组：从右往左看，第二个数为202。202根据基数排序是在个数为2的桶中，个数为2的桶中只有两个数012和202，且202作为位置为4的数，012作为位置为2的数，202应是后被倒出，即202应在下标较大的位置上和012相比
arr[]数组中 个位数 <= 2的有5个；对应下标是0-4
所以202应在位置为4的位置上。

同时count对应位置要–

同时arr[]数组中 个位数 <= 2的变为4个；对应下标变为0-3。到这里202数字已被去掉了。
依此类推…

疑问：为什么顺序是从右往左？
答：因为我们统计的是个数<=i的有几个，个数<=i的有几个只是划定了大致范围。比如各位数字<=3的有6个，位置在0-5之间。如果个位数字是3的数只有一个那么它就应该在5位置。

5.计数排序和基数排序

（1）一般来讲,计数排序要求,样本是整数,且范围比较窄
（2）一般来讲,基数排序要求,样本是10进制的正整数

一旦要求稍有升级,改写代价增加是显而易见的

6.排序算法的稳定性

稳定性是指同样大小的样本再排序之后不会改变相对次序
对基础类型来说，稳定性毫无意义
对非基础类型来说，稳定性有重要意义
有些排序算法可以实现成稳定的，而有些排序算法无论如何都实现不成稳定的

基础类型按值传递的所有东西谈稳定性没有意义；按引用传递的谈稳定性很有意义。

排序算法对于处理相等时的态度就决定了是否具有稳定性。

实际意义：网站购货，第一选择商品价格从低到高排序；再选择产品好坏由好到差。如果具有稳定性的话，那么物美价廉的商品就应该排在前面。

选择排序–不具有稳定性：

解释：0 - N-1之间选一个最小值放到0位置，这一步就破坏了稳定性了。

举例：[5 5 5 5 5 5 1 5 5 5 5]
0 N-1

1和5互换，这就破坏了稳定性。

冒泡排序–具有稳定性：

解释：从0到N-1相邻之间比大小不断交换，大的往后去，第一轮结束就选出一个最大值到最后一个位置。第二轮选出第二大的值到倒数第二个位置。相等的时候并没有交换。

举例：[3 2 3 1 2 3]
0 N-1




上述为第一轮选出最大值到最后一个位置。

插入排序–具有稳定性：

解释：从0到N-1位置，第N-1位置的数不断和前面比较，若后面的数小于前面的数就交换，否则不交换。相等的时候并没有交换。

举例：[1 1 2 2 3 3 2]
0 N-1

归并排序–具有稳定性：

解释：左组和右组相等的时候，先拷贝右边的稳定性就会被破坏。求逆序对的时候稳定性就被破坏了，而归并排序和求小和时稳定性不会被破坏。

举例：[1 1 2 2 3 1 1 4 4]
左组为[1 1 2 2 3]，右组为[1 1 4 4]
指针左组到1，右组到1。先把左边的两个1放到数组中，然后是右边的两个1放到数组中。

快速排序—不具有稳定性

前面所述的快排1.0、快排2.0、快排3.0都不具有稳定性。

解释：patition的过程就是不具有稳定性。以num做划分值，小于num的在左边，等于num的在中间，大于num的在右边都不具有稳定性。

举例：
快排1.0：快排2.0、快排3.0省略，与此同。num=5

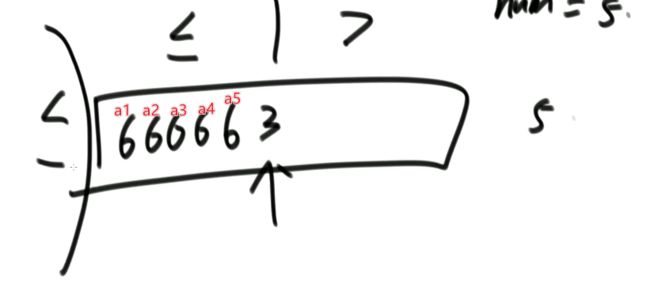
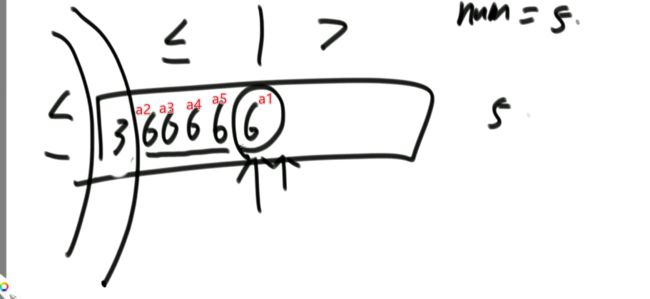
堆排序–不具有稳定性：

解释：它只关心保持为一个堆结构，稳定性根本就没关注。第一步把所有数变成一个大根堆结构，这第一步就不能保证稳定性了。

举例：

根据数组首先会变成上面这个样子，这不是大根堆结构，下面我们进行调整。

由上可知，它是不具有稳定性的。下面我们就不看了。

7.排序算法总结

注意：
桶排序是一种理念，计数排序和基数排序是对桶排序理念的实现。
基于比较的排序的时间复杂度极限也就是时间复杂度最小的意思。
少了一个希尔排序，因为它很少用，它也是简单插入排序的改进版本。可见ta人的博客
JAVA十大经典排序算法最强总结（含JAVA代码实现）

使用原则：
追求稳定性选归并排序；
追求额外空间的极致选堆排序；
追求速度的极致选快速排序。

8.常见的坑

（1）归并排序的额外空间复杂度可以变成O(1)，“归并排序 内部缓存法”，但是将变得不再稳定。
（2）“原地归并排序“是垃圾帖子，会让时间复杂度变成O(N^2)
（3）快速排序稳定性改进，“01 stable sort”，但是会对样本数据要求更多。

对于第1点，归并排序若想要额外空间复杂度变成O(1)，但变得不具有稳定性，倒不如用堆排序。

对于第2点，归并排序若想要额外空间复杂度变成O(1)，但会让时间复杂度变成O(N ^ 2)，倒不如用插入排序。

对于第3点，快速排序若想要稳定性，但是对样本数据要求更多，倒不如用桶排序。

上述问题是论文“ 0 1 stable sort”中的内容。水平高了再去看也不迟，水平低不合适。

解释：奇数放左边，偶数放右边，是一个 0 1标准的patition过程。
奇数和偶数之间原始的相对次序不变，即具有稳定性。
时间复杂度是O(N)，额外空间复杂度是O(1)

上述要求能实现，但是数组里面的数需要像桶排序一样有一个限制才可能实现。

快速排序的partition是小于等于一个数放左边，大于一个数放右边。这是不是什么就是什么的要求，所以这就是0 1标准。而快速排序的partition过程是做不到稳定性的。所以说上述奇数放左边，偶数放右边能具有稳定性这是不可能的！

9.工程上对排序的改进

（1）稳定性的考虑
（2）充分利用O(N * logN)和O(N ^ 2)排序各自的优势

Java中系统提供的排序：Arrays.sort()方法。系统提供的排序方法在底层非常的复杂，把多种排序算法的优势结合起来的一种综合排序。若你想要排序一个东西，它可能会先给你做一个反射，会查看你想要排序的东西是按值传递还是按引用传递的。如果是按值传递的会给你使用快速排序；如果是按引用传递的会给你使用归并排序，这是考虑到稳定性。若需要排序的全是基础类型，那么稳定性对你而言是没用的，既然如此，就调用最快的快速排序。若需要排序的有非基础类型，按引用传递的，系统不确定你是否需要稳定性，那么系统会使用归并排序，保持稳定性。

如图，快速排序中有时增加一个if，不够60个数使用插入排序然后返回，不往下进行二分这样做是为什么？
因为快速排序，归并排序，桶排序在调度上是非常优秀的，所以时间复杂度是O(N * logN)，然而其常数项是比较大的，当样本量小的时候，考虑到省略掉的常数项其时间复杂度就高了。而插入排序是调度上不优秀，所以时间复杂度是O(N ^ 2)，然而其常数项是比较小的。因此上图在快速排序中添加了一个当样本量很小的时候调用插入排序的操作。同时上述操作并不会增加时间复杂度，也使得样本量小时快速排序会变得更优。

六、链表相关面试题

1.链表问题

面试时链表解题的方法论
（1）对于笔试,不用太在乎空间复杂度,一切为了时间复杂度
（2）对于面试,时间复杂度依然放在第一位但是一定要找到空间最省的方法

2.链表面试题常用数据结构和技巧

（1）使用容器（哈希表、数组等）
（2）快慢指针

3.快慢指针的使用举例：

（1）输入链表头节点，奇数长度返回中点，偶数长度返回上中点
（2）输入链表头节点，奇数长度返回中点，偶数长度返回下中点
（3）输入链表头节点，奇数长度返回中点前一个，偶数长度返回上中点前一个
（4）输入链表头节点，奇数长度返回中点前一个，偶数长度返回下中点前一个

快慢指针的大逻辑：慢指针一次走一步，快指针一次走两步，快指针走完时，慢指针走到了中点位置。而对于上面四个问题，快慢指针存在一些细节的不同。

对于第一个问题的解析：

问题：输入链表头节点，奇数长度返回中点，偶数长度返回上中点
解法：

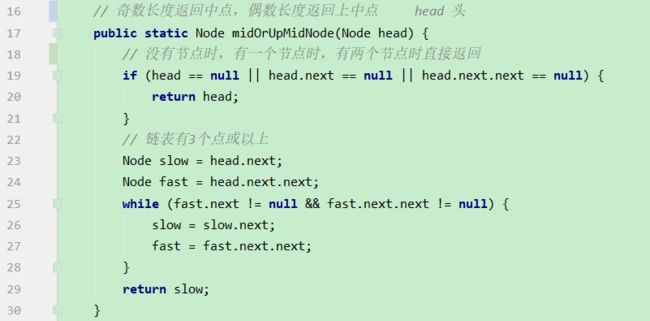
假设就3个节点：

代码最后返回的slow确实为奇数长度时的中点。其他奇数长度就不举例了。
假设有4个节点：

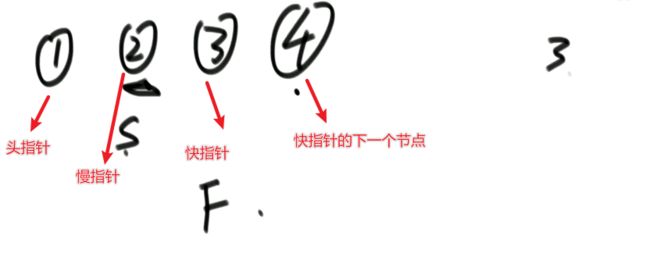
代码最后返回的slow确实为偶数长度时的上中点。其他偶数长度就不举例了。

对于第二个问题的解析：

问题：输入链表头节点，奇数长度返回中点，偶数长度返回下中点
解法：

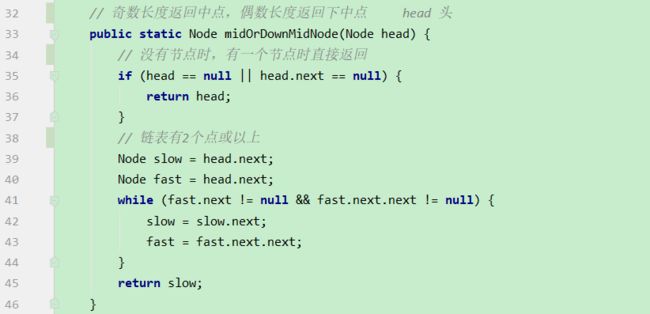
对于第三个问题的解析：

问题：输入链表头节点，奇数长度返回中点前一个，偶数长度返回上中点前一个
解法：

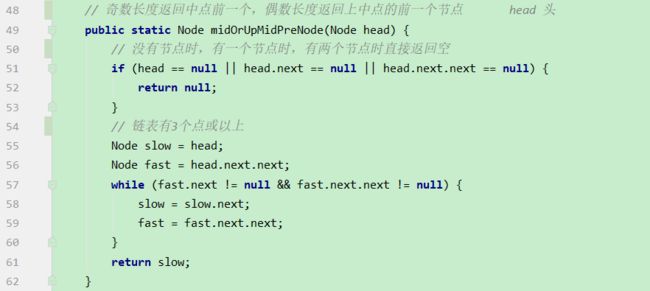
对于第四个问题的解析：

问题：输入链表头节点，奇数长度返回中点前一个，偶数长度返回下中点前一个
解法：

上述四个问题的全部代码和验证：
验证的方法其实也是上述四个问题的解决，只是方法简单，我们把它们用来验证上面的解法。

package class09;

import java.util.ArrayList;

public class Code01_LinkedListMid {

	public static class Node {
		public int value;
		public Node next;

		public Node(int v) {
			value = v;
		}
	}

	// 奇数长度返回中点，偶数长度返回上中点		head 头
	public static Node midOrUpMidNode(Node head) {
		// 没有节点时，有一个节点时，有两个节点时直接返回头节点
		if (head == null || head.next == null || head.next.next == null) {
			return head;
		}
		// 链表有3个点或以上
		Node slow = head.next;
		Node fast = head.next.next;
		while (fast.next != null && fast.next.next != null) {
			slow = slow.next;
			fast = fast.next.next;
		}
		return slow;
	}

	// 奇数长度返回中点，偶数长度返回下中点		head 头
	public static Node midOrDownMidNode(Node head) {
		// 没有节点时，有一个节点时直接返回头节点
		if (head == null || head.next == null) {
			return head;
		}
		// 链表有2个点或以上
		Node slow = head.next;
		Node fast = head.next;
		while (fast.next != null && fast.next.next != null) {
			slow = slow.next;
			fast = fast.next.next;
		}
		return slow;
	}

	// 奇数长度返回中点前一个，偶数长度返回上中点的前一个节点		head 头
	public static Node midOrUpMidPreNode(Node head) {
		// 没有节点时，有一个节点时，有两个节点时直接返回空
		if (head == null || head.next == null || head.next.next == null) {
			return null;
		}
		// 链表有3个点或以上
		Node slow = head;
		Node fast = head.next.next;
		while (fast.next != null && fast.next.next != null) {
			slow = slow.next;
			fast = fast.next.next;
		}
		return slow;
	}

	// 奇数长度返回中点前一个，偶数长度返回下中点的前一个节点		head 头
	public static Node midOrDownMidPreNode(Node head) {
		// 没有节点时，有一个节点时直接返回空
		if (head == null || head.next == null) {
			return null;
		}
		// 有两个节点时返回头节点
		if (head.next.next == null) {
			return head;
		}
		// 链表有3个点或以上
		Node slow = head;
		Node fast = head.next;
		while (fast.next != null && fast.next.next != null) {
			slow = slow.next;
			fast = fast.next.next;
		}
		return slow;
	}

	// 方法1的验证
	public static Node right1(Node head) {
		if (head == null) {
			return null;
		}
		Node cur = head;
		ArrayList<Node> arr = new ArrayList<>();
		while (cur != null) {
			arr.add(cur);
			cur = cur.next;
		}
		return arr.get((arr.size() - 1) / 2);
	}

	// 方法2的验证
	public static Node right2(Node head) {
		if (head == null) {
			return null;
		}
		Node cur = head;
		ArrayList<Node> arr = new ArrayList<>();
		while (cur != null) {
			arr.add(cur);
			cur = cur.next;
		}
		return arr.get(arr.size() / 2);
	}

	// 方法3的验证
	public static Node right3(Node head) {
		if (head == null || head.next == null || head.next.next == null) {
			return null;
		}
		Node cur = head;
		ArrayList<Node> arr = new ArrayList<>();
		while (cur != null) {
			arr.add(cur);
			cur = cur.next;
		}
		return arr.get((arr.size() - 3) / 2);
	}

	// 方法4的验证
	public static Node right4(Node head) {
		if (head == null || head.next == null) {
			return null;
		}
		Node cur = head;
		ArrayList<Node> arr = new ArrayList<>();
		while (cur != null) {
			arr.add(cur);
			cur = cur.next;
		}
		return arr.get((arr.size() - 2) / 2);
	}

	public static void main(String[] args) {
		Node test = null;
		test = new Node(0);
		test.next = new Node(1);
		test.next.next = new Node(2);
		test.next.next.next = new Node(3);
		test.next.next.next.next = new Node(4);
		test.next.next.next.next.next = new Node(5);
		test.next.next.next.next.next.next = new Node(6);
		test.next.next.next.next.next.next.next = new Node(7);
		test.next.next.next.next.next.next.next.next = new Node(8);

		Node ans1 = null;
		Node ans2 = null;

		ans1 = midOrUpMidNode(test);
		ans2 = right1(test);
		System.out.println(ans1 != null ? ans1.value : "无");
		System.out.println(ans2 != null ? ans2.value : "无");

		ans1 = midOrDownMidNode(test);
		ans2 = right2(test);
		System.out.println(ans1 != null ? ans1.value : "无");
		System.out.println(ans2 != null ? ans2.value : "无");

		ans1 = midOrUpMidPreNode(test);
		ans2 = right3(test);
		System.out.println(ans1 != null ? ans1.value : "无");
		System.out.println(ans2 != null ? ans2.value : "无");

		ans1 = midOrDownMidPreNode(test);
		ans2 = right4(test);
		System.out.println(ans1 != null ? ans1.value : "无");
		System.out.println(ans2 != null ? ans2.value : "无");

	}

}

4.常见面试题1

给定一个单链表的头节点head,请判断该链表是否为回文结构。
（1）栈方法特别简单（笔试用）
（2）改原链表的方法就需要注意边界了（面试用）

回文：从左向右看和从右向左看都一样。如字符串“12321”，“abcba”

链表回文结构：

解法1：把链表的值依次遍历放入到栈中。栈中的数据再依次弹出并与链表比较。

代码如下：

    // need n extra space
	public static boolean isPalindrome1(Node head) {
		Stack<Node> stack = new Stack<Node>();
		Node cur = head;
		while (cur != null) {
			stack.push(cur);
			cur = cur.next;
		}
		while (head != null) {
			if (head.value != stack.pop().value) {
				return false;
			}
			head = head.next;
		}
		return true;
	}

解法2—快慢指针：再利用少一点的空间

快慢指针定位到中点位置。奇数位置定位到中点，偶数位置定位到上中点。把中点位置后面的依次压入栈中。栈中存放的是右半部的逆序。

之后栈里弹出一个元素，链表拿一个节点出来，二者对比，直到栈里没元素为止。若直到栈里元素全部弹完后比对都相等，那么此链表就是回文结构。

上述操作就等同于把链表看作一个线段，从中点折过来。

代码如下：

 // need n/2 extra space
	public static boolean isPalindrome2(Node head) {
		if (head == null || head.next == null) {
			return true;
		}
		Node right = head.next;
		Node cur = head;
		while (cur.next != null && cur.next.next != null) {
			right = right.next;
			cur = cur.next.next;
		}
		Stack<Node> stack = new Stack<Node>();
		while (right != null) {
			stack.push(right);
			right = right.next;
		}
		while (!stack.isEmpty()) {
			if (head.value != stack.pop().value) {
				return false;
			}
			head = head.next;
		}
		return true;
	}

还有更优解：

奇数个时：

我们把右边的1的指针原本指向null的改为指向2；右边的2的指针原本指向右边的1的改为指向3；3原本指向右边的2的改为指向null。

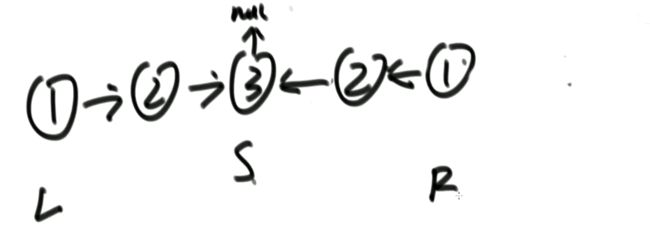
然后左指针L向右走，右指针R向左走，二者对比。 如果一路为true，那么就是回文结构，在返回true之前要先把指针给改为原来的样子。
偶数个时：

L和R指针不断移动，当某个指针下一个指向为null时就可以停了。 如果一路为true，那么就是回文结构，在返回true之前要先把指针给改为原来的样子。

代码如下：

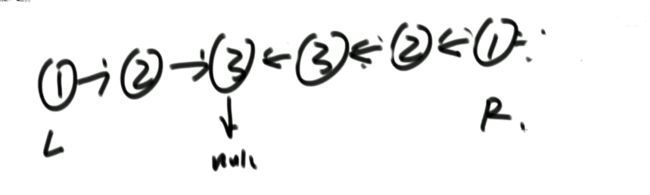
  // need O(1) extra space
	public static boolean isPalindrome3(Node head) {
		if (head == null || head.next == null) {
			return true;
		}
		Node n1 = head;		// 慢指针
		Node n2 = head;		// 快指针
		while (n2.next != null && n2.next.next != null) { // find mid node
			n1 = n1.next; // n1 -> mid
			n2 = n2.next.next; // n2 -> end
		}
		// n1 中点
		
		
		n2 = n1.next; // n2 -> right part first node
		n1.next = null; // mid.next -> null
		Node n3 = null;
		while (n2 != null) { // right part convert
			n3 = n2.next; // n3 -> save next node
			n2.next = n1; // next of right node convert
			n1 = n2; // n1 move
			n2 = n3; // n2 move
		}

		n3 = n1; // n3 -> save last node 最后还要把链表指针恢复原样，所以记录一下最右边的位置
		n2 = head;// n2 -> left first node
		boolean res = true;
		while (n1 != null && n2 != null) { // check palindrome
			if (n1.value != n2.value) {
				res = false;
				break;
			}
			n1 = n1.next; // left to mid
			n2 = n2.next; // right to mid
		}
		n1 = n3.next;
		n3.next = null;
		// 链表指针恢复原样
		while (n1 != null) { // recover list
			n2 = n1.next;
			n1.next = n3;
			n3 = n1;
			n1 = n2;
		}
		return res;
	}

上述三种方式的全部代码如下：

package class09;

import java.util.Stack;

public class Code02_IsPalindromeList {

	public static class Node {
		public int value;
		public Node next;

		public Node(int data) {
			this.value = data;
		}
	}

	// need n extra space
	public static boolean isPalindrome1(Node head) {
		Stack<Node> stack = new Stack<Node>();
		Node cur = head;
		while (cur != null) {
			stack.push(cur);
			cur = cur.next;
		}
		while (head != null) {
			if (head.value != stack.pop().value) {
				return false;
			}
			head = head.next;
		}
		return true;
	}

	// need n/2 extra space
	public static boolean isPalindrome2(Node head) {
		if (head == null || head.next == null) {
			return true;
		}
		Node right = head.next;
		Node cur = head;
		while (cur.next != null && cur.next.next != null) {
			right = right.next;
			cur = cur.next.next;
		}
		Stack<Node> stack = new Stack<Node>();
		while (right != null) {
			stack.push(right);
			right = right.next;
		}
		while (!stack.isEmpty()) {
			if (head.value != stack.pop().value) {
				return false;
			}
			head = head.next;
		}
		return true;
	}

	// need O(1) extra space
	public static boolean isPalindrome3(Node head) {
		if (head == null || head.next == null) {
			return true;
		}
		Node n1 = head;		// 慢指针
		Node n2 = head;		// 快指针
		while (n2.next != null && n2.next.next != null) { // find mid node
			n1 = n1.next; // n1 -> mid
			n2 = n2.next.next; // n2 -> end
		}
		// n1 中点
		
		
		n2 = n1.next; // n2 -> right part first node
		n1.next = null; // mid.next -> null
		Node n3 = null;
		while (n2 != null) { // right part convert
			n3 = n2.next; // n3 -> save next node
			n2.next = n1; // next of right node convert
			n1 = n2; // n1 move
			n2 = n3; // n2 move
		}

		n3 = n1; // n3 -> save last node 最后还要把链表指针恢复原样，所以记录一下最右边的位置
		n2 = head;// n2 -> left first node
		boolean res = true;
		while (n1 != null && n2 != null) { // check palindrome
			if (n1.value != n2.value) {
				res = false;
				break;
			}
			n1 = n1.next; // left to mid
			n2 = n2.next; // right to mid
		}
		n1 = n3.next;
		n3.next = null;
		// 链表指针恢复原样
		while (n1 != null) { // recover list
			n2 = n1.next;
			n1.next = n3;
			n3 = n1;
			n1 = n2;
		}
		return res;
	}

	public static void printLinkedList(Node node) {
		System.out.print("Linked List: ");
		while (node != null) {
			System.out.print(node.value + " ");
			node = node.next;
		}
		System.out.println();
	}

	public static void main(String[] args) {

		Node head = null;
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(2);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(1);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(2);
		head.next.next = new Node(3);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(2);
		head.next.next = new Node(1);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(2);
		head.next.next = new Node(3);
		head.next.next.next = new Node(1);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(2);
		head.next.next = new Node(2);
		head.next.next.next = new Node(1);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

		head = new Node(1);
		head.next = new Node(2);
		head.next.next = new Node(3);
		head.next.next.next = new Node(2);
		head.next.next.next.next = new Node(1);
		printLinkedList(head);
		System.out.print(isPalindrome1(head) + " | ");
		System.out.print(isPalindrome2(head) + " | ");
		System.out.println(isPalindrome3(head) + " | ");
		printLinkedList(head);
		System.out.println("=========================");

	}

}

5.常见面试题2

将单向链表按某值划分成左边小、中间相等、右边大的形式
（1）把链表放入数组里，在数组上做 partition(笔试用)
（2）分成小、中、大三部分，再把各个部分之间串起来(面试用)

举例：

解法1—链表放入数组中：
方法简单，直接看代码就可以了。

解法2—分成三个部分，再把各个部分之间穿起来：
创建6个指针。小于区的头sH和小于区的尾sT；等于区的头eH和等于区的尾eT；大于区的头mH（bH）和大于区的尾mT（bT）
举例：num=3

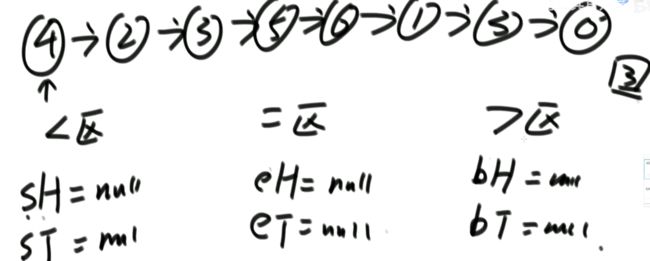
第一个节点4 ，是大于3的，把4发到>区，所以此时>区的头和尾都是4，再把指针断掉，由于我们用了变量记录节点4，所以我们不用担心节点会丢失。

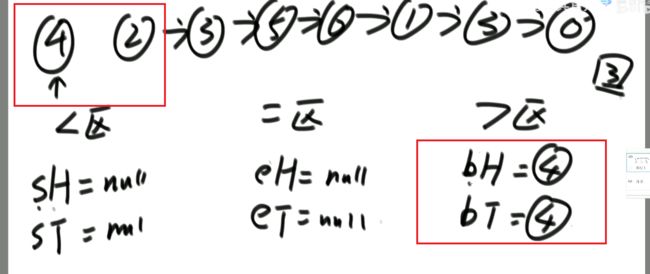
第二个节点2，是小于3的，把2发到<区，所以此时<区的头和尾都是2，再把指针断掉，由于我们用了变量记录节点2，所以我们不用担心节点会丢失。

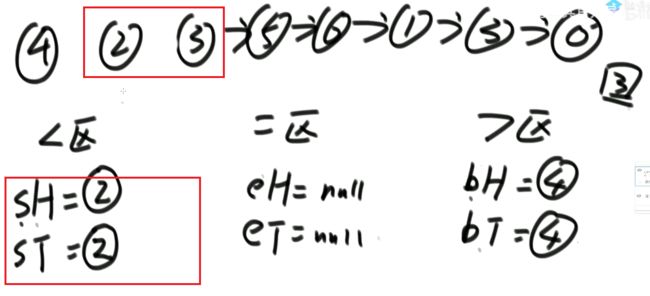
第三个节点3，是等于3的，把3发到=区，所以此时=区的头和尾都是3，再把指针断掉，由于我们用了变量记录节点3，所以我们不用担心节点会丢失。

第四个节点5，是大于3的，把5发到>区，又>区的尾巴是4，5覆盖掉尾巴4。4已经指向了5

第五个节点6，是大于3的，把6发到>区。再把6串到5下面。4串向5，5串向6.但我们只记录两个地址，一个头一个尾。再把指针断掉。

依此类推…最后，头尾相连，返回<区的头。

代码如下：下面的是两种解法的代码

package class09;

public class Code03_SmallerEqualBigger {

	public static class Node {
		public int value;
		public Node next;

		public Node(int data) {
			this.value = data;
		}
	}

	// 链表放入数组中的方法
	public static Node listPartition1(Node head, int pivot) {
		if (head == null) {
			return head;
		}
		Node cur = head;
		int i = 0;
		while (cur != null) {
			i++;
			cur = cur.next;
		}
		Node[] nodeArr = new Node[i];
		i = 0;
		cur = head;
		for (i = 0; i != nodeArr.length; i++) {
			nodeArr[i] = cur;
			cur = cur.next;
		}
		arrPartition(nodeArr, pivot);
		for (i = 1; i != nodeArr.length; i++) {
			nodeArr[i - 1].next = nodeArr[i];
		}
		nodeArr[i - 1].next = null;
		return nodeArr[0];
	}

	public static void arrPartition(Node[] nodeArr, int pivot) {
		int small = -1;
		int big = nodeArr.length;
		int index = 0;
		while (index != big) {
			if (nodeArr[index].value < pivot) {
				swap(nodeArr, ++small, index++);
			} else if (nodeArr[index].value == pivot) {
				index++;
			} else {
				swap(nodeArr, --big, index);
			}
		}
	}

	public static void swap(Node[] nodeArr, int a, int b) {
		Node tmp = nodeArr[a];
		nodeArr[a] = nodeArr[b];
		nodeArr[b] = tmp;
	}

	// 分成三个部分，再把各个部分之间穿起来的方法
	public static Node listPartition2(Node head, int pivot) {
		Node sH = null; // small head
		Node sT = null; // small tail
		Node eH = null; // equal head
		Node eT = null; // equal tail
		Node mH = null; // big head
		Node mT = null; // big tail
		Node next = null; // save next node
		// every node distributed to three lists
		while (head != null) {
			next =