数据结构-笔记总结
文章目录
- 前言
- 1 学习思路
-
- 1.1 常使用画图工具
- 1.2 以处理实际应用问题为目标
- 2 数据结构
-
- 2.1 基本概念
-
- 2.1.1什么是数据
- 2.1.2 数据元素、数据项
- 2.2 数据结构三要素
- 2.3 数据结构三要素展开的内容
-
- 2.3.1 线性结构还可以细分
- 3 算法
-
- 3.1 算法中推导大O阶的方法
- 3.2 常见的时间复杂度
- 4 树
-
- 4.1 定义
-
- 4.1.1 什么是树
- 4.1.2 树内容总览图
- 4.1.3 树子树的概念
- 4.1.4 度数的概念
- 4.1.5 节点间的关系
- 4.2 二叉树
-
- 4.2.1 二叉树的一些性质
-
- 4.2.1.2 二叉树遍历
- 4.2.2 完全二叉树
- 4.2.3 满二叉树
- 4.2.4 树的算法
-
- 4.2.4.1 什么是赫夫曼树?
- 5 线性表
-
- 5.1 线性表的顺序存储(顺序表,seqlist)
-
- 5.1.1 顺序表的动态分配(malloc)
-
- 5.1.1.1 需要注意的地方
- 5.1.2 顺序表的静态分配
-
- 5.1.2.1 需要注意的地方
- 5.2 线性表的链式存储(链表、linklist)
-
- 5.2.1 单链表
-
- 5.2.1.1 单链表需要注意的地方
- 5.2.3 双向链表
-
- 5.2.3.1 双向链表需要注意的地方
- 5.2.4 循环链表
-
-
- 5.2.4.1 循环链表需要注意的地方
- 循环链表总结:
-
- 5.2.5 双向循环链表
-
- 5.2.5.1 需要注意的地方
- 5.3 栈
-
- 5.3.1 顺序栈
-
- 5.3.1.1 需要注意的地方
- 5.3.2 链式栈
-
- 5.3.1.2 需要注意的地方
- 5.4 队列
-
- 5.4.1 顺序队列(队列的顺序存储方式)
- 5.4.2 链式队列
-
- 5.4.2.1 需要注意的地方
- 6 图
- 总结
前言
如今,处理非数值运算问题占用了计算机90%的时间。这类的数据结构更为复杂,因此需要设计出适合的数据结构尤为重要。数据结构是我来到成都华清远见结构学习的第三门课程,这门课程属于步入计算机代码编程最为核心的课程之一,做好笔记以便以后复习。
1 学习思路
1.1 常使用画图工具
常使用画图工具(推荐使用pointofix这个软件)画图来模拟具体的过程,模拟后进行写代码。
1.2 以处理实际应用问题为目标
除了使用数据结构实现基本的操作以外(初始化、插入数据、删除数据等等操作),更重要的还需要解决实际问题。比如实现约瑟夫环、推箱子游戏的撤销操作等等应用。
2 数据结构
数据结构是什么?:相互之间存在一种或多种特定关系的数据元素的集合。
2.1 基本概念
2.1.1什么是数据
2.1.2 数据元素、数据项

数据元素举例:比如下图的排队信息的一波顾客就是数据元素。
数据项 举例:而顾客的号数、取号时间等就是数据项。
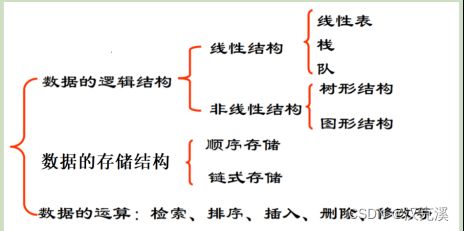
2.2 数据结构三要素
逻辑结构、存储结构(又可以叫物理结构)、操作统称为数据结构的三要素。

2.3 数据结构三要素展开的内容
2.3.1 线性结构还可以细分
线性结构的种类比较多,按照存储结构可以分为 ①:顺序存储结构 ②:链式存储结构。
链式存储结构又可以分为:①:单链表 ②:循环链表 ③:双向链表 ④:静态链表。
3 算法
3.1 算法中推导大O阶的方法
大致分为3步,如下图

如以下代码:按照上面第一个步骤推导出:执行总次数为:2n+1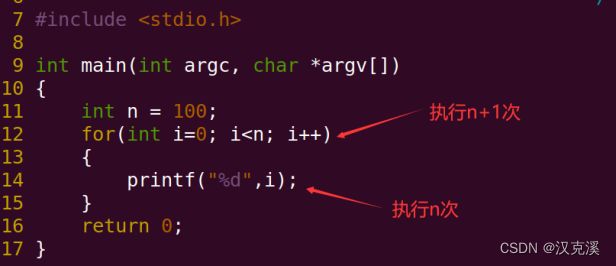
第二个步骤:保留最高项后为2n
第三个步骤:如果最高阶存在且不是1,则去掉系数。去掉系数后为n
则推导出上面代码的时间复杂度T(n) = O(n)
3.2 常见的时间复杂度
常见的时间复杂度有以下几种:

各种时间复杂度所花费的时间从小到大以此是:

由于n^2后的时间复杂度花费的时间过长,通常情况下不讨论。
4 树
4.1 定义
4.1.1 什么是树
定义:n个节点(n>=0)的有限集。n=0时,为空树。当n大于0时,为非空树。
非空树特性:
(1)有且仅有一个特定的称为根(Root) 的结点;
(2)当n>1时,其余结点可分为m (m>0)个互不相交的有限集T1、 T2、… Tm, 其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
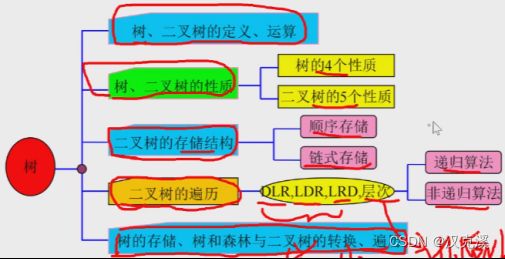
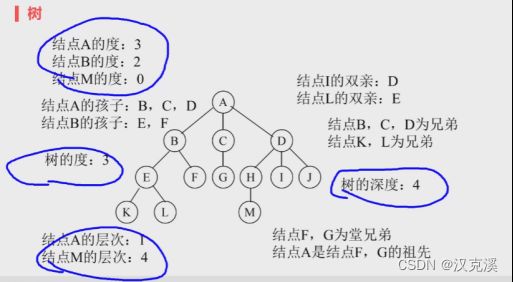
4.1.2 树内容总览图
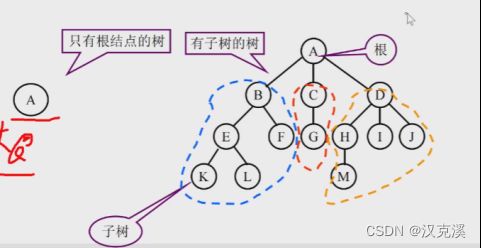
4.1.3 树子树的概念
4.1.4 度数的概念
一个节点子树的个数称为该节点的度数。
一个树的度数:指的是指该树中节点最大的度数。
度数为零:被称为树叶或者终端节点。
度数不为零:分支节点。 除了根节点以外的节点称为内部节点。
内部节点:除了树叶和树根的节点。
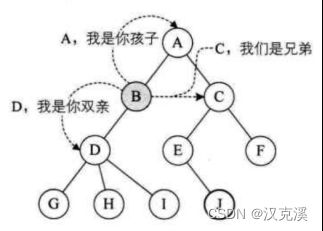
4.1.5 节点间的关系
4.2 二叉树
由于树有很多情况,所以这里单独讨论二叉树。
4.2.1 二叉树的一些性质
①:一个二叉树第i层,最多有:2i-1 个节点,比如第一层最多有1(20)个,第二层最多有2(21)个,第三层最多有4(22)个。
②:一个深度为k的二叉树,所有节点数量之和,最多为2k-1
4.2.1.2 二叉树遍历
有三种常见的遍历方法 :
先序:根、左、右
中序:左、根、右
后序:左、右、根
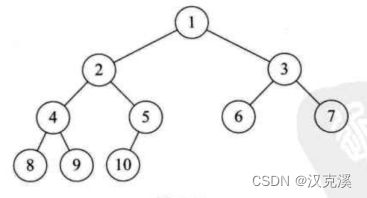
4.2.2 完全二叉树
4.2.3 满二叉树
节点数量为2k-1的树,k为深度。
4.2.4 树的算法
4.2.4.1 什么是赫夫曼树?
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
例如:假设有权值大小为1、2、3、4、5、6的节点,画出最优的二叉树。结果如下。
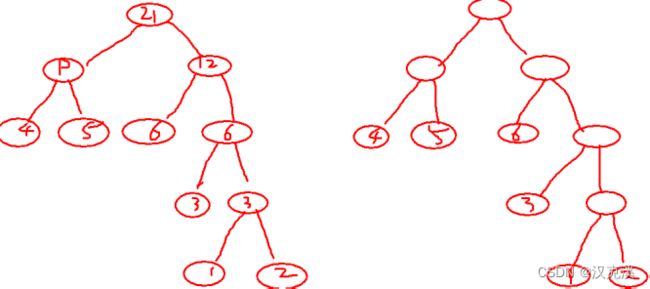
思路总结:先对权值进行排序,排序后取前两个开始作为树叶往上画,比如上个例子求和之后为3,然后用3在进入到原始队列中排序(已经用过了的权值除外),再然后取最小两个数进行求和。
5 线性表
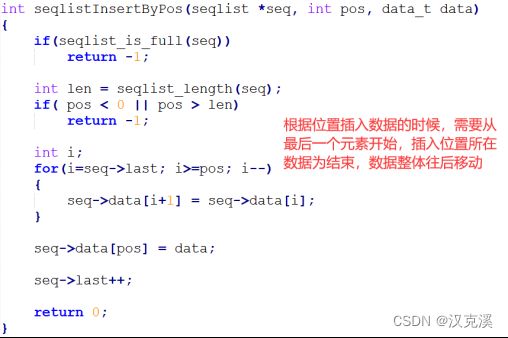
5.1 线性表的顺序存储(顺序表,seqlist)
顺序表就是数组。
结构体如下(last指的是最后一个有效元素的下标)
#define SIZE 100
typedef struct list{
int data[SIZE];
int last;
}seqlist;
5.1.1 顺序表的动态分配(malloc)
5.1.1.1 需要注意的地方
5.1.2 顺序表的静态分配
5.1.2.1 需要注意的地方
①:不使用malloc初始化,因此malloc初始化功能可以注释掉,下面使用了#if 0注释了代码。

②:main函数中,直接给结构体赋值进行初始化
seqlist seq = {{0}, -1};
③:其他函数代码基本与动态分配的顺序表类似,调用函数的时候需要传seq的地址。
比如:
seqlist_dispaly(&seq);
④:因为不是从堆区开辟空间,所以销毁功能也不需要了。
#if 0
seqlist_destroy(&seq);
#endif
5.2 线性表的链式存储(链表、linklist)
线性表,在存储方式上采用链式存储。
5.2.1 单链表
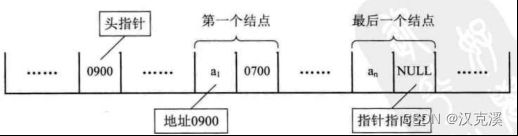
结构体
typedef struct node{
data_t data;
struct node *next;
}linklist;
5.2.1.1 单链表需要注意的地方
①:清空链表,需要free有效节点。q不断去记录下一个节点,p用来记录当前需要free的节点。
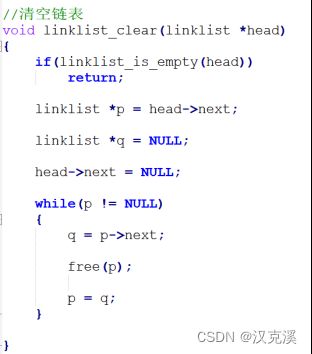
②:销毁链表,销毁链表前,需要先将所有有效节点free掉。然后free头结点。

③:面试题中有这样的题目:将一个链表逆序排序。原理是将一个一个节点拆开,然后使用头插法。这样重新插入所有节点后,再打印就是逆序的结果。

5.2.2 静态链表(主要学习其中的思想)
早期的编程语言,比如basic、fortran没有指针,于是用数组来代替指针,来描述链表。
对于线性链表,也可用一维数组来进行描述。这种描述方法便于在没有指针类型的高级程序设计语言中使用链表结构。
5.2.3 双向链表
结构体
typedef int data_t;
typedef struct node{
data_t data;
struct node *next; //保存下一个结点的地址
struct node *prior; //保存上一个结点的地址
}dlinklist;
5.2.3.1 双向链表需要注意的地方
①:在中间插入元素需要做四部操作,如下图(请注意操作顺序,总结就是先链接新节点、后断开)。
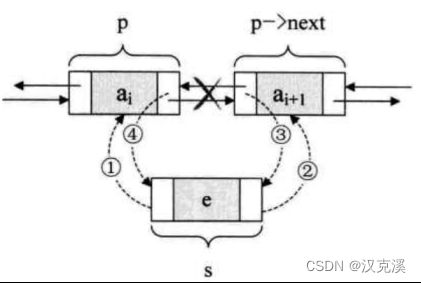
②:在执行删除操作的时候,如果是删除中间则需要把当前节点的下一个节点的prior指向当前节点。如果是删除末尾的节点,则不需要做这一步操作。如下图代码。
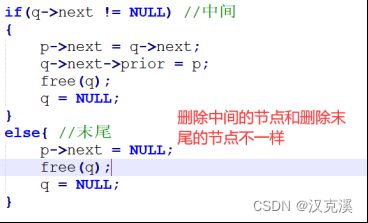
③:链表的逆序。基本原理还是头插法。双向链表需要注意的是,除了第一个节点只需要链接两个指针外,其余节点需要连三个指针。如下图代码。

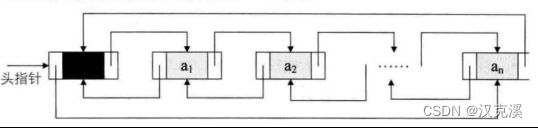
5.2.4 循环链表
结构体
typedef struct node{
data_t data;
struct node *next;
}linklist;
5.2.4.1 循环链表需要注意的地方
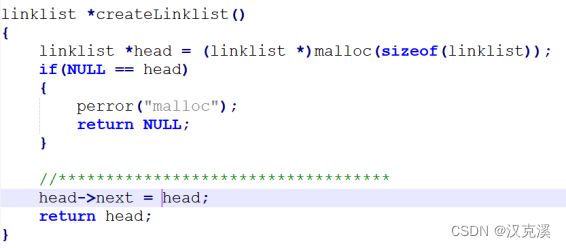
①:初始化的时候,头指针的next指向头节点地址。
④:循环里面的判断条件需要修改成类似于:while(p != head)
循环链表总结:
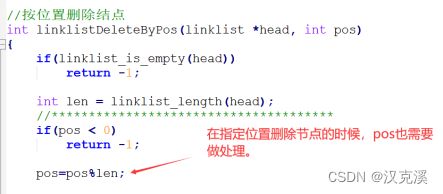
①:用到了pos来进行操作的,需要将pos进行取余处理。
②:循环里面的判断条件,需要又以前的while(p != null)调整为while(p != head)
③:涉及计pos位置是否合理的地方不再需要pos与链表长度相比较。
5.2.5 双向循环链表
结构体
typedef struct node{
data_t data;
struct node *next; //保存下一个结点的地址
struct node *prior; //保存上一个结点的地址
}dlinklist;
5.2.5.1 需要注意的地方
①:初始化的时候,next、prior指针都指向head的地址。
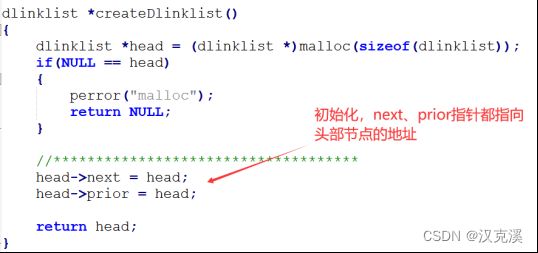
②:其余特性可以参考双向链表和循环链表需要注意的地方。
5.3 栈
5.3.1 顺序栈
结构体:
#define SIZE 100
typedef int data_t;
typedef struct list{
data_t data[SIZE];
int top; //栈顶数据的下标
}seqstack;
5.3.1.1 需要注意的地方
5.3.2 链式栈
结构体:
typedef struct node{
data_t data;
struct node *next;
}lstack;
5.3.1.2 需要注意的地方
5.4 队列
5.4.1 顺序队列(队列的顺序存储方式)
结构体
#define SIZE 100
typedef int data_t;
typedef struct list{
data_t data[SIZE];
int front; //对头元素的下标 删除
int rear; //队尾元素的下标 插入
}squeue;
//还有内容,待补充
5.4.2 链式队列
front指向队头节点的前一个节点; rear指向队尾节点。
结构体
typedef int data_t;
typedef struct node{
data_t data;
struct node *next;
}linklist;
typedef struct list{
linklist *front; //队头结点的前一个结点
linklist *rear; //队尾结点
}lqueue;
5.4.2.1 需要注意的地方
①:初始化是这样的。
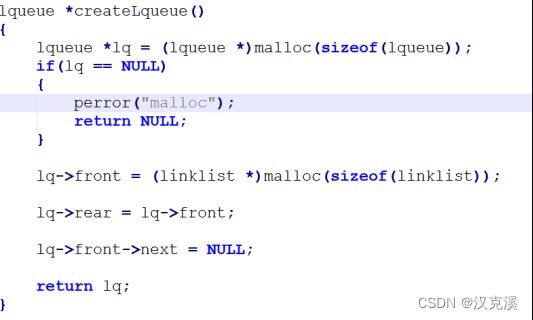
②:出队如果是出的最后一个元素,需要移动rear的位置。

6 图
图主要用于人工智能等方向。
笔记待更新…
总结
笔记主要涵盖了线性结构,比如顺序表、链式表、队列、栈等数据结构的特性,以及展示了其特性方面的代码。
树形、图形结构主要学习其理论。