计算机图形学14：三维图形的投影变换

作者：非妃是公主
专栏：《计算机图形学》
博客地址：https://blog.csdn.net/myf_666
个性签：顺境不惰，逆境不馁，以心制境，万事可成。——曾国藩

专栏推荐

专栏名称	专栏地址
软件工程	专栏——软件工程
计算机图形学	专栏——计算机图形学
操作系统	专栏——操作系统
软件测试	专栏——软件测试
机器学习	专栏——机器学习
数据库	专栏——数据库
算法	专栏——算法

专栏系列文章

文章名称	文章地址
直线生成算法(DDA算法)	计算机图形学01——DDA算法
中点BH算法绘制直线	计算机图形学02——中点BH算法
改进的中点BH算法	计算机图形学03——改进的中点BH算法
中点Bresenham画椭圆	计算机图形学04——中点BH绘制椭圆
中点BH算法绘制任意斜率直线	计算机图形学05——中点BH算法绘制任意斜率的直线
中点Bresenham画圆	计算机图形学06——中点BH算法画圆
有效边表法的多边形扫描转换	计算机图形学07——有效边表法绘制填充多边形
中点BH算法绘制抛物线 $100x=y^2$	计算机图形学08——中点BH绘制抛物线
二维观察之点的裁剪	计算机图形学09——二维观察之点裁剪
二维观察之线的裁剪	计算机图形学10——二维观察之线裁剪
二维观察之多边形的裁剪	计算机图形学11——二维观察之多边形裁剪
二维图形的几何变换	计算机图形学12——二维图形几何变换
三维图形的几何变换	计算机图形学13——三维图形几何变换
三维图形的投影变换	计算机图形学14——三维图形投影变换

序

计算机图形学（英语：computer graphics，缩写为CG）是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科，是计算机科学的一个分支领域，主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形，事实上同时包括了二维图形以及影像处理。

---

一、三维图形的投影变换

三维图形的投影变换可分为两类：平行投影和透视投影。

---

二、平行投影

平行投影可分为两类：正投影和斜投影。

---

1. 正投影

其中正投影中又可以分为：三视图和正轴测图。

---

Ⅰ. 三视图

① 主视图

主视图是逆着y轴方向去看，所以y轴的坐标为0，进而变化矩阵如下：

T z o x = [ 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 ]   T_{zox}=\begin{bmatrix} 1&0&0&0\\ 0&0&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}\ Tzox​= ​1000​0000​0010​0001​ ​ 

由于主视图已经落在了xoz平面上，所以不需要其它操作。
代码实现如下：

/// 

/// 将点转化为其次坐标
/// 
/// 点
/// 齐次坐标
Matrix vertex3D2qici(VERTEX3D vertex3D) {
	Matrix qiciVertex(4, 1);
	qiciVertex.matrix[0][0] = vertex3D.x;
	qiciVertex.matrix[1][0] = vertex3D.y;
	qiciVertex.matrix[2][0] = vertex3D.z;
	qiciVertex.matrix[3][0] = 1;
	return qiciVertex;
}

VERTEX3D qici2vertex3D(Matrix qici) {
	VERTEX3D res;
	res.x = qici.matrix[0][0];
	res.y = qici.matrix[1][0];
	res.z = qici.matrix[2][0];
	return res;
}

VERTEX3D mainViewTransform3D(VERTEX3D vertex3D) {
	Matrix qiciVertex = vertex3D2qici(vertex3D);

	Matrix transform;		 // 去掉y坐标变换矩阵
	transform.matrix[0][0] = 1;
	transform.matrix[1][1] = 0;
	transform.matrix[2][2] = 1;
	transform.matrix[3][3] = 1;

	Matrix qicires = dotMatrix(transform, qiciVertex);

	VERTEX3D res = qici2vertex3D(qicires);	 
	return res;
}

---

② 俯视图

俯视图逆着z轴的方向来看，因此需要将z轴上的坐标置为0，第一步变换矩阵如下：

T x o y = [ 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 ]   T_{xoy}=\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&0&0\\ 0&0&0&1\\ \end{bmatrix}\ Txoy​= ​1000​0100​0000​0001​ ​ 

同时由于最终要是的三个视图落在一个平面内(xoz平面)，因此还需要对视图进行旋转，使得俯视图绕着x轴旋转-90度，第二度变换矩阵如下：

T R x = [ 1 0 0 0 0 c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 ] = [ 1 0 0 0 0 0 1 0 0 − 1 0 0 0 0 0 1 ] T_{Rx}=\begin{bmatrix} 1&0&0&0\\ 0&cos\theta&-sin\theta&0\\ 0&sin\theta&cos\theta&0\\ 0&0&0&1\\ \end{bmatrix}=\begin{bmatrix} 1&0&0&0\\ 0&0&1&0\\ 0&-1&0&0\\ 0&0&0&1\\ \end{bmatrix} TRx​= ​1000​0cosθsinθ0​0−sinθcosθ0​0001​ ​= ​1000​00−10​0100​0001​ ​
此处 $\theta =-90^{\circ }$

最后还要将主视图和俯视图分开，保持一定间距，还要让俯视图向下平移一个单位向量 $-z_0$。

T T z = [ 1 0 0 0 0 1 0 0 0 0 1 − z 0 0 0 0 1 ] T_{Tz}=\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&-z_0\\ 0&0&0&1\\ \end{bmatrix} TTz​= ​1000​0100​0010​00−z0​1​ ​

所以总变换矩阵如下：

$$p^{\prime }=T_{Tz}\cdot T_{Rx}\cdot T_{xoy}\cdot p$$

VERTEX3D topViewTransform3D(VERTEX3D vertex3D) {
	Matrix qiciVertex = vertex3D2qici(vertex3D);

	Matrix transform1;		// 去掉z坐标变换矩阵
	transform1.matrix[0][0] = 1;
	transform1.matrix[1][1] = 1;
	transform1.matrix[2][2] = 0;
	transform1.matrix[3][3] = 1;

	Matrix qicitmp = dotMatrix(transform1, qiciVertex); // 去掉z坐标
	VERTEX3D tmp = qici2vertex3D(qicitmp);
	tmp = rotationForXTransform3D(tmp, -90);		// 沿x轴旋转90度
	tmp = transTransform3D(tmp, 0, 0, -100);		// 向下平移-1个单位
	return tmp;
}

---

③ 侧视图

侧视图为逆着x轴看，所以要将x方向的坐标置为0：

T y o z = [ 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] T_{yoz}=\begin{bmatrix} 0&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} Tyoz​= ​0000​0100​0010​0001​ ​

同理，为了与主视图画在一个平面内，使侧视面绕z轴旋转$90^{\circ }$，如下：

T R x = [ c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] = [ 0 − 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 ] T_{Rx}=\begin{bmatrix} cos\theta&-sin\theta&0&0\\ sin\theta&cos\theta&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}=\begin{bmatrix} 0&-1&0&0\\ 1&0&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} TRx​= ​cosθsinθ00​−sinθcosθ00​0010​0001​ ​= ​0100​−1000​0010​0001​ ​
然后与主视图有一定间距，向x轴负方向平移$-x_0$，如下：
T T x = [ 1 0 0 − x 0 0 1 0 0 0 0 1 0 0 0 0 1 ] T_{Tx}=\begin{bmatrix} 1&0&0&-x_0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} TTx​= ​1000​0100​0010​−x0​001​ ​

所以总变换矩阵如下：

$$p^{\prime }=T_{Tx}\cdot T_{Rz}\cdot T_{yoz}\cdot p$$

实现代码如下：

VERTEX3D sideViewTransform3D(VERTEX3D vertex3D) {
	Matrix qiciVertex = vertex3D2qici(vertex3D);

	Matrix transform1;		// 去掉x坐标变换矩阵
	transform1.matrix[0][0] = 0;
	transform1.matrix[1][1] = 1;
	transform1.matrix[2][2] = 1;
	transform1.matrix[3][3] = 1;

	Matrix qicitmp = dotMatrix(transform1, qiciVertex); // 去掉x坐标
	VERTEX3D tmp = qici2vertex3D(qicitmp);
	tmp = rotationForZTransform3D(tmp, 90);	// 沿x轴旋转90度
	tmp = transTransform3D(tmp, -100, 0, 0);		// 向x负方向平移-1个单位
	return tmp;
}

---

④ 三视图效果展示

测试效果代码：

void testThreeView() {
	VERTEX3D vertex3D_1 = { 100,100,100 };
	VERTEX3D vertex3D_2 = { 0,100,0 };
	VERTEX3D vertex3D_3 = { 200,100,0 };
	VERTEX3D vertex3D_4 = { 200,0,0 };

	// 主视图
	VERTEX3D res1 = mainViewTransform3D(vertex3D_1);
	VERTEX3D res2 = mainViewTransform3D(vertex3D_2);
	VERTEX3D res3 = mainViewTransform3D(vertex3D_3);
	VERTEX3D res4 = mainViewTransform3D(vertex3D_4);

	glBegin(GL_LINES);
	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res2.x, res2.z);

	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res3.x, res3.z);

	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res4.x, res4.z);

	glVertex2f(-res2.x, res2.z);
	glVertex2f(-res3.x, res3.z);

	glVertex2f(-res2.x, res2.z);
	glVertex2f(-res4.x, res4.z);

	glVertex2f(-res3.x, res3.z);
	glVertex2f(-res4.x, res4.z);
	glEnd();

	// 上视图
	res1 = topViewTransform3D(vertex3D_1);
	res2 = topViewTransform3D(vertex3D_2);
	res3 = topViewTransform3D(vertex3D_3);
	res4 = topViewTransform3D(vertex3D_4);

	glBegin(GL_LINES);
	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res2.x, res2.z);

	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res3.x, res3.z);

	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res4.x, res4.z);

	glVertex2f(-res2.x, res2.z);
	glVertex2f(-res3.x, res3.z);

	glVertex2f(-res2.x, res2.z);
	glVertex2f(-res4.x, res4.z);

	glVertex2f(-res3.x, res3.z);
	glVertex2f(-res4.x, res4.z);
	glEnd();

	// 侧视图
	res1 = sideViewTransform3D(vertex3D_1);
	res2 = sideViewTransform3D(vertex3D_2);
	res3 = sideViewTransform3D(vertex3D_3);
	res4 = sideViewTransform3D(vertex3D_4);

	glBegin(GL_LINES);
	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res2.x, res2.z);

	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res3.x, res3.z);

	glVertex2f(-res1.x, res1.z);
	glVertex2f(-res4.x, res4.z);

	glVertex2f(-res2.x, res2.z);
	glVertex2f(-res3.x, res3.z);

	glVertex2f(-res2.x, res2.z);
	glVertex2f(-res4.x, res4.z);

	glVertex2f(-res3.x, res3.z);
	glVertex2f(-res4.x, res4.z);
	glEnd();
	cout << res1.x << " " << res1.z << endl;
}

// 显示图形
void Display(void) {
	glClear(GL_COLOR_BUFFER_BIT);					//用当前背景色填充窗口
	// 此处需增加调用基本图形生成函数
	glColor3f(0.0f, 0.0f, 0.0f);			//设置当前的绘图颜色为红色
	glBegin(GL_LINES);
	glVertex2d(-400, 0);
	glVertex2d(400, 0);

	glVertex2d(0, 300);
	glVertex2d(0, -300);
	glEnd();

	glColor3f(1.0f, 0.0f, 0.0f);			//设置当前的绘图颜色为红色
	testThreeView();
	
	glFlush();	//处理所有的OpenGL程序
}

// 初始化OpenGL场景
void Initial() {
	glClearColor(1.0f, 1.0f, 1.0f, 1.0f);		//设置窗口背景颜色为白色
	glMatrixMode(GL_PROJECTION);							//设置投影参数
	gluOrtho2D(-400.0, 400.0, -300, 300.0);	// 投影面上的模型坐标范围
}

int main(int argc, char* argv[]) {
	//testTransTransform();
	//testScaleTransform3D();
	//testSymmetryForXTransform3D();
	//testSymmetryForYTransform3D();
	//testSymmetryForZTransform3D();
	//testSymmetryForXOYTransform3D();
	//testSymmetryForYOZTransform3D();
	//testSymmetryForZOXTransform3D();
	//testMiscutTransform3D();
	//testRotationForXTransform3D();
	//testRotationForYTransform3D();
	//testRotationForZTransform3D();
	//testThreeView();

	glutInit(&argc, argv);						// glut初始化
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);//初始窗口显示模式
	glutInitWindowSize(800, 600);			//设置窗口的尺寸
	glutInitWindowPosition(200, 200);			//设置窗口的位置
	glutCreateWindow("基本图形生成");			//创建一个窗口
	glutDisplayFunc(Display);					//设置当前窗口的显示回调函数
	Initial();										//完成窗口初始化
	glutMainLoop();									//启动主GLUT事件处理循环	
	return 0;
}

其中旋转函数的定义，见专栏中文章（计算机图形学：三维图形的几何变换），其中有关于用到的几何变换函数的详细定义。

---

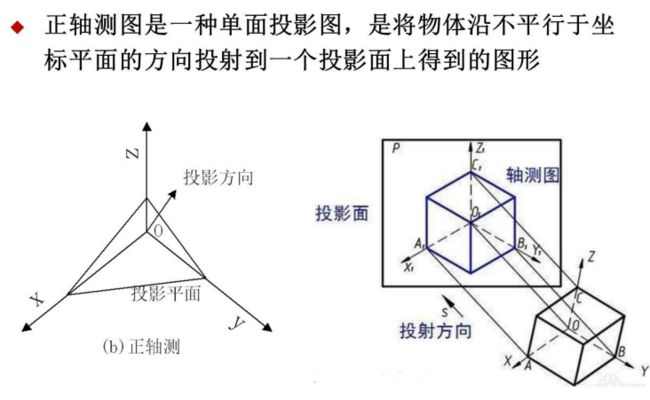
Ⅱ. 正轴测图

三视图与正轴测都属于正投影，但各有优缺点，如下：

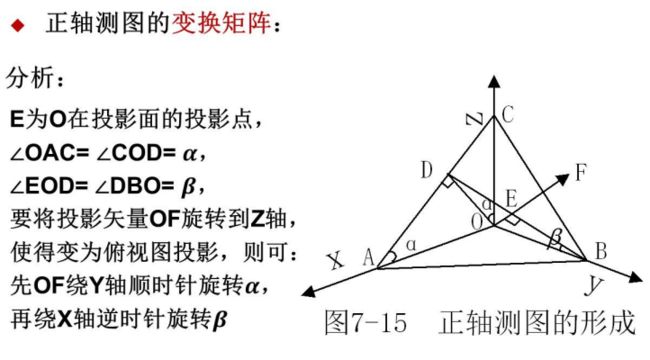
按照投影面与三个坐标轴之间的夹角，可以分为等轴测、正二侧、正三侧。

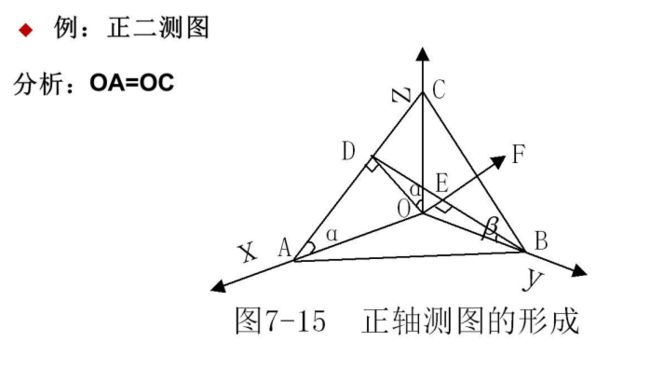
正轴测的变换矩阵与公式推导：

---

2. 斜投影

斜轴测图：将三维物体向一个单一的投影面做平行投影，但投影方向不垂直于投影面所得的平面图形。常用的斜轴侧图有斜等侧图和斜二侧图。

---

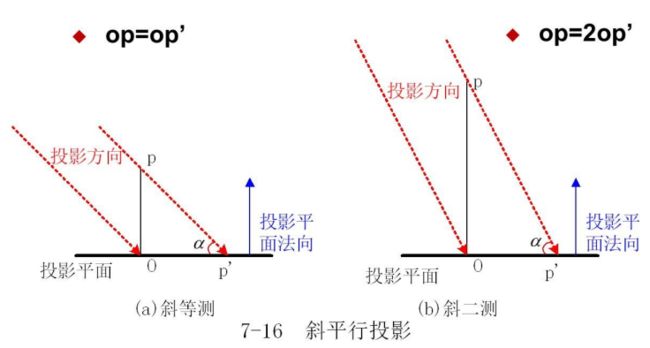
Ⅰ. 斜等测图

后面用到了补充……

---

Ⅱ. 斜二侧图

后面用到了补充……

---

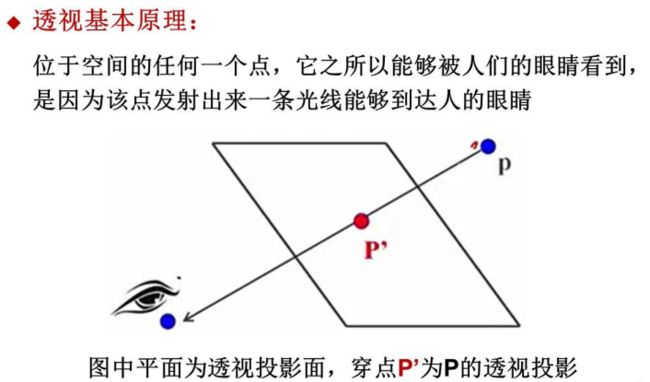
三、透视投影

---

1. 一点透视

两点透视和三点透视较为复杂，在此不再展开介绍。

---

四、三维观察基本流程

这里还有些不懂，懂了的时候再来补充 hahaha~ ヾ(≧▽≦*)o

---

the end……

三维图形的几何变换到这里就要结束啦~~到此既是缘分，欢迎您的点赞、评论、收藏！关注我，不迷路，我们下期再见！！

我是Cherries，一位计算机科班在校大学生，写博客用来记录自己平时的所思所想！
内容繁杂，又才疏学浅，难免存在错误，欢迎各位大佬的批评指正！
我们相互交流，共同进步！

注：本文由非妃是公主发布于https://blog.csdn.net/myf_666，转载请务必标明原文链接：https://blog.csdn.net/myf_666/article/details/129877371