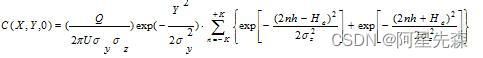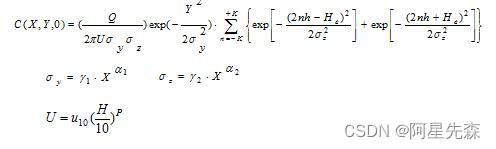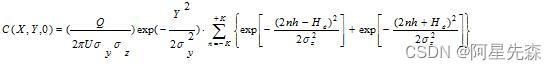vb+access大气污染模型系统
数据模型就是按专业的要求,用数字方式描述自然界的事物或现象以及他们的关系。
我们通过对地区的具体数值和情况的观察,对大气质量状况做出分析,建立一个符合当地情况的大气污染模型,用来测量大气污染浓度,并根据污染浓度评价出当地的空气质量。由于地理信息以及环境的“模糊性”,我们可以简化模式,得出最大值,可以认为是污染源的污染浓度。
在我们的设计中,就是首先要建立一个大气污染的模型,并根据模型云用MATLAB语言算出浓度值推导出当地空气质量,不但如此,还要可以根据别的地区的空气浓度和具体的环境数值反推出符合当地的空气质量系数。
最后,还建立了一个界面和数据库,用来存放模式计算的数值!
世界的本源是模糊的,人类的认知水平也是从混沌空蒙走向明晰和精确,从抽象的语言描述到具体的数字表示。17世纪牛顿和莱布尼兹创立了微积分,更使人类的认知产生了一个飞跃,以致数学被人们看成是“严谨、精确”的化身。但随着人的认知水平和科学技术的发展,人们开始认识到,复杂的事物是难以精确化的,复杂的系统很难用精确的数学进行描述:丰富多彩的世界绝不是Contor的集合所能描述的。例如“胖和瘦”、“快和慢”、“美和丑”等概念是没有明确的界限的。尽管我们对什么是“秃头(bald)”和“正常头发(hirsute)”有一个非常清晰的概念,但用数学上精确语言对二者的定义却会得到相悖的结论。其次数学的应用领域逐渐扩大,各门学科甚至过去与数学很少联系的生物学、心理学等社会和人文学科都迫切要求数字化、定量化地描述和分析。但这些学科的大多数概念是模糊的,很难用精确的数学方法处理其语义属性,需要有研究和处理具有模糊性概念的数学来为这些学科提供新的数学描述语言和工具。于是有人开始研究模糊。
1、1模糊集合论的基本原理
1、1、1模糊的产生
1965年美国学者L. A. Zadeh的“fuzzy sets”的著名论文,宣告了“模糊数学”正式诞生。Zadeh认为,有时精确远不如模糊更符合事物的本原。在现实生活中复杂事物要想绝对精确是不可能的,本来就是含糊的事物要想精确化也是不可能的,实际上只是把不准确程度降低到无关紧要的水平罢了。Zadeh在这篇论文中,首次成功地运用数学方法描述了“模糊性”,突破了Contor集合论的二值逻辑的束缚,解决了J.Tukasiewicz和E.Post等人的三值逻辑论和多值逻辑论的无法处理的一些关键概念,提出了一个求解逻辑问题的更一般的、更抽象的方法。其关键思想是承认由于客观事物的差异所引起的中介过渡的不分明性,承认渐变的隶属关系。一个元素可以部分地属于某个集合,一个命题可以部分地为真。其中隶属函数是描述某个元素摸糊性的关键,是模糊数学赖以建立和发展的莫基石,
自1965年来,模糊数学已渗透到了数学的各个分支,如模糊拓扑、模糊逻辑、模糊概率、模糊规划、模糊系统等方面己取得了重大的理论研究成果,模糊分析理论与方法在气象预报、医疗诊断、人工智能、模式识别和模糊控制、商品评价,以及农林地质等学科方面显示了其强大的生命力。
模糊数学理论的飞速发展和应用的广泛普及,主要在于它反映了人脑的不确定性思维,利用数学的方法妥善处理了生活中“亦此亦彼”的现象。是人类认知水平自然发展的过程,也是人类认知过程的一种转变和飞跃。
事实上,早在1923年,著名哲学家罗素就论述过模糊性在现实生活和自然界各个领域中的客观存在问题。恩格斯曾明确而高度概括地指出“一些差异都在中间阶段融合,一些对立都经过中间环节而相互过渡”;“辩证法不知道什么绝对分明和固定不变的界限,不知道什么无条件的非此即彼,它使固定的形而上学的差异互相过渡,除了‘非此即彼’,又在适当的地方承认‘亦此亦彼’,并且使对立互为中介”。因此,模糊性是客观存在的自然属性的论点有着坚实的哲学基础(陈守煌,1988).模糊性不是由于人的主观认识达不到客观实际而造成的,而是事物的一种客观属性,是事物的差异之间存在着中间过渡,是事物或现象的归属界限的不确定性所带来的亦此亦彼的表征结果。从另一方面讲,模糊性也不是由于人的认知思维的不确定性在造成的,而恰恰相反,是人的思维力求确切反映自然事物或现象的本质属性时的一种客观再现,亦即模糊性是事物的本质属性,“模糊”模式是一种能较好地模拟人类思维模式的工具。
因此,模糊数学并不是“模糊”的数学,它是采用严格的、精确的数学手段处理模糊现象的一门数学。模糊数学是传统数学的延伸和推广,与传统数学一样,有着严格的数学理论基础。从认识发展的观点来看,它实际上也是对客观世界的一种精确反映,体现了人类认识能力的深化,是以模糊达到精确的手段。
1、1、2模糊集合论的基本原理
模糊数学可称为是继经典数学和统计数学之后数学的又一个新发展,它将Contor集合隶属函数的二值值域{0. 1}扩展为模糊集合隶属函数的连续值域{0.1},为描述和反映客观世界中各种模糊事物和现象如模糊概念、模糊目标和约束以及各系统之间的模糊关系提供了有效的手段。模糊数学打破了普通集合论的束缚,并与数学严密整合,其特征在于:
- 2环境系统的模糊性
1、2、1环境质量的好坏和环境质量的价值
环境科学所指的环境是围绕人群的空间以及其中可以直接、间接影响人类生活和发展的各种自然要素和社会要素的总体,所以环境质量的优劣是根据人类的某种要求而定的,是环境的总体或环境中的某些要素对人类的生存和繁衍以及社会经济发展的适宜程度在人的大脑中的反映。
环境质量的好坏、优劣可以用定性和定量的方法描述,用于定量描述的有各种质量参数值、指标和质量指数值等,用于定性描述的是各种反映其程度的形容词、名词等。人作为主体对环境的评价虽然以客观数据为基准,但由于比较的主体认识水平的不同、价值取向不同,以及生存环境和意识形态的不同.对同一个评价对象会因评价主体的不同而得出不同的评价结论。例如,人们对大气污染都有一个统一的认识,空气清新的环境质量好,污染严重的环境质量就坏。但评价空气污染由“优”到“严重污染”及其中间过渡等级的客观数据是渐变的,并没有一个严格的划分。其差异不是绝对的,从差异的一方到另一方没有明确的界限,中间经历一个从量变到质变的连续过渡过程,这是差异的中介过渡性。由差异的过渡性而产生划分上的非确定性就是模糊性。另外,人们对各种传媒工具和家用电器的微波辐射形成的“电子烟雾”的认识还处于朦胧的阶段,对人体健康而言,一个长时间的作用域内的小剂量辐射所表现出瞬时环境状态还无法用定性或定量的数据描述,尽管对某一个具体的环境它是客观存在的。这种概念内涵中的不确定性就是前面所说的一般模糊性。
环境质量的效用程度还表现为环境价值的高低。环境价值常以一个地域、国家和社区中人们公认的社会原则、伦理、习惯、环境标准进行度量,是人们在长期和反复的社会实践中形成的一种特殊的价值观,受制于特定区域内人们的历史文化传统、社会经济发展水平、环境觉悟程度及所处的地理环境。人类还没有对各种各样具体环境要素和因子的价值形成统一认识,绝大部分的认识还属于可表达性认知思维中的一种广义模糊性。
1、2、2环境系统的复杂性意味着模糊性
L.A.Zadeh创立模糊理论时发现一个互不相容原理:“当系统的复杂性增长时,我们对系统的特性作出精确而有意义的描述的能力将相应降低,直至达到这样一个闭值,一旦超过它,精确性和复杂性将变成两个互相排斥的特性”。这就是说,复杂性越高。有意义的精确化能力便越低;而精确化越低,便意味着系统具有的模糊性越强。因此环境系统的复杂性就意味着模糊性。
首先,环境系统是一个复杂的、多层次的巨系统。
环境系统是由自然环境、生态环境和社会环境三个子系统组成。每个子系统又包括众多次级子系统。如从组成要素分,自然环境系统包括大气环境系统、土壤环境系统、水文环境系统、地质环境系统。从环境规划与管理角度分,大气环境系统有可分为大气污染监测系统、大气污染或大气环境质量评价系统、大气环境污染控制系统等更低一级的子系统。形成一个多层次系统。不但具有相互作用、相互联系、互有因果的关系,而且在各系统内部也在不断发生物资、能量和信息的交换,不同层次之间、同层次各子系统之间与外部环境也是开放的。这样就形成了一个多层次、多输入、多输出一种复杂巨系统。对这样一个系统的描述、评价将会因其复杂性而使精确性降低。
其次,环境的决策过程和结果也充满着模糊性。
环境系统的复杂性不仅表现在组成环境的因素众多,还表现在其属性的多样性。有些因素是可以用一般的数学方法量化,为清晰性指标,如污染物浓度对应的环境指标、环境污染等级、治理费用等;但许多用语义值描述的概念则难以完全定量化,为非清晰性指标,如社会效益、生态影响等指标。
在环境系统的决策过程中,所规定的系统目标和约束不是固定不变的,并且允许有一定的变化范围:环境系统的决策与决策者密切相关的,人的主观性具有模糊性,对结果影响很大。不同的研究人员,即使是专家积累在大脑的经验和信息也会因人而异。
总之,模糊事物和现象在环境系统中是客观存在的,这就决定了在环境科学的发展过程中必须重视模糊数学理论与方法的应用。
- 3模糊理论在环境科学和地理信息系统中的研究现状
1、3、1模糊理论在地理信息系统中的研究现状
模糊集理论在地理信息系统中的应用,最早见于有关专题制图中地类要素边界“不精确性”问题的讨论。早在计算机技术大规模用于机助制图和GIS之前,对如何妥善解决地类边界的不精确性问题就成了专题地图中与表示地理数据有关的众多难题之一。专题图上的实体由它们的空间方位和非空间的属性定义.通常一个多边形表示由一个、或一组属性组成的一个相对均质的地理区域,多边形的边界线两侧为不同特征区域。边界的不精确性是指实地情形与图上多边形表述的信息存在不一致性,这包括两个方面,属性的不精确性和定位的不精确性。专题图上的多边形边界线通常被表示为明确的线,用以表示和区分具有不同的特征的区域(Burrough 1986)。这在处理可以明确定义的地籍图、人口统计图和行政区划图的边界问题时,是可行的。而土壤质量、人口密度的属性特征是连续变化的,它们的边界线只是为了有利于分类和制图表示。不加区别的用同一种线划表示不同地类的边界线可能导致对所表述的信息的误解,尤其是在数学严密的计算机处理过程中。
许多学者曾讨论过,既然地理区域并不总是能被精确地区分,传统边界线的制图方法在计算机制图中就有必要作些改变(Coleman 1980. Robinso 1980、Leung 1987.
Burrough 1986. Chrisman 1989. Fisher 1989).于是模糊集合理论与方法在定位、属性描述、误差和插值方面得到了较好的运用。
为了便于研究,Goodchild. Burrough等人将地理要素按数据类型的表述方法不同,把数据模型分为两类,即精确的目标模型(object model)和连续变化的场模型(field model).
模糊理论在地理信息系统中的应用主要有基于模糊场的误差带(Leung 1987;
Goodchild,1986 )、多边形的叠置与模糊聚类分析。模糊误差带是在属性值连续分布的边界线两侧,以模糊隶属度a(0 模糊集理论在多边形叠置分析中,主要用于解决几个图层叠置后会生成许多子多边形合并后的类别归属问题。通常的方法是依据面积、误差和公共边界线的长度,或是三者的组合。现行软件通常是选择具有最长公共边界的多边形作为合并,但这不能保证属性的最相似性,使误差达到最小。Wang (1996)提出了一种应以模糊隶属度的大小予以合并的方法。至于模糊聚类分析在GIS中的应用则更是一种常见的方法. 1、3、2模糊理论在环境科学研究现状及存在的主要问题 模糊分析理论与方法在环境科学研究中的应用多用于环境监测站点的优化、环境质量评价或环境功能的分区研究。应用方法多种多样,如模糊聚类分析,比较典型的就有:基于相似形关系和模糊关系的方法(包括聚合法和分裂法).基于模糊等价关系的传递闭包法和基于模糊图论的最大树法.以及基于目标函数的方法等等,但上述这些方法不适用于大数据量的情况,难以满足实时性高的场合,更重要的是当聚类因子较多时,无法知道聚类结果的综合误差的大小。 其次,模糊数学在环境科学中的应用研究大多数只局限于模糊数学的应用方面,如模糊关系的推导、算法选用、模型设计,更多的是对计算结果的分析。而对模糊数学的一些基本原理和方法在应用中的具体实施研究得不够,尤其是模糊数学怎样与某一学科中的应用更有效的结合起来。例如,与模糊隶属函数息息相关的权重计算就一直是模糊数学应用所研究的重要内容之一。权值的计算方法很多,但是根据权值的可能分配去筛选因子,还是根据分类、评价或决策结果通过迭代反求筛选因子及其权值。并且由于模糊数学本身用于分类和评判的模型不够完善,往往导致实际应用中有些分类结果不准确或分类结果不可信,如入选因子过多,权值分散:所选用的模型是主因子决定型、突出主因子的模型,还是综合评判模型;有些特征对分类是没有影响的,但怎样通过实验或合理的计算(结合具体学科)剔除无关特征等等。这些看似简单,与分类、评判和决策结果有着必然联系的问题却容易遭受忽略,研究的相对较少。 除此之外,模糊集理论一直广泛用于数据库结构和数据库操作,其他领域研究工作包括数据库中的数据的模糊表示(Buckles、Petty 1982)、模糊关系推论语言(Baldwin和Zhou 1984)、非精确条件下GIS的设计(Robinson和Strahler,1984)、土壤测量和评价的模糊数学方法(Burrough 1989).模糊空间关系的机器获取(Robinson 1990)、农业土地适应性分析、评价的模糊方法(Wang 1990、Hall 1992)和模糊补偿能力的土壤信息系统(Kollias和Voliotis 1991)等等. 因此,在此次的设计模式: 中,用的是模糊概念,不可能用很精确的值,我们可以先设Y为0,这样就可以算出在X方向扩散的污染浓度,也既是最大污染浓度。 第二章、MATLAB简介 MATLAB语言起源于1980年美国学Clever Moler教授在线性代数领域的早期工作,于1984年出现了MATLAB的第一个商业版本。MATLAB语言具有强大的数学运算能力、方便实用的绘图功能及语言的高度集成性,使其在许多科学与工程领域的应用越来越广,并且有着更广阔的应用前景和无穷无尽的潜能。 2、1 MATLA语言简介 MATLAB语言是国际上最流行的科学与工程计算的软件工具,和具有广泛前景的全新的计算机编程语言,称为“第四代”计算机语言。MATLAB可以对矩阵领域所有内容进行极为简便的处理,相比于其它高级语言处理此问题时具有无可比拟的优越性。利用MATLAB语言处理数值分析问题变得十分简单和明了。此外,基子此语言开发的许多专用数学工具箱,给处理相关问题带来了方便。总之,在数值计算领域MATLAB语言是很优秀的软件。 MATLAB语言具有强大的数值计算能力,而且还有非常强大的图形功能。可以绘制出具有二维、三维以及四维表现图形,且自身带有各种特殊用途的图形。可以满足许多方面的用途,MATLAB强大的图形功能为科学与工程计算数据分析带来了极大的方便,能够非常直观的进行分析与判断,这些比起Fortran语言和C语言等计算机语言具有很大的优越性。 MATLAB软件带有许多工具箱。每个MATLAB的工具箱实际上是一组实现某种功能的特定MATLAB函数。这些工具箱本身就是用MATLAB语言设计的,同时又大大地扩充了MATLAB本身数值线性代数功能。MATLAB软件所带工具箱有最优化工具箱,偏微分方程工具箱。样条插值工具箱,统计学工具箱。符号运算工具箱等等。本程序中就同时利用了最优化工具箱与样条工具箱解决了某些环节的问题。 2、2 MATLAB语言编程基础 这一部分具体说明MAT1AB语言编程的基础知识,其中包括基本数据类型,基本运算及输入输出,程序流程语句,数据结构等。 2、2、1函数调用语句 函数调用语句的基本结构为: [返回变量列表]=function(输入变量列表) 其中函数名的要求和变量名的要求是一致的,一般函数名应该对应在MATLAB路径下的一个文件,即m文件。在大规模程序议计中函数调用语句是最常用的,各个函数调用语句就构成了程序的框架。大气污染模型程序中就构造了二个函数。这些函数通过一定的逻辑关系相互调用,完成了程序的全部功能。 在MATLAB语言中还为特定常数保留了一些名称。如下所列: eps——机器的浮点运算误差限。 Inf——无穷大量+∞的MATLAB表示。 NaN——不定式,通常由0/0运算、Inf/Inf及其它可能的运算得出。NaN是一个很奇特的量。在三维图形处理中利用它可以作图形的剪切处理。 pi—圆周率x的双精度浮点表示。 2、2、2矩阵的MATLAB表示 前面讲到MATLAB语言最基本的出发点是一个“短阵实验室”,即它是以矩阵为基本变量单元的。 在MATLAB语言中表示一个矩阵的方法很简单。例如,矩阵可以由下面MATLAB 的语句直接输入到工作间中。 A=[ a11 a12 a13;a21 a22 a23;a31 a32 a33] 矩阵的内容有方括号括起来的部分表示,而在方括号中分号表示矩阵的换行,逗号或空格表示同一行矩阵元素之间的分隔。以下对子矩阵的表示均采用这种方法, MATLAB语言定义了独特的冒号表达式来给行向量赋值,其基本使用格式为: A=s1:s2:s3; 其中,s1为起始值,s2为步距,S3为终止值。如果s2的值为负值,则要求s1的值大于s3的值,否则结果为一个空向量(用[]表示)。如果省略了的值,则步距取默认值1, 这里介绍几种MATLAB语言中矩阵最基本的变换与计算,它们是用MATLAB语言编程都不可缺少的内容,以上面的3x3矩阵为例进行说明和演示。 (一)矩阵常用空量 1、矩阵增加行数 如B=[A:[A41 A42 A43]]表示了一个矩阵,其MATLAB表示为: B=[a11 a12 a13;a21 a22 a23;a31 a32 a33;a41 a42 a43] 即在原来矩阵的下面附加上一个行向量。在运用此方法时注意保证各行的元素个数要相同,否则给出错误信息。 2、矩阵增加列数 如"B=[A,[a14;a24;a34]]表示了一个矩阵。其MATLAB表示为: B=[a11 a12 a13 a14;a21 a22 a23 a24;a31 a32 a33 a34] 即在原来A矩阵的右面附加上一个列向量。在运用此方法时注意保证列的元素个数要相同,否则给出错误信息。请注意1和2矩阵在表示方法上的不同。 3、A (i,j)表示矩阵第i行第j列的元素,如A(2.3)=a23。 4、矩阵提取子矩阵 如B=A([i,j],[m,n])表示从矩阵A抽取第i行第m列第j行第m 列的元素以及第i行第n列第j行第n列组成的子矩阵。矩阵的维数是3x2。逗号前的方阵表示行的位置,逗号后的方阵表示列的位置。其MATLAB表示为:B=[aim ajm akm;ain ajn akn]。 5、冒号表达方式 在提取子矩阵式时,如果行〔或列〕的位置用冒号代替。则表示取所有行(或列)。 如B=(A:,[m,n])表示B=[a1m a2m a3m;a1n a2n a3n]。 C=A([i,j],:)表示C=[ai1 aj1;ai2 aj2;ai3 aj3]。 A(:)也是一种冒号表达方式,其意义是将所有元素按列构成一个列向量。A(:)=[a11;a12;a13;a21;a22;a23;a31;a32;a33] 6、矩阵的维数确定 矩阵的维数确定是通过MATLAB语言所带的size()函数实现的。括号内是某一矩阵例如A。得到的值是一个1x2矩阵。表示矩阵A的维数。第一个元素是矩阵的行数。第二个元素是矩阵的列数。 例: 对于上面矩阵 A和A(:),size(A)=[3,3],size(A(:))=[9,1]等。 对于行或(列)向量,即矩阵的特例,也可用length()函数求得元素的个数。例如, length(A(:))=9。 7、矩阵的变维操作 矩阵的变维操作是通过MATLAB语言所带的reshape()函数实现的。用法如下: reshape(原矩阵,新矩阵的行数,新矩阵的列数)。 例如,D=[d1 d2 d3 d4 d5 d6 d7 d8]则 reshape(D,4,2)=[d1 d2 d3 d4;d5 d6 d7 d8] 如果使用的新维数下的矩阵总元素不等于原来矩阵的元素数,则将给出错误的信息。 8、end算符 end算符很常用,它表示某一维的末尾下标。例如, A(2:end,[1,3])=[a12,a13;a32,a33] (二)矩阵代数运算 1、矩阵转置 MATLAB下的矩阵转置用矩阵左上角加撇号实现运算的。例如,矩阵A的转里为A'。例如A=[a11,a12,a13;a21,a22,a23;a31,a32,a33] .则A’=[a11,a21,a31;a12,a22,a32;a31,a32,a33]。 2、矩阵的加减法运算 从线性代数理论中已经了解到只有相同维数的矩阵才能够进行加减运算,运算的方祛是对应元素进行加减。在MATLAB中也是这样的,很简单。在编程中用加号与减号书写即可。 3、矩阵的乘法 在MATLAB中矩阵的乘法与线性代数理论中的规定是相同的。在实际编程中在符合要求的两个矩阵之间用乘号“.‘’连接即可实现。这种乘法要与后面提到的点乘运算相区别。 4、矩阵的除法 在MATLAB中矩阵的除法要涉及到线性代数理论中的矩阵求逆运算,并且定义了两种除法运算:左除“\”和右除“/”。A\B表示由Gauss消取法来获得线性方程AX=B的解x即X=AB。 B/A相当于求方程XA=B的解。A为非奇异时B/A为BA-1。左除与右除由下面的关系。B/A=(A'\B')’。 5、矩阵的翻转 MATLAB提供了一些矩阵翻转处理的命令,有fliplr(),flipud()等。分别表示将矩阵左右翻转、上下翻转的操作。例如,对于矩阵A, fliplr(A)=[a13,a32,a11;a23,a22,a21;a31,a32,a33] flipud(A)=[a31,a32,a33;a21,a22,a23;a11,a12,a13] 6、矩阵的乘方运算 这是乘法运算的扩充,如果给定一个矩阵A求其n次方(n为任意常数)表示为A‘n。 7、 点运算 MATLAB中定义了一种特殊的矩阵运算,即点运算。矩阵之间的点运算是它们对应元素的直接运算。这就与矩阵的加减运算的方法一样了,也要求矩阵的维数要相同。点运算的表示方法如下, A.B表示A、B之间对应元素相乘。A/ B表示A、B对应元素相除。A.^B表示A的每一个元素的n次方等。点运算在编程中很有用。它使所有数据周时进行一种运算,简化了程序的编写。而用其它程序编写需进行一次循环才可完成计算。 (三)矩阵逻辑运算 在进打矩阵的逻辑运算时矩阵的维数应相等或其中之一是标量。否则不能计算,计算时为对应的元素进行计算。 1,矩阵的与运算 在MATLAB下用&号表示矩阵的与运算。其定义为,如果两个数均非0,则该结果元素的位为1,否则该元素为0。 2、矩阵的或运算 在MATLAB下用|号表示矩阵的或运算。其定义为:如果两个数均为0则该结果元素的值为0。否则该元素为1。 3、矩阵的非运算 在MATLAB下用~号表示矩阵的非运算。其定义为,如果两个数均为0则该结果元素的值为1。否则该元素为0。 (四)矩阵的比较关系 MATLAB中定义了各种比教关系,如“>”(大于关系),“<”,(小于关系),“==”(等于关系)“>=”〔大于等于关系〕,“<=”(小于等于关系)。这些关系 运算都是针对两个矩阵对应元素的。故要求运算时矩阵组数要一致或其中之一为标量。在进行计算时,对应元素进行比较,若关系满足,则将结果矩阵中该位置的结果置为1,不满足则置为0。 (五)几个常用的工具矩阵 以下几种常用的工具阵,除单位矩阵外,其它的几乎没有任何具体意义,但在是其中有十分广泛的应用。如定义矩阵的维数、赋迭代的初值等。这类工具阵主要包括:全零阵、单位阵、全一阵和随机阵。 1、全零阵 全零阵由函数zero()生成,其主要调用格式为: zeros(N)——生成NXN的全零阵。 zeros(M,N)——生成MXN的全零阵。 zeros(size(A))——生成与A相同大小的全零阵。 2单位阵 单位阵可由函数好eye()生成,其主要调用格式为: eye(N)——生成NXN的单位阵。 eye(M,N)——生成MXN的单位阵。 eye(size(A))——生成与A相同大小的单位阵。 3、全一阵 全一阵由函数ones()生成,其主要调用格式为: ones(N)——生成NXN的全一阵。 ones(M,N)——生成从MxN的一阵。 ones(size(A))——生成与A相同大小的全一阵, 4、随机阵 rand(N)——产生一NXN均匀分布的随机矩阵。元素的值在(0.0,1.0)区间内。rand(M,N)——生成MXN的随机矩阵。rand(size(A)——生成与A相同大小的随机阵。 2、2、3 MATLAB语言的程序流程语句 作为一种程序设计语言,MATLAB提供了循环语句结构、条件语句结构、开关语句结构及新的试探语句。 〔一〕循环语句结构 循环语句有两种结构:for…end结构和while …end结构。它们不完全相间。各有特色。具体的结构可见[1,4] (二)条件转移结构 MATLAB语言还提供了各种条件转移语句的结构,使得MATLAB语言更易使用。 MATLAB提供的条件语句最简单的格式是由关键词if引导,此外,MATLAB还提洪了其它两种条件结构,if…else格式和if…elseif…else格式,其格式见 [17,20]: (三)开关结构 MATLAB从5.0版开始提供了开关语句结构,基本语句结构见[17,20], (四〕试探语句结构 MATLAD提供了一种新的试探性结构,其一般形式见[17,20]。 2、2、4 MATLAB中新的数据结构 在MATLAB中有许多新的数据结构如数据结构体、类与对象、单元结构。在大气污染模型程序中。有些数据结构没有涉及到,现仅就单元(cell)结构进行说明。因为在程序设计过程中单元结构应用得很广泛。 单元给构是把不同的数据都归纳到一个变量中,而这个变量称为单元。单元结构的表示方法类似于带有下标的矩阵和多维数组,但这些下标不是用圆括号括起来,而是用大括号扩起来,与矩阵的记法不一样。在矩阵和多维数组中。每个矩阵元素都应该有相同的属性,而单元结构则没有此要求,用户可以把各种不同属性的数据全部归并到一个单元变量中,因而它的应用更具有灵活性。例如,有时不同维数的矩阵需要同时进行一种操作,用单元结构就能够实现所有数据的输入,否则就需要对每一个矩阵单独进行输入。这对于大规模的数据输入是不可能实现的。 与矩阵一样,单元结构也可以使用size()和length()来显示其大小。也可以由带有大括号下标的形式访问该单元数据,得出该矩阵的具体内容。例如。对于一个1XN的单元结构B访问第n(n<=N)个单元元素时,则可以输入B{n}即可。如果需要消除单元变量中第m(m<=N)个单元元素,则可以用命令B(n)=[]。 2、3 MATLAB语言与科学计算 前面提到MATLAB的最大优势是矩阵运算,因此矩阵的各种运算以及线性代数的运算用MATLAB进行解决都变得非常容易。MATLAB语言所带的大量的内在函数也为诸如微分方程的数值解,积分运算带来了便利的求解过程。由MATLAB语言编写的一些数学计算工具箱使得许多数学分支学科的计算和研究变得简单易用。其中许多内容在大气污染模型程序中都有反映,使得程序的设计更加简洁和紧凑。 2、3、1矩阵的非线性运算 矩阵的线性运算前面已经说明,现在说明如何对矩阵进行非线性运算。事实上,MATLAB提供了两类函数。其中一类是对矩阵的各个元素进行单独运算的,第二类是对整个矩阵进行运算的。由于第二类在实际工程中应用较少,故重点放在第一类。第一类有一些函数运算,主要如下: abs()—求绝对值(模)运算; aqrt()—求平方根函数; exp()—指数函数; sin(),cos()—正弦,余弦函数: asin(),acos()—反正弦、余弦函数; round(),floor(),ceil(),fix()—取整数函数,筹等。 标准调用格式为: B=函数名(B), 例如B=sin(A) 前面余弦曲线及三维曲面图的例子已经给出这一类计算的模式。可参阅。这里对四个取整函数具体说明如下:round()表示对矩阵的所有元素取四舍五入:floor()表示对矩阵所有元素朝-∞方向取整数,ceil()是朝+∞方向取整数;fix()表示对矩阵所有元素朝0方向取整数。 据插值运算在工程实际上运用很广泛。大气污染中也不例外地应用了。在地貌较为复杂的情况下。如果对起伏状况进行很好的描述就需要有各个点的高程数据。但是很多情况下由于地块范围较大,坐标点的数量非常大,输入高点的数据量是庞大的,对全部数据进行输入是不现实的,甚至是不可能的。这时需要用较少的点的数据来确定出所有点的数据,就成为插值问题。当选择了一些有代表性的点后,利用MATLAB数据插问题可以方便地得到插值结果。需要强调一点,已知点的选择对于插值结果的好坏有很大关系,因此在选择点的时候需要对问题的具体状况先做细致的分析。例如对于相对平缓地带点可以选得疏松一些,起伏变化大的地带点就应当选择的密-些。 (一)一维数据插值 一维插值问题可以由interp1)函数解决,该函数的调用格式为: y1=interp1(x,y,x1,方法) 其中x和y两个向量分别表示给定的一组自变量和函数值数据,x1为一组新的插值点而得出的yl是在这一组插值点处的插值结果。插值方法一般可以选择’linear(线性的,次此项是默认的),还有‘cubic ’(三次的)和‘spline’〔样条型〕等。 函数polyfit()可以对给定己知点数据进行多项式拟合,调用格式为: p=polyfit(x,y,n) 其中,x和y两个向量分别表示给定的一组自变量和函数值的数据,n为预期的多项式阶次,返回的P为插值多项式系数。 (二)二维数据插值 MATLAB下提供了二维插值的函数,如interp2(),该函数的调用格式为: Z1=interp2(x0,y0,z0,x1,y1,‘方法’) 其中x0,y0,z0为已知的数据,而x1,y1为插值点构成的新的网格参数,返回的z1矩阵为在插值网格点处的函数近似值。用前面给出的一个曲面生成函数 命令生成网格图。如图2-8(a)。 [x1,y1]=meshgrid(-3:6:3,-2:4:2); z=(x^2-2*x)*exp(-x^2-y^2-x*y); subplot(121); mesh(x,y,z). 选较密的插值点,则可以用下面的MATLAB语句采用默认的插值方法进行插值,得出的图如图2-8(b)所示。 [x1,y1]=meshgrid(-3:2:3,-2:2:2); z1=interp2(x,y,z,x1,y1); subplo1(122); mesh(x1,y1,z1) 从图中看到,默认的插值方法生成的三维表面图还显粗糙。如果选用立方插值选项或样条插值就比较理想,插值结果如图2-9(a)和2-9(b)。基于这种情况,在网程序中对地块数据进行插值运算时选用的插值方法为样条插值。 Z1=interp2(x,y,z,x1,y1,‘cubic’); Z2=interp2(x,y,z,x1,y1,‘spline’); Subplot(121),mesh(x1,y1,z1); Subplot(122),mesh(x1,y1,z2); 第三章、大气污染模型的创建和简化 3、1 地理信息系统中建立模型 现实世界中的某些事物可以称作为现实原型。模型就是对这种现实原型的一 种抽象或模拟,而且这种抽象或模拟并不是简单的“复制”,而是强调原型的本 质,扬弃原型中的次要因素。因此,模型既反映原型,又不等于原型,或者说它 是原型的一种近似,用一定的表现规则描写出来的简明映像。 在地理学研究中便用的模型,称之为地学模型。因其具有空间特性,也称为 空间型。地学模型用来描述地理系统各个要素之间相互关系和客观规律,可以使用信息的、语言的、数学的或其它表达形式,反映地学过程及其发展趋势或结 果。 模型通常是用来解决地学问题的有效手段,通过在地理信息系统中引入地学 模型,可以使得地理信息系统具有解决一定空间问题的能力。这种发展使得地理 信息系统的功能与技术都发生了重大变化,导致地理信息系统的多学科融合。 从地理信息系统的发展及其特点,我们可以看出,模型是地理信息系统应用 的核心。地理信息系统主要依赖于应用模型,特别是模型的分析能力与模型的模 拟能力,并生成相应的解决方案供用户选择,以实现相应的决策。 3、1、1 地学模型的特点 由于地学模型所处理对象的特殊性,与普通的数学模型相比,地学模型具有 以下的几个特点: 空间性:地学模型与地理对象的空间位置、分布以及差异密切相关,在应用中必须注重地学模型的空间运算特征。 多样性:地学模型的表示形式,可以是数学的,也可以是非数学的,并且地学棋型在人脑中的表示与在计算机中的表现是不同的。模型一般都是具有语义背景的,在人脑中,模型通常表现为某些规则、语义或者是公式,但在计算机中,模型表现为程序代码的形式,并且地学模型一定可以用程序的形式进行表示。在应用中,就需要将模型的不同表达形式进行转换,最终通过计算机进行计算分析。 复杂性:地理问题通常是比较复杂的,并且受人的干预与影响因素很多。因此,很难用纯数学的方法对地理信息系统中处理的问题进行全面、准确、定量地描述。在地学模型中,模型的描述通常采用定量与定性相结合的方法:模型的设计也必须要考虑到人的因素,留有人为干预的余地。 动态性:任何地理现象都不是孤立的、静止的,时间特性同样也是地学模型 所要考虑的因索。因此,模型的设计需要考虑到时间对模型目标的影响、数据的 更新等问题。 协同性:从认知心理学的角度看,对于相同的地理问题,不同的人由于其背景、知识与方法的不同,会有不同的理解,也即是具有不同的知识。在建模时,地学模型也就具有不同的表达形式与运算结果,但这些并不妨碍模型的应用。关键在于寻找适当的手段,集中群体的智慧优化模型,使之更接近问题的表述与结果的求解,从而使模型更合理、更符合多数人的思维。 由以上特点可见,地学模型建立的过程将非常复杂,特别是涉及到人的认知 过程的不确定性。随着人们对问题理解的深入,地学模型也将是不断变化。 3、1、2 地理信息系统中模型的表达方式 地理信息系统中的模型在计算机中的表达方式,可以有以下几种方式: 第一种方式是数据方式,这种方式本质上是一种关系运算。模型在此种方式 下为一组参数集与表示模型结构特征的数据集合的框架。输入的数据集在此关系 框架下进行关系运算,并输出运算的数据集。也即输入数据集通过摸型参数集合 映射到输出数据集。 第二种方式为逻辑方式。这是一种通过人工智能,使用谓词逻辑、语义网络、逻辑树和关系框架等表达模型的一种方式。比铰常用的谓词逻辑方法,将模型分 解为四个基本组成要素:模型结构、约束集、参数集和变量集。这当中的每一部分都可以使用相关的谓词表示,将数值计算隐含在谓词当中。定量的计算摸型通过逻辑形式表达后,可以与定性的知识统一起来,使用谓词演算的方法,实现对问题的求解。这种方式对于半结构化、非结构化的地学模型表现比较有效。 第三种方式为应用程序方式。将模型的输入、输出以及模型算法通过程序来 实现,通常一个模型是以子程序存贮,每个子程序往往带有通用的程序结构。模 型作为应用程序,嵌入到系统中。这种表达形式的模型,主要适合用于描述结构 化的计算模型,但模型的共享性与灵活性很差。 这三种模型表达方式,分别对应于三种层次的语言:语义逻辑、数学逻辑语言与计算机语言。诚然,这三种语言的差异,将造成不同的信息损失与误差。语义逻辑是对问题描述最有效的方式,这也是地学摸型研究中的一个热点。但模型的最后实现需要由计算机进行,所以,研究这三种语言以及它们之间的相互转换,也是地学模型应用是否有效的一个重要环节。 3、1、3 地理信息系统中模型的存贮 以往在地理信息系统建设中,人们将精力过多地集中于GIS系统的研制,对 于模型本身的投入与系统的应用不成比例。此外,由于很多部是采用应用程序的 方式表达模型,使得模型的共享性与灵活性很差,模型重复建设,使用效率不高。随着地理信息系统应用面的拓展,模型的需求也越来越广,不可避免地需要寻找 新的解决方法。模型库就是为了有效地生成、管理和使用模型而提出来的解决方 法。模型库将是解决地学模型高效利用的一条必由之路,尽管模型库的发展还处 于探索阶段。 目前,模型库系统从功能和功能结构上可以看作由三部分组成,基础模型库、 应用模型库与模型库管理系统。(如图3. l) 基础模型库用来存储通用的、需要多次重复使用的基础模型,其作用类似于 程序设计中的函数库或控件:应用模型库存储用户自己开发用来解决领域问题的模型,相当于程序设计中用户自己开发的程序。通过基础模型库以及建摸工具,可以构造应用模型库;模型库管理系统用来管理、维护基础模型库与应用模型库的应用环境,用户通过人机交互界面与模型库管理系统发生关系,并对模型库进行管理。 模型库借鉴了程序设计与数据库的思想。通过库方式管理系统或用户的模型。用户的模型则可以通过某个特定的模型构造环境,以‘组件式’的方式进行构建,实现模型的重用以及应用模型的构建。模型的表示形式比较统一,模型易于扩充;模型的表示与模型的计算可以独立进行,易于模型的优化、推理;模型表示与计算数据也相对独立,便于模型移植、集成、共享等;这样,可以满足不同用户的需要,而且模型的构建也更灵活、有效、实用。 3、1、4 地学建模方法概述 由前面的讨论可知,模型的表达方式是多种多样的,可以为数学公式、系统 的仿真、图表文字。也可以是专用的形式化语言。在建立模型时,通常采用两种 思路。自顶向下、逐步求精法或自底向上、综合集成法。模型的目标、知识与数 据构成了建模过程的输入。模型的目标指模型研究的目的;知识指现实系统的知识和模型构造的知识;数据指系统的原始信息。通过这三个要素,运用具体的模型构造方法创建系统摸型。当目标与数据一定时,知识就成为建模过程中影响模型有效性的关键。 模型构造方法可以分为;面向过程的建模、面向数据的建模、面向信息的建模、面向决策的建模和面向对象的建模。 面向过程的建模方法是把过程看作模型的基本部分,数据是随着过程而产生 的。 面向数据的建模方法把模型的输入输出看成是最为重要的,数据是模型的核 心。因此,首先定义的是数据结构,而过程模块是从数掘结构中导出的,即功能 跟随数据。 面向信息的建模方法与面向数据建模方法的区别其实就是信息与数据的区别。信息和数据都是信息系统中最基本的术语。数据是指记载下来的事实,是客 观实体属性的值,而信息是构成一定含义的一组数据。面向信息建模方法是从逻 辑数据模型开始的,通过一个全局信息需求视图来说明系统中所有基本数据实体 及其相互之间的关系。然后,在此基础上逐步构造整个摸型。信息模型记录系统 运作所需的信息实体,如大坝、闸、堤坝等,为分析现行系统提供信息的图形化 表示。数据建模的目的是设计和实现满足系统信息需求的数据库结构,即数据建 模支持系统设计。 面向决策的建模方法反映的是决策模型制订原则和机理。通过决策模型的建 立,决策者可以对决策的依据及决策的问题有一个细致的了解,并且有助于发现 新的问题,并据此做出相应的调整。 面向对象的分析方法是利用面向对象的信息建模概念,如实体、关系、属性 等,同时运用封装、继承、多态等机制来构造模拟现实的方法。而面向对象的方 法是采用构造模型的观点,在系统的开发过程中,各个步骤的共同的目标是建造 一个问题域的模型。在面向对象的建模方法中,初始元素是对象,然后将具有共 同特征的对象归纳成类,组织类之间的等级关系,构造类库,也即模型库。应用 时,在模型库中选择相应的模型。 模型可以看作为一种经过提炼后的知识。以上几种建模方法,从不同的角度 对模型进行建模,其在系统中有着不同的应用。如面向决策的建模方法可以很好 地说明决策问题:面向对象的建模方法对于决策系统模型库的建立比较有效;面向信息的建模方法可以有效地利用系统的数据等等。另外,这几种建模方法对模型的分解及组织比较有效,但对于问题的说明有所不足。 此外,以上几种建模方法,都是侧重摸型的分析与摸型的建立过程,对于模 型系统运行时与人的交互性往往局限于某些参数的修改,不能够实现建模过程的 交互,模型一旦建立,如果原始模型所刻画的系统发生变化,模型的计算结果将 会产生很大偏差;在地学中,地学模型侧重于数据或结果的可视化表达,不注重对系统中模型自身的表达,更不要说模型的图形化的分析与模拟的研究;模型的建立往往也是某个领域专家的工作,模型的表达形式对于普通用户根本无法理解;用户若想修改模型以实现自己计算中的某些功能根本不可能,模型的扩展性差:随着网络的发展,模型的建立也往往要求具有协作性,但却缺乏强有力的模型协作与表达工具。 通过这几种建模方法的优缺点分析,将建模方法由物理、逻辑层次提升到概 念层次,从概念上对问题进行分析、理解,并通过可视化技术表达地学模型变得 十分必要。通过概念,不但可以很好地说明模型中各组成部分之侧的关系,也可 以对模型向题进行有效的定义、分解.由于是从概念上进行定义的,接近于人的思维方式与自然语言,可视化方式表达模型易于为人所理解,因此可以降低地学模型应用的门槛。 另外,地学模型可以与地理信息系统相结合,帮助决策者分析问题、辅助决 策,但目前的研究大部分侧重于地理信息系统与地学摸型本身的研究,鲜有从系 统使用者的角度出发探讨问题.造成方法及技术与现实相分离;并且地学模型是事先定义好的特定领域知识与关系知识的体系结构,所做的不过是在实际应用过程中,提供给用户一系列的工具,使用户通过模型运算获得不同计算结果并选择某个运算结果加以应用;对于解决领域问题,使用的模型反映的是模型的构建者对问题的理解与定义,用户无法将自己的隐性知识加以应用,从来也就无法真正有效地解决不断变化的地学问题;只注重问题的结果,对问题处理的过程几乎无效。所以,随着地理信息系统应用的深入,地理信息系统从空间数据管理和显示制图走向模型分析.在确定性模型和统计模型不能满足解决实际问题需要的时候,要求采用新的建模方法,使系统具有面向问题求解的能力因此在开发地理信息系统时,必须开发具有一定智能化水平的模型构建工具和模型管理系统。 3、2 大气扩散模式 3、2、1有风时(u10≥1.5m/s),气态污染物点源扩散模式 以排气筒地面位置为原点,下风向为X轴,下风方地面任一点(X,Y)的一次浓度C(X,Y) (mg/m3): 式中:Q——单位时间污染物排放量,mg/s; X——距排气筒下风向水平距离,m; Y——该点与通过排气筒的平均风向轴线在水平面上的垂直距离,m; σy——垂直于平均风向的水平扩散系数,m; σz——铅直扩散系数,m; α1——横向扩散参数回归指数; α2——铅直扩散参数回归指数; γ1——横向扩散参数回归系数; γ2——铅直扩散参数回归系数; U——排气筒出口处的平均风速,m/s; He——排气筒有效高度,m; u10——10米高度处风速,m/s; He按下式计算: He=H+ΔH H——排气筒距地面几何高度,m; ΔH——烟气抬升高度,m。 在求得C(X,Y,0)之前,我们应输入我们要输入的参数,在输入了参数后,我们可以用字母代入方程中,这样我们就可以随意的改动参数值来算浓度C的大小。在方程如此多的未知数和这么复杂的情况下,我们可以先分块解决,首先,我们先算出 3、2、4小风(1.5m/s>U10≥0.5m/s)、静风(U10<0.5m/s)扩散模式 以排气筒地面为原点,平均风向为X轴,地面任一点(X,Y)小于24小时取样时间内的浓度C(X,Y)的计算公式如下: 3、2、5逆温层破坏时的熏烟模式 熏烟扩散模式,是考虑日出以后,贴地逆温从下而上消失,当逆温层消退形成混合层(混合层厚度为hf),当逆温层消退到烟气抬升高度以上。该逆温层阻止污染物向上扩散,使得污染物在近地面混合,导致地面污染物浓度很高。熏烟模式的地面浓度Cf公式如下: 根据环评技术导则的技术要求,采用较近的一年气象资料,用上式计算敏感目标逐日日均浓度,取某典型日的值作为敏感目标的日均浓度(一年中日均值小于该值的概率为95%)。 此模式也根据上面的模式计算! 模式①适用于计算有风情况下(距地面10米高度处风速u10≥1.5m/s),由排气筒排放(有组织排放)的废气污染物的一次扩散浓度。 模式②适用于计算有风情况下(u10≥1.5m/s),由排气筒排放(有组织排放)的废气污染物的一次扩散浓度在地面上的最大值,及地面最大浓度所对应的与排气筒的距离。 模式③适用于计算有风情况下(u10≥1.5m/s),不经由排气筒排放(无组织排放)的废气污染物的一次扩散浓度。 模式④适用于计算小风(1.5m/s>u10≥0.5m/s)或静风(u10<0.5m/s)情况下,由排气筒排放(有组织排放)的废气污染物的一次扩散浓度。 模式⑤适用于计算逆温层破坏时(逆温层消退到烟气抬升高度以上),由排气筒排放(有组织排放)的废气污染物的一次扩散浓度。 模式⑥适用于计算污染物对敏感目标的日均地面浓度的贡献值。 模式⑦用于计算污染物的卫生防护距离。 模式①:地区(如镇江或丹阳等),风向,季节,稳定度,风速,污染物源强(kg/h或mg/s),排气筒高度,排气筒出口内径,排气速率(m3/h或m3/s),烟气出口温度,地表状况(乡村及城市远郊区或城市及近郊区),预测区域边界距离(米),预测区域内各格点间距离(米),取样时间(一般为1小时),评价等级(分一、二、三级)。 模式②:可并入模式①的计算程序中直接得出。 模式③:地区(如镇江或丹阳等),风向,季节,稳定度,风速,污染物源强(kg/h或mg/s),面源平均排放高度,面源边长(通过计算等效半径得出,等效半径=(S/π)0.5,S为面源面积),地表状况(乡村及城市远郊区或城市及近郊区),预测区域边界距离(米),预测区域内各格点间距离(米),取样时间(一般为1小时),评价等级(分一、二、三级)。 模式④:地区(如镇江或丹阳等),地表状况(乡村及城市远郊区或城市及近郊区),污染物源强(kg/h或mg/s),烟气出口温度,排气筒高度,排气筒出口内径,排气速率(m3/h或m3/s),预测区域边界距离(米),预测区域内各格点间距离(米),稳定度,风速(u10<1.5m/s)。 模式⑤:污染物源强(kg/h或mg/s),烟气出口温度,排气筒高度,排气筒出口内径,排气速率(m3/h或m3/s)。 模式⑥:地区(如镇江或丹阳等),地表状况(乡村及城市远郊区或城市及近郊区),污染物源强(kg/h或mg/s),烟气出口温度,排气筒高度,排气筒出口内径,排气速率(m3/h或m3/s),预测点坐标(预测点距排气筒的座标X=?,Y=?)。 模式⑦:环境标准值,污染物源强(kg/h),面源面积,所在地平均风速(分为三个范围:<2m/s,2~4m/s,>4m/s=,计算系数A、B、C、D(查GB/T13201-91表5,程序中可嵌入该表)。 第四章、系统的设计和实现 4、1 系统简述 在设计大气扩散模型时,我们首先要了解地理信息,要了解在地理环境质量的定性和定量的方法都是模糊的,不可以用具体死板的数值来计算所有的地区的大气状况。由于要用到计算公式像: 如此复杂。所以光是用C语言是很难也很复杂才能完成的,就必须要用到专门处理数学公式的MATLAB软件才可以方便的完成。第一种是把MATLAB里面的一部分.h文件或.lib文件复制到C语言中,然后在对C语言进行仿真,然后用C语言完成程序;或是直接在MATLAB里面用MATLAB语言进行设计。 4、2 MATLAB函数在方程中的的用法 4、2、1 MATLAB的具体函数 首先,我们要用到输入指令,这样就可以随意的输入数值。输入指令为:Q=input('Enter Q>');这种格式,在开始时,我们要把要输入的数全部通过这种格式输入进去。 接下来是乘法、除法和幂的操作,这些操作和C语言的写法一样,乘法用*号除法就用/,在方程没有用到矩阵的情况下不用考虑左除和右除,而在MATLAB里面幂的操作是用^号来计算的! 求根号的操作指令为sort()函数,在模式四里面的形式如下: a2=sort(2*pi); 指数操作在MATLAB里面是很简单的,因为在MATLAB里有现成的exp函数,只要直接在exp()函数的括号里面输入要算的东西,就可以直接算出结果,比如说: 在算求和操作时,也有现成的函数symsum(),形式如下: symsum(函数名); symsum(函数名,变量名); symsum(函数名,变量名,下限,上限); 不过在这之前还必须定义。比如在第一个模式里我用syms Q U Y K He qy qz h n r1 r2 a1 a2 X ,因为在前面定义的时候必须要把在求和里面用到的所有未知数和参数只有这样,才能在下面的sumsum()里识别。 未完待续。。。。 ![]() 作为例子说明如何使用二维插值函数。假设仅知道其中较少的数据,按前面生成曲面网格图的
作为例子说明如何使用二维插值函数。假设仅知道其中较少的数据,按前面生成曲面网格图的![]() 设它等于sum1,接着计算出
设它等于sum1,接着计算出 、
、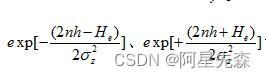 设它们分别等于sum2、sum3、sum4。这样就使的很复杂的式子简单化,不但看起来直观,而且错误也可以很方便的看出!由于要用到求和公式,我们就先保留sum3和sum4里的n,然后我们把sum3和 sum4相加,令它为sum5,这样就可以直接对sum5里的n求从-K到K的和,这样就可以算出浓度C的值了。不过方程里面的σy 、σz 和U都不是直接给出的,可以用
设它们分别等于sum2、sum3、sum4。这样就使的很复杂的式子简单化,不但看起来直观,而且错误也可以很方便的看出!由于要用到求和公式,我们就先保留sum3和sum4里的n,然后我们把sum3和 sum4相加,令它为sum5,这样就可以直接对sum5里的n求从-K到K的和,这样就可以算出浓度C的值了。不过方程里面的σy 、σz 和U都不是直接给出的,可以用  求得。
求得。
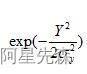 ,这样就可以直接的出结果了!
,这样就可以直接的出结果了!