蓝桥杯第10天

快速幂

解题：掌握取模运算性质，通过快速倍增幂运算加快计算效率

import os
import sys

# 请在此输入您的代码

b,p,k = map(int,input().split())
def fastPow(a,n,mod):
  ans=1   # 返回的结果
  while n:  # 将n看成二进制数
    if n&1:  # 把n看成二进制数，逐个处理最后一位，判断是否为1
      ans = ans *a %mod  # 如果n的最后一位是1，这个地方需要乘
    a =a *a % mod  # 继续分解    a^0 a^2 a^4 a^8
    n>>=1      # 右移一位
  return ans

print(fastPow(b,p,k))

寻找素数

1不是素数，范围从[2--int(sqrt(x)+1)]内找

可以用itertools中的collections找排列

import itertools
import math

def is_prime(x):
    if x==1:  # 1不是素数
        return False
    for i in range(2,int(math.sqrt(x)+1)):  # 从2--int(sqrt(x)+1)
        if x%i==0:
            return False
    return True

n,k = map(int,input().split())
my_list = [int(x) for x in input().split()]
cnt = 0
for e in itertools.combinations(my_list,k):
    num=sum(e)
    if is_prime(num) :
        cnt+=1

print(cnt)

简单题，送分题，判断素数以及字符串统计

内置函数max，min，字符串函数 str.count()

import os
import sys

# 请在此输入您的代码
import math

word = input()
def is_primer(x):
  if x==1 or x==0:
    return False
  for i in range(2,int(1+math.sqrt(x))):
    if x %i==0:   return False
  return True

max_count = -1
min_count = 100
for i in word:
  # if word.count(i)>max_count:
  #   max_count=word.count(i)
  # if word.count(i)

字符串处理，判断个数

通过字典来判断有多少个数，但是有字典序问题，最好用列表来存储个数

dic = {}
# 通过80%，原因出在字典排序上
for i in input():
   dic[i]=dic.get(i,0)+1
a=sorted(dic.items(),key = lambda s:s[1])

# 方法一自定义排序规则
# 方法二排序后自己处理
val = a[-1][1]
my_list =[a[-1][0]]
i=-2
while 1:  # 将所有最大值加进列表处理字典序
 if a[i][1]==val:
    my_list.append(a[i][0]) 
    i-=1
 else:break
my_list.sort()
print(my_list[0])
print(val)



# s = input()
# n = [0]*256
# for ch in s:
#   n[ord(ch)]=n[ord(ch)]+1   # 转为ASCII码存储
# k = n.index(max(n))
# print(chr(k)) # 转为字符
# print(max(n))

送分题字符串，比较字符串大小，重在方法从左到右遍历，这个不能改变顺序

import os
import sys

# 请在此输入您的代码
# 这里要求原来顺序

s = list(input())
k = eval(input())
for _ in range(k):  # 从左到右遍历，左大就删除
  for i in range(len(s)-2):  # len-1 下标从1开始，即尾元素
    if s[i]>s[i+1]:
      del s[i]
      break  # 记得跳出循环，不然index错误

print(''.join(s))

送分题，将数字转为字符串排序来判断数字的性质

import os
import sys

# 请在此输入您的代码

n = int(input())
ans =0
for i in range(1,n+1):  # 1-n
  s=list(str(i))
  if sorted(s) == s:  
    ans+=1
print(ans)

中档难度，DFS搜索加上字符拼接，判断子集

def check(x,y):  # （drag,word）后，前
    flag =0
    for i in range(1,min(len(x),len(y))):  # 遍历查找是否有公共部分
        if x[-i:len(x)] ==y[:i]:
            flag = 1   # 找到公共部分
            break
    if flag==1: # 判断是否为子集
        if x in y or y in x:    return False
        else: return i
    else:
        return False

def dfs(drag,last):
    global ans
    ans = max(ans,len(drag))  # 更新最大值
    for i in range(n):  # 遍历找下一个
        if check(last,word[i]) !=False and vis[i]<2:  # 能够拼接同时没用到两次
            r = drag+word[i][check(last,word[i]):]  # 拼接
            vis[i]+=1
            dfs(r,word[i])  # DFS搜索下一个
            vis[i]-=1

n = int(input())
word =[]
for i in range(n):
    word.append(input())
first = input()
ans =0
for i in range(n):
    vis=[0]*n
    if word[i][0]==first:
        vis[i]+=1     # 每个最多只能用2次
        res = word[i]  # 记录上一个拼接的
        dfs(res,res)
print(ans)

平面切分问题

关键在于掌握关系：切分数=与原来存在直线的交点数+1

总结:每增加一条直线，平面分割的增加数量，等于“其与先前直线的交点数（不包括与已有交点重合的点）+1”。

import math
n = int(input())
line =[tuple(map(int,input().split(" "))) for i in range(n)]
#line2=[]
se = set(line) # 去重
##for x,y in line:
##    g = gcd(x,y)
##    line2.append((x//g,y//g))
# 不需要用gcd来处理
line = line(se)
ans = 2
for i in range(1,len(line)):
    a1,b1 = line[i]
    pos = set()
    for j in range(i):  #第i条直线与前面的直线的关系
        a2,b2 = line[j]
        if a1 ==a2 : continue   # 斜率相同，即直线平行
        # y = a1x+b1
        # y = a2x+b2
        x = (b1-b2)/(a1-a2)    # 计算两条直线的交点
        y = a1*x+b1
        pos.add((x,y))   # 存交刀集合，去重
    ans += len(pos)+1

print(ans)

三角形面积计算

注意面积为正，格式化输出方法

方法一

方法二

import os
import sys

# 请在此输入您的代码
n = int(input())
m=[0]
for i in range(3*n):
  m.append(tuple(map(float,input().split())))

for i in range(1,n+1):  # 得到两个向量
  x1=(m[3*i-1][0]-m[3*i][0],m[3*i-1][1]-m[3*i][1])
  x2=(m[3*i-2][0]-m[3*i][0],m[3*i-2][1]-m[3*i][1])
  s=(x1[0]*x2[1]-x1[1]*x2[0])/2
  if s<0:  # 注意面积为正
      s=-s
  print("{:.2f}".format(s))

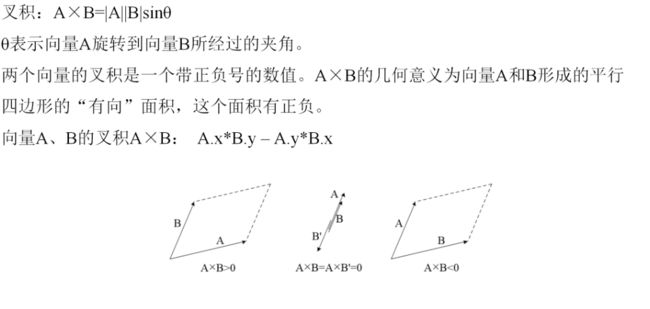
点积和叉积的应用

通过叉乘判断点与直线的关系

def Cross(x1,y1,x2,y2):
    return x1*y2-y1*x2   # 叉积
t = int(input())
for _ in range(t):
    ax,ay = map(float,input().split())
    bx,by = map(float,input().split())
    cx,cy = map(float,input().split())
    x1=ax-cx
    y1=ay-cy
    x2=bx-cy
    y2=by-cy
    s = Cross(x1,y1,x2,y2)/2  #用叉乘算面积
    if s>0:print('L')
    if s<0:print("R")
    if s==0 :print("IN")

判断点与线段关系

在上一题基础上判断是否在[ax,bx]区间即可

def Cross(x1,y1,x2,y2):
    return x1*y2-y1*x2   # 叉积
t = int(input())
for _ in range(t):
    ax,ay = map(float,input().split())
    bx,by = map(float,input().split())
    cx,cy = map(float,input().split())
    x1=ax-cx
    y1=ay-cy
    x2=bx-cy
    y2=by-cy
    s = Cross(x1,y1,x2,y2)/2  #用叉乘算面积
    if s==0 and ax<=cx<=bx:
      print("Yse")
    else:
      print("No")