算法设计与智能计算 || 专题四: 模型性能度量

模型性能度量

模型的性能度量有三种：损失函数、代价函数与目标函数。

• 损失函数（Loss Function）：是定义在单个样本上的，是指一个样本的误差，度量模型一次预测的好坏。是定义在单个训练样本上的，也就是就算一个样本的误差，比如我们想要分类，就是预测的类别和实际类别的区别，是一个样本的哦，用L表示。
• 代价函数（Cost Function）=成本函数=经验风险：是定义在整个训练集上的，是所有样本误差的平均，也就是所有损失函数值的平均，度量平均意义下模型预测的好坏。是定义在整个训练集上面的，也就是所有样本的误差的总和的平均，也就是损失函数的总和的平均，有没有这个平均其实不会影响最后的参数的求解结果。
• 目标函数（Object Function）=结构风险=经验风险+正则化项=代价函数+正则化项：是指最终需要优化的函数，一般指的是结构风险。

正则化项（regularizer）=惩罚项（penalty term）

1. 什么是损失函数？

损失函数是一种衡量模型与数据吻合程度的表达式。损失函数测量实际测量值和预测值之间差距的一种方式。损失函数的值越高预测就越错误，损失函数值越低则预测越接近真实值。对每个单独的观测(数据点)计算损失函数。将所有损失函数（loss function）的值取平均值的函数称为代价函数（cost function），更简单的理解就是损失函数是针对单个样本的，而代价函数是针对所有样本的。

由于损失函数测量的是预测值和实际值之间的差距，因此在训练模型时可以使用它们来指导模型的改进(通常的梯度下降法)。在构建模型的过程中，如果特征的权重发生了变化得到了更好或更差的预测，就需要利用损失函数来判断模型中特征的权重是否需要改变，以及改变的方向。

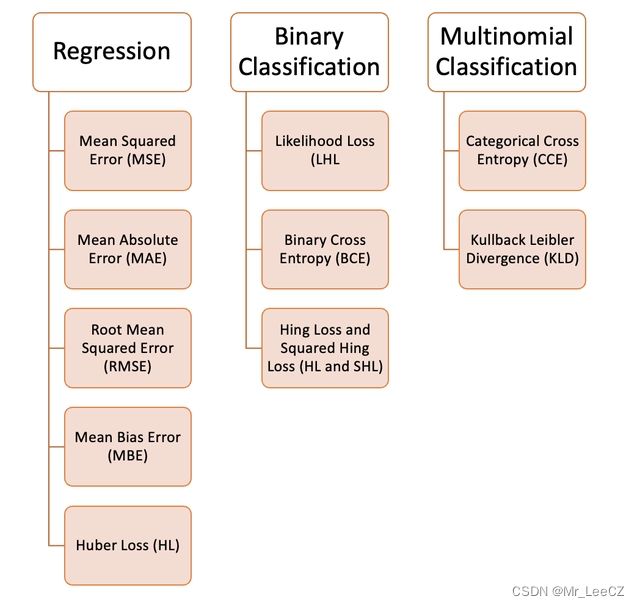
我们可以在机器学习中使用各种各样的损失函数，这取决于我们试图解决的问题的类型、数据质量和分布以及我们使用的算法，下图为我们整理的10个常见的损失函数：

1.1 回归问题

均方误差(MSE)

均方误差是指所有预测值和真实值之间的平方差，并将其平均值(Minimized Squared Eerror, MSE

损失函数：
$$Loss(\mathbf{w})=(y-\hat{y}(\mathbf{w}){)}^2$$

def MSE (y, y_predicted):
	sq_error = (y_predicted - y) ** 2
	sum_sq_error = np.sum(sq_error)
	mse = sum_sq_error/y.size
return mse

代价函数：
C o s t ( w ) = 1 N ∑ i = 1 N ( y i − y ^ i ( w ) ) 2 = 1 N ( ∑ i = 1 N ( y i − y ^ i ( w ) ) 2 ) 2 = 1 N ∥ y − y ^ ( w ) ∥ 2 2 Cost(\boldsymbol{w})=\frac{1}{N}\sum_{i=1}^N \Big(y_i-\hat{y}_i(\boldsymbol{w})\Big)^2=\frac{1}{N}\Bigg(\sqrt{\sum_{i=1}^N \Big(y_i-\hat{y}_i(\boldsymbol{w})\Big)^2}\Bigg)^2=\frac{1}{N}\Big\Vert\boldsymbol{y-\hat{y}(\boldsymbol{w})}\Big\Vert_2^2 Cost(w)=N1​i=1∑N​(yi​−y^​i​(w))2=N1​(i=1∑N​(yi​−y^​i​(w))2 ​)2=N1​ ​y−y^​(w) ​22​

目标函数
E ( w ) = 1 N ∑ i = 1 N ( y i − y ^ i ( w ) ) 2 = 1 N ( ∑ i = 1 N ( y i − y ^ i ( w ) ) 2 ) 2 = 1 N ∥ y − y ^ ( w ) ∥ 2 2 E(\boldsymbol{w})=\frac{1}{N}\sum_{i=1}^N \Big(y_i-\hat{y}_i(\boldsymbol{w})\Big)^2=\frac{1}{N}\Bigg(\sqrt{\sum_{i=1}^N \Big(y_i-\hat{y}_i(\boldsymbol{w})\Big)^2}\Bigg)^2=\frac{1}{N}\Big\Vert\boldsymbol{y-\hat{y}(\boldsymbol{w})}\Big\Vert_2^2 E(w)=N1​i=1∑N​(yi​−y^​i​(w))2=N1​(i=1∑N​(yi​−y^​i​(w))2 ​)2=N1​ ​y−y^​(w) ​22​
此函数为普通OLS回归的目标函数。

岭回归目标函数为
E ( w ) = 1 N ∥ y − y ^ ( w ) ∥ 2 2 + λ ⋅ ∥ w ∥ 2 2 E(\boldsymbol{w})=\frac{1}{N}\Big\Vert\boldsymbol{y-\hat{y}(\boldsymbol{w})}\Big\Vert_2^2+\lambda\cdot \Big\Vert\boldsymbol{w}\Big\Vert_2^2 E(w)=N1​ ​y−y^​(w) ​22​+λ⋅ ​w ​22​

Lasso 回归的目标函数为
E ( w ) = 1 N ∥ y − y ^ ( w ) ∥ 2 2 + λ ⋅ ∥ w ∥ 1 E(\boldsymbol{w})=\frac{1}{N}\Big\Vert\boldsymbol{y-\hat{y}(\boldsymbol{w})}\Big\Vert_2^2+\lambda\cdot \Big\Vert\boldsymbol{w}\Big\Vert_1 E(w)=N1​ ​y−y^​(w) ​22​+λ⋅ ​w ​1​

1.1.2 平均绝对误差(MAE)

作为预测值和真实值之间的绝对差的平均值来计算的。最小绝对值法(Minimized Absolute Eerror, MAE)

损失函数
L o s s ( w ) = ∣ y i − y ^ i ( w ) ∣ Loss(\boldsymbol{w})=\Big\vert y_i-\hat{y}_i(\boldsymbol{w})\Big\vert Loss(w)= ​yi​−y^​i​(w) ​

代价函数（目标函数）为：
L ( w ) = 1 N ∑ i = 1 N ∣ y i − y ^ i ( w ) ∣ = 1 N ∥ y − y ^ ( w ) ∥ 1 L(\boldsymbol{w})=\frac{1}{N}\sum_{i=1}^N \Big\vert y_i-\hat{y}_i(\boldsymbol{w})\Big\vert=\frac{1}{N}\Big\Vert\boldsymbol{y-\hat{y}(\boldsymbol{w})}\Big\Vert_1 L(w)=N1​i=1∑N​ ​yi​−y^​i​(w) ​=N1​ ​y−y^​(w) ​1​

当数据有异常值时，这是比均方误差更好的测量方法。

def MAE (y, y_predicted):
	error = y_predicted - y
	absolute_error = np.absolute(error)
	total_absolute_error = np.sum(absolute_error)
	mae = total_absolute_error/y.size
return mae

2.3 均方根误差(RMSE)

这个损失函数是均方误差的平方根。如果我们不想惩罚更大的错误，这是一个理想的方法。
其损失与目标函数为

L ( w ) = 1 N ∑ i = 1 N ( y i − y ^ i ( w ) ) 2 = 1 N ∥ y − y ^ ( w ) ∥ 2 2 L(\boldsymbol{w})=\sqrt{\frac{1}{N}\sum_{i=1}^N \Big(y_i-\hat{y}_i(\boldsymbol{w})\Big)^2}=\sqrt{\frac{1}{N}\Big\Vert\boldsymbol{y-\hat{y}(\boldsymbol{w})}\Big\Vert_2^2} L(w)=N1​i=1∑N​(yi​−y^​i​(w))2 ​=N1​ ​y−y^​(w) ​22​ ​

def RMSE(y, y_predicted):
	sq_error = (y_predicted - y) ** 2
	total_sq_error = np.sum(sq_error)
	mse = total_sq_error/y.size
	rmse = math.sqrt(mse)
return rmse

2.4 Huber损失

Huber损失函数结合了平均绝对误差(MAE)和均方误差(MSE)的优点。这是因为Hubber损失是一个有两个分支的函数。一个分支应用于符合期望值的MAE，另一个分支应用于异常值。Hubber Loss一般函数为:

Huber = { 1 2 ( y i − y ^ i ( w ) ) 2 ∣ y i − y ^ i ( w ) ∣ < δ δ ∣ y i − y ^ i ( w ) ∣ − 1 2 δ 2 Otherwise \text{Huber}=\left\{ \begin{array}{lcl} \frac{1}{2} \Big(y_i-\hat{y}_i(\boldsymbol{w})\Big)^2 & & \Big\vert y_i-\hat{y}_i(\boldsymbol{w})\Big\vert<\delta\\ \delta\Big\vert y_i-\hat{y}_i(\boldsymbol{w})\Big\vert -\frac{1}{2}\delta^2 & & \text{Otherwise} \end{array} \right. Huber=⎩ ⎨ ⎧​21​(yi​−y^​i​(w))2δ ​yi​−y^​i​(w) ​−21​δ2​​ ​yi​−y^​i​(w) ​<δOtherwise​

这里的

def hubber_loss (y, y_predicted, delta)
	delta = 1.35 * MAE
	y_size = y.size
	total_error = 0
	for i in range (y_size):
		erro = np.absolute(y_predicted[i] - y[i])
		if error < delta:
			hubber_error = (error * error) / 2
		else:
			hubber_error = (delta * error) / (0.5 * (delta * delta))
	total_error += hubber_error
	total_hubber_error = total_error/y.size
	return total_hubber_error

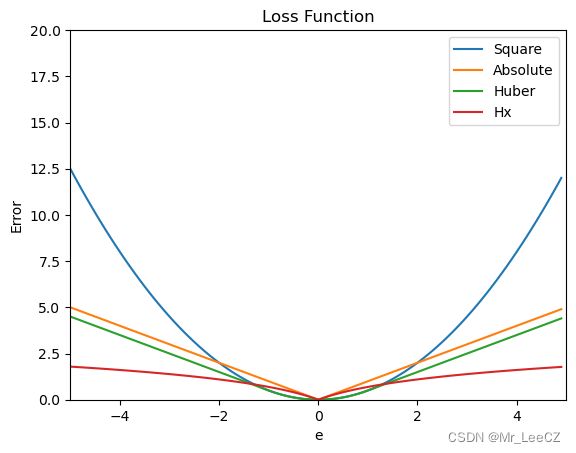
几种损失函数的比较

# huber 损失
def huber(e, delta):
    loss = np.where(np.abs(e) < delta , 0.5*(e**2), delta*np.abs(e) - 0.5*(delta**2))
    return loss


import numpy as np
import matplotlib.pyplot as plt

e = np.arange(-5,5,0.1)
z1 = 0.5*e**2
z2 = np.abs(e)
z3 = huber(e,1)
z4 = np.log(1+np.abs(e))

plt.plot(e,z1,label='Square')
plt.plot(e,z2,label='Absolute')
plt.plot(e,z3,label='Huber')
plt.plot(e,z4,label='Hx')
plt.title('Loss Function')
plt.axis([-5,5,0,20])
plt.legend()
plt.xlabel('e')
plt.ylabel('Error')
plt.show()

3. 二元分类

3.1 $0$-$1$ 损失

$$L(\mathbf{y},\hat{\mathbf{y}}(\mathbf{w}))=\{\begin{array}{r}0\mathbf{y}\ne \hat{\mathbf{y}}(\mathbf{w})\\ 1\mathbf{y}=\hat{\mathbf{y}}(\mathbf{w})\end{array}$$

3.2 最大似然损失(Likelihood Loss/LHL)

该损失函数主要用于二值分类问题。将每一个预测值的概率相乘,得到一个损失值，相关的代价函数是所有观测值的平均值。

假设有一个形状不规则的硬币，我们不知道它正面朝上的概率是多少，用 $\theta$ 表示，为模型的参数。想要求得这个模型参数 $\theta$ 是多少合适，就需要数据来进行估计。于是拿这枚硬币抛了10次，得到的数据为：“反正正正正反正正正反”。根据这个实验的结果我们就可以得到负对数似然函数为：

$$L(\theta )=-(log(1-\theta )+log(\theta )+log(\theta )+log(\theta )+log(\theta )+log(1-\theta )+log(\theta )+log(\theta )+log(\theta )+log(1-\theta ))=-(3log(1-\theta )+7log(\theta ))$$

让我们用以下二元分类的示例为例，其中类别为[0]或[1]。如果输出概率等于或大于0.5，则预测类为[1]，否则为[0]。输出概率的示例如下:
$[0.3,0.7,0.8,0.5,0.6,0.4]$
对应的预测类为:
$[0,1,1,1,1,0]$
而实际的类为：
$[0,1,1,0,1,0]$
现在将使用真实的类和输出概率来计算损失。如果真类是[1]，我们使用输出概率，如果真类是[0]，我们使用1-概率:
((1–0.3)+0.7+0.8+(1–0.5)+0.6+(1–0.4)) / 6 = 0.65
Python代码如下:

def LHL (y, y_predicted):
	likelihood_loss = (y * y_predicted) + ((1-y) * (y_predicted))
	total_likelihood_loss = np.sum(likelihood_loss)
	lhl = - total_likelihood_loss / y.size
	return lhl

3.3 二元交叉熵(BCE)

这个函数是对数的似然损失的修正。对数列的叠加可以惩罚那些非常自信但是却错误的预测。二元交叉熵损失函数的一般公式为:
$$y.log(p)+(1—y).log(1—p)$$
让我们继续使用上面例子的值：
输出概率= [0.3、0.7、0.8、0.5、0.6、0.4]
实际的类= [0，1，1，0，1，0]
$(0.log(0.3)+(1–0).log(1–0.3))=0.155$
$(1.log(0.7)+(1–1).log(0.3))=0.155$
$(1.log(0.8)+(1–1).log(0.2))=0.097$
$(0.log(0.5)+(1–0).log(1–0.5))=0.301$
$(1.log(0.6)+(1–1).log(0.4))=0.222$
$(0.log(0.4)+(1–0).log(1–0.4))=0.222$
那么代价函数的结果为：
$$(0.155+0.155+0.097+0.301+0.222+0.222)/6=0.192$$
Python的代码如下：

def BCE (y, y_predicted):
	ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted))
	total_ce = np.sum(ce_loss)
	bce = - total_ce/y.size
	return bce

3.4 Hinge Loss 和 Squared Hinge Loss (HL and SHL)

Hinge Loss 被翻译成铰链损失或者合页损失，这里还是以英文为准。
Hinge Loss主要用于支持向量机模型的评估。错误的预测和不太自信的正确预测都会受到惩罚。 所以一般损失函数是：
l(y) = max (0 , 1 — t . y)
这里的t是真实结果用[1]或[-1]表示。
使用Hinge Loss的类应该是[1]或-1。为了在Hinge loss函数中不被惩罚，一个观测不仅需要正确分类而且到超平面的距离应该大于margin(一个自信的正确预测)。如果我们想进一步惩罚更高的误差，我们可以用与MSE类似的方法平方Hinge损失,也就是Squared Hinge Loss。
如果你对SVM比较熟悉，应该还记得在SVM中，超平面的边缘（margin）越高，则某一预测就越有信心。如果这块不熟悉，则看看这个可视化的例子:

如果一个预测的结果是1.5，并且真正的类是[1]，损失将是0(零)，因为模型是高度自信的。
loss= Max (0,1 - 1* 1.5) = Max (0， -0.5) = 0

如果一个观测结果为0(0)，则表示该观测处于边界(超平面)，真实的类为[-1]。损失为1，模型既不正确也不错误，可信度很低。
loss = max (0 , 1–(-1) * 0) = max (0 , 1) = 1

如果一次观测结果为2，但分类错误(乘以[-1])，则距离为-2。损失是3(非常高)，因为我们的模型对错误的决策非常有信心（这个是绝不能容忍的）。
loss = max (0 , 1 — (-1) . 2) = max (0 , 1+2) = max (0 , 3) = 3
python代码如下：

#Hinge Loss
def Hinge (y, y_predicted):
	hinge_loss = np.sum(max(0 , 1 - (y_predicted * y)))
	return hinge_loss

#Squared Hinge Loss
def SqHinge (y, y_predicted):
	sq_hinge_loss = max (0 , 1 - (y_predicted * y)) ** 2
	total_sq_hinge_loss = np.sum(sq_hinge_loss)
	return total_sq_hinge_loss

4. 多分类

4.1 交叉熵（CE）

在多分类中，我们使用与二元交叉熵类似的公式，但有一个额外的步骤。首先需要计算每一对[y, y_predicted]的损失，一般公式为:

如果我们有三个类，其中单个[y, y_predicted]对的输出是:

这里实际的类3（也就是值=1的部分），我们的模型对真正的类是3的信任度是0.7。计算这损失如下:
Loss = 0 . log (0.1) + 0 . log (0.2) + 1 . log (0.7) = -0.155
为了得到代价函数的值，我们需要计算所有单个配对的损失，然后将它们相加最后乘以[-1/样本数量]。代价函数由下式给出:

使用上面的例子，如果我们的第二对:

Loss = 0 . log (0.4) + 1. log (0.4) + 0. log (0.2) = -0.40
那么成本函数计算如下:

使用Python的代码示例可以更容易理解:

def CCE (y, y_predicted):
	cce_class = y * (np.log(y_predicted))
	sum_totalpair_cce = np.sum(cce_class)
	cce = - sum_totalpair_cce / y.size
return cce

4.2 Kullback-Leibler 散度 (KLD)

又被简化称为KL散度，它类似于分类交叉熵，但考虑了观测值发生的概率。 如果我们的类不平衡，它特别有用。

def KL (y, y_predicted):
	kl = y * (np.log(y / y_predicted))
	total_kl = np.sum(kl)
	return total_kl

以上就是常见的10个损失函数，希望对你有所帮助.